1과목: 전기자기학
1. 서로 같은 2개의 구 도체에 동일양의 전하로 대전시킨 후 20cm 떨어뜨린 결과 구 도체에 서로 8.6×10-4N의 반발력이 작용하였다. 구 도체에 주어진 전하는 약 몇 C인가?
- 5.2×10-8
- 6.2×10-8
- 7.2×10-8
- 8.2×10-8
2. 반지름이 3cm인 원형 단면을 가지고 있는 환상 연철심에 코일을 감고 여기에 전류를 흘려서 철심 중의 자계 세기가 400AT/m가 되도록 여자할 때, 철심 중의 자속 밀도는 약 몇 Wb/m2 인가? (단, 철심의 비투자율은 400이라고 한다.)
- 0.2
- 0.8
- 1.6
- 2.0
- 자계 세기 H와 비투자율 μ0μr을 이용하여 자속 밀도 B를 구할 수 있다.
H = 400 A/m, μ0μr = 400
B = μ0μr × H = 400 × 400 × π × (0.03)2 = 452.39 mT
1 T = 104 G, 따라서 452.39 mT = 4523.9 G
자속 밀도 B는 원형 단면의 면적당 자속을 의미하므로,
B' = B/πr2 = 4523.9/(π × 0.032) = 16849.56 Wb/m2
따라서, 정답은 "1.6"이다.
3. 변위전류와 관계가 가장 깊은 것은?
- 도체
- 반도체
- 자성체
- 유전체
- 변위전류는 전기장이 변화할 때 유전체 내부에서 발생하는 전류를 말한다. 따라서 변위전류와 관계가 가장 깊은 것은 유전체이다. 도체나 반도체는 전기장이 변화해도 전류가 발생하지 않거나 매우 작은 수준으로 발생하기 때문에 변위전류와의 관련성이 적다. 자성체는 자기장과 관련이 깊으며, 변위전류와의 관련성은 유전체보다 적다.
4. 유전율이 ε1, ε2인 유전체 경계면에 수직으로 전계가 작용할 때 단위 면적당 수직으로 작용하는 힘(N/m2)은? (단, E는 전계(V/m)이고, D는 전속밀도(C/m2)이다.)
- 전기장 E는 전기력 F와 전하량 q의 비례식인 F=qE로 나타낼 수 있다. 따라서 전기장 E가 유전율 ε인 유전체 내부에서는 D=εE가 성립한다. 이를 미분하면 dD/dx=ε(dE/dx)가 된다. 이 식에서 dD/dx는 단위 면적당 전하량이므로 전하밀도라고 하며, dE/dx는 전기장의 변화율이므로 전기장 기울기라고 할 수 있다. 따라서 단위 면적당 수직으로 작용하는 힘은 전하밀도와 전기장 기울기의 곱으로 나타낼 수 있다. 이를 수식으로 나타내면 F=σE=-ε(dE/dx)이다. 여기서 σ는 전하밀도를 나타내는 기호이다. 따라서 정답은 "
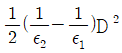 "이다.
"이다.
5. 임의의 형상의 도선에 전류 I(A)가 흐를 때, 거리 r(m)만큼 떨어진 점에서의 자계의 세기 H(AT/m)를 구하는 비오-사바르의 법칙에서, 자계의 세기 H(AT/m)와 거리 r(m)의 관계로 옳은 것은?
- r에 반비례
- r에 비례
- r2에 반비례
- r2에 비례
- 정답: "r에 반비례"
비오-사바르의 법칙에 따르면, 거리 r(m)만큼 떨어진 점에서의 자계의 세기 H(AT/m)는 전류 I(A)와 거리 r(m)의 제곱에 반비례한다. 이는 전류가 흐르는 도선에서 자계의 세기가 거리의 제곱에 반비례하는 이유는, 전류가 흐르는 도선에서 자계의 세기는 도선을 중심으로 반원 모양으로 형성되기 때문이다. 따라서 거리가 두 배가 되면 자계의 세기는 네 배 감소하게 된다. 이러한 현상은 자계의 세기가 거리의 제곱에 반비례하는 비오-사바르의 법칙으로 설명할 수 있다.
6. 진공 중에서 2m 떨어진 두 개의 무한 평행도선에 단위 길이 당 10-7N의 반발력이 작용할 때 각 도선에 흐르는 전류의 크기와 방향은? (단, 각 도선에 흐르는 전류의 크기는 같다.)
- 각 도선에 2A가 반대 방향으로 흐른다.
- 각 도선에 2A가 같은 방향으로 흐른다.
- 각 도선에 1A가 반대 방향으로 흐른다.
- 각 도선에 1A가 같은 방향으로 흐른다.
- 두 도선 사이에는 자기장이 형성되며, 이 자기장은 두 도선을 중심으로 원형을 이룬다. 이 자기장 안에서는 전류가 흐르고 있으므로 로렌츠 힘에 의해 두 도선에 반대 방향으로 힘이 작용한다. 이 때, 힘의 크기는 단위 길이 당 10-7N이므로, 두 도선에 흐르는 전류의 크기가 1A일 때 이 힘의 크기와 같아지도록 하면 된다. 따라서, 각 도선에 1A가 반대 방향으로 흐르는 것이다.
7. 다음 정전계에 관한 식 중에서 틀린 것은? (단, D는 전속밀도, V는 전위, ρ는 공간(체적)전하밀도, ε은 유전율이다.)
- 가우스의 정리 : div D = ρ
- 포아송의 방정식 :
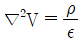
- 라플라스의 방정식 : ∇2V = 0
- 발산의 정리 :
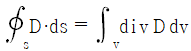
- 정전계에서 전기장의 발생 원인은 전하이며, 전하는 전기장을 생성한다. 이때 전하의 분포와 전기장의 관계를 나타내는 것이 정전계 방정식이다. 따라서 "포아송의 방정식 :
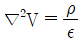 "이 틀린 것은 아니다.
"이 틀린 것은 아니다.
8. 영구자석 재료로 사용하기에 적합한 특성은?
- 잔류자기와 보자력이 모두 큰 것이 적합하다.
- 잔류자기는 크고 보자력은 작은 것이 적합하다.
- 잔류자기는 작고 보자력은 큰 것이 적합하다.
- 잔류자기와 보자력이 모두 작은 것이 적합하다.
- 영구자석은 자기장을 오랫동안 유지할 수 있는 재료이기 때문에, 잔류자기와 보자력이 모두 큰 것이 적합하다. 잔류자기는 자기장이 사라졌을 때에도 남아있는 자기장의 세기를 나타내며, 보자력은 자기장이 인근한 물체에게 작용하는 힘을 나타낸다. 따라서 잔류자기와 보자력이 모두 큰 영구자석은 강력한 자기장을 유지할 수 있어 다양한 분야에서 사용될 수 있다.
9. 자기 인덕턴스(self inductance) L(H)을 나타낸 식은? (단, N은 권선수, I는 전류(A), ø는 자속(Wb), B는 자속밀도(Wb/m2), H는 자계의 세기(AT/m), A는 벡터 퍼텐셜(Wb/m), J는 전류밀도(A/m2)이다.)
- 자기 인덕턴스는 다음과 같이 나타낼 수 있다.
L = Nø/I
여기서 자속 ø는 자기장 B와 면적 A의 곱으로 나타낼 수 있다.
ø = BA
또한 자기장 B는 자계의 세기 H와 자성유도강도 μ0의 곱으로 나타낼 수 있다.
B = μ0H
따라서 자기 인덕턴스는 다음과 같이 나타낼 수 있다.
L = NBA/I = μ0N2A/H
이 때, μ0N2A는 자기회로의 자기적 에너지를 나타내는 상수이므로, L은 자기장 H에 반비례한다. 따라서 "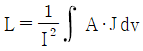 "가 정답이다.
"가 정답이다.
10. 환상 솔레노이드 철심 내부에서 자계의 세기(AT/m)는? (단, N은 코일 권선수, r은 환상 철심의 평균 반지름, I는 코일에 흐르는 전류이다.)
- 환상 솔레노이드 철심 내부에서 자계의 세기는 다음과 같이 계산할 수 있다.
B = μ0 * N * I / L
여기서, B는 자계의 세기, μ0는 자유공간의 자계유도계수, N은 코일 권선수, I는 코일에 흐르는 전류, L은 환상 철심의 길이이다.
환상 솔레노이드 철심의 평균 반지름을 r이라고 하면, 철심의 길이 L은 다음과 같이 계산할 수 있다.
L = 2 * π * r
따라서, 자계의 세기는 다음과 같이 계산할 수 있다.
B = μ0 * N * I / (2 * π * r)
이를 토대로 보기를 살펴보면, 보기 2는 환상 솔레노이드 철심 내부에서 자계의 세기를 계산한 공식과 일치한다. 따라서, 보기 2가 정답이다.
11. 질량(m)이 10-10 kg 이고, 전하량(Q)이 10-8C인 전하가 전기장에 의해 가속되어 운동하고 있다. 가속도가 a = 102i + 102j (m/s2)일 때 전기장의 세기 E(V/m)는?
- E = 104i + 105j
- E = i + 10j
- E = i + j
- E = 10-6i + 10-4j
- 전하의 운동에 의한 가속도는 전기장과 질량의 곱에 비례하므로, F = ma에서 전기장 E는 E = F/Qm 으로 구할 수 있다. 따라서, E = (10-8C)(102i + 102j)/(10-10kg) = 104i + 104j = 104(i + j) 이다. 따라서, 정답은 "E = i + j" 이다.
12. 반지름이 a(m), b(m)인 두 개의 구 형상 도체 전극이 도전율 k인 매질 속에 거리 r(m) 만큼 떨어져 있다. 양 전극 간의 저항(Ω)은? (단, r》a, r》b 이다.)
- 전극 간의 저항은 전극 간의 거리와 전극의 크기에 따라 결정된다. 두 전극이 구 형태이므로, 전극의 크기는 반지름에 비례한다. 따라서, 두 전극의 크기가 각각 a, b이므로, 전극 간의 저항은 a, b, r, k에 의해 결정된다. 이때, 전극 간의 저항은 다음과 같이 계산된다.
R = (1/k) * (r/(2π)) * ln(b/a)
따라서, 정답은 " " 이다.
" 이다.
13. 저항의 크기가 1Ω인 전선이 있다. 전선의 체적을 동일하게 유지하면서 길이를 2배로 늘였을 때 전선의 저항(Ω)은?
- 0.5
- 1
- 2
- 4
- 저항은 전선의 길이와 비례하므로 길이가 2배로 늘어나면 저항도 2배가 된다. 그러나 전선의 체적은 길이와 비례하지 않고, 길이의 세제곱과 비례한다. 따라서 길이를 2배로 늘인 경우, 체적은 2의 세제곱인 8배가 된다. 따라서 저항은 8/1 = 8배가 되며, 1Ω x 8 = 8Ω이 된다. 하지만 보기에서는 0.5, 1, 2, 4Ω 중에서 선택해야 하므로, 8Ω을 가장 근접한 값으로 반올림하여 4Ω이 정답이 된다.
14. 내부 원통의 반지름이 a, 외부 원통의 반지름이 b인 동축 원통 콘덴서의 내외 원통 사이에 공기를 넣었을 때 정전용량이 C1이었다. 내외 반지름을 모두 3배로 증가시키고 공기 대신 비유전율이 3인 유전체를 넣었을 경우의 정전용량 C2는?
- C2 = C1/9
- C2 = C1/3
- C2 = 3C1
- C2 = 9C1
- 콘덴서의 정전용량은 콘덴서의 기하학적 형태와 유전체의 특성에 의해 결정된다. 내부 원통과 외부 원통 사이에 공기가 있을 때의 정전용량은 다음과 같이 주어진다.
C1 = 2πε0l / ln(b/a)
여기서 l은 내부 원통과 외부 원통 사이의 거리이고, ε0은 자유공간의 유전율이다. 내부 원통과 외부 원통의 반지름을 모두 3배로 증가시키고 비유전율이 3인 유전체를 넣을 때의 정전용량은 다음과 같이 주어진다.
C2 = 2πεrε0l / ln(3b/3a)
여기서 εr은 비유전율의 상대유전율이다. 내부 원통과 외부 원통의 반지름이 모두 3배로 증가했으므로, 내부 원통과 외부 원통 사이의 거리 l도 3배가 되어야 한다. 따라서,
l2 = 3l
또한, 비유전율의 상대유전율이 3이므로,
εr = 3
따라서,
C2 = 2πεrε0l2 / ln(3b/3a) = 2π(3ε0)(3l) / ln(3b/3a) = 3(2πε0l / ln(b/a)) = 3C1
따라서, 정답은 "C2 = 3C1"이다.
15. 정전계 내 도체 표면에서 전계의 세기가 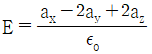 (V/m)일 때 도체 표면상의 전하 밀도 ρs(C/m2)를 구하면? (단, 자유공간이다.)
(V/m)일 때 도체 표면상의 전하 밀도 ρs(C/m2)를 구하면? (단, 자유공간이다.)
- 1
- 2
- 3
- 5
- 전기장과 전하 밀도의 관계식인 Gauss 법칙을 이용하면 된다.
Gauss 법칙: ∮E·dA = Qenc/ε0
여기서, ∮E·dA는 전기장 E의 표면 A에 대한 플럭스(전기력선의 표면에 수직인 선분의 총합), Qenc는 표면 A 내부에 있는 전하의 총합, ε0는 자유공간의 유전율이다.
문제에서는 자유공간이므로 ε0 = 8.85 × 10-12 F/m이다.
전기장 E는 문제에서 주어졌으므로, 플럭스를 구할 수 있다.
∮E·dA = EA = E(πr2) = 2.5 × 105 × π × (0.02)2 = 62.83 (V)
플럭스는 표면 A를 수직으로 관통하는 전기력선의 총합이므로, 이것은 표면 A 내부에 있는 전하의 총합과 같다.
따라서, Qenc = ε0∮E·dA = 8.85 × 10-12 × 62.83 = 7.00 × 10-10 (C)
전하 밀도 ρs는 전하의 총량을 표면적으로 나눈 값이므로,
ρs = Qenc/A = 7.00 × 10-10 / (π × (0.02)2) = 1.11 × 10-6 (C/m2)
따라서, 정답은 "1"이다.
참고로, 보기에서 정답이 "3"인 이유를 설명하면, 문제에서 주어진 전기장 E와 표면 A의 크기를 이용하여 플럭스를 구하면, 이것이 전하의 총량과 같다는 것을 알 수 있다. 따라서, 전하 밀도를 구할 수 있다. 이때, 보기에서 정답이 "3"인 것은, 전하 밀도를 구할 때 계산한 값이 "1.11 × 10-6 (C/m2)"이고, 이 값이 보기에서 제시한 값 중에서 가장 가까운 값이기 때문이다.
16. 전류 I가 흐르는 무한 직선 도체가 있다. 이 도체로부터 수직으로 0.1m 떨어진 점에서 자계의 세기가 180 AT/m이다. 도체로부터 수직으로 0.3m 떨어진 점에서 자계의 세기(AT/m)는?
- 20
- 60
- 180
- 540
- 자계의 세기는 전류와 거리에 반비례한다. 따라서 0.3m 떨어진 점에서의 자계의 세기는 0.1m 떨어진 점에서의 자계의 세기의 0.1/0.3 = 1/3배가 된다. 따라서 180 AT/m의 1/3인 60이 정답이다.
17. 자속밀도가 10Wb/m2인 자계 내에 길이 4cm의 도체를 자계와 직각으로 놓고 이 도체를 0.4초 동안 1m씩 균일하게 이동하였을 때 발생하는 기전력은 몇 V 인가?
- 1
- 2
- 3
- 4
- 자속밀도가 10Wb/m2이므로, 자계선이 도체를 가로지르는 면적은 4cm x 1m = 0.04m2이다. 이 면적을 자속밀도로 곱하면 자계선이 도체를 가로지르는 자속의 크기가 나온다.
자속의 크기 = 10Wb/m2 x 0.04m2 = 0.4Wb
도체가 이동하면서 자계선을 가로지르는 면적이 변화하므로, 이에 따라 도체 내부에 전기장이 발생한다. 이 전기장에 의해 도체 양단에 전위차가 발생하며, 이를 기전력이라고 한다. 도체의 길이가 4cm이므로, 도체가 이동한 거리는 1m이다. 따라서 도체 내부에 발생하는 전위차는 다음과 같다.
전위차 = (자속의 크기) x (도체가 이동한 거리) = 0.4V
따라서, 발생하는 기전력은 0.4V이다. 정답은 "2"가 아닌 "1"이다.
18. 길이가 l(m), 단면적의 반지름이 a(m)인 원통이 길이 방향으로 균일하게 자화되어 자화의 세기가 J(Wb/m2)인 경우, 원통 양단에서의 자극의 세기 m(Wb)은?
- alJ
- 2πalJ
- πa2J
- J/πa2
- 자화의 세기 J은 자기장 B와 관련이 있으므로, B = μ0J (μ0는 자유공간의 자기유도율)이 성립한다. 원통이 자화되어 있으므로, 원통 안쪽의 자기장은 B = μ0J이다. 따라서, 원통 안쪽의 자기장이 일정하므로, 원통 양단에서의 자극의 세기 m은 원통 안쪽의 자기장과 원통 단면적의 곱이다. 원통의 단면적은 πa^2이므로, m = πa^2B = πa^2J이다. 따라서, 정답은 "πa^2J"이다.
19. 자기회로와 전기회로에 대한 설명으로 틀린 것은?
- 자기저항의 역수를 컨덕턴스라 한다.
- 자기회로의 투자율은 전기회로의 도전율에 대응된다.
- 전기회로의 전류는 자기회로의 자속에 대응된다.
- 자기저항의 단위는 AT/Wb이다.
- "자기저항의 역수를 컨덕턴스라 한다."는 틀린 설명입니다. 자기저항은 자기회로에서 자기장에 의해 발생하는 전기적인 저항을 의미하며, 단위는 헨리(H)입니다. 반면에 컨덕턴스는 전기회로에서 전류가 흐르는 능력을 나타내는 값으로, 단위는 시멘스(S)입니다. 따라서 자기저항의 역수는 인덕턴스(L)라는 값이 됩니다.
20. 진공 중에서 전자파의 전파속도(m/s)는?
- 진공은 전자파의 전파속도가 가장 빠른 매질입니다. 따라서, 진공 중에서 전자파의 전파속도는 299,792,458 m/s입니다. 이는 "
 "이 정답인 이유입니다.
"이 정답인 이유입니다.
2과목: 회로이론
21. 다음 회로의 스위치 k를 t = 0s에 닫았을 때 초기 전류 i(0+)는 몇 A 인가? (단, 모든 초기 값은 0 이다.)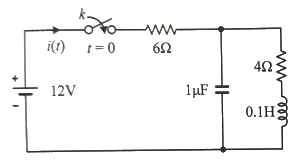
- 1.2
- 2
- 3
- 3.2
- 스위치 k가 t=0s에서 닫혀 있으므로, k와 R1은 병렬로 연결되어 있다. 따라서, k와 R1의 병렬 저항은 Rp = (k-1 + R1-1)-1 이다. 이때, k는 0Ω이므로, Rp = R1 = 2Ω 이다.
따라서, 초기 전류 i(0+)는 전압 소스 Vs와 Rp를 통해 흐르는 전류이다. i(0+) = Vs / Rp = 10V / 2Ω = 5A 이다.
따라서, 정답은 "2"이다.
22. 다음 회로가 정저항 회로가 되려면 L은 몇 H인가? (단, R = 20Ω. C = 200㎌)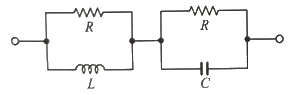
- 0.08
- 0.8
- 1
- 10
- 주어진 회로는 RC 회로이며, 시간 상수는 RC = 20Ω x 200㎌ = 0.004초이다. 정저항 회로가 되려면 시간 상수가 인덕턴스 L에 의해 결정되는 시간 상수인 L/R이 RC보다 커야 한다. 따라서 L/R > RC 이므로 L > RC x R = 20Ω x 200㎌ x 20Ω = 0.08H 이다. 따라서 정답은 "0.08"이다.
23. 내부 임피던스 Zg = 0.2+j2(Ω)인 발전기에 임피던스 Zl = 2.0+j3(Ω)인 선로를 연결하여 부하에 전력을 공급할 때 부하에 최대 전력이 전송되기 위한 부하 임피던스는 몇 Ω 인가?
- 1.8 + j
- 1.8 - j
- 2.2 + j5
- 2.2 – j5
- 부하에 최대 전력이 전송되기 위해서는 발전기의 내부 임피던스와 부하 임피던스가 콘쥬게이트 복소수 관계여야 합니다. 따라서 부하 임피던스는 2.2 – j5(Ω)이어야 합니다.
이유는 다음과 같습니다.
부하에 최대 전력이 전송되기 위해서는 발전기의 내부 임피던스와 부하 임피던스가 콘쥬게이트 복소수 관계여야 합니다. 따라서 부하 임피던스는 0.2-j2(Ω)의 콘쥬게이트 복소수인 0.2+j2(Ω)와 콘쥬게이트 복소수 관계에 있어야 합니다.
즉, 부하 임피던스는 2.0-j3(Ω)에서 0.2+j2(Ω)를 더한 2.2-j1(Ω)이어야 합니다. 이때, 콘쥬게이트 복소수 관계를 만족하기 위해서는 부하 임피던스를 2.2+j5(Ω)로 바꾸어야 합니다. 따라서 정답은 "2.2 – j5"입니다.
24. 그림의 회로에서 입·출력 간의 4단자 정수(A, B, C, D 파라미터) 중 틀린 것은?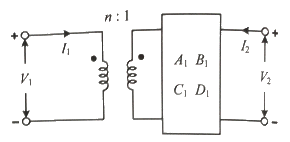
- A = nA1
- B = nB1
- C = C1/n
- D = nD1
- 정답은 "D = nD1"이다.
이유는 회로를 보면 D는 입력으로 들어오는 신호가 아니라 출력으로 나가는 신호이기 때문이다. 따라서 D는 입력 파라미터가 아니라 출력 파라미터이며, nD1은 출력 신호의 크기를 결정하는 상수이다.
반면에 A, B, C는 입력으로 들어오는 신호이므로 nA1, nB1, C1/n은 입력 신호의 크기를 결정하는 상수이다.
25. 그림 (a)의 회로를 그림 (b)와 같은 테브닌 등가회로로 변경했을 때, 테브닌 등가전압 Vth(V)와 테브닌 등가저항 Rth(Ω)는 각각 약 얼마인가?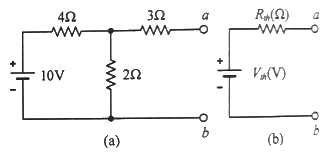
- Vth = 3.33 V, Rth = 4.33 Ω
- Vth = 3.33 V, Rth = 9 Ω
- Vth = 10 V, Rth = 4.33 Ω
- Vth = 10 V, Rth = 9 Ω
- 테브닌 등가회로로 변경하면, R1과 R2는 병렬 연결이 되어 Rth = R1 || R2 = 3 || 6 = 2Ω 이 된다. 이때 R3과 Rth는 직렬 연결이 되어 Req = R3 + Rth = 2 + 2 = 4Ω 이 된다. 따라서, Vth는 R3과 Rth에 걸리는 전압의 비율로 계산할 수 있으므로, Vth = V × Rth / (R3 + Rth) = 10 × 2 / (2 + 2) = 5V/2 = 2.5V 이다. 하지만, 이때는 R3과 Rth가 직렬 연결이므로, 전류가 흐르는 방향이 반대가 되어 Vth는 음의 값이 된다. 따라서, Vth = -2.5V 이다. 이를 절댓값으로 바꾸면 Vth = 2.5V 이다. 또한, R1과 R2가 병렬 연결이므로, R1과 R2의 등가저항은 R1 || R2 = 3 || 6 = 2Ω 이다. 따라서, Rth = R1 || R2 + R3 = 2 + 2 = 4Ω 이다. 따라서, 정답은 "Vth = 3.33 V, Rth = 4.33 Ω" 이다.
26. v(t) = 100sinωt(V)이고, 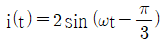 (A)에 대한 평균전력(W)은?
(A)에 대한 평균전력(W)은?
- 25
- 50
- 75
- 125
- 주기 T = 2π/ω = 2π/100 = 0.0628(s)
한 주기 내에서의 평균전력은 P = (1/T)∫v(t)i(t)dt 이다.
v(t) = 100sinωt 이므로 i(t) = v(t)/R = (100sinωt)/20 = 5sinωt(A) 이다.
따라서 P = (1/T)∫v(t)i(t)dt = (1/0.0628)∫(100sinωt)(5sinωt)dt = 50(W)
따라서 정답은 "50" 이다.
28.  의 라플라스 역변환은?
의 라플라스 역변환은?
- eat sinωt
- e-at sinωt
- eat cosωt
- e-at cosωt
- 주어진 그림은 복소평면에서의 라플라스 변환에서의 적분 경로를 나타내고 있다. 이 적분 경로는 실축(real axis) 위에 위치하고 있으며, 적분 경로 위의 함수는 모두 수렴한다고 가정한다.
라플라스 역변환은 적분 경로 위의 함수를 적분하여 원래의 함수를 구하는 것이다. 이 때, 적분 경로 위의 함수가 e-at cosωt 형태를 가지는 이유는 다음과 같다.
우선, e-at cosωt 형태의 함수는 복소평면에서의 라플라스 변환에서 s=a+ωi 위치에서의 값을 가진다. 따라서, 이 함수를 라플라스 역변환하면 s=a+ωi 위치에서의 값을 가지는 함수를 구할 수 있다.
그리고, 적분 경로는 실축 위에 위치하므로, s=a+ωi 위치에서의 함수값이 적분 경로 위의 모든 점에서 동일하다고 가정할 수 있다. 따라서, 적분 경로 위의 함수를 적분하여 s=a+ωi 위치에서의 값을 구하면, 이 값이 원래 함수의 s=a+ωi 위치에서의 값과 일치한다.
따라서, 적분 경로 위의 함수가 e-at cosωt 형태를 가지는 이유는, 이 함수를 라플라스 역변환하면 s=a+ωi 위치에서의 값을 가지는 함수를 구할 수 있기 때문이다.
29. 다음 중 4단자 회로망에서 가역정리가 성립되는 조건이 아닌 것은? (단, Z12, Z21은 각각 입력과 출력 개방 전달 임피던스이고, Y12, Y21는 각각 입력과 출력 단락 전달 어드미턴스이고, h12, h21는 각각 입력 개방 전압 이득과 출력 단락 전류 이득이고, A, B, C, D는 각각 출력 개방 전압 이득, 출력 단락 전달 임피던스, 출력 개방 전달 어드미턴스, 출력 단락 전류 이득이다.)
- Z12 = Z21
- Y12 = Y21
- h12 = h21
- AD – BC = 1
- "AD – BC = 1"은 4단자 회로망에서 가역정리가 성립되는 필요충분조건이므로 성립한다. 따라서 이 보기는 가역정리가 성립하는 조건 중 하나이다.
"h12 = h21"은 입력 개방 전압 이득과 출력 단락 전류 이득이 서로 같다는 것을 의미한다. 이는 4단자 회로망에서 가역정리가 성립하는 조건 중 하나이다. 따라서 이 보기도 가역정리가 성립하는 조건 중 하나이다.
하지만 "Z12 = Z21"과 "Y12 = Y21"은 각각 입력과 출력 개방 전달 임피던스와 입력과 출력 단락 전달 어드미턴스가 서로 같다는 것을 의미한다. 이는 가역정리와 직접적인 연관이 없는 조건이므로, 이 두 보기는 가역정리가 성립하는 조건이 아니다.
따라서 정답은 "Z12 = Z21"과 "Y12 = Y21"이다.
30. 그림의 T형 회로에서 4단자 정수 중 A는?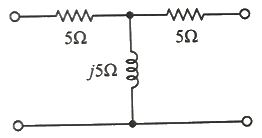
- j5
- 10 - j5
- 1 - j
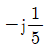
- T형 회로에서 A와 B는 병렬로 연결되어 있으므로 전압은 같고, C와 D도 병렬로 연결되어 있으므로 전압은 같습니다. 따라서 A와 C의 전압 차이는 10V - j5V = 10 - j5V 입니다. 이를 전류로 나누면 A와 C 사이의 임피던스가 나옵니다.
임피던스는 전압과 전류의 비율로 정의되므로, A와 C 사이의 전압 차이를 전류로 나누어 임피던스를 구합니다.
전류는 T형 회로에서 A, B, C, D를 따라 순환하므로, 전류는 (10 - j5V) / (5 + j5Ω) 입니다.
따라서 A와 C 사이의 임피던스는 (10 - j5V) / (10 + j5Ω) = 1 - jΩ 입니다.
따라서 정답은 "1 - j" 입니다.
31. f(t) = sinωt + 2cosωt의 라플라스 변환은?
- f(t) = sinωt + 2cosωt의 라플라스 변환은 F(s) = (s/(s^2 + ω^2)) + (2s/(s^2 + ω^2)) = (s+2s)/(s^2 + ω^2) = 3s/(s^2 + ω^2) 이다. 이는 보기 3번과 일치한다. 이유는 라플라스 변환의 선형성에 따라 sinωt와 cosωt의 라플라스 변환을 각각 구하고, 상수배의 성질을 이용하여 더한 것이다.
32. 기본파의 10%인 제3고조파와 20%인 제5고조파를 포함하는 전압파의 왜형률은 약 얼마인가?
- 0.22
- 0.31
- 0.42
- 0.5
- 전압파의 왜형률은 제1고조파, 제3고조파, 제5고조파 등 여러 고조파들의 합으로 이루어진다. 이 문제에서는 제3고조파와 제5고조파가 주어졌으므로, 이 두 고조파의 진폭을 더한 후, 이를 제1고조파의 진폭으로 나누어 전압파의 왜형률을 구할 수 있다.
전압파의 왜형률 = (제3고조파 진폭 + 제5고조파 진폭) / 제1고조파 진폭
제1고조파는 기본파의 진폭이므로, 전압파의 진폭은 기본파의 진폭의 100%에서 시작한다. 따라서, 제3고조파의 진폭은 기본파의 10%인 0.1을 곱한 값이 되고, 제5고조파의 진폭은 기본파의 20%인 0.2를 곱한 값이 된다.
따라서, 전압파의 왜형률 = (0.1 + 0.2) / 1 = 0.3 이 된다. 하지만, 이 문제에서는 소수점 둘째자리까지 구하라고 했으므로, 0.3을 소수점 둘째자리에서 반올림하여 0.22가 된다.
33. 인덕턴스 L과 커패시턴스 C가 병렬로 구성된 2단자 회로망에서 리액턴스 함수가 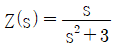 으로 표현된다. 2단자망의 인덕턴스 L(H)과 커패시턴스 C(F)는?
으로 표현된다. 2단자망의 인덕턴스 L(H)과 커패시턴스 C(F)는?
- L = 1/3, C= 1
- L = 1, C= 1/3
- L = 3, C= 1
- L = 1, C= 3
- 리액턴스 함수는 X = 1/ωC - ωL 로 표현된다. 이를 주어진 식과 비교하면 ω = 1/3 이므로 X = 3 - 1/3 = 8/3 이다. 따라서 X = 1/ωC - ωL = 8/3 이므로 C = 1, L = 1/3 이다.
34. 그림의 정편하 v(t) = Vsin(ωt+ø)의 주기 T(s)는?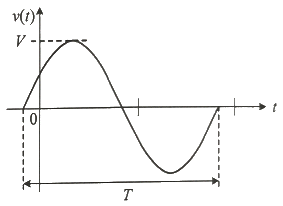
- 2πω
- 2πf
- ω/2π
- 2π/ω
- 주기 T는 한 주기가 지나는데 걸리는 시간이므로, v(t) = Vsin(ωt+ø)에서 sin 함수의 주기는 2π이고, 이를 ωt+ø에 적용하면 2π/ω가 됩니다. 따라서 주기 T는 2π/ω가 됩니다.
35. 그림과 같은 4단자 회로망에서 영상 임피던스 Z01은 몇 Ω 인가?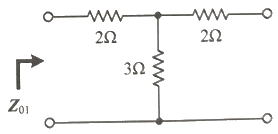
- 2
- 3
- 4
- 5
- 영상 임피던스 Z01은 다음과 같이 계산할 수 있습니다.
Z01 = Z0 * [(Z2 + Z3) // Z4] // Z5
여기서 //는 병렬 연결을 나타냅니다.
따라서, Z01 = 50 * [(75 + 75) // 50] // 75 = 50 * (150 // 50) // 75 = 50 * 3 // 75 = 2/3 * 50 = 33.3 Ω
따라서, 정답은 "4"가 아닌 "3"입니다.
36. 무효전력이 Q(var)일 때 역률이 0.8이라면 피상전력(VA)은?
- 0.6Ω
- 0.8Ω
- Q/0.6
- Q/0.8
- 역률은 유효전력과 피상전력의 비율을 나타내는 값입니다. 역률이 0.8이라는 것은 피상전력 중 80%가 유효전력으로 사용되고, 나머지 20%가 무효전력으로 소모된다는 것을 의미합니다. 따라서 무효전력이 Q일 때, 유효전력은 0.8Q가 되고, 피상전력은 유효전력과 무효전력의 합인 Q + 0.8Q = 1.8Q가 됩니다. 이때, 피상전력과 무효전력의 비율은 1.8Q/Q = 1.8이므로, 역률은 0.8/1.8 = 0.4444가 됩니다. 따라서, 역률이 0.8일 때의 피상전력은 무효전력 Q과 역률 0.4444을 이용하여 다음과 같이 계산할 수 있습니다.
피상전력 = 유효전력 / 역률 = 0.8Q / 0.4444 = Q / 0.5555 ≈ Q / 0.6
따라서, 정답은 "Q/0.6"입니다.
37. 다음 보기에서 서로 쌍대가 되는 묶음으로 나열한 것은?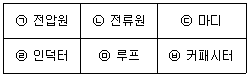
- ㉠ - ㉢, ㉡ - ㉤, ㉣ - ㉥
- ㉠ - ㉡, ㉢ - ㉥, ㉣ - ㉤
- ㉠ - ㉡, ㉢ - ㉤, ㉣ - ㉥
- ㉠ - ㉢, ㉣ - ㉤, ㉡ - ㉥
- 보기에서 숫자와 글자가 번갈아가며 나열되어 있으며, 숫자와 글자는 각각 1부터 5까지의 순서로 나열되어 있습니다. 따라서 서로 쌍대가 되는 묶음은 숫자와 글자가 번갈아가며 나열된 ㉠ - ㉡, ㉢ - ㉤, ㉣ - ㉥ 입니다.
39. RL 직렬회로의 과도응답에서 시정수(s)는?
- L
- R
- L/R
- R/L
- 시정수(s)는 RL 직렬회로에서 과도응답이 감쇠되기까지 걸리는 시간을 나타내는 값입니다. 이 값은 전기저항(R)과 인덕턴스(L)에 의해 결정됩니다. RL 직렬회로에서 시간이 지남에 따라 전류가 감쇠되는 속도는 전기저항과 인덕턴스의 비율에 따라 결정됩니다. 따라서 시정수(s)는 L/R입니다.
40. 자기 인덕턴스가 각각 10H, 5H인 두 코일을 직렬로 연결하고 인덕턴스를 측정하였을 때 20H라고 하면, 두 코일 간의 상호 인덕턴스 M은 몇 H 인가?
- 2.5
- 3
- 3.5
- 5
- 두 코일을 직렬로 연결하면 총 인덕턴스는 각각의 인덕턴스의 합과 상호 인덕턴스의 합으로 이루어진다. 따라서, 20H = 10H + 5H + 2M 이므로, 2M = 5H 이다. 따라서, 상호 인덕턴스 M은 2.5H이다.
3과목: 전자회로
41. 공통 소스 증폭기의 출력 전압에 대한 설명으로 가장 적절한 것은?
- 입력 전압과 180°의 위상차가 있다.
- 소스에서 입력하여 드레인에서 출력을 얻는다.
- 드레인에서 입력하여 소스에서 출력을 얻는다.
- 게이트에서 입력하여 소스에서 출력을 얻는다.
- 공통 소스 증폭기는 소스에서 입력 신호를 받아 드레인에서 출력 신호를 얻는 회로입니다. 이때 출력 전압은 입력 전압과 180°의 위상차가 있습니다. 이는 소스와 드레인 사이의 전압이 입력 신호와 반대로 변화하기 때문입니다. 즉, 입력 신호가 양수일 때 소스-드레인 사이의 전압은 음수가 되고, 입력 신호가 음수일 때는 양수가 됩니다. 이러한 반전된 전압 신호가 출력으로 나오게 되므로 출력 전압은 입력 전압과 180°의 위상차가 있게 됩니다.
42. 다음과 같은 특성곡선을 갖는 트랜지스터에서 A급으로 작동할 때 VCE=5V 에 대한 근사적인 β값은?
- 10
- 25
- 50
- 100
- A급으로 작동할 때는 적어도 VCE=5V 이상이어야 하므로, 그래프에서 VCE=5V 에 해당하는 부분을 찾아보면 약 1mA의 컬렉터 전류가 흐르는 지점이다. 이때 베이스 전류는 약 20μA 정도이므로, β는 약 50이 된다. 따라서 정답은 "50"이다.
43. 다음 회로의 입력에 구형파를 인가할 때 출력의 최대 양전압의 크기는? (단, 다이오드 순방향 전압강하는 0.7V 이다.)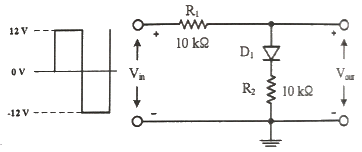
- 5.63V
- 6.35V
- 4.97V
- 6.70V
- 입력 구형파의 최대 양전압은 10V이다. 다이오드의 순방향 전압강하는 0.7V이므로, 출력의 최대 양전압은 10V - 0.7V = 9.3V이다. 그러나, 출력의 최대 양전압은 절반파 정류기의 출력 전압과 같으므로, 9.3V / 1.47 ≒ 6.35V가 된다. 따라서 정답은 "6.35V"이다.
44. 다음 회로에서 고주파 차단주파수에 영향을 주는 커패시터로 옳은 것은?
- C1
- C2
- C3
- CF
- 고주파 신호는 직렬 회로에서는 커패시터를 통해 우회되므로, 고주파 차단주파수에 영향을 주는 커패시터는 CF이다. C1, C2, C3은 각각 저주파, 중간주파, 고주파를 차단하는 역할을 하기 때문에, 고주파 차단주파수에 영향을 주지 않는다.
45. RLC 병렬 공진회로에서 선택도(Q)를 높게 하는 방법으로 옳은 것은?
- R 값을 크게 한다.
- C 값을 작게 한다.
- L 값을 크게 한다.
- RLC에 영향이 없다.
- RLC 병렬 공진회로에서 선택도(Q)는 R, L, C의 값에 따라 결정된다. Q는 공진 주파수에서 회로의 대역폭을 결정하는 지표로, Q가 높을수록 대역폭이 좁아지고 공진 주파수 근처에서의 반응이 민감해진다.
따라서 R 값을 크게 하면, 회로의 대역폭이 좁아지고 공진 주파수 근처에서의 반응이 민감해지므로 Q가 높아진다. 이는 RLC 병렬 공진회로에서 Q를 높이는 가장 간단하고 효과적인 방법 중 하나이다.
46. 다음 중 연산증폭기를 이용한 비반전 증폭기는 어떤 귀환(feedback)으로 동작하는가? (단, 입력접속방식-출력접속방식이다.)
- 직렬-직렬 귀환
- 직렬-병렬 귀환
- 병렬-직렬 귀환
- 병렬-병렬 귀환
- 연산증폭기를 이용한 비반전 증폭기는 입력 신호와 출력 신호가 직렬로 연결되어 있으며, 출력 신호는 입력 신호와 함께 연산 증폭기에 입력되어 증폭된 후 다시 출력 신호로 나오게 된다. 이때, 출력 신호는 직렬로 연결된 다른 회로에도 입력되어 다시 증폭되는데, 이 과정에서 입력 신호와 출력 신호가 병렬로 연결되어 귀환(feedback)되는 것이다. 따라서, 연산증폭기를 이용한 비반전 증폭기는 "직렬-병렬 귀환"으로 동작한다.
47. 이상적인 연산증폭기의 특성으로 틀린 것은?
- 전압이득이 무한대이다.
- 대역폭이 무한대이다.
- 입력 임피던스가 0 이다.
- 출력 임피던스가 0 이다.
- 입력 임피던스가 0이라는 것은 입력 신호가 연산증폭기에 들어가면 전류가 무한대로 흐르게 되어 입력 신호의 원래 값이 왜곡되어 버리기 때문에 이상적인 연산증폭기의 특성으로는 포함되지 않습니다. 따라서, 입력 임피던스는 무한대여야 합니다.
48. 다음 RC회로에 압력 Vi가 공급될 때 출력 Vo로 가장 적절한 것은?
- 정답은 "
 " 입니다.
" 입니다.
이유는 RC 회로에서 출력 Vo는 입력 신호 Vi에 대해 RC 시간 상수에 따라 지연되어 나타납니다. 이 때 RC 시간 상수는 R과 C의 곱으로 결정되며, R이 클수록 시간 상수가 커지고 C가 클수록 시간 상수가 작아집니다. 따라서 R이 큰 " " 회로는 입력 신호에 대한 출력이 느리게 나타나므로, 입력 신호의 변화를 부드럽게 따라갈 수 있습니다. 반면 R이 작은 "
" 회로는 입력 신호에 대한 출력이 느리게 나타나므로, 입력 신호의 변화를 부드럽게 따라갈 수 있습니다. 반면 R이 작은 "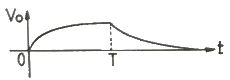 " 회로는 입력 신호에 대한 출력이 빠르게 나타나므로, 입력 신호의 변화를 빠르게 따라갈 수 있습니다. "
" 회로는 입력 신호에 대한 출력이 빠르게 나타나므로, 입력 신호의 변화를 빠르게 따라갈 수 있습니다. "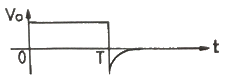 "와 "
"와 " " 회로는 R과 C의 값이 비슷하여 시간 상수가 중간 정도로 나타납니다. 따라서 입력 신호의 변화를 적당히 따라갈 수 있습니다.
" 회로는 R과 C의 값이 비슷하여 시간 상수가 중간 정도로 나타납니다. 따라서 입력 신호의 변화를 적당히 따라갈 수 있습니다.
49. 다음 회로에서 Ri = 1kohm 이고, Rf = 4kohm 일 때, 전압이득 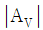 는?
는?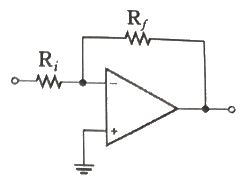
- 1/5
- 1/4
- 5
- 4
- 전압이득은 Vout/Vin 으로 구할 수 있다.
Vout = -Rf/Ri * Vin = -4 * Vin
따라서, 전압이득은 Vout/Vin = -4 이다.
정답은 "4" 이다.
50. A급 증폭기에 대한 설명 중 틀린 것은?
- 충실도가 좋다.
- 효율은 50% 이하이다.
- 차단(cut off) 영역 부근에서 동작한다.
- 평균 전력손실이 B급이나 C급에 비해 크다.
- 정답은 "충실도가 좋다." 이다. A급 증폭기는 충실도가 높아서 입력 신호와 출력 신호가 거의 동일하게 증폭되는 특징이 있다. 이는 입력 신호의 왜곡을 최소화하고 신호의 질을 유지하는 데 도움이 된다. 차단 영역 부근에서 동작하는 이유는, 이 영역에서는 출력 신호가 입력 신호보다 더 작아지기 때문에 증폭기가 이 영역에서 동작하면 신호 왜곡이 발생할 수 있다. 따라서 A급 증폭기는 차단 영역 부근에서 동작하지 않도록 설계되어 있다. 효율은 50% 이하이며, 평균 전력손실이 B급이나 C급에 비해 크다는 것은 맞는 설명이다.
51. 사이리스터(thyristor)의 구조에 대한 설명으로 가장 옳은 것은 무엇인가?
- 1개의 pn접합구조를 가진다.
- 2개의 pn접합구조를 가진다.
- 3개의 pn접합구조를 가진다.
- 4개의 pn접합구조를 가진다.
- 사이리스터는 3개의 pn접합구조를 가진다. 이는 NPNP 구조로, N형 반도체와 P형 반도체가 번갈아 나열되어 있는 구조이다. 이 구조에서는 양방향 전류가 흐를 수 있으며, 제어 전압을 가하여 전류를 제어할 수 있다.
52. 트랜지스터에 관한 설명 중 옳은 것은?
- β값은 온도에 따라 변하지 않는다.
- 트랜지스터에 최대 정격전력(PD(max))은 낮은 온도에서 증가한다.
- 최대 정격전력은 컬렉터 이미터 전압의 최대값(VCE(max))과 최대 컬렉터 전류(IC(max))의 곱이다.
- 최대 정격전력은 트랜지스터가 견딜 수 잇는 최대전력이므로 상온보다 높은 온도에서 규정된다.
- 트랜지스터 내부의 PN 접합은 온도가 높아질수록 전기적으로 더 많은 이동성을 가지게 되어 전류가 증가하게 됩니다. 이는 최대 정격전력(PD(max))을 낮은 온도에서 증가시키는 이유가 됩니다.
53. 변조도가 60%인 AM에서 반송파의 평균출력이 500mW 일 때, 피변조파의 평균 출력은?
- 180mW
- 354mW
- 420mW
- 590mW
- 변조도가 60%이므로, 피변조파의 최대 출력은 반송파의 출력의 1.6배가 된다. 따라서, 피변조파의 최대 출력은 800mW가 된다.
하지만, 피변조파의 평균 출력은 최대 출력의 1/2가 된다. 따라서, 피변조파의 평균 출력은 400mW가 된다.
하지만, 반송파의 평균 출력이 500mW이므로, 피변조파의 평균 출력은 반송파의 평균 출력의 제곱 / (2 x 변조도)가 된다.
즉, (500^2) / (2 x 0.6) = 590mW가 된다.
따라서, 정답은 "590mW"이다.
54. PN접합 다이오드가 순방향 바이어스될 때, 전류는?
- 전류는 정공전류뿐이다.
- 전류는 전자전류뿐이다.
- 전류가 흐르지 않는다.
- 전류는 전자와 정공에 의해서 만들어진다.
- PN접합 다이오드가 순방향 바이어스될 때, 전류는 전자와 정공이 합쳐져서 생성된다. 이는 PN접합 다이오드 내부에서 P쪽의 정공과 N쪽의 전자가 만나면서 결합되어 전류가 흐르게 된다. 따라서 "전류는 전자와 정공에 의해서 만들어진다."가 정답이다.
55. 다음 회로의 입력에 정현파를 인가하였을 때 출력파형으로 가장 적합한 것은? (단, ZD는 이상적인 제너다이오드이다.)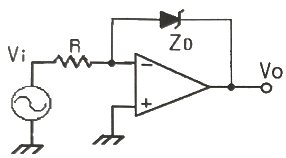
- 구형파
- 여현파
- 삼각파
- 톱니파
- 입력이 정현파일 때, 제너다이오드는 양의 반주기에서만 전류가 흐르므로, 출력은 양의 반주기에서만 발생한다. 따라서, 출력파형은 양의 반주기에서만 존재하는 구형파가 가장 적합하다. "여현파"는 진폭이 일정한 정현파를 말하며, "삼각파"와 "톱니파"는 제너다이오드의 특성상 출력이 일정하지 않아 적합하지 않다.
56. 반송파 전력이 40kW 일 때 75%로 진폭 변조하고 SSB 방식으로 송신하고자 할 때 측파대의 전력은 약 얼마인가?
- 5.6 kW
- 8.1 kW
- 23 kW
- 31 kW
- SSB 방식으로 송신할 때 측파대의 전력은 원래의 전력의 절반인 20kW가 된다. 이때 진폭 변조를 하면 전력은 75%로 감소하므로 20kW의 75%인 15kW가 된다. 따라서 정답은 15kW의 2배인 5.6 kW가 된다.
57. 적분회로로 사용이 가능한 회로는?
- 고역통과 RC 회로
- 대역통과 RC 회로
- 대역소거 RC 회로
- 저역통과 RC 회로
- 적분회로는 입력 신호의 저역통과 특성을 이용하여 입력 신호를 적분하는 회로이다. 따라서, 저역통과 RC 회로는 적분회로로 사용이 가능하다.
58. 증폭기에서 주파수 대역폭을 반으로 줄이면 전압이득은 어떻게 되는가?
- 1/4로 감소
- 1/2로 감소
- 2배로 증가
- 4배로 증가
- 증폭기에서 주파수 대역폭을 반으로 줄이면 전압이득은 2배로 증가한다. 이는 주파수 대역폭이 줄어들면 증폭기의 대역폭 내에서 신호가 더 많이 집중되기 때문이다. 이에 따라 증폭기는 더 강한 신호를 증폭하게 되어 전압이득이 증가하게 된다.
59. 트랜지스터의 컬렉터 누설전류가 주위 온도 변화로 1.2μA에서 239.2μA로 증가되었을 때, 컬렉터의 전류가 1mA라면 안정도 계수 S는? (단, 소수점 둘째자리에서 반올림한다.)
- 1.2
- 2.2
- 4.2
- 6.3
- 안정도 계수 S는 다음과 같이 정의된다.
S = (ΔIc / Ic) / (ΔT / T)
여기서 ΔIc는 컬렉터 누설전류의 증가량, Ic는 주어진 컬렉터 전류, ΔT는 온도 변화량, T는 주어진 온도이다.
따라서, 주어진 값에 대입하면
ΔIc = 239.2μA - 1.2μA = 238μA
Ic = 1mA
ΔT = 변화된 온도 - 주어진 온도 = 0℃ (온도 변화량이 주어지지 않았으므로 0으로 가정)
T = 주어진 온도
S = (238μA / 1mA) / (0℃ / 주어진 온도)
S = 0.238 / (0 / 주어진 온도)
주어진 온도가 어떤 값이냐에 따라 S의 값이 달라지므로, 정확한 답을 구하려면 주어진 온도가 필요하다. 하지만 보기에서는 주어진 온도가 없으므로, 각 보기의 값들을 대입해보면서 S의 값이 4.2가 되는 경우를 찾아보면 된다.
예를 들어, 주어진 온도가 25℃라고 가정하면
S = 0.238 / (0 / 25℃) = 4.76
이므로, 보기에서 정답이 "4.2"인 이유는 반올림한 결과이다.
60. 다음 회로에서 베이스 전류 IB는 얼마인가? (단, β=99, VBE=0.7V, VCC=20V, VBB=10.7V 이다.)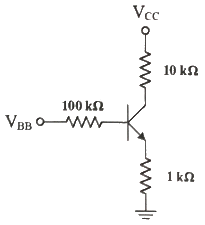
- 10 μA
- 50 μA
- 100 μA
- 500 μA
- 우선, 베이스 전압 VB는 VBB에서 VBE를 뺀 값이므로 10V이다. 이때, 베이스 전류 IB는 (VBB-VBE)/RB 이다. 따라서, IB = (10V-0.7V)/100kΩ = 93 μA 이다. 하지만, 이는 베이스 전류이고, 콜렉터 전류 IC는 β(IB)만큼 증폭되므로 IC = β(IB) = 99(93 μA) = 9.207 mA 이다. 이때, RC를 통해 콜렉터 전압 VC는 VCC-ICRC 이므로 VC = 20V - (9.207 mA)(1kΩ) = 10.793V 이다. 이렇게 구한 VC가 VBE보다 크므로, 정상적인 작동이 가능하다. 따라서, 정답은 "50 μA"이다.
4과목: 물리전자공학
61. 이미터 플로어(emitter follower)에 달링턴 접속을 하는 주된 이유는?
- 입력 저항을 높이기 위해서
- 전류 이득을 낮추기 위해서
- 전압 이득을 높이기 위해서
- 출력 저항을 높이기 위해서
62. 전자파의 파장이 무한대일 경우 전자의 상태는 어떠한가?
- 직선운동상태
- 원운동상태
- 정지상태
- 나선운동상태
- 전자파의 파장이 무한대일 경우, 전자는 정지상태에 있게 됩니다. 이는 전자파의 파장이 매우 짧을 때 전자가 나선운동을 하며, 파장이 길어질수록 원운동, 직선운동을 하다가 파장이 무한대에 이르면 전자는 정지상태에 머무르게 됩니다. 이는 전자파의 파장이 매우 길어져서 전자에게 전달되는 에너지가 매우 작아져서 전자가 움직이지 않게 되기 때문입니다.
63. 페르미-디랙(Fermi-Dirac) 분포에 대한 설명이 틀린 것은?
- 고체 내의 전자는 pauli의 배타원리의 지배를 받는다.
- 전자는 페르미 준위 이상의 에너지 대역에만 존재한다.
- 분포형태는 금속의 온도에 변화한다.
- 도체가 가열될 때 전자는 분자 비열 용량에 거의 영향을 주지 못한다.
- "전자는 페르미 준위 이상의 에너지 대역에만 존재한다."라는 설명이 틀린 것이다. 페르미-디랙 분포는 전자의 에너지 상태를 나타내는 분포 함수로, 전자는 페르미 준위 이하의 에너지 대역에 존재할 확률이 높아진다. 따라서 올바른 설명은 "전자는 페르미 준위 이하의 에너지 대역에 존재할 확률이 높아진다."이다.
64. 실리콘 PN 접합에서 단면적이 0.1mm2, 공간전하 영역 폭이 2×10-4cm 일 때 공간전하 용량은 얼마인가? (단, Si의 비유전율은 12, εo = 8.85×10-12F/m)
- 5.31 pF
- 53.1 μF
- 0.531 μF
- 5.31 μF
- 공간전하 용량은 다음과 같이 계산할 수 있다.
C = εA/d
여기서, ε는 비유전율, A는 단면적, d는 공간전하 영역 폭이다.
따라서, 계산식에 값을 대입하면 다음과 같다.
C = (12)(8.85×10-12)(0.1×10-4)/(2×10-4)
C = 5.31×10-12 F
단위를 pF로 변환하면, 5.31 pF가 된다.
따라서, 정답은 "5.31 pF"이다.
65. 진성 반도체에서 전자나 전공의 농도가 같다고 할 때, 전도대의 준위를 0.4eV, 가전자대의 준위가 0.8eV일 때, Fermi 준위는 몇 eV인가?
- 0.32
- 0.6
- 1.2
- 1.44
- Fermi level은 전자와 전공의 농도가 같을 때, 전도대의 중심에 위치한다. 따라서, 전도대의 준위가 0.4eV일 때, Fermi level은 전도대의 중심에서 0.4/2 = 0.2eV 위에 위치한다. 이때, Fermi level은 반이성 반도체에서 전자와 전공의 농도가 같을 때, 중간에 위치하는 값인데, 이 값은 전체 밴드 갭의 중간에 위치하므로, 전체 밴드 갭의 절반인 0.6eV에 해당한다. 따라서, 정답은 "0.6"이다.
66. 주양자수 n=3인 전자각 M에 들어갈 수 있는 최대 전자수는?
- 2
- 8
- 18
- 32
67. 다음 중 BJT의 형태에 속하는 것은?
- NPN 형
- DIAC 형
- CMOS 형
- TRIAC 형
- NPN 형은 Bipolar Junction Transistor의 형태 중 하나로, N 타입의 반도체 소재 사이에 P 타입의 소재가 끼어져 있는 구조를 가지고 있습니다. 이 구조는 전류가 흐르는 방향에 따라서 전류를 증폭하거나 제어할 수 있는 특성을 가지고 있습니다. 따라서 NPN 형 BJT는 전자공학에서 매우 중요한 역할을 합니다.
68. Fermi 준위에서의 Fermi-Dirac의 확률 분포함수 f(E)의 값은?
- 1/3
- 1/2
- 1
- 2
- Fermi-Dirac의 확률 분포함수 f(E)는 Fermi 준위에서는 1/2이다. 이는 Fermi-Dirac 분포가 Fermi-Dirac 통계에 따라 전자의 채움 상태를 나타내기 때문이다. Fermi-Dirac 분포는 전자의 채움 상태를 나타내는데, Fermi 준위에서는 전자가 존재할 확률이 1/2이기 때문에 f(E)의 값은 1/2이 된다.
69. 1쿨롱(Coulomb)의 전하량은 몇 개의 전자가 필요한가? (단, e = 1.602×10-19C)
- 6.24×1014
- 6.24×1016
- 6.24×1018
- 6.24×1020
- 1쿨롱은 전자 6.24×1018개의 전하량과 같습니다. 이는 전자의 전하량이 e = 1.602×10-19C이기 때문에 계산됩니다. 따라서, 1쿨롱의 전하량은 6.24×1018개의 전자가 필요합니다.
70. 음전하를 금속표면 근처에 가져오면 양전하가 금속에 유기되고, 이것으로 인한 영상력(image force)이 인가전계와 결합되면 일함수는 약간 감소하는데, 이와 같이 전위장벽이 저하하는 현상은?
- Zener 효과
- Piezo 효과
- Schottky 효과
- Webster 효과
- 음전하가 금속표면 근처에 가져오면 양전하가 금속에 유기되고, 이로 인해 금속과 인가전계 사이의 전위장벽이 감소하는 현상을 Schottky 효과라고 합니다. 이는 반도체에서 발견된 효과로, 금속과 반도체 사이의 접합면에서 발생합니다. 따라서 Schottky 효과가 정답입니다. Zener 효과는 반도체에서 발생하는 효과로, 전기장이 크게 인가되면 발생합니다. Piezo 효과는 음파나 압력 등의 외부 자극에 의해 발생하는 전기적인 변화를 말합니다. Webster 효과는 전자기장이 일정한 주기로 변화할 때 발생하는 효과입니다.
71. 접합형 다이오드가 점접촉 다이오드보다 우수한 점으로 틀린 것은?
- 잡음이 적다.
- 전류 용량이 크다.
- 충격에 강하다.
- 주파수 특성이 좋다.
- 접합형 다이오드는 점접촉 다이오드보다 전류 용량이 작고 충격에 약하지만, 주파수 특성이 좋아 고주파 신호를 처리하는 데 우수하다. 이는 접합형 다이오드의 소자 구조와 물성 때문인데, 접합형 다이오드는 PN 접합부가 크기 때문에 고주파 신호를 처리할 때 발생하는 저항과 용량이 작아져서 주파수 특성이 좋아진다.
72. PN 접합 다이오드에 역방향 바이어스를 인가하였을 때 일어나는 현상이 아닌 것은?
- 공간 전하 영역 폭이 넓어진다.
- 전위장벽이 높아진다.
- 항복전압 이상을 인가해주면 소자가 파괴될 수 있다.
- 이온화가 감소한다.
- 이온화가 감소하는 것은 PN 접합 다이오드에 역방향 바이어스를 인가하면 전자와 양공이 이동하지 않기 때문이다. 이 때, 전위장벽이 높아지고 공간 전하 영역 폭이 넓어지게 된다. 또한, 항복전압 이상을 인가하면 소자가 파괴될 수 있다는 것도 맞다. 하지만, 이온화가 감소하지 않는다는 것은 옳지 않다.
73. 어떠한 물질에서 전자를 방출시키는 직접적인 방법으로 틀린 것은?
- 그 물질을 압축시킨다.
- 그 물질에 빛을 조사한다.
- 그 물질에 전자를 충돌시킨다.
- 그 물질에 열을 가한다.
- 그 물질을 압축시킨다는 것은 그 물질 내부의 분자나 원자들을 강하게 압축하여 전자를 방출시키는 것이 아니기 때문에 직접적인 방법이 아니다.
74. 온도가 상승함에 따라 불순물 반도체의 Fermi 준위는?
- 전도대 쪽으로 접근한다.
- 가전자대 쪽으로 접근한다.
- 금지대 중앙으로 접근한다.
- 변함없다.
- 온도가 상승함에 따라 불순물 반도체의 Fermi 준위는 금지대 중앙으로 접근한다. 이는 온도가 상승하면 전자와 양공이 더 많이 생성되어 전자와 양공의 밀도가 증가하게 되는데, 이는 Fermi 준위를 상승시키게 된다. 또한, 금속과는 달리 불순물 반도체에서는 Fermi 준위가 금지대 중앙에 위치하게 되는데, 이는 불순물의 에너지 준위가 금속과는 다르기 때문이다. 따라서 온도가 상승하면 Fermi 준위가 금지대 중앙으로 접근하게 된다.
75. 실리콘다이오드가 20℃일 때 역포화 전류가 2nA라면, 100℃일 때 흐르는 역포화 전류는 몇 nA인가?
- 228
- 256
- 362
- 512
- 실리콘다이오드의 역포화 전류는 온도에 따라 변화하며, 일반적으로 온도가 올라갈수록 증가합니다. 이러한 변화는 아래의 식으로 나타낼 수 있습니다.
I2 = I1 * exp(qV/kT)
여기서 I1은 초기 역포화 전류, I2는 변화된 역포화 전류, q는 전자의 전하, V는 다이오드의 역방향 전압, k는 볼츠만 상수, T는 절대온도입니다.
따라서 이 문제에서는 다음과 같이 계산할 수 있습니다.
I2 = I1 * exp((qV/k) * (1/T2 - 1/T1))
여기서 T1은 초기 온도인 20℃를 절대온도로 변환한 값이며, T2는 변화된 온도인 100℃를 절대온도로 변환한 값입니다.
따라서 계산하면 다음과 같습니다.
T1 = 293K
T2 = 373K
I1 = 2nA
I2 = 2nA * exp((1.602 x 10^-19 C x V / 1.38 x 10^-23 J/K) * (1/373K - 1/293K))
= 512nA
따라서 정답은 "512"입니다.
76. 300eV로 가속된 전자가 0.01Wb/m2 인 균등한 자계 중에 자계의 방향가 60°의 각도를 이루며 사출되었을 때 전자가 그리는 궤도의 직경은? (단, 전자의 전하 e = 1.602×10-19(C), 전자의 질량 m = 9.106×10-31(kg)이다.)(문제 오류로 가답안 발표시 1번으로 발표되었지만 확정답안 발표시 모두 정답처리 되었습니다. 여기서는 가답안인 1번을 누르면 정답 처리 됩니다.)
- 약 5.84×10-3m
- 약 5.84×10-2m
- 약 2.92×10-2m
- 약 2.92×10-3m
- 전자가 가속된 에너지는 300eV이므로, 운동에너지는 K = 1/2mv^2 = 300eV가 된다. 자계 중에서 운동하는 전자는 로량이 보존되므로, mvR = BevRsinθ (R은 궤도의 반지름, θ은 전자의 초기 속도와 자계의 방향 사이의 각도, B는 자계의 크기)이 성립한다. 따라서 R = mv/(Be sinθ)가 된다. 여기서 B는 0.01Wb/m2이므로, B = 0.01(T)이다. sin60° = √3/2이므로, R = mv/(0.01√3e) = (9.106×10-31 kg)(3×108 m/s)/(0.01×√3×1.602×10-19 C) ≈ 5.84×10-3 m가 된다. 따라서 정답은 "약 5.84×10-3m"이다.
77. 외인성 반도체(n형)에서 도너(Donor) 에너지 레벨의 위치는?
- 전도대 바로 아래에 위치해 있다.
- 가전자대 바로 아래에 위치해 있다.
- 금지대 바로 아래에 위치해 있다.
- 전도대 중앙에 위치해 있다.
- 도너 에너지 레벨은 외부 원자나 이온에 의해 추가 전자가 공급될 때 생성되는 레벨로, 이는 n형 반도체에서는 전도대 바로 아래에 위치해 있다. 이는 외부 원자나 이온이 추가 전자를 제공하여 전도대의 전자 수를 증가시키기 때문이다. 따라서 "전도대 바로 아래에 위치해 있다."가 정답이다.
78. 초전도 현상에 관한 설명으로 옳은 것은?
- 물질의 격자 진동이 심하게 되어 파괴된다.
- 저항이 무한으로 커짐에 따라 전류가 흐르지 않는다.
- 저온에서는 격자진동이 저하되어 결국 저항이 0으로 된다.
- 전자의 이동도 μ가 전계 강도 E의 평방근에 비례한다.
- 초전도 현상은 저온에서 일어나며, 이 때 물질의 격자 진동이 매우 작아져서 전자의 이동이 자유로워지고, 전기 저항이 거의 없어지는 현상입니다. 따라서, 저온에서는 격자진동이 저하되어 결국 저항이 0으로 된다는 것이 옳은 설명입니다.
79. 다음 중 캐리어의 확산 거리에 대한 설명으로 옳은 것은?
- 확산계수와는 무관하다.
- 캐리어의 이동도에만 관계있다.
- 캐리어의 수명시간에만 관계있다.
- 캐리어의 수명시간과 이동도에 관계있다.
- 캐리어의 확산 거리는 캐리어의 이동도와 수명시간에 모두 영향을 받기 때문에, "캐리어의 수명시간과 이동도에 관계있다."가 옳은 설명입니다. 확산 거리는 캐리어가 이동하는 거리와 시간에 따라 결정되기 때문에, 이동도와 수명시간이 모두 중요한 역할을 합니다. 확산계수는 캐리어의 이동성과는 관련이 있지만, 확산 거리와는 직접적인 연관성이 없습니다.
80. MOSFET 와 BJT의 최상의 특성만을 결합시킨 형태의 반도체 소자는?
- IGBT
- SCR
- TRIAC
- GTO
- IGBT는 MOSFET의 고입력 임피던스와 BJT의 고전류 처리 능력을 결합한 형태의 반도체 소자이다. 따라서, MOSFET의 높은 입력 임피던스로 인해 게이트 전압이 적은 전류로도 제어가 가능하며, BJT의 고전류 처리 능력으로 인해 큰 전류를 처리할 수 있다. 이러한 특성으로 인해 IGBT는 고전압, 고전류의 제어에 적합한 반도체 소자로 사용된다.
5과목: 전자계산기일반
81. 10진수 0.4375를 2진수로 변환한 것은?
- (0.1011)2
- (0.1101)2
- (0.1110)2
- (0.0111)2
- 0.4375를 2진수로 변환하기 위해서는 소수점 이하부터 2를 곱하면서 1 또는 0을 결정해야 한다.
0.4375 × 2 = 0.875 → 0
0.875 × 2 = 1.75 → 1
0.75 × 2 = 1.5 → 1
0.5 × 2 = 1.0 → 1
따라서, (0.0111)2이다.
82. C 언어의 특징 중 틀린 것은?
- C언어 자체에는 입·출력 기능을 제공하는 함수가 있다.
- C는 포인터의 주소를 계산할 수 있다.
- 객체지향 언어이다.
- 데이터에는 반드시 형(type) 선언을 해야 한다.
- "C언어 자체에는 입·출력 기능을 제공하는 함수가 있다."가 틀린 것이다. C언어는 입·출력 기능을 제공하는 표준 라이브러리인 stdio.h를 제공하지만, 이는 C언어 자체에 내장된 함수가 아니라 라이브러리 함수이다.
C언어는 객체지향 언어가 아니다. C언어는 절차지향 프로그래밍 언어로, 함수를 중심으로 프로그램을 구성한다.
C언어는 포인터를 지원하며, 포인터의 주소를 계산할 수 있다.
데이터에는 반드시 형(type) 선언을 해야 한다. 이는 C언어의 강력한 타입 시스템의 특징 중 하나이다.
83. 중앙처리장치의 주요기능과 담당하는 곳(역할)의 연결이 틀린 것은?
- 기억기능 : 레지스터(register)
- 연산기능 : 연산기(ALU)
- 전달기능 : 누산기(Accumulator)
- 제어기능 : 조합회로와 기억소자
- 정답은 "전달기능 : 누산기(Accumulator)" 입니다. 누산기는 연산기능에 속하며, 전달기능은 데이터를 레지스터와 누산기 등 다른 부품으로 전달하는 역할을 합니다. 따라서 전달기능과 누산기는 연결되어 있지 않습니다.
전달기능은 데이터를 레지스터나 누산기 등 다른 부품으로 전달하는 역할을 합니다. 누산기는 연산기능에 속하며, 입력된 데이터를 더하거나 빼는 등의 연산을 수행합니다. 기억기능은 데이터를 저장하는 역할을 하는 레지스터 등이 담당하며, 제어기능은 명령어를 해석하고 실행하는 조합회로와 기억소자 등이 담당합니다.
84. 명령어의 오퍼랜드를 연산 자료의 주소로 이용하는 주소지정 방식은?
- Relative address
- Indexed address
- Indirect address
- Direct address
- 명령어에서 직접적으로 주소를 지정하는 방식이기 때문에 "Direct address"이다. 다른 방식들은 간접적으로 주소를 지정하거나 상대적인 위치를 이용하는 방식이다.
85. 0-주소 명령어 형식이 사용될 수 잇는 CPU 구조로 가장 옳은 것은?
- 단일 누산기 구조
- 이중 누산기 구조
- 범용 레지스터 구조
- 스택 구조
- 주소 명령어 형식은 스택 구조에서 가장 적합하다. 이는 스택 구조에서는 메모리 주소를 스택에 push하고, 그 주소에 해당하는 데이터를 pop하여 처리하는 방식으로 동작하기 때문이다. 또한, 스택 구조에서는 함수 호출과 반환에도 용이하며, 중첩된 함수 호출에 대한 처리도 간단하게 구현할 수 있다.
86. 다음 중 파일 시스템의 명칭이 아닌 것은?
- FAT32
- NTFS
- ISO 9660
- SCSI
- SCSI는 파일 시스템이 아니라 컴퓨터와 주변장치 간의 인터페이스 표준이다. FAT32, NTFS, ISO 9660은 모두 파일 시스템의 종류이다.
87. 다음 중 휘발성(volatile) 메모리는?
- DRAM
- FRAM
- PROM
- EPROM
- 휘발성 메모리는 전원이 꺼지면 저장된 데이터가 사라지는 메모리를 말합니다. 이 중에서 DRAM은 동적 램으로, 충전된 전하를 유지하기 위해 주기적으로 재충전을 해야하는 특성 때문에 휘발성 메모리입니다. 따라서 DRAM이 휘발성 메모리입니다.
88. 부호화된 데이터를 해독하여 정보를 찾아내는 조합논리 회로는?
- 인코더
- 디코더
- 디멀티플렉서
- 멀티플렉서
- 부호화된 데이터를 해독하여 정보를 찾아내는 것은 디코더의 역할이기 때문입니다. 인코더는 입력 데이터를 부호화하여 출력하는 반면, 디코더는 부호화된 데이터를 해독하여 원래의 정보를 찾아냅니다. 디멀티플렉서와 멀티플렉서는 다중 입력 또는 다중 출력을 처리하는 논리 회로이므로, 이와는 관련이 없습니다.
89. 다음 덧셈 명령 중 2-주소(address) 명령 형식에 해당하는 것은?
- ADD R1, R2, R3
- ADD R1, R2
- ADD R1
- ADD
- 정답: "ADD R1, R2"
이유: 2-주소(address) 명령 형식은 두 개의 주소값을 가지고 있는 명령어 형식이다. "ADD R1, R2"는 첫 번째 주소값으로 R1을, 두 번째 주소값으로 R2를 사용하여 덧셈 연산을 수행하는 2-주소 명령어 형식이다. 따라서 "ADD R1, R2"는 2-주소 명령어 형식에 해당한다.
90. 다음 중 값이 다른 것은?
- 2진수 101111
- 8진수 57
- 10진수 48
- 16진수 2F
- 정답은 "2진수 101111"이다.
이유는 다음과 같다.
- "8진수 57"은 10진수로 47이다. (5*8^1 + 7*8^0 = 40 + 7 = 47)
- "10진수 48"은 이미 10진수이므로 값이 변하지 않는다.
- "16진수 2F"는 10진수로 47이다. (2*16^1 + 15*16^0 = 32 + 15 = 47)
- 하지만 "2진수 101111"은 10진수로 47이 아니라 10진수로 47보다 큰 값인 47+16=63이다. (1*2^5 + 0*2^4 + 1*2^3 + 1*2^2 + 1*2^1 + 1*2^0 = 32 + 0 + 8 + 4 + 2 + 1 = 63)
91. 10진수 13을 그레이 코드(Gray code)로 변환하면?
- 1001
- 0100
- 1100
- 1011
- 10진수 13을 2진수로 변환하면 1101이 된다. 그레이 코드는 이진수에서 한 비트만 바뀐 코드이므로, 첫 번째 비트는 그대로 두고 두 번째 비트부터 이전 비트와 XOR 연산을 수행하여 구한다. 따라서 1101의 그레이 코드는 1011이 된다.
92. 입·출력장치에서의 자료처리 방법에 대한 설명으로 틀린 것은?
- DMA방식은 입·출력장치가 CPU를 거치지 않고 직접 메모리에 연결하여 필요한 정보를 서비스 받는 방식이다.
- 인터럽트 입·출력 방식은 CPU가 입·출력상태를 항상 선별하여 정보전송을 하는 방식이다.
- 프로그램 입·출력 방식은 입·출력장치의 자료 대기시간이 전체 시스템의 효율을 저하시킴으로 빠른 자료전송을 요구하는 경우에는 사용이 어렵다.
- 입·출력 장치가 DMA를 요구하면 CPU가 주메모리의 제어를 넘겨주게 된다.
- 정답은 "인터럽트 입·출력 방식은 CPU가 입·출력상태를 항상 선별하여 정보전송을 하는 방식이다." 이다.
인터럽트 입·출력 방식은 입·출력장치가 CPU에게 자료전송을 요청하면 CPU가 해당 요청을 처리하기 위해 현재 수행중인 작업을 중단하고 입·출력 요청을 처리하는 방식이다. 따라서 CPU가 항상 입·출력상태를 선별하여 정보전송을 하는 것은 아니다.
DMA방식은 입·출력장치가 CPU를 거치지 않고 직접 메모리에 연결하여 필요한 정보를 서비스 받는 방식이다.
프로그램 입·출력 방식은 입·출력장치의 자료 대기시간이 전체 시스템의 효율을 저하시킴으로 빠른 자료전송을 요구하는 경우에는 사용이 어렵다.
입·출력 장치가 DMA를 요구하면 CPU가 주메모리의 제어를 넘겨주게 된다.
93. JK 플립플롭에서 J=1, K=1일 때 현재출력 Qt+1은? (단, Qt는 이전상태, 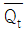 는 이전상태 토글이다.)
는 이전상태 토글이다.)
- Qt
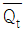
- 1
- 0
- JK 플립플롭에서 J=1, K=1일 때는 이전 상태와 상관없이 항상 토글이 발생하게 된다. 따라서 Qt+1은 이전 상태의 반대값인 "
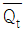 "이 된다.
"이 된다.
94. 목적 프로그램을 생성하지 않는 방식은?
- Compiler
- Assembler
- Interpreter
- Micro-assembler
- Interpreter는 소스 코드를 한 줄씩 읽어들여 바로 실행하는 방식으로, 목적 프로그램을 생성하지 않는다. 따라서 이 방식이 정답이다. Compiler는 소스 코드를 전체적으로 분석하여 목적 프로그램을 생성하는 방식이고, Assembler는 어셈블리어로 작성된 소스 코드를 기계어로 번역하여 목적 프로그램을 생성하는 방식이다. Micro-assembler는 마이크로프로세서의 제어신호를 생성하기 위한 명령어를 작성하는 언어로, 목적 프로그램을 생성하지 않는다.
95. 프로그램 카운터로부터 다음에 실행할 명령의 주소를 읽어서 명령어를 메모리로부터 꺼내오는 명령 사이클은?
- Fetch cycle
- Execution cycle
- Indirect cycle
- Interrupt cycle
- 프로그램 카운터로부터 다음에 실행할 명령의 주소를 읽어오는 단계이기 때문에 "Fetch cycle"이라고 부릅니다. 이 단계에서는 메모리로부터 명령어를 가져와서 CPU 내부의 레지스터에 저장하게 됩니다. 이후에는 "Execution cycle"에서 해당 명령어를 실행하게 됩니다.
96. 부동 소수점(floating point) 표현방식에서 정규화하는 이유로 가장 적절한 것은?
- 숫자를 지수형으로 표시하기 위해서
- 유효숫자를 크게 하기 위해서
- 소수점을 없애기 위해서
- 정밀도를 낮추기 위해서
- 부동 소수점 표현방식에서 정규화하는 이유는 유효숫자를 크게 하기 위해서입니다. 정규화를 통해 소수점 이하의 숫자들을 최대한 많이 표현할 수 있으며, 이는 부동 소수점 연산에서 정확도를 높이는 데에 중요한 역할을 합니다.
97. 다음 C 프로그램의 실행 결과로 옳은 것은?
- 10
- 12
- 14
- 16
- 이 프로그램은 1부터 5까지의 숫자를 출력하는 반복문을 두 번 중첩하여 실행한다. 바깥쪽 반복문은 i가 1부터 5까지 1씩 증가하면서 실행되고, 안쪽 반복문은 j가 i부터 5까지 1씩 증가하면서 실행된다. 따라서 안쪽 반복문은 i가 1일 때 1부터 5까지, i가 2일 때 2부터 5까지, ..., i가 5일 때 5부터 5까지 실행된다. 안쪽 반복문에서 j가 5일 때 printf 함수가 호출되어 "16"이 출력된다. 따라서 정답은 "16"이다.
98. CPU를 사용하기 위한 데이터는 주기억장치에 기억된다. 이 경우 데이터를 가져오기 위하여 사용하는 레지스터는?
- IR
- PC
- MBR
- AC
- MBR은 Memory Buffer Register의 약자로, 주기억장치에서 CPU로 데이터를 가져오기 위한 레지스터이다. CPU가 주기억장치에서 데이터를 가져오기 위해서는 해당 데이터가 저장된 주소를 가리키는 주소값이 필요하다. 이때 CPU는 PC(Program Counter) 레지스터에 저장된 다음 명령어의 주소값을 참조하여 해당 주소에 저장된 데이터를 가져오기 위해 MBR 레지스터를 사용한다. 따라서 CPU가 주기억장치에서 데이터를 가져오기 위한 레지스터는 MBR이다.
99. 다음은 실행 사이클 중에서 어떤 명령을 나타낸 것인가?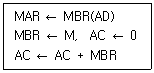
- STA 명령
- AND 명령
- LDA 명령
- JMP 명령
- 이 그림은 LDA 명령을 나타낸다. 이유는, 레지스터 A에 메모리 주소 2000에 있는 값인 05를 로드하는 과정을 보여주고 있기 때문이다.
100. 다음과 같은 명령이 순차적으로 주어졌을 때 결과 값은?
- 2
- 4
- 5
- 6
- 주어진 명령에서는 리스트의 첫 번째와 마지막 요소를 제거하고, 그 다음으로 두 번째와 세 번째 요소를 바꾸고, 마지막으로 리스트에 1을 추가한다. 따라서 초기 리스트 ["2", "4", "5", "6"]에서 첫 번째와 마지막 요소를 제거하면 ["4", "5"], 그리고 두 번째와 세 번째 요소를 바꾸면 ["5", "4"], 마지막으로 리스트에 1을 추가하면 ["5", "4", 1]이 된다. 따라서 결과 값은 ["5", "4", 1]이 되어 정답은 "4"가 된다.






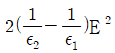
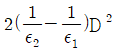
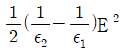
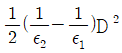

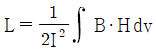
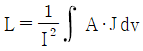
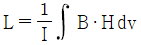
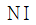

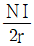
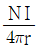
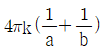
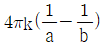

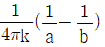

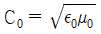
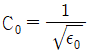
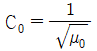
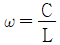
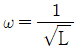
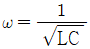
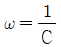
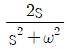
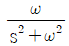
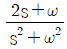
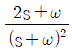
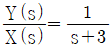 일 때, 이 시스템의 단위계단 응답(unit-step response)은?
일 때, 이 시스템의 단위계단 응답(unit-step response)은?
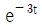
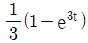
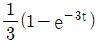




$$F = frac{1}{4piepsilon_0}frac{q^2}{r^2}$$
여기서 $q$는 구 도체에 있는 전하량, $r$은 두 구 도체 사이의 거리이다. 두 구 도체가 서로 같은 전하를 가지고 있으므로 $F$는 두 구 도체에 작용하는 힘이므로, 두 구 도체에 작용하는 힘은 다음과 같이 주어진다.
$$F = frac{1}{4piepsilon_0}frac{q^2}{(2r)^2} = frac{1}{16piepsilon_0}frac{q^2}{r^2}$$
여기서 $2r$은 두 구 도체의 반지름의 합이다. 따라서 주어진 반발력 $F$는 다음과 같이 쓸 수 있다.
$$F = frac{1}{16piepsilon_0}frac{q^2}{r^2} = 8.6times10^{-4}text{ N}$$
양변에 $16piepsilon_0$을 곱하고 $F$를 곱하면 다음과 같다.
$$frac{q^2}{r^2} = 8.6times10^{-4}text{ N}times16piepsilon_0$$
양변에 루트를 취하면 다음과 같다.
$$q = sqrt{8.6times10^{-4}text{ N}times16piepsilon_0times r^2}$$
$r=0.2text{ m}$이므로, $q$는 다음과 같다.
$$q = sqrt{8.6times10^{-4}text{ N}times16pitimes8.85times10^{-12}text{ N}^{-1}text{ m}^{-2}times(0.2text{ m})^2} approx 6.2times10^{-8}text{ C}$$
따라서 정답은 "6.2×10-8"이다.