1과목: 기하광학 및 광학기기
1. 다음 중 빛의 성질에 관한 설명으로 틀린 것은?
- 입자적 성질을 나타내는 현상은 광전효과가 있다.
- 전자기파이며 빛이 직진하는 성질 때문에 반사와 굴절이 된다.
- 빛의 파동 성질을 나타내는 현상으로는 간섭과 회절이 있다.
- 빛은 음향입자(phonon)의 흐름이다.
2. 초점거리가 60cm 인 대물렌즈와 초점거리가 3cm 인 대안 렌즈로 만든 망원경의 배율은?
- 10
- 20
- 40
- 180
3. 초점거리가 각각 10cm 인 볼록렌즈와 오목렌즈를 동일 광축 위에 나란히 놓아 한 개의 새로운 렌즈를 만든다면 새로운 렌즈의 유효초점거리와 렌즈의 종류는? (단, 두 렌즈 사이의 간격은 2.5cm이다.)
- 25cm, 볼록렌즈
- 40cm, 볼록렌즈
- 25cm, 오목렌즈
- 40cm, 오목렌즈
4. “빛이 한 점에서 다른 점으로 전파될 때 그 광선의 경로는 광학적 길이가 최소화되는 경로를 택한다”는 원리를 설명 한 사람은?
- Fermat
- Snell
- Huygens
- Young
5. 구면거울 2m 앞에 물체가 있을 때 상의 거리가 50cm라면 이 거울의 곡률반경은 몇 cm 인가?
- 40
- 60
- 80
- 100
6. He-Ne 레이저에서 발생한 평행광선이 광축을 따라서 단일 볼록렌즈에 의해 집속될 때, 초점에 한점으로 모이지 않고 크기를 갖는 원으로 모이는 것은 무슨 수차 때문인가?
- 구면수차
- 코마수차
- 만곡수차
- 왜곡수차
7. 다음 중 종색수차를 최소화하는 방법으로 적절한 것은?
- 필름을 벤딩한다.
- 비구면 가공을 한다.
- 접촉 이중렌즈를 사용한다.
- 중간에 스톱이 있는 대칭형 구조의 렌즈를 사용한다.
8. 그래프에서 undercorrected spherical aberration에 관한 광축으로부터의 높이(h)와 초점거리(f)의 관계를 옳게 표현한 것은?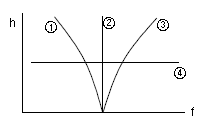
- ①
- ②
- ③
- ④
9. 15 디옵터의 얇은 렌즈 두 개가 8cm 떨어져 있다면 두 렌즈에 의한 유효초점거리는 몇 cm 인가? (단, 두 렌즈는 모두 공기 중에 있다.)
- 10
- 12.5
- 15
- 17.5
10. 다음 중 주경이 오목 거울, 부경이 볼록 거울로 구성된 망원경은?
- 뉴턴 망원경
- 공심형 망원경
- 그레고리형 망원경
- 카세그레인형 망원경
11. 크라운 유리의 C(H)선에 대한 굴절률이 1.5204, D(Na) 선에 대한 굴절률이 1.5230, 그리고 F(H)선에 대한 굴절률이 1.5293 일 때, 이 유리의 색분산과 관련된 아베수(Abbe's number)는 약 얼마인가?
- 45.2
- 58.8
- 69.4
- 81.6
12. 근축광선 이론을 도입할 경우, 다음 중 Snell의 굴절 법칙을 바르게 나타낸 것은?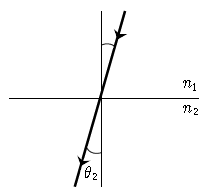
- n1·θ1=n2·θ2
- n1·√θ1=n2·√θ2
- n1·θ2=n2·θ1
- n1·√θ2=n2·√θ1
13. 굴절률이 n 인 매질에서 광선이 d 만큼 이동할 때 광선 도달행렬(lay-transfer matrix)은 어떻게 표현되는가?
14. 1mm 당 10개의 줄무늬가 있는 물체에 대한 두 광학계의 MTF 값이 각각 0.7 과 0.8 이다. 두 광학계를 동시에 사용할 때, 전체 MTF 값은 얼마인가?
- 0.1
- 0.56
- 0.7
- 56
15. 그림과 같이 입사각 θ1 으로 빛이 광학적으로 밀한 매질(n1)에서 광학적으로 소한 매질(n2)로 입사할 때, 예측되는 굴절광의 경로는 어느 것인가?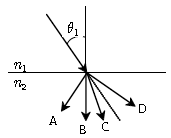
- A
- B
- C
- D
16. 배율이 5 인 천체 망원경의 두 렌즈가 30cm 떨어져 있을 때 대물렌즈와 대안렌즈의 초점거리는 각각 몇 cm 인가?
- 대물렌즈 25cm, 대안렌즈 5cm
- 대물렌즈 5cm, 대안렌즈 25cm
- 대물렌즈 30cm, 대안렌즈 5cm
- 대물렌즈 5cm, 대안렌즈 30cm
17. 깊이 2m 인 수영장에 굴절률이 5/3인 액체로 채워져 있다. 수영장의 표면을 원형의 판으로 덮어 수영장 바닥에 놓여 있는 점광원의 빛이 새어 나가지 못하게 하려면 판의 최소 반지름은 약 몇 m 로 하여야 하는가?
- 0.5
- 1
- 1.5
- 2
18. 다음 중 렌즈의 초점을 구하는 방법이 아닌 것은?
- 노달 슬라이드법
- Fourier 방법
- 자동시준화 방법
- Abbe 방법
19. 물체의 오른쪽으로 10cm 떨어진 곳에 놓인 렌즈가 물체의 5 배인 허상을 만든다면 렌즈의 굴절능은 몇 D 인가? (단, 물체와 렌즈는 공기 중에 놓여 있다.)
- 6
- 7
- 8
- 9
20. 어떤 물체를 f-4 에 1/400 초로 촬영하는 것이 적당한 노출이라면 f-8 인 경우 적절한 노출시간은 몇 초인가?
- 1/25
- 1/50
- 1/100
- 1/200
2과목: 파동광학
21. 박막 도파로에 대한 설명으로 틀린 것은?
- 박막 도파로에는 TEM 파가 전송되지 못한다.
- 일반적으로 박막 도파로의 유효두께는 박막두께보다 크다.
- 박막 도파로는 도파되는 빛의 파장이 짧을수록 제작이 용이하다.
- 도파로의 도파모드 측정을 통하여 광학 박막의 굴절률 결정이 가능하다.
22. 다음 중 홀로그램에 대한 설명으로 옳은 것은?
- 홀로그램이 기록된 건판의 일부만 사용하여도 기록된 물체의 3차원 재생상을 볼 수 있다.
- 홀로그램은 물체로부터 나온 광파의 세기를 기록한 것 이다.
- 일반적으로 투과형 홀로그램이 반사형 홀로그램에 비해 백색광에서의 색번짐(chromatic blur)이 적다.
- 온셋기준파(onset reference) 홀로그램이 오프셋기준파(offset reference) 홀로그램에 비하여 홀로그램 영상의 관찰에 유리하다.
23. 다음의 간섭계 중 진폭분리형 간섭계가 아닌 것은?
- 자민(Jamin) 간섭계
- 마이켈슨(Michelson) 간섭계
- 마하-젠더(Mach-Zehnder) 간섭계
- 프레넬 이중프리즘(biprism) 간섭계
24. 폭 50㎛의 좁고 긴 슬릿 바로 뒤에 초점거리 1m인 블록 렌즈를 놓고 단색광을 수직으로 입사시켰을 때, 렌즈의 초점면에 나타난 회절무늬의 중심에서 첫번째 어두운 중심까지의 거리가 12mm 라면 이 빛의 파장은 몇 ㎛ 인가?
- 0.49
- 0.55
- 0.60
- 0.68
25. 음향광학 변조기는 투명한 결정이나 유리로 된 물질의 한 끝에 압전소자를 부착하여 초음파를 발생시켜 입력광을 변조시킨다. 투명 매질 내 초음파에 의해 입력광에서 일어나는 광학적 현상은?
- 회절
- 간섭
- 편광 방향의 변화
- 입력광 세기의 변조
26. 광통신용 섬유에서 모드분산(modal dispersion)을 줄이는 방법이 아닌 것은?
- 광섬유 코어의 직경을 작게 한다.
- 코어의 굴절률이 연속적으로 분포하도록 만든다.
- 아베수가 큰 재질로 광섬유를 제작한다.
- 이산화규소유리 광섬유를 사용한다.
27. 광섬유를 이용하여 센서를 구성하려고 한다. 압력이나 진동을 측정하는 광섬유는 어떤 광학적 현상을 이용하는 것인가?
- 복굴절 변화
- 포켈스 효과
- 광탄성 효과
- 패러데이 효과
28. 4.0×1014Hz의 주파수를 가지는 빛이 단위 cm당 10000개의 선을 가지는 회절격자(grating)에 수직으로 입사된다. 이 grating으로 볼 수 있는 스펙트럼의 가장 큰 차수는?
- 0차
- 1차
- 2차
- 3차
29. 파장이 1.5m 이고 빔의 직경이 1mm인 가우스 광속을 렌즈에 입사시켜 지름이 10m 인 광섬유 코어에 집속시키려고 하면, 필요한 렌즈의 초점거리는 약 몇 mm 인가?
- 4.8
- 5.2
- 5.7
- 6.3
30. 나트륨등에서 나오는 노란빛은 5890Å 과 5896Å 의 두 파장으로 되어 있다. 이 빛의 스펙트럼을 회절격자를 사용하여 분해하여 보려고 한다면, 어떤 빛을 사용하여야 하는가? (단, 나트륨등의 기체압력과 온도에 의한 선폭 확대는 무시한다.)
- 격자선 밀도 10 lines/mm 인 5cm × 5cm 회절격자에서 1차 회절된 빛을 사용한다.
- 격자선 밀도 15 lines/mm 인 5cm × 5cm 회절격자에서 1차 회절된 빛을 사용한다.
- 격자선 밀도 5 lines/mm 인 5cm × 5cm 회절격자에서 2차 회절된 빛을 사용한다.
- 격자선 밀도 20 lines/mm 인 5cm × 5cm 회절격자에서 2차 회절된 빛을 사용한다.
31. 굴절률 1.5 인 유리면에 굴절률 1.38 인 MgF2 박막을 한 층 입혀서 550nm 에 대한 반사율이 최소가 되게 하려고 한다. 이 때 필요한 박막의 최소 두께는 약 몇 nm 인가?
- 100
- 153
- 306
- 397
32. 그림과 같은 주기함수 f(x)를 푸리에 급수(Fourier series)로 바르게 표현한 것은?
33. Ψ(x, t)=A sin (ax-bt)의 조화 파동함수가 갖는 속도의 크가와 방향을 올바르게 나타낸 것은? (단, a 와 b 는 양의 상수이다.)
- b/a, +x 방향
- b/a, -x 방향
- a/b, +x 방향
- a/b. -x 방향
34. 신문 사진에 나타나 있는 점 배열들을 보이지 않도록 사진을 부드럽게 하려면 어떤 필터를 사용해야 하는가?
- 저주파 투과 필터
- 고주파 투과 필터
- 광대역 투과 필터
- 홀로그램 필터
35. 공간주파수(Spatial frequency)의 단위는?
- Hz
- cycles/mm
- cycles/s
- lines/s
36. 굴절률이 1.47 인 글리세린 속에 놓인 동전의 겉보기 깊이는 30cm 이다. 실제 깊이는 약 몇 cm 인가?
- 21
- 30
- 44
- 54
37. 각주파수가 ω로써 z 방향으로 진행하는 두 평면 조화파 Eoexp[i(kz1-ωt+øo)] 와 Eoexp[i(kz2-ωt+øo)]가 합성될 때 합성파의 세기는? (단, Eo는 진폭이다.)
- 2E2o[1-cos {k(z1-z2)-2øo}]
- 2E2o[1+cos {k(z1-z2)}]
- 2E2o[1+cos {k(z1-z2)+2øo}]
- 2E2o[1-cos {k(z1-z2)}]
38. 회절격자로부터의 m 차 회절광에 대한 각 분산 (Dm: angular dispersion)의 표현으로 옳은 것은? (단, θm은 m 차 회절광의 격자의 수직면에 대한 회절각, a는 회절격자의 격자간 간격이다.)
39. 다음 중 홀로그램의 특성이 아닌 것은?
- 기준파의 위치가 변하면 상의 크기는 변하지 않으나, 상의 위치는 변화한다.
- 홀로그램을 작은 조각으로 잘라내어도, 각 조각은 물체의 온전한 상을 모두 포함한다.
- 제작된 홀로그램을 밀착 인화(contact printing)하면 동일한 성질의 또 다른 홀로그램을 만들 수 있다.
- 기록광 파장의 2배 파장을 갖는 광으로 홀로그램을 재생할 때, 재생된 상의 횡배율이 2배이면 종배율도 2배이다.
40. 광통신에 주로 사용되는 C-band 의 파장 영역은?
- 800 ~ 900nm
- 1260 ~ 1360nm
- 1365 ~ 1525nm
- 1530 ~ 1562nm
3과목: 광학계측과 광학평가
41. 다음 중 He-Ne 레이저의 발진파장에 해당되는 것은?
- 632.8Å
- 6.328m
- 256nm
- 632.8nm
42. 현미경 검사 표본(KS B 5603)은 직선을 평행으로 그은 격자 모양의 것으로 하고, 1mm 길이에 그어진 직선의 수에 따라 0종, 1종, 2종으로 구분된다. 다음 중 1종에 해당하는 직선의 수는?
- 100
- 300
- 600
- 900
43. 카메라 렌즈의 f 값이 f-2 인 렌즈와 f-4 인 렌즈가 있다. 두 렌즈의 노출 속도비의 값은?
- 1.4
- 2
- 2.8
- 4
44. 대물렌즈의 초점거리 5mm, 광경통 길이 16cm, 투사대안 렌즈의 초점거리 5cm 인 현미경에 길이 25cm 인 카메라가 부착된 현미경 사진장치가 있다. 이 사진 건판상의 총 배율은?
- 80배
- 160배
- 240배
- 320배
45. 색지움(색수차가 소거됨) 렌즈에 대한 설명이 틀린 것은?
- 볼록 크라운렌즈를 전면으로 하고, 오목 프린트 렌즈를 후면으로 하여 결합시켜 만든다.
- C선(H-6562Å)과 F선(H-4861Å) 및 d(He-5876Å)에 대한 색지움렌즈는 3개의 렌즈로 구성한다.
- 색지움 렌즈의 설계시 주로 참고되는 프라운호퍼선으로는 C선과 F선이 있다.
- 색지움 이중렌즈를 통과한 빛은 파장에 상관없이 공통 초점을 가진다.
46. 전체 홈(groove)의 수가 N 인 회절격자에 의해 m 차로 회절되는 빛에 대한 회절격자의 분해능 R 은?
- m · N
- m/N
- N/m
- m · logN
47. 다음 중 뉴턴 원무늬(Newton's rings) 실험을 이용하여 볼록렌즈와 곡률반경을 측정하려 할 때 필요한 값이 아닌 것은?
- 유리의 굴절률
- 사용한 빛의 파장
- 간섭무늬의 차수
- 무늬 중심으로부터의 거리
48. 굴절률(n = 1.5)이 같은 두 렌즈가 30cm 떨어져 있는 광학계의 만곡수차(field curvature)를 제거하고자 한다. 첫 번째 렌즈는 볼록렌즈, 두 번째 렌즈는 오목렌즈이며 두 렌즈 모두 초점거리가 30cm 이다. 이 광학계의 초점거리는 몇 cm 인가?
- 10
- 20
- 30
- 40
49. 다음 중 광학렌즈의 재료로 사용되지 않는 것은?
- PS(Polystyrene)
- PC(Polycarbonate)
- MGO(Magnesium Oxide)
- PMMA(Polymethylmethacrylate)
50. 어떤 쌍안경에 7 x 50 이라는 숫자가 쓰여 있다. 이 쌍안경의 출사동(exit pupil)의 직경은 약 몇 mm 인가?
- 7
- 10
- 50
- 100
51. 광학유리 지도(map)에 관한 설명으로 옳은 것은?
- 일반적으로 Abbe 수가 큰 물질일수록 굴절률도 높다.
- 수평축은 Abbe 수이고, 수직축은 He d선에서의 굴절률이다.
- 크라운(crown)유리의 Abbe 수는 플린드(flint)유리의 Abbe 수보다 작다.
- 플린트(flint)유리의 굴절률은 크라운(crown)유리의 굴절률보다 작다.
52. A 지점에서 발사된 빛이 B 지점에 놓여있는 거울에 반사 되어 A 지점까지 되돌아 오는데 10-6초가 걸렸다면 A 지점 과 B 지점사이의 거리는 몇 m 인가? (단, A 지점과 B 지점 사이는 진공으로 되어있다.)
- 15
- 30
- 150
- 300
53. 그림과 같은 프리즘을 통과하는 광이 프리즘의 빗면을 통과하여 공기 중으로 전파되지 못하도록 하려고 한다. 이 프리즘의 굴절률이 빛의 파장에 관계없이 일정하다면 이 프리즘이 가져야 할 최소 굴절률은 얼마인가?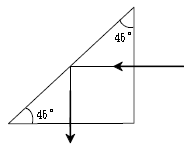
- 1.5
- 2
- √2
- 1/√2
54. 다음 그림과 같이 2차경에서 오목면경을 사용하여 주경의 초점 밖에서 도립상을 얻는 방식의 반사망원경은?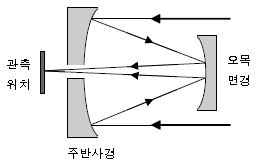
- 카세그레인(Cassegrain) 방식
- 그레고리(Gregory) 방식
- 뉴턴(Newton) 방식
- 쿠테(Coude) 방식
55. 다음 중 일반렌즈용 광학재료가 갖추어야 할 조건이 아닌 것은?
- 무색 투명해야 한다.
- 기계적인 가공성이 좋아야 한다.
- 광학적으로 균질성이 있어야 한다.
- 광학적으로 이방성이 있어야 한다.
56. 정각(꼭의각)이 α이고, 최소편의각이 δm인 분산 프리즘의 굴절률은?
57. 카메라 렌즈의초점거리가 80mm이고, 앞쪽 입사각 렌즈의 크기는 55mm이며, 뒤쪽 출사쪽 렌즈의 크기는 30mm이다. f-수가 1.4인 경우, 이 렌즈의 구경(STOP) 직경은 약 몇 mm 인가?
- 1.45
- 1.8
- 57
- 77
58. 일반적인 광학유리의 구성 원소 중 가장 많이 포함되는 것은?
- Al2O3
- B2O3
- Na2O
- SiO2
59. 사진기의 조리개 구경을 반으로 줄일 경우, 사진기의 f-수와 필름면에 도달하는 빛의 선속밀도에 관한 설명으로 옳은 것은?
- f-수와 선속밀도 모두 반으로 감소
- f-수와 선속밀도 모두 2배 증가
- f-수는 반으로 감소, 선속밀도는 4배 증가
- f-수는 2배 증가, 선속밀도는 1/4로 감소
60. 렌즈의 설계를 위해 참고하여야 할 광학유리의 물성과 무관한 것은?
- 접착성
- 굴절률
- 투과도
- 열팽창 계수
4과목: 레이저 및 광전자
61. 많은 종류의 레이저에서 플라즈마관의 창(Window)이 브루스터(Brewster) 각도로 부착되어 있는 것을 볼 수 있다. 그 이유로 가장 적합한 내용은?
- 가간섭성(coherence)를 좋게 하기 위해
- 회절효과를 줄이기 위해
- 창에서의 반사를 없애기 위해
- 간섭을 줄이기 위해
62. 결정구조 중 전기광학 특성인 포켈스 효과(Pockels effect)를 보이는 구조로 옳은 것은?
- 단축 결정구조를 제외한 전 결정구조
- 쌍축 결정구조를 제외한 전 결정구조
- 중심대칭이 없는 등방성 결정구조를 제외한 전 결정 구조
- 중심대칭이 없는 등방성(isotropic), 단축(uniaxial) 및 쌍축(biaxial) 결정 전부
63. 다음 레이저 중 화학반응에 의한 레이저 발진이 일어날 수 없는 것은?
- DF 레이저
- HF 레이저
- Xe-Cl 레이저
- He-Ne 레이저
64. 다음 중 레이저와 주요 발진 파장의 연결이 틀린 것은?
- CO2 레이저 : 10.6㎛
- 루비 레이저 : 882nm
- ArF 엑시머 레이저 : 193nm
- He-Ne 레이저 : 632.8nm
65. 다음 중 출력이 높아 절단, 용접 등 산업용 공작기계에 많이 사용되는 레이저는?
- He-Ne 레이저
- Ar-ion 레이저
- CO2 레이저
- ArF 레이저
66. 레이저 공진기는 서로 마주 보는 두 개의 거울 사이에서 광속이 반사를 반복하면서 오랫동안 머물도록 고안된 것이다. 이는 어떤 간섭계를 이용한 것인가?
- 트위먼-그린(Twyman-Green)
- 뉴턴(Newton)
- 마흐-젠더(Mach-Zehnder)
- 패브리-페로(Fabry-Perot)
67. 등방성 물질인 클로로포름(CHCl3)에서 관찰할 수 있는 효과는?
- 커(Kerr) 효과
- 포켈스(Pockels) 효과
- 광전(photoelectric) 효과
- 광굴절률(photorefractive) 효과
68. 굴절률 타원체(index ellipsoid) 방정식이 0.4X2+0.4Y2+0.3Z2=1인 매질에서 x 축 방향으로 편극된 광의 굴절률은 약 얼마인가?
- 1.38
- 1.48
- 1.58
- 1.68
69. 펄스폭이 아주 좁은 펄스레이저(10-12s 이하)를 이용하는 분야로 적절하지 않은 것은?
- 정밀 거리 측정
- 전자의 빠른 운동분석
- 광유도 화학반응 분석
- 물질의 정밀한 분광특성 조사
70. 음파를 이용한 광변조는 음파가 만드는 회절격자에 의한 빛의 회절현상을 이용한 것이다. 그림과 같이 음파면에 대해 θ의 각도로 입사하여 다시 같은 각도 θ로 1차 회절 될 때 회절광의 세기가 가장 크게 되는 조건은? (단, λ와 λs는 물질 내의 빛과 음파의 파장이고, n은 물질내의 빛의 굴절률이다.)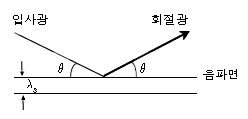
- 2λs sinθ = λ/n
- 2λ sinθ = λs/n
- λs sinθ = λ/n
- λ sinθ=λs/n
71. 그림은 니콜 프리즘(Nicol prism)을 나타낸 것이다. 광선 A와 B에 대하여 바르게 기술한 것은? (단, ↔ 와 ↕ 는 각각 z축, y축 전기장의 진동방향을 나타낸다.)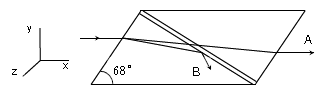
- A는 정상광선(ordinary ray)이고, 전기장은 ↔ 선형 편광된다.
- A는 정상광선(ordinary ray)이고, 전기장은 ↕ 선형 편광된다.
- B는 정상광선(ordinary ray)이고, 전기장은 ↔ 선형 편광된다.
- B는 정상광선(ordinary ray)이고, 전기장은 ↕ 선형 편광된다.
72. 다음 중 제2고조파 발생을 위한 위상정합조건이 아닌 것은? (단, k1, k2, k3는 각 평면파의 위상정수, kω는 파수, nω는 굴절률, n2ω 는 제2고조파의 굴절률이다.)
- k3=k1+k2
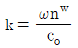
- k2ω=2kω
- n2ω=nω
73. 빛이 등방성의 작은 입자들에 의하여 산란이 일어날 때 만일 입자들의 크기가 파장에 비하여 무시할 수 있을 정도로 작다면, 산란되는 빛의 세기(Isc)와 파장(λ)과의 관계는?
- Isc= ∝ λ-1
- Isc= ∝ λ-2
- Isc= ∝ λ-3
- Isc= ∝ λ-4
74. 632nm 의 입사광에 대해 1/4파장판의 정상광선 굴절률이 1.538, 이상광선 굴절률이 1.549 일 때 1/4파장판의 최소 두께는 약 몇 mm 인가?
- 0.010
- 0.012
- 0.014
- 0.016
75. 다음 중 레이저를 이용하지 않는 것은?
- CD player
- 광통신
- 바코드 판독기
- 전자레인지
76. 선폭 Δv=4 × 102Hz인 레이저의 가간섭시간은 몇 초인가?
- 8.0×10-4
- 2.5×10-3
- 4.0×10-3
- 8.0×10-3
77. 네온 원자는 [3s2]상태에서 [2p4]상태로 천이할 때, 파장 632.8nm의 광을 방출하며, 천이율은 A24=606×106s-1이다. 이 때 방출된 광의 진폭수 폭은 약 몇 MHz 인가?
- 0.1
- 1
- 10
- 100
78. 가간섭거리(coherence length)에 대한 설명으로 적절하지 않은 것은?
- 가간섭거리는 스펙트럼 선폭에 반비례하다.
- 가간섭거리는 가간섭시간 동안 광파가 진공 속을 진행한 거리이다.
- 가간섭거리보다 긴 위상차를 가질 때 선명한 간섭 무늬를 얻을 수 있다.
- 일반 방전등에서 나온 광파의 가간섭거리보다 레이저 빛의 가간섭거리가 더 길다.
79. 다음 중 넓은 대역에 걸쳐 발진파장의 가변이 가능한 레이저는?
- Nd:YAG 레이저
- 반도체 레이저
- 구리 증기 레이저
- 색소 레이저
80. 어떤 레이저 광원의 발진주파수 대역폭이 4.5×108Hz로 주어질 때 가간섭거리(coherence length)는 몇 cm인가?
- 1.5
- 6.67
- 15
- 66.7







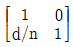
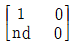
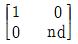
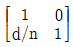
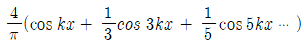
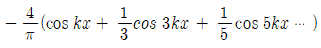
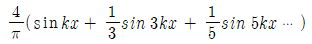
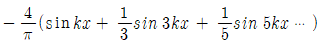
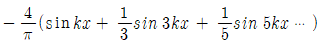 " 가 정답이다.
" 가 정답이다.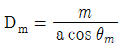
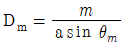
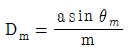
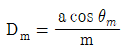
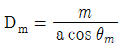 "이다.
"이다.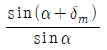
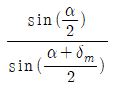

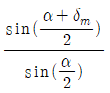
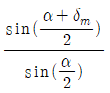 "이다.
"이다.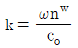 "은 제2고조파의 파수가 2배가 되어야 한다는 조건이다. 하지만 이는 위상정합조건이 아니라 주파수 조건이기 때문에 제2고조파 발생을 위한 위상정합조건이 아니다. 따라서 정답은 "
"은 제2고조파의 파수가 2배가 되어야 한다는 조건이다. 하지만 이는 위상정합조건이 아니라 주파수 조건이기 때문에 제2고조파 발생을 위한 위상정합조건이 아니다. 따라서 정답은 "