1과목: 응용역학
1. 그림과 같은 내민보에서 C점의 전단력(VC)과 휨모멘트(MC)는 각각 얼마인가?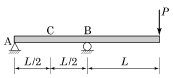
2. 트러스를 해석하기 위한 기본가정 중 옳지 않은 것은?
- 부재들은 마찰이 없는 힌지로 연결되어 있다.
- 부재 양단의 힌지 중심을 연결한 직선은 부재축과 일치한다.
- 모든 외력은 절점에 집중하중으로 작용한다.
- 하중 작용으로 인한 트러스 각 부재의 변형을 고려한다.
3. 그림과 같은 3힌지 라멘에 등분포하중이 작용할 경우 A점의 수평반력은?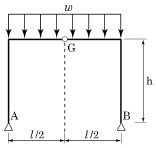
- 0

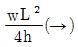
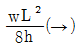
4. 일단고정 타단자유로 된 장주의 좌굴하중이 10tf일 때 양단힌지이고 기타 조건은 같은 장주의 좌굴하중은?
- 2.5tf
- 20tf
- 40tf
- 160tf
5. 그림과 같이 네 개의 힘이 평형 상태에 있다면 A점에 작용하는 힘 P와 AB사이의 거리 x는?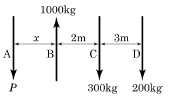
- P=400kgf, x=2.5m
- P=400kgf, x=3.6m
- P=500kgf, x=2.5m
- P=500kgf, x=3.2m
6. 그림에서 지점 C의 반력이 영(零)이 되기 위해 B점에 작용시킬 집중하중의 크기는?
- 8 tf
- 10 tf
- 12 tf
- 14 tf
7. 아래의 표에서 설명하는 것은?
- 제 1 공액보의 정리
- 제 2 공액보의 정리
- 제 1 모멘트면적 정리
- 제 2 모멘트면적 정리
8. 다음과 같은 단순보에서 최대 휨응력은? (단, 단면은 폭 40cm, 높이 50cm의 직사각형이다.)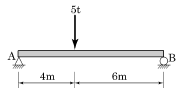
- 72kgf/cm2
- 87kgf/cm2
- 135kgf/cm2
- 150kgf/cm2
9. P=12tf 의 무게를 매달은 그림과 같은 구조물에서 T1이 받는 힘은?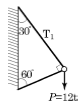
- 10.39tf(인장)
- 10.39tf(압축)
- 6tf(인장)
- 6tf(압축)
10. 다음 중 부정정 트러스를 해석하는 데 적합한 방법은?
- 모멘트 분배법
- 처짐각법
- 가상일의 원리
- 3연모멘트법
11. 경간 10m, 폭 20cm, 높이 30cm인 직사각형 단면의 단순보에서 전 경간에 등분포하중 w=2tf/m 가 작용할때 최대 전단응력은?
- 25kgf/cm2
- 30kgf/cm2
- 35kgf/cm2
- 40kgf/cm2
12. 단면적 A=20cm2, 길이 L=100cm인 강봉에 인장력 P=8t을 가하였더니 길이가 1cm 늘어났다. 이 강봉의 포아송수 m=3이라면 전단탄성계수 G는?
- 15000kg/cm2
- 45000kg/cm2
- 75000kg/cm2
- 95000kg/cm2
13. 다음 그림과 같이 직교좌표계 위에 있는 사다리꼴 도형 OABC 도심의 좌표( 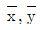 )는? (단, 좌 단위는cm)
)는? (단, 좌 단위는cm)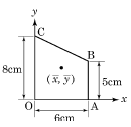
- (2.54, 3.46)
- (2.77, 3.31)
- (3.34, 3.21)
- (3.54, 2.74)
14. “여러 힘의 모멘트는 그 합력의 모멘트와 같다.”라는 것은 무슨 원리인가?
- 가상(假想)일의 원리
- 모멘트 분배법
- Varignon의 원리
- 모어(Mohr)의 정리
15. 경간 5m, 높이 30cm, 폭 20cm의 단면을 갖는 단순보에 등분포하중 W=400kgf/m가 만재하여 있을 때 최대 처짐은? (단, E=1×105kgf/cm2)
- 4.71cm
- 2.67cm
- 1.27cm
- 0.72cm
16. 다음 인장부재의 변위를 구하는 식으로 옳은 것은? (단, 단면적은 A, 탄성계수는 E)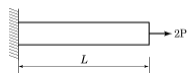
- PL/EA
- 2PL/EA
- 3PL/EA
- 4PL/EA
17. 그림과 같은 1차 부정정 구조물의 A지점의 반력은? (단, EI는 일정하다.)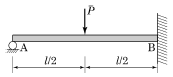
- 5P/16
- 11P/16
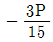
- 5P/32
18. 폭 12cm, 높이 20cm인 직사각형 단면의 최소 회전반지름 r은?
- 5.81cm
- 3.46cm
- 6.92cm
- 7.35cm
19. 그림과 같은 단주에서 편심거리 e에 P=30tf 가 작용할 때 단면에 인장력이 생기지 않기 위한 의 한계는?
- 3.3cm
- 5cm
- 6.7cm
- 10cm
20. 그림과 같은 연속보 B점의 휨모멘트 MB는?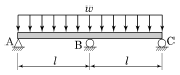
2과목: 측량학
21. 사진측량의 특징에 대한 설명으로 옳지 않은 것은?
- 기상의 영향을 받지 않고 전천후 측량을 수행할 수 있다.
- 광범위한 지역에 대한 동시 측량이 가능하다.
- 정성적 측량이 가능하다.
- 축척 변경이 용이하다.
22. 촬영고도 3,000m에서 초점거리 15cm의 카메라로 평지를 촬영한 밀착사진의 크기가 23cm×23cm이고 종중복도가 57%, 횡중복도가 30%일 때 이 연직사진의 유효 모델 면적은?
- 5.4km2
- 6.4km2
- 7.4km2
- 8.4km2
23. 교점(I.P.)의 위치가 기점으로부터 143.25m일 때 곡선반지름 150m, 교각 58°14′24″인 단곡선을 설치하고자 한다면 곡선시점의 위치는? (단, 중심말뚝 간격20m)
- No.2 + 3.25
- No.2 + 19.69
- No.3 + 9.69
- No.4 + 3.56
24. 평균유속 관측방법 중 3점법을 사용하기 위한 관측유속으로 짝지어진 것은? (단, h는 전체 수심)
- 수면에서 0.1h, 0.4h, 0.9h 지점의 유속
- 수면에서 0.1h, 0.4h, 0.8h 지점의 유속
- 수면에서 0.2h, 0.4h, 0.8h 지점의 유속
- 수면에서 0.2h, 0.6h, 0.8h 지점의 유속
25. 완화곡선 중 주로 고속도로에 사용되는 것은?
- 3차 포물선
- 클로소이드(clothoid) 곡선
- 반파장 싸인(sine) 체감곡선
- 렘니스케이트(lemniscate) 곡선
26. 등고선에 관한 설명으로 틀린 것은?
- 간곡선은 계곡선보다 가는 실선으로 나타낸다.
- 주곡선 간격이 10m이면 간곡선 간격은 5m이다.
- 계곡선은 주곡선보다 굵은 실선으로 나타낸다.
- 계곡선 간격은 주곡선 간격의 5배이다.
27. 원곡선에서 장현 L과 그 중앙 종거 M을 관측하여 반지름 R을 구하는 식으로 옳은 것은?
- L2/8M
- L2/4M
- L2/2M
- L2/M
28. 폐합다각측량에서 각 관측보다 거리 관측 정밀도가 높을 때 오차를 배분하는 방법으로 옳은 것은?
- 해당 측선 길이에 비례하여 배분한다.
- 해당 측선 길이에 반비례하여 배분한다.
- 해당 측선의 위, 경거의 크기에 비례하여 배분한다.
- 해당 측선의 위, 경거의 크기에 반비례하여 배분한다.
29. 어떤 측선의 길이를 3군으로 나누어 관측하여 표와 같은 결과를 얻었을 때, 측선 길이의 최확값은?
- 100.344m
- 100.346m
- 100.348m
- 100.350m
30. 수준측량에서 전시와 후시의 거리를 같게 하여도 제거되지 않는 오차는?
- 시준선과 기포관축이 평행하지 않을 때 생기는 오차
- 표척 눈금의 읽음오차
- 광선의 굴절오차
- 지구곡률 오차
31. 그림과 같이 A점에서 B점에 대하여 장애물이 있어 시준을 못하고 B′점을 시준하였다. 이때 B점의 방향각 TB 를 구하기 위한 보정각(x)을 구하는 식으로 옳은것은? (단, e <1.0m, p=206265, S=4km)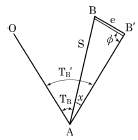
32. 지형도를 작성할 때 지형 표현을 위한 원칙과 거리가 먼 것은?
- 기복을 알기 쉽게 할 것
- 표현을 간결하게 할 것
- 정량적 계획을 엄밀하게 할 것
- 기호 및 도식을 많이 넣어 세밀하게 할 것
33. 축척 1:1200 지형도 상에서 면적을 측정하는데 축척을 1:1000으로 잘못 알고 면적을 산출한 결과 1200m2를 얻었다면 정확한 면적은?(오류 신고가 접수된 문제입니다. 반드시 정답과 해설을 확인하시기 바랍니다.)
- 8,333m2
- 12,368m2
- 15,806m2
- 17,280m2
34. A점에서 출발하여 다시 A점에 되돌아오는 다각측량을 실시하여 위거오차 20cm, 경거오차 30cm가 발생하였다. 전 측선길이가 800m일 때 다각측량의 정밀도는?
- 1/1000
- 1/1730
- 1/2220
- 1/2630
35. 평판을 설치할 때 고려하여야 할 조건과 거리가 먼 것은?
- 수평 맞추기
- 교회 맞추기
- 중심 맞추기
- 방향 맞추기
36. 철도에 완화곡선을 설치하고자 할 때 캔트(cant)의 크기 결정과 직접적인 관계가 없은 것은?
- 레일간격
- 곡선반지름
- 원곡선의 교각
- 주행속도
37. 삼각측량에서 B점의 좌표 XB=50.000m, YB=200.000m, BC의 길이 25.478m, BC의 방위각 77°11′56″일 때 C점의 좌표는?
- XC=55.645m, YC=175.155m
- XC=55.645m, YC=224.845m
- XC=74.845m, YC=194.355m
- XC=74.845m, YC=205.645m
38. 그림에서 B점의 지반고는? (단, HA=39.695m)
- 39.405m
- 39.985m
- 42.985m
- 46.305m
39. 경중률에 대한 설명으로 틀린 것은?
- 관측횟수에 비례한다.
- 관측거리에 반비례한다.
- 관측값의 오차에 비례한다.
- 사용기계의 정밀도에 비례한다.
40. 기초터파기 공사를 하기 위해 가로, 세로, 깊이를 줄자로 관측하여 다음과 같은 결과를 얻었다. 토공량과 여기에 포함된 오차는?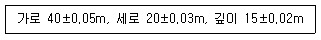
- 6,000±28.4m3
- 6,000±48.9m3
- 12,000±28.4m3
- 12,000±48.9m3
3과목: 수리학
41. 직경 20cm인 원형 오리피스로 0.1m3/s의 유량을 유출시키려 할 때 필요한 수심(오리피스 중심으로부터 수면까지의 높이)은? (단, 유량계수 c = 0.6)
- 1.24m
- 1.44m
- 1.56m
- 2.00m
42. 등류의 마찰속도 u*를 구하는 공식으로 옳은 것은? (단, H : 수심, I : 수면경사, g : 중력가속도)
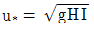
- u*=gHI
- u*=gH2I
- u*=gHI2
43. 2초에 10m를 흐르는 물의 속도수두는?
- 1.18m
- 1.28m
- 1.38m
- 1.48m
44. 개수로에 대한 설명으로 옳은 것은?
- 동수경사선과 에너지경사선은 항상 평행하다.
- 에너지경사선은 자유수면과 일치한다.
- 동수경사선은 에너지경사선과 항상 일치한다.
- 동수경사선과 자유수면은 일치한다.
45. 그림과 같이 지름 3m, 길이 8m인 수문에 작용하는 수평분력의 작용점까지 수심(hc)은?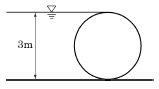
- 2.00m
- 2.12m
- 2.34m
- 2.43m
46. 유량 147.6L/s를 송수하기 위하여 내경 0.4m의 관을 700m 설치하였을 때의 관로 경사는? (단, 조도계수 n=0.012, Manning공식 적용)
- 3/700
- 2/700
- 3/500
- 2/500
47. 정수압의 성질에 대한 설명으로 옳지 않은 것은?
- 정수압은 수중의 가상면에 항상 직각방향으로 존재한다.
- 대기압을 압력의 기준(0)으로 잡은 정수압은 반드시 절대압력으로 표시된다.
- 정수압의 강도는 단위면적에 작용하는 압력의 크기로 표시한다.
- 정수 중의 한 점에 작용하는 수압의 크기는 모든 방향에서 같은 크기를 갖는다.
48. 레이놀즈수가 갖는 물리적인 의미는?
- 점성력에 대한 중력의 비(중력/점성력)
- 관성력에 대한 중력의 비(중력/관성력)
- 점성력에 대한 관성력의 비(관성력/점성력)
- 관성력에 대한 점성력의 비(점성력/관성력)
49. 관망 문제해석에서 손실수두를 유량의 함수로 표시하여 사용할 경우 지름 D인 원형단면관에 대하여 hL=kQ2으로 표시할 수 있다. 관의 특성 제원에 따라 결정되는 상수 k의 값은? (단, f는 마찰손실계수이고, ℓ은 관의 길이이며 다른 손실은 무시함)
50. 지름이 20cm인 A관에서 지름이 10cm인 B관으로 축소되었다가 다시 지름이 15cm인 C관으로 단면이 변화되었다. B관의 평균유속이 3m/s일 때 A관과 C관의 유속은? (단, 유체는 비압축성이며, 에너지 손실은 무시한다.)
- A관의 VA=0.75m/s, C관의 VC=2.00m/s
- A관의 VA=1.50m/s, C관의 VC=1.33m/s
- A관의 VA=0.75m/s, C관의 VC=1.33m/s
- A관의 VA=1.50m/s, C관의 VC=0.75m/s
51. 한계 후루드수(Froude number)를 사용하여 구분할수 있는 흐름 특성은?
- 등류와 부등류
- 정류와 부정류
- 층류와 난류
- 상류와 사류
52. 대수층의 두께 2m, 폭 1.2m이고 지하수 흐름의 상‧하류 두 점 사이의 수두차는 1.5m, 두 점 사이의 평균거리 300m, 지하수 유량이 2.4m3/d일 때 투수계수는?
- 200m/d
- 225m/d
- 267m/d
- 360m/d
53. 단면적 2.5cm2, 길이 1.5m인 강철봉이 공기중에서 무게가 28N이었다면 물(비중=1.0) 속에서 강철봉의 무게는?
- 2.37N
- 2.43N
- 23.72N
- 24.32N
54. 물의 성질에 대한 설명으로 옳지 않은 것은? (단, Cw: 물의 압축률, Ew : 물의 체적탄성률, 0℃에서의 일정한 수온 상태)
- 물의 압축률이란 압력변화에 대한 부피의 감소율을 단위부피당으로 나타낸 것이다.
- 기압이 증가함에 따라 Ew는 감소하고 Cw는 증가한다.
- Cw와 Ew의 상관식은 Cw=1/Ew이다.
- Ew는 Cw값보다 대단히 크다.
55. 뉴턴유체(Newtonian fluid)에 대한 설명으로 옳은 것은?
- 전단속도 (dv/dy)의 크기에 따라 선형으로 점도가 변한다.
- 전단응력(τ)과 전단속도 (dv/dy)의 관계는 원점을 지나는 직선이다.
- 물이나 공기 등 보통의 유체는 비뉴턴유체이다.
- 유체가 압력의 변화에 따라 밀도의 변화를 무시할 수 없는 상태가 된 유체를 의미한다.
56. 지름 20cm, 길이가 100m인 관수로 흐름에서 손실수두가 0.2m라면 유속은? (단, 마찰손실 계수 f=0.03이다.)
- 0.61m/s
- 0.57m/s
- 0.51m/s
- 0.48m/s
57. 한계수심 hc와 비에너지 he와의 관계로 옳은 것은? (단, 광폭직사각형 단면인 경우)

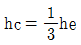
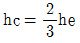
- hc=2he
58. 굴착정의 유량 공식으로 옳은 것은? (여기서 C : 피압대수층의 두께, K : 투수계수, h : 압력수면의 높이, h0 : 우물안의 수심, R : 영향원의 반지름, r0 : 우물의 반지름)
59. 다음 설명 중 옳지 않은 것은?
- 베르누이 정리는 에너지 보존의 법칙을 의미한다.
- 연속 방정식은 질량보존의 법칙을 의미한다.
- 부정류(unsteady flow)란 시간에 대한 변화가 없는 흐름이다.
- Darcy법칙의 적용은 레이놀즈수에 대한 제한을 받는다.
60. 4각 위어 유량(Q)과 수심(h)의 관계가 Q∝h3/2일 때, 3각 위어의 유량(Q)과 수심(h)의 관계로 옳은 것은?
- Q∝h1/2
- Q∝h3/2
- Q∝h2
- Q∝h5/2
4과목: 철근콘크리트 및 강구조
61. fck=24MPa, fy=300MPa, bω=400mm, d=500mm인 직사각형 철근콘크리트보에서 콘크리트가 부담하는 공칭 전단강도(Vc)는 얼마인가?
- 105.7kN
- 110.1kN
- 142.7kN
- 163.3kN
62. 다음 중 용접이음을 한 경우 용접부의 결함을 나타내는 용어가 아닌 것은?
- 언더컷(undercut)
- 필렛(fillet)
- 크랙(crack)
- 오버랩(overlap)
63. 강도 설계법에서 1방향 슬래브(slab)의 구조세목에 관한 사항 중 틀린 것은?
- 1방향 슬래브의 두께는 최소 100mm이상이어야 한다.
- 슬래브의 정모멘트 철근 및 부모멘트 철근의 중심 간격은 위험단면에서는 슬래브 두께의 2배이하이어야하고, 또한 300mm 이하로 하여야 한다.
- 슬래브의 정모멘트 철근 및 부모멘트 철근의 중심간격은 위험단면 이외의 단면에서는 슬래브 두께의 3배이하이어야 하고, 또한 600mm 이하로 하여야 한다.
- 1방향 슬래브에서는 정모멘트 철근 및 부모멘트 철근에 직각방향으로 수축ㆍ온도철근을 배치하여야 한다.
64. 강도설계법에서 전단 보강 철근의 공칭전단강도 Vs가 (2√fck/3)bωd 를 초과하는 경우에 대한 설명으로 옳은 것은?
- 전단철근을 d/4이하, 600mm 이하로 배치해야 한다.
- 전단철근을 d/2이하, 300mm 이하로 배치해야 한다.
- 전단철근을 d/4이하, 300mm 이하로 배치해야 한다.
- bωd의 단면을 변경하여야 한다.
65. 다음 중'피복두께'에 대한 설명으로 적합한 것은?
- 콘크리트 표면과 그에 가장 가까이 배치된 주철근 표면 사이의 콘크리트 두께
- 콘크리트 표면과 그에 가장 가까이 배치된 부철근 표면 사이의 콘크리트 두께
- 콘크리트 표면과 그에 가장 가까이 배치된 가외철근 표면 사이의 콘크리트 두께
- 콘크리트 표면과 그에 가장 가까이 배치된 철근 표면 사이의 콘크리트 두께
66. 철근의 간격제한에 대한 설명으로 틀린 것은?
- 동일평면에서 평행한 철근 사이의 수평 순간격은 25mm 이상, 철근의 공칭지름이상으로 하여야 한다.
- 상단과 하단에 2단 이상으로 배치된 경우 상하 철근은 동일연직면 내에 배치되어야 하고, 이때 상하 철근의 순간격은 25mm 이상으로 하여야 한다.
- 나선철근 또는 띠철근이 배근된 압축부재에서 축방향 철근의 순간격은 40mm이상, 또한 철근 공칭지름의 1.5배 이상으로 하여야 한다.
- 벽체 또는 슬래브에서 휨 주철근의 간격은 벽체나 슬래브 두께의 5배 이하로 하여야 하고, 또한 800mm이하로 하여야 한다.
67. 강도설계법으로 철근콘크리트 부재의 설계시에 사용되는 강도감소계수가 잘못된 것은?
- 인장지배단면 : 0.85
- 전단력을 받는 부재 : 0.70
- 무근 콘크리트의 휨모멘트 : 0.55
- 압축지배 단면 중 나선 철근으로 보강된 철근콘크리트 부재 : 0.70
68. 보의 휨파괴에 대한 설명 중 틀린 것은?
- 과소철근보는 철근이 먼저 항복하게 되지만 철근은 연성이 크기 때문에 파괴는 단계적으로 일어난다.
- 과다철근보는 철근량이 많기 때문에 더욱 느린 속도로 파괴되고 위험예측이 가능하다.
- 인장철근이 항복강도 fy에 도달함과 동시에 콘크리트도 극한변형률에 도달하여 파괴되는 보를 균형철근보라 한다.
- 인장으로 인한 파괴 시 중립축은 위로 이동한다.
69. 단면이 300×500mm이고, 150mm2의 PS 강선 6개를 강선군의 도심과 부재단면의 도심축이 일치하도록 배치된 프리텐션 PC 부재가 있다. 강선의 초기 긴장력이 1,000MPa일 때 콘크리트의 탄성변형에 의한 프리스트레스의 감소량은? (단, n=6)
- 36MPa
- 30MPa
- 6MPa
- 4.8MPa
70. 다음 그림과 같은 직사각형 단철근 보에서 강도 설계법을 사용할 때 콘크리트의 등가직사각형 응력블록의 깊이(a)는 얼마인가? (단, fck=21MPa, fy=300MPa)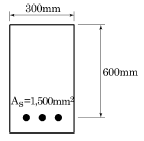
- 84mm
- 102mm
- 153mm
- 200mm
71. 보통 강재의 용접에서 용접봉을 사용할 경우 용접자세에 대하여 적당한 것은?
- 상향 용접자세
- 하향 용접자세
- 횡방향 용접자세
- 눈높이와 같은 자세
72. fck=24MPa, fy=300MPa일 때 다음 그림과 같은 보의 균형 철근량은?(2022년 변경된 규정 적용됨)
- 5,254mm2
- 5,842mm2
- 6,732mm2
- 7,254mm2
73. 깊은 보는 주로 어느 작용에 의하여 전단력에 저항 하는가?
- 장부작용(dowel action)
- 골재 맞물림(aggregate interaction)
- 전단마찰(shear friction)
- 아치작용(arch action)
74. 복철근 단면으로 설계해야 할 경우를 설명한 것으로 틀린 것은?
- 경제성을 우선적으로 고려해야 할 경우
- 정(+), 부(-)의 모멘트를 번갈아 받는 구조의 경우
- 처짐의 증가를 방지해야 할 경우
- 구조상의 사정으로 보의 높이가 제한을 받는 경우
75. 다음 중 일반적인 철근의 정착 방법 종류가 아닌 것은?
- 묻힘길이에 의한 정착
- 갈고리에 의한 정착
- 약품에 의한 정착
- 철근의 가로 방향에 T형이 되도록 철근을 용접해 붙이는 정착
76. bw=300mm, d=500mm이고, As=3-D25(=1,520mm2)가 1열로 배치된 단철근 직사각형 단면의 설계휨강도(øMn)는? (단, fck=24MPa, fy=400MPa이고, 이 단면은 인장지배단면이다.)
- 207.9kN∙m
- 232.7kN∙m
- 256.2kN∙m
- 294.8kN∙m
77. bw=300mm, d=400mm, As=2,400mm2, As′1,200mm2인 복철근 직사각형단면의 보에서 하중이 작용할 경우 탄성처짐량이 1.5mm였다. 5년 후 총 처짐량은 얼마인가?
- 2.0mm
- 2.5mm
- 3.0mm
- 3.5mm
78. PSC 부재의 프리스트레스 감소원인 중 프리스트레스를 도입한 후 시간의 경과에 의해 발생하는 것은?
- PS강재의 릴랙세이션으로 인한 손실
- PS강재와 쉬스의 마찰로 인한 손실
- 정착장치의 활동으로 인한 손실
- 콘크리트의 탄성변형으로 인한 손실
79. D-25(공칭직경 : 25.4mm)를 사용하는 압축이형철근의 기본정착길이는? (단, fck=30MPa, fy=400MPa이다.)
- 413mm
- 447mm
- 464mm
- 487mm
80. 그림과 같이 경간 20m인 PSC 보가 프리스트레스힘(P) 1000kN을 받고 있을 때 중앙단면에서의 상향력(U)을 구하면?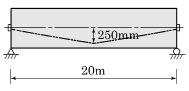
- 30kN
- 40kN
- 50kN
- 60kN
5과목: 토질 및 기초
81. 흙의 투수계수에 관한 설명으로 틀린 것은?
- 흙의 투수계수는 흙 유효입경의 제곱에 비례한다.
- 흙의 투수계수는 물의 점성계수에 비례한다.
- 흙의 투수계수는 물의 단위중량에 비례한다.
- 흙의 투수계수는 형상계수에 따라 변화한다.
82. 어떤 흙의 비중이 2.65, 간극률이 36%일 때 다음 중 분사현상이 일어나지 않을 동수경사는?
- 1.9
- 1.2
- 1.1
- 0.9
83. 어떤 퇴적지반의 수평방향의 투수계수가 4.0×10-3cm/s이고, 수직방향의 투수계수가 3.0×10-3cm/s일 때 등가투수계수는 얼마인가?
- 3.46×10-3cm/s
- 5.0×10-3cm/s
- 6.0×10-3cm/s
- 6.93×10-3cm/s
84. 현장 토질조사를 위하여 베인 테스트(Vane Test)를 행하는 경우가 종종 있다. 이 시험은 다음 중 어느 경우에 많이 쓰이는가?
- 연약한 점토의 점착력을 알기 위해서
- 모래질 흙의 다짐도를 측정하기 위해서
- 모래질 흙의 내부마찰각을 알기 위해서
- 모래질 흙의 투수계수를 측정하기 위하여
85. 어떤 흙의 중량이 450g이고 함수비가 20%인 경우이 흙을 완전히 건조시켰을 때 중량은 얼마인가?
- 360g
- 425g
- 400g
- 375g
86. 유효입경이 0.1mm이고 통과벽분율 80%에 대응하는 입경이 0.5mm, 60%에 대응하는 입경이 0.4mm, 40%에 대응하는 입경이 0.3mm, 20%에 대응하는 입경이 0.2mm일때 이 흙의 균등계수는?
- 2
- 3
- 4
- 5
87. 흙의 다짐 시험에 대한 설명으로 옳은 것은?
- 다짐에너지가 크면 최적함수비가 크다.
- 다짐에너지와 관계없이 최대건조단위중량은 일정하다.
- 다짐에너지와 관계없이 최적함수비는 일정하다.
- 몰드 속에 있는 흙의 함수비는 다짐에너지에 거의 영향을 받지 않는다.
88. 지표면이 수평이고 옹벽의 뒷면과 흙과의 마찰각이 0인 연직옹벽에서 Coulomb의 토압과 Rankine의 토압은 어떻게 되는가?
- Coulomb의 토압은 항상 Rankine의 토압보다 크다.
- Coulomb의 토압은 Rankine의 토압보다 클 때도 있고, 작을 때도 있다.
- Coulomb의 토압과 Rankine의 토압은 같다.
- Coulomb의 토압은 항상 Rankine의 토압보다 작다.
89. 연약지반에 말뚝을 시공한 후, 부의 주면마찰력이 발생되면 말뚝의 지지력은?
- 증가된다.
- 감소된다.
- 변함이 없다.
- 증가할 수도 있고 감소할 수도 있다.
90. 말뚝의 분류 중 지지상태에 따른 분류에 속하지 않는 것은?
- 다짐 말뚝
- 마찰 말뚝
- Pedestal 말뚝
- 선단 지지 말뚝
91. 다음 중 표준관입시험으로부터 추정하기 어려운 항목은?
- 극한지지력
- 상대밀도
- 점성토의 연경도
- 투수성
92. 흙댐에서 수위가 급강하한 경우 사면안정해석을 위한 강도정수 값을 구하기 위하여 어떠한 조건의 삼축압축시험을 하여야 하는가?
- Ouick 시험
- CD 시험
- CU 시험
- UU 시험
93. 단위중량이 1.6t/m3인 연약지반(ø=0°) 지반에서 연직으로 2m까지 보강 없이 절취할 수 있다고 한다. 이 점토지반의 점착력은?
- 0.4t/m2
- 0.8t/m2
- 1.4t/m2
- 1.8t/m2
94. 어떤 점토시료를 일축압축 시험한 결과 수평면과 파괴면이 이루는 각이 48°였다. 점토 시료의 내부마찰각은?
- 3°
- 6°
- 18°
- 30°
95. 어떤 점토의 액성한계 값이 40%이다. 이 점토의 불교란 상태의 압축지수 Cc를 Skempton 공식으로 구하면 얼마인가?
- 0.27
- 0.29
- 0.36
- 0.40
96. 어떤 흙의 최대 및 최소 건조단위중량이 1.8t/m3과 1.6t/m3이다. 현장에서 이 흙의 상대밀도(relative density)가 60%라면 이 시료의 현장 상대다짐도(relative compaction)는?
- 82%
- 87%
- 91%
- 95%
97. 자연 상태 흙의 일축압축강도가 0.5kg/cm2고 이 흙을 교란시켜 일축압축강도 시험을 하니 강도가 0.1kg/cm2이었다. 이 흙의 예민비는 얼마인가?
- 50
- 10
- 5
- 1
98. 직경 30cm의 평판을 이용하여 점토위에서 평판재하시험을 실시하고 극한지지력 15t/m2를 얻었다고 할 때 직경이 2m인 원형기초의 총허용하중을 구하면? (단, 안전율은 3을 적용한다.)
- 8.3ton
- 15.7ton
- 24.2ton
- 32.6ton
99. 지표면에 집중하중이 작용할 때, 연직응력에 관한 다음 사항 중 옳은 것은? (단, Boussinesq 이론을 사용, E는 Young계수이다.)
- E에 무관하다.
- E에 정비례한다.
- E의 제곱에 정비례한다.
- E의 제곱에 반비례한다.
100. 2t의 무게를 가진 낙추로서 낙하고 2m로 말뚝을 박을 때 최종적으로 1회 타격당 말뚝의 침하량이 20mm였다. Sander 공식에 의하면 이때 말뚝의 허용지지력은?
- 10t
- 20t
- 67t
- 25t
6과목: 상하수도공학
101. 펌프의 임펠러 입구에서 정압이 그 수온에 상당하는 포화 증기압 이하가 되면 그 부분의 물이 증발해서 공동이 생기거나 흡입관으로부터 공기가 흡입되어 공동이 생기는 현상은?
- Characteristic Curves
- Specific Speed
- Positive Head
- Cavitation
102. 상수의 응집침전에서 응집제의 주입률을 시험하는 시험법은?
- Sedimentation test
- Coulmn test
- Water quality test
- Jar test
103. 활성슬러지법 중 아래와 같은 특징을 갖는 방법은?
- 계단식 포기법
- 심층 포기법
- 장기 포기법
- 산화구법
104. 하천의 자정작용 중에서 가장 큰 작용을 하는 것은?
- 침전
- 투과
- 화학적 작용
- 생물학적 작용
105. 하수처리장 부지선정에 관한 설명으로 옳지 않은 것은?
- 홍수로 인한 침수 위험이 없어야 한다.
- 방류수가 충분히 회석, 혼합되어야 하며 상수도 수원 등에 오염되지 않는 곳을 선택한다.
- 처리장의 부지는 장래 확장을 고려해서 넓게 하며 주거 및 상업지구에 인접한 곳이어야 한다.
- 오수 또는 폐수가 하수처리장까지 가급적 자연유하식으로 유입하고 또한 자연유하로 방류하는 곳이 좋다.
106. Talbot 공식의 a(분자상수) 값이 1800, b(분모상수) 값이 15일 때, 지속시간 15분에 대한 강우강도는?
- 2.64 mm/h
- 9.92 mm/h
- 10.67 mm/h
- 60.00 mm/h
107. 하수관거가 갖추어야 할 특성에 대한 설명으로 옳지 않은 것은?
- 외압에 대한 강도가 충분하고 파괴에 대한 저항이 커야 한다.
- 유량의 변동에 대해서 유속의 변동이 큰 수리특성을 지닌 단면형이 좋다.
- 산 및 알칼리의 부식성에 대해서 강해야 한다.
- 이음의 시공이 용이하고, 그 수밀성과 신축성이 높아야 한다.
108. 우수조정지를 설치하는 위치로서 적절하지 않은 것은?
- 오수발생량이 많은 곳
- 하류관거 유하능력이 부족한 곳
- 방류수로 유하능력이 부족한 곳
- 하류지역 펌프장 능력이 부족한 곳
109. 다음 중 맛과 냄새의 제거에 주로 사용되는 것은?
- PAC(고분자 응집제)
- 황산반토
- 활성탄
- CuSO4
110. 하수관거의 유속 및 경사에 대한 설명으로 옳지 않은 것은?
- 유속은 일반적으로 하류로 유하함에 따라 점차 크게한다.
- 경사는 하류로 감에 따라 점차 작아지도록 한다.
- 유속이 느리면 관거의 바닥에 오물이 침전하여 세척비 등 유지관리비가 많이 든다.
- 유속이 빠르면 관거 손상의 우려가 작아지므로 내용년수가 길어진다.
111. 분류식 하수관거 계통(separated system)의 특징에 대한 설명으로 옳지 않은 것은?
- 오수는 처리장으로 도달, 처리된다.
- 우수관과 오수관이 잘못 연결될 가능성이 있다.
- 관거매설비가 큰 것이 단점이다.
- 강우시 오수가 처리되지 않은 채 방류되는 단점이 있다.
112. 취수시설을 선정할 때 수원(水源)이 하천, 호소, 댐(저수지)인 경우에 적용할 수 있으며 보통 대량 취수에 적합하고 비교적 안정된 취수가 가능한 것은?
- 취수탑
- 깊은 우물
- 취수틀
- 취수관거
113. 5,000m3/d의 화학 침전 처리수를 여과지에서 여과속도 5m3/m2∙ h로 여과하고 있다. 역세척은 1일 8회, 1회 역세척 시간은 15분일 경우 1지에 소요되는 이론적인 여과 면적은? (단, 여과지 수는 5지이다.)
- 8.333 m2
- 9.091 m2
- 20.647 m2
- 41.667 m2
114. 슬러지 반송비가 0.4, 반송슬러지의 농도가 1%일 때 포기조 내의 MLSS 농도는?
- 1,234mg/L
- 2,857mg/L
- 3,325mg/L
- 4,023mg/L
115. 급수방식을 직결식과 저수조식으로 구분할 때, 저수조식의 적용이 바람직한 경우가 아닌 것은?
- 일시에 다량의 물을 사용하거나 사용수량의 변동이 클 경우
- 배수관의 수압이 급수장치의 사용수량에 대하여 충분한 경우
- 배수관의 압력변동에 관계없이 상시 일정한 수량과 압력을 필요로 하는 경우
- 재해시나 사고 등에 의한 수도의 단수나 감수시에도 물을 반드시 확보해야 할 경우
116. 하천에 오염원 투여시 시간 또는 거리에 따른 오염지표(BOD, DO, N)와 미생물의 변화 4단계(Whipple의 4단계)의 순서로 옳은 것은?
- ㉠ - ㉡ - ㉢ - ㉣
- ㉠ - ㉢ - ㉡ - ㉣
- ㉡ - ㉠ - ㉢ - ㉣
- ㉡ - ㉢ - ㉠ - ㉣
117. 계획오수량 산정방법에 대한 설명으로 틀린 것은?
- 생활오수량의 1인1일 최대오수량은 상수도계획상의 1인1일 최대급수량을 감안하여 결정한다.
- 지하수량은 1인1일 평균오수량의 5~10%로 한다.
- 계획시간 최대오수량은 계획1일 최대오수량의 1시간당 수량의 1.3~1.8배를 표준으로 한다.
- 합류식에서 우천시 계획오수량은 원칙적으로 계획시간 최대오수량의 3배 이상으로 한다.
118. 펌프에 대한 설명으로 틀린 것은?
- 수격현상은 펌프의 급정지시 발생한다.
- 손실수두가 작을수록 실양정은 전양정과 비슷해진다.
- 비속도(비교회전도)가 클수록 같은 시간에 많은 물을 송수할 수 있다.
- 흡입구경은 토출량과 흡입구의 유속에 의해 결정된다.
119. 처리수량이 5,000m3/d인 정수장에서 8mg/L의 농도로 염소를 주입하였다. 잔류염소농도가 0.3mg/L이었다면 염소요구량은? (단, 염소의 순도는 75%이다.)
- 38.5kg/d
- 51.3kg/d
- 63.3kg/d
- 69.5kg/d
120. 계획급수량에 대한 설명으로 옳지 않은 것은?
- 계획1일 평균급수량은 계획1일 최대급수량의 50%이다.
- 계획1일 최대급수량은 계획1일 평균급수량 × 계획첨두율로 나타낼 수 있다.
- 계획1일 평균급수량은 계획1인 평균급수량 × 계획급수인구로 나타낼 수 있다.
- 계획1일 최대급수량을 구하기 위한 첨두율은 소규모의 도시일수록 급수량의 변동폭이 커서 값이 커진다.





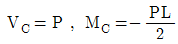
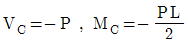
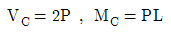
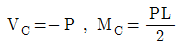

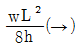 "이다.
"이다.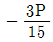 "이다.
"이다.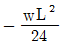

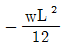
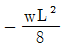
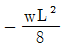 "이다.
"이다.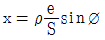
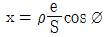
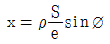

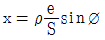 "
"
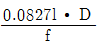
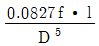
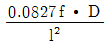
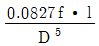 "입니다.
"입니다.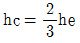 "
"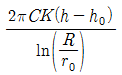
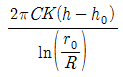
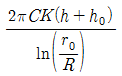
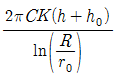
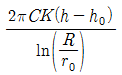 " 입니다.
" 입니다.
MC = 10 kN·m (내민보의 중심점에서 휨모멘트는 최대값인 10 kN·m이다.)
정답이 "