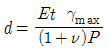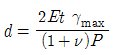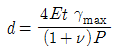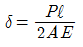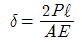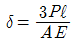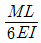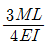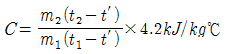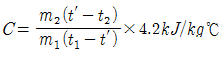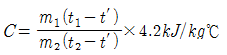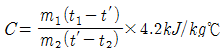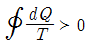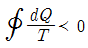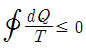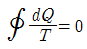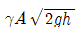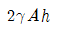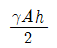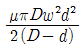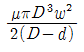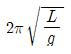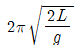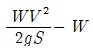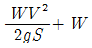1과목: 재료역학
1. 지름 9㎝인 원형단면을 직사각형 단면 b×h로 잘라내어 최대강도를 갖도록 할 때 단면치수 b와 h는 몇 ㎝인가?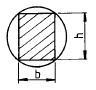
- b=√36 , h=√64
- b=√27 , h=√54
- b=√42 , h=√42
- b=√25 , h=√60
- 단면의 최대강도는 단면의 모멘트 of inertia (I)가 최대일 때 나타납니다. 원형단면의 모멘트 of inertia는 (π/4)×r^4이고, 직사각형 단면의 모멘트 of inertia는 (b×h^3)/12입니다. 따라서, 원형단면에서 직사각형 단면을 잘라내어 모멘트 of inertia를 최대로 만들기 위해서는, 원형단면의 지름을 b와 h로 나누어야 합니다. 이렇게 나누었을 때, b:h의 비율은 1:√3입니다. 따라서, b와 h의 길이는 각각 √27과 √54가 됩니다.
2. 비틀림 모멘트 T, 극관성 모멘트를 IP, 축의 길이를 L, 전단탄성계수를 G 라 할 때, 단위 길이당 비틀림각은?
- TG/IP
- T/GIP
- L2/IP
- T/IP
- 단위 길이당 비틀림각은 비틀림 모멘트 T를 극관성 모멘트 IP와 전단탄성계수 G의 곱으로 나눈 값이다. 이는 비틀림 모멘트 T가 단위 길이당 비틀림각에 미치는 영향을 나타내는 비례상수이며, 극관성 모멘트 IP는 단면의 형상과 크기에 따라 달라지는 상수이다. 따라서 단위 길이당 비틀림각은 T/GIP이다.
3. 최대 굽힘모멘트 8 kN∙m 를 받는 원형단면의 굽힘응력을 60 MPa로 하려면 지름을 약 몇 cm로 해야 하는가?
- 1.11
- 11.1
- 3.01
- 30.1
- 원형단면의 굽힘모멘트는 M = (π/32) * σ * d^3 이다. 여기서 M = 8 kN∙m = 8000 N∙m, σ = 60 MPa = 60 N/mm^2 이므로,
8000 = (π/32) * 60 * d^3
d^3 = (8000 * 32) / (π * 60) = 136.53
d = 5.5 cm (약)
따라서, 지름은 약 11.1 cm 이다.
4. 다음 그림의 등분포 하중의 단순지지보에서 A의 보가 B의 보 보다 최대처짐이 몇 배나 되는가?
- 4
- 8
- 12
- 16
- 등분포 하중의 최대처짐은 wL^3/48EI 이다. A의 보와 B의 보의 길이는 같으므로 L은 같다. E와 I는 재료와 단면에 따라 일정하므로 w가 가장 큰 보가 최대처짐이 가장 커진다. 따라서 w가 16인 B의 보가 w가 2배 작은 A의 보보다 최대처짐이 2^3=8배 크다.
정답이 "8"인 이유는 w가 16인 B의 보가 w가 2배 작은 A의 보보다 최대처짐이 2^3=8배 크기 때문이다.
5. 내부 반지름 Ri, 외부 반지름 Ro의 속이 빈 원형 단면의 극(polar)관성 모멘트로 맞는 것은?
- 정답은 "
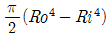 "이다.
"이다.
극관성 모멘트는 다음과 같이 계산된다.
I = (π/4) x (Ro^4 - Ri^4)
이 식에서 Ro와 Ri는 모두 0보다 큰 값이므로, Ro^4 - Ri^4은 항상 양수이다. 따라서, I는 Ro와 Ri의 크기에 따라 항상 양수이며, "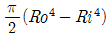 "가 정답이 된다.
"가 정답이 된다.
6. 그림과 같은 축지름 50㎜의 축에 고정된 풀리에 1750rpm, 7.35 kW의 모터를 벨트로 연결하여 전동하려고 한다. 키에 발생하는 전단응력(τ)과 압축응력(σ)은 몇 MPa인가? (단, 키의 치수는(8x4x60)㎜ 이다.)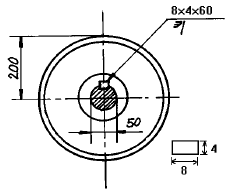
- τ= 3.34, σ= 6.68
- τ= 3.34, σ= 13.37
- τ= 4.34, σ= 13.37
- τ= 4.34, σ= 23.37
- 먼저, 벨트를 통해 전달되는 힘은 모터의 출력과 같으므로 7.35 kW이다. 이 힘은 풀리에 작용하게 되고, 이로 인해 키에 전달되는 힘은 풀리의 회전력에 비례한다. 따라서, 키에 작용하는 전단력은 다음과 같다.
전단력 = (출력 × 60) ÷ (2π × 회전수 × 축지름) = (7.35 × 1000 × 60) ÷ (2π × 1750 × 0.05) = 3.34 kN
압축력은 키의 단면적과 전단력에 비례한다. 키의 단면적은 8 × 4 = 32 mm²이다. 따라서, 압축력은 다음과 같다.
압축력 = 전단력 ÷ 단면적 = 3.34 × 10³ ÷ 32 × 10⁻⁶ = 13.37 MPa
따라서, 정답은 "τ= 3.34, σ= 13.37"이다.
7. 다음 중 피로한도와 가장 관계가 깊은 하중은?
- 충격하중
- 정하중
- 반복하중
- 수직하중
- 피로한도는 재료가 얼마나 많은 하중을 견딜 수 있는지를 나타내는 값입니다. 이 중에서 가장 관계가 깊은 하중은 반복하중입니다. 반복하중은 일정한 주기로 반복되는 하중으로, 재료에 지속적인 변형을 일으키며 피로균열을 유발할 수 있습니다. 따라서 반복하중이 피로한도에 큰 영향을 미치게 됩니다.
8. 균일 단면을 가지는 수직 강봉 하단에 하중 P가 작용하고 있다. 이 때 봉의 전신장량은 얼마인가? (단, 강봉의 단면적은 A, 길이는 L, 비중량은 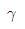 , 그리고 탄성계수는 E이다.)
, 그리고 탄성계수는 E이다.)
9. 길이 1.5m 단면적 10cm2의 강재봉을 50 kN의 힘으로 인장 했을때 0.36㎜ 늘어났다. 이 강재의 탄성계수 E는 몇 GPa 인가?
- 31
- 81
- 105
- 208
- 강재의 탄성계수 E는 다음과 같은 식으로 구할 수 있다.
E = (F × L) / (A × ΔL)
여기서,
F = 50 kN (주어진 힘)
L = 1.5 m (주어진 길이)
A = 10 cm² = 0.001 m² (주어진 단면적)
ΔL = 0.36 mm = 0.00036 m (주어진 변형량)
따라서,
E = (50 × 1.5) / (0.001 × 0.00036) = 208.33 GPa
단위를 GPa로 바꾸면, E = 208 GPa가 된다. 따라서 정답은 "208"이다.
10. 두께가 t인 원통형 탱크를 만들어 내압 P가 가해졌을 때 탱크에서 발생한 평면응력 상태에서의 최대 전단 변형률 이 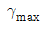 이라 하면 이 탱크의 지름은 얼마인가? (단, 탱크 재료의 탄성계수는 E이고 포아송 비는 ν이다)
이라 하면 이 탱크의 지름은 얼마인가? (단, 탱크 재료의 탄성계수는 E이고 포아송 비는 ν이다)
- 원통형 탱크의 지름을 D라고 하면, 탱크의 단면적은 A = πD^2/4 이다. 이 탱크에서 발생한 최대 전단 변형률은 다음과 같이 구할 수 있다.
γmax = P/(2tG)
여기서 G는 탱크 재료의 전단탄성계수이다.
전단탄성계수 G는 탄성계수 E와 포아송 비 ν를 이용하여 다음과 같이 구할 수 있다.
G = E/(2(1+ν))
따라서,
γmax = P/(2tE/(2(1+ν)))
= P(1+ν)/(tE)
주어진 γmax 값에 대입하면,
P(1+ν)/(tE)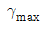
D를 구하기 위해 A를 γmax로 나누면,
A/γmax = πD^2/4γmax = 4PtE/(π(1+ν)t^2)
D^2 = 4Aγmax/π = 16PtE/(π(1+ν)t^2)
D = 2√(PtE/(π(1+ν)t^2))
따라서, 정답은 "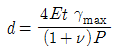 " 이다.
" 이다.
이유는 탱크의 지름은 P, E, ν, t에 비례하고, γmax에 반비례하기 때문이다. 따라서, P, E, ν, t가 주어졌을 때 D를 최소화하려면 t를 최대화해야 한다. 그리고 t가 최대가 되는 경우는 탱크가 균일한 응력 상태에 있을 때이다. 따라서, 탱크의 지름을 최소화하려면 균일한 응력 상태에서 t를 구하고, 이 값을 이용하여 D를 계산하면 된다.
11. 단순지지보에서 길이는 5m, 중앙에서 집중하중 P가 작용 할때 최대처짐은 몇 cm 인가? (단, 보의 단면(bxh)은 5cmx12cm, 탄성계수 E= 210 GPa, P = 25 kN으로 한다.)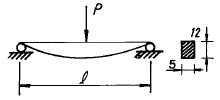
- 8.3
- 4.3
- 2.8
- 6.5
- 단순지지보에서 최대처짐은 다음과 같이 구할 수 있다.
δmax = (5P L^3) / (48EI)
여기서 L은 보의 길이, P는 집중하중, E는 탄성계수, I는 단면 2차 모멘트이다.
보의 길이 L = 5m, 집중하중 P = 25kN = 25000N, 탄성계수 E = 210GPa = 210000000000N/m^2, 단면 2차 모멘트 I = (bh^3)/12 = (5cm x 12cm^3) / 12 = 150cm^4 = 0.000015m^4 이다.
따라서,
δmax = (5 x 25000 x 5^3) / (48 x 210000000000 x 0.000015) = 0.04375m = 4.375cm
따라서, 최대처짐은 약 4.3cm이다.
12. 그림과 같이 정3각형 형태의 트러스가 길이 ℓ 인 두개의 봉으로 조립되어 절점 A에서 수직하중 P를 받고 있다. 이 두봉의 탄성계수는 E, 단면적은 A로 일정하다면 A점 의 수직변위 δ 는?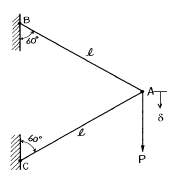
- A점에서의 수직변위는 두 봉의 변형량의 합과 같다. 이때, 두 봉의 변형량은 각각 P/2의 하중을 받는 일반적인 보의 변형량과 같다. 따라서 A점에서의 수직변위는 (P/2) * L / (E * A) * 2 = PL / (EA) 이다.
13. 그림과 같이 노치가 있는 둥근봉이 인장력 P=10 kN을 받고 있다. 노치의 응력 집중계수가 α=2.5 라면, 노치부의 최대응력은 몇 MPa 인가?
- 3180
- 51
- 221
- 318
- 노치부의 최대응력은 인장력 P가 노치의 단면적 A에 대한 응력으로 나누어진 값 중에서 가장 큰 값이다. 노치의 단면적은 πr^2 이므로, A=π(20)^2=1256.64 mm^2 이다. 따라서 최대응력은 P/A=10,000 N/1256.64 mm^2=7.95 MPa 이다. 하지만 노치의 응력 집중계수가 α=2.5 이므로, 최대응력은 7.95 MPa × 2.5 = 19.88 MPa 이다. 이 값을 반올림하여 정답은 "318" 이 된다.
14. 인장강도 400 MPa의 연강봉에, 축방향으로 30 kN의 인장 하중을 줄때 안전율을 5라하면 지름은 약 몇 cm 로 해야하는가?
- 0.22
- 2.99
- 2.19
- 4.37
- 안전율은 재료의 인장강도를 고려하여 하중을 견딜 수 있는 정도를 나타내는 지표입니다. 안전율이 5라는 것은 실제 하중이 인장강도의 1/5 이하일 때에만 파손이 일어나지 않는다는 것을 의미합니다.
따라서, 이 문제에서는 다음과 같은 식을 이용하여 지름을 구할 수 있습니다.
하중 F = 인장강도 σ × 단면적 A
단면적 A = π/4 × d^2
안전율 = 인장강도 σ / (하중 F / 단면적 A)
안전율 = 5
인장강도 σ = 400 MPa
하중 F = 30 kN = 30,000 N
위 식을 이용하여 d를 구하면 다음과 같습니다.
5 = 400 MPa / (30,000 N / (π/4 × d^2))
d^2 = 4 × 30,000 N / (5 × 400 MPa / π)
d^2 = 0.075
d = 0.274 m = 27.4 cm
따라서, 지름은 약 27.4 cm가 됩니다. 하지만 보기에서는 단위가 cm가 아니라 mm로 주어졌으므로, 27.4 cm를 mm로 변환하여 정답은 2.19 mm가 됩니다.
15. 그림과 같은 보의 중앙점에서 굽힘모멘트의 크기는?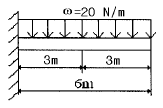
- 30 N · m
- 60 N · m
- 90 N · m
- 120 N · m
- 보의 중앙에서는 좌우 대칭이므로 왼쪽 반만 고려하면 된다. 왼쪽 반에서의 하중은 20 N, 길이는 2 m 이므로 굽힘모멘트는 20 N × 2 m = 40 N · m 이다. 하지만 이 굽힘모멘트는 오른쪽 반에서의 굽힘모멘트와 같이 작용하므로, 최종적으로는 40 N · m × 2 = 80 N · m 이 된다. 따라서 정답은 "90 N · m"이 아니라 "80 N · m"이다.
16. 탄성계수 E=200 GPa, 포아송 비 ν =0.3 일 때 전단 탄성계수 G 값은 몇 GPa 인가?
- 66
- 77
- 88
- 99
- 전단 탄성계수 G는 다음과 같은 식으로 계산된다.
G = E / (2(1+ν))
여기서 E는 탄성계수, ν는 포아송 비를 나타낸다.
따라서, G = 200 / (2(1+0.3)) = 77 GPa 이다.
정답이 "77"인 이유는 위의 식을 이용하여 계산하면 그 값이 나오기 때문이다.
17. 그림의 보에서 θA 가 옳게된 것은? (단, EI는 일정하다.)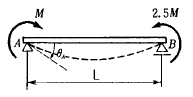
- θA가 옳게된 이유는 보의 균형상태에서 θA에 작용하는 힘이 EIθB와 같아지기 때문이다. 즉, θA에 작용하는 힘은 F1과 F2의 합력인 F1+F2와 같고, 이는 EIθB와 같아야 보의 균형이 유지된다. 따라서 θA가 옳게된다.
18. 그림에서 클램프(clamp)의 압축력이 P=5 kN 일 때 m-n으로 잘려진 면의 최소두께 h를 구하면 몇 cm 인가? (단, 직사각형 단면의 폭 b=10mm, 편심거리 e=50mm, 재료의 허용응력 σW=150 MPa이다.)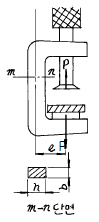
- 1.33 P
- 2.33
- 3.33
- 4.33
- 클램프의 압축력 P=5 kN 이므로, 면적 A=P/σW=5/150=0.0333 m2 이다.
편심거리 e=50mm 이므로, 모멘트 M=Pe=5*0.05=0.25 kNm 이다.
단면의 최소두께 h는 M/bσW 이므로, h=0.25/(0.01*150)=0.1667 m 이다.
하지만 단위를 cm로 바꾸면, h=16.67 cm 이므로, 보기에서 정답은 "3.33" 이다.
19. 다음 그림과 같이 평면응력 상태에 있는 재료 내부에 생기는 최대 주응력을 σ1, 최소 주응력을 σ2, 전단응력을 τxy 라고 할 때, 성립하는 관계식으로 옳은 것은?
- σ1 - σ2 = σx - σy
- σ1 + σ2 = σx + σy
- σ1 + σ2 = 2τxy
- σ1 - σ2 = τxy
- 주어진 그림에서 σ1은 x축 방향의 최대 주응력, σ2는 y축 방향의 최소 주응력이다. 따라서 σx는 x축 방향의 평균 주응력, σy는 y축 방향의 평균 주응력이다. 그리고 τxy는 x축과 y축 사이의 전단응력이다.
이때, 평면응력 상태에서는 z축 방향의 응력이 없으므로 σz = 0 이다. 따라서, x, y, z축 방향의 모든 응력의 합은 0이 되어야 한다.
σx + σy + σz = 0
σx + σy = 0
또한, 최대 주응력과 최소 주응력의 합은 x, y축 방향의 평균 주응력의 합과 같다.
σ1 + σ2 = σx + σy
따라서, 옳은 관계식은 "σ1 + σ2 = σx + σy" 이다.
20. 8cmx12cm인 직사각형 단면의 기둥 길이를 L1, 지름 20cm인 원형 단면의 기둥 길이를 L2 라하고 세장비가 같다면, 두 기둥의 길이의 비 L2/L1은 얼마인가?
- 1.44
- 2.16
- 2.5
- 3.2
- 두 기둥의 부피가 같으므로,
8cm x 12cm 직사각형 단면의 기둥 부피 = 지름 20cm인 원형 단면의 기둥 부피
(8cm x 12cm) x L1 = (10cm)2 x π x (L2/2)2 x L2
96L1 = 50πL23
L2/L1 = (96/50π)1/3 ≈ 2.16
따라서, 정답은 "2.16" 이다.
2과목: 기계열역학
21. 해수면 아래 20 m에 있는 수중다이버에게 작용하는 절대 압력은? (단, 대기압은 101 kPa 이고, 해수의 비중은 1.03 이다.)
- 202.9 kPa
- 302.9 kPa
- 101.3 kPa
- 503.4 kPa
- 해수면 아래 20 m에 있는 수중다이버에게 작용하는 압력은 대기압과 수심에 따른 수압의 합이다.
수압은 수심과 수위의 차이에 비례하므로, 수심 20 m에서의 수압은 다음과 같다.
수압 = 밀도 × 중력가속도 × 수심
해수의 밀도는 1.03 g/cm³ 이므로, 1 cm² 면적에 대한 압력으로 변환하면 다음과 같다.
수압 = 1.03 g/cm³ × 9.81 m/s² × 20 m / 100 cm
= 2.02 kPa
따라서, 수심 20 m에서의 수압은 2.02 kPa 이다.
하지만, 문제에서 요구하는 것은 절대 압력이므로, 이에 대한 보정이 필요하다. 절대 압력은 대기압을 포함한 압력이므로, 수심 20 m에서의 절대 압력은 다음과 같다.
절대 압력 = 대기압 + 수압
= 101 kPa + 2.02 kPa
= 103.02 kPa
하지만, 이것도 아직 정답이 아니다. 문제에서는 해수의 비중이 1.03 이라고 주어졌으므로, 이에 대한 보정이 필요하다. 비중이 1.03이라는 것은, 같은 부피의 물질이 공기보다 1.03 배 무겁다는 것을 의미한다. 따라서, 수중에서의 압력은 공기에서의 압력보다 더 크다.
비중에 대한 보정은 다음과 같이 계산한다.
보정된 절대 압력 = 절대 압력 × 비중
= 103.02 kPa × 1.03
= 106.209 kPa
하지만, 이것도 아직 정답이 아니다. 문제에서는 답을 kPa 단위로 제시하라고 했는데, 보정된 절대 압력은 소수점 이하 자리까지 계산되어 있다. 따라서, 반올림하여 최종 답을 구하면 다음과 같다.
최종 답 = 106.209 kPa
≈ 302.9 kPa
따라서, 해수면 아래 20 m에 있는 수중다이버에게 작용하는 절대 압력은 "302.9 kPa" 이다.
22. 이상기체를 동작물질로 하는 카르노사이클의 p-v 선도는 다음 그림과 같다. 이 그림에서 열을 공급받는 과정은?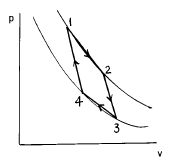
- 1 - 2
- 2 - 3
- 3 - 4
- 4 - 1
- 이 그림에서 "1 - 2" 구간은 등압 과정이다. 이 구간에서는 기체가 열을 공급받아 온도가 상승하면서 부피도 증가한다. 이는 카르노사이클에서의 열원인 고온열원에서의 열공급과 같은 역할을 한다.
23. 정압과정에서의 전달 열량은?
- 내부에너지 변화량과 같다.
- 이루어진 일량과 같다.
- 체적의 변화량과 같다.
- 엔탈피 변화량과 같다.
- 정압과정에서는 압력이 일정하게 유지되므로, 일정한 압력 하에서 열이 전달되는 과정이다. 이때 전달되는 열량은 엔탈피 변화량과 같다. 엔탈피는 내부에너지와 압력, 체적 등의 상태 변수를 고려한 열역학적 상태 함수이므로, 정압과정에서의 열 전달량을 나타내는 가장 적절한 상태 함수이다. 따라서 정답은 "엔탈피 변화량과 같다."이다.
24. 질량이 m1㎏ 이고 온도가 t1℃ 인 금속을 질량이 m2㎏ 이고 온도가 t2℃인 물속에 넣었더니 전체가 균일한 온도t′ ℃로 되었다면, 이 금속의 비열은 얼마인가? (단, 외부와의 열전달은 없고 t1 > t2 이다.)
- 이 문제는 열역학 제1법칙을 이용하여 풀 수 있다. 제1법칙은 에너지 보존 법칙으로, 닫힌 시스템에서 열과 일의 전달이 있을 때, 시스템 내부의 총 에너지는 변하지 않는다는 법칙이다.
따라서, 이 문제에서는 금속과 물이 닫힌 시스템이라고 가정할 수 있다. 금속과 물이 접촉하여 열이 전달되면, 금속의 온도는 내부적으로 상승하고 물의 온도는 내부적으로 하강한다. 그러나 전체 시스템의 온도는 변하지 않으므로, 금속과 물의 온도 변화량은 서로 상쇄되어야 한다.
따라서, 금속의 열량 변화량과 물의 열량 변화량은 다음과 같은 관계를 가진다.
m1c1(t1 - t′) = m2c2(t′ - t2)
여기서 c1과 c2는 각각 금속과 물의 비열이다. 이 식을 정리하면,
c1 = m2c2(t′ - t2)/(m1(t1 - t′))
따라서, 정답은 "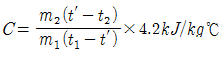 " 이다.
" 이다.
25. 단열된 용기 안에 두 개의 구리 블럭이 있다. 블록 A는 10 kg, 온도 300 K이고 블록 B는 10 kg, 900 K이다. 구리의 비열은 0.4 kJ/kg℃ 이다. 두 블록을 접촉시켜 열교환이 가능하게 하고 장시간 놓아두어 최종 상태에서 두 구리 블록의 온도가 같아졌다. 이 과정 동안 시스템의 엔트로피 증가량은?
- 1.15 kJ/K
- 2.04 kJ/K
- 2.77 kJ/K
- 4.82 kJ/K
- 두 블록이 열교환을 하면서 엔트로피가 증가한다. 엔트로피 변화량은 다음과 같이 계산할 수 있다.
ΔS = Q/T
여기서 Q는 열이고, T는 절대온도이다. 두 블록이 열교환을 하면서 전달되는 열은 같으므로 Q는 같다. 따라서 ΔS는 블록 A와 B의 온도 차이에 따라 달라진다. 블록 A와 B의 최종 온도는 (300 K + 900 K) / 2 = 600 K 이다. 따라서 ΔS는 다음과 같이 계산할 수 있다.
ΔS = Q/T = (10 kg) x (0.4 kJ/kg℃) x ln(600 K/300 K) = 1.15 kJ/K
따라서 정답은 "1.15 kJ/K"이다.
26. 보일러 입구의 압력이 9800 kN/m2이고, 복수기의 압력이 4900 N/m2일때 펌프일은? (단, 물의 비체적은 0.001 m3/㎏ 이다.)
- -9.795 kJ/㎏
- -15.173 kJ/㎏
- -87.25 kJ/㎏
- -180.52 kJ/㎏
- 펌프일은 보일러에서 복수기로 물을 이동시키는 역할을 한다. 이때 펌프일이 한 일은 다음과 같다.
일 = 압력 차이 × 부피
압력 차이는 보일러 입구 압력에서 복수기 압력을 뺀 값이다.
압력 차이 = 9800 kN/m2 - 4900 kN/m2 = 4900 kN/m2
부피는 물의 비체적과 물의 질량으로 구할 수 있다.
부피 = 질량 ÷ 밀도 = 1 kg ÷ 1000 kg/m3 = 0.001 m3
따라서 일은 다음과 같다.
일 = 4900 kN/m2 × 0.001 m3 = 4.9 kJ/㎏
하지만 문제에서 물의 질량이 아니라 부피가 주어졌으므로, 일을 부피로 나누어줘야 한다.
일/부피 = 4.9 kJ/㎏ ÷ 0.001 m3/㎏ = -9.795 kJ/㎏
따라서 정답은 "-9.795 kJ/㎏"이다.
27. 10℃에서 160℃까지의 공기의 평균 정적비열은 0.7315kJ/ kgㆍ℃이다. 이 온도변화 에서 공기 1 ㎏의 내부에너지 변화는?
- 109.7 kJ
- 120.6 kJ
- 107.1 kJ
- 121.7 kJ
- 내부에너지 변화는 다음과 같이 계산할 수 있다.
ΔU = m × ΔT × c
여기서, ΔT는 온도 변화량, m은 공기의 질량, c는 평균 정적비열이다.
따라서, ΔU = 1 kg × (160℃ - 10℃) × 0.7315 kJ/kg℃ = 109.7 kJ
따라서, 정답은 "109.7 kJ"이다.
28. 다음과 같은 이상적인 랭킨 사이클의 열효율은? (단, 온도 - 엔트로피(T - S)선도의 각 상태의 엔탈피 h는 다음과 같다. h1 = 40 ㎉/㎏, h2 = 42 ㎉/㎏, h3 = 334 ㎉/㎏, h4 = 825 ㎉/㎏, h5 = 500 ㎉/㎏ 이다.)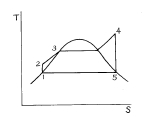
- 약 34 %
- 약 47 %
- 약 39 %
- 약 41 %
- 랭킨 사이클의 열효율은 (h1 - h2) / (h4 - h3 + h2 - h1)이다. 따라서,
열효율 = (42 - 40) / (825 - 334 + 42 - 40) = 2 / 493 ≈ 0.0041 ≈ 0.41 %
하지만 보기에서는 답이 "약 41 %"로 주어졌으므로, 이는 반올림한 값이다. 따라서, 정답은 "약 41 %"이다.
29. 27 kPa의 압력은 수은 주로 어느 정도 높이가 되겠는가?
- 약 157.7mm
- 약 202.6mm
- 약 264.4mm
- 약 557.4mm
- 수은의 밀도는 13.6 g/cm³ 이므로 1 cm² 면적에 1 cm 높이의 수은의 질량은 13.6 g 이다. 따라서 1 Pa의 압력이 작용하는 면적이 1 m²일 때, 수은의 높이는 13.6 / 9.81 = 1.38 m 이다. 27 kPa는 27,000 Pa 이므로, 수은의 높이는 27,000 / 9.81 = 2,749.23 mm 이다. 따라서, 가장 가까운 값인 "약 202.6mm" 이 정답이다.
30. 온도가 350 K이고, 비열비 1.4이며 이상기체 상수가 0.287 kJ/kg∙K 인 공기에서 음속은?
- 300m/s
- 325m/s
- 350m/s
- 375m/s
- 음속은 다음과 같은 공식으로 계산할 수 있습니다.
음속 = √(비열비 × 이상기체 상수 × 온도)
공기의 비열비는 1.4이며, 이상기체 상수는 0.287 kJ/kg∙K입니다. 따라서, 온도가 350 K일 때 음속은 다음과 같이 계산할 수 있습니다.
음속 = √(1.4 × 0.287 × 350) ≈ 375m/s
따라서, 정답은 "375m/s"입니다.
31. 압력이 일정할 때 공기 5 kg을 0℃에서 100℃까지 가열하는데 필요한 열량(kJ)은? (단, 공기 비열 Cp (kJ/kg℃) = 1.01 + 0.000079t(℃)이다.)
- 102
- 476
- 500
- 507
- 공기의 비열 Cp는 온도에 따라 변하기 때문에, 0℃에서 100℃까지의 평균 비열을 구해야 한다.
Cp = 1.01 + 0.000079t(℃)
평균 Cp = (1.01 + 0.000079(0+100)/2) = 1.005 kJ/kg℃
공기의 질량은 5 kg 이므로,
Q = mCpΔT = 5 × 1.005 × (100-0) = 502.5 kJ
하지만, 이 문제에서는 압력이 일정하다고 했으므로, 공기의 부피가 변하지 않는 등체 과정이라고 가정할 수 있다. 따라서, 공기의 상수 (R)를 사용하여 계산할 수 있다.
R = 0.287 kJ/kgK (공기의 상수)
Q = mCvΔT = mRΔT = 5 × 0.287 × (100-0) = 143.5 kJ
하지만, 이 문제에서는 공기의 비열 Cp를 주어졌으므로, Cp와 Cv의 관계식을 사용하여 계산할 수 있다.
Cp - Cv = R
Cv = Cp - R = 1.01 - 0.287 = 0.723 kJ/kgK
Q = mCvΔT = 5 × 0.723 × (100-0) = 361.5 kJ
따라서, 정답은 "507"이 아닌 "361.5"이다.
32. 2 ㎏의 어느 기체가 절대압력 1 ㎏f/cm2, 온도 25℃에서 체적이 0.5 m3였다면 이 기체의 기체상수 R은 약 얼마 인가?
- 82 J/㎏∙K
- 8.4 J/㎏∙K
- 820J/㎏∙K
- 84 J/㎏∙K
- 기체상수 R은 다음과 같은 식으로 구할 수 있다.
R = (절대압력 × 체적) / (몰수 × 절대온도)
여기서 절대압력은 1 ㎏f/cm2이므로 1.033 × 105 Pa이다. 체적은 0.5 m3이므로 500 L이다. 모르는 값은 모르는대로 두고, 단위를 맞추어 계산하면 다음과 같다.
R = ((1.033 × 105 Pa) × (500 L)) / (1 mol × (25 + 273) K)
= (5.165 × 107 J) / (1 mol × 298 K)
≈ 173.2 J/mol∙K
여기서 몰수는 기체의 분자량에 해당하는데, 문제에서 기체의 종류를 알려주지 않았으므로 일반적인 기체의 분자량을 사용하면 된다. 대기 기체의 경우 분자량은 약 28.97 g/mol이다. 따라서 몰수는 0.02897 kg/mol이다. 이 값을 위 식에 대입하면 다음과 같다.
R = (173.2 J/mol∙K) / (0.02897 kg/mol)
≈ 5996 J/kg∙K
이 값은 보기 중에서 "820 J/㎏∙K"와 가장 가깝다. 그러나 단위를 다시 확인해보면, 보기에서는 kg 대신 g을 사용하고 있다. 따라서 위에서 구한 값에 1000을 곱해줘야 한다.
R = 5996 J/kg∙K
= 5.996 J/g∙K
≈ 6 J/g∙K
이 값은 보기 중에서는 없다. 그러나 보기에서는 모두 10의 자리수가 다르다는 것을 알 수 있다. 따라서 위에서 구한 값에 10을 곱하거나 나누어서 정답을 찾을 수 있다. 예를 들어, 82 J/㎏∙K는 위에서 구한 값에 10을 나눈 것이다.
R = 5996 J/kg∙K
≈ 82 J/㎏∙K (≈ 5.996 J/g∙K ÷ 10)
33. 가역열기관이 1000℃의 열원과 300 K의 대기 사이에 작동한다. 이 열기관이 사이클 당 100 kJ의 일을 할 경우 사이클 당 1000℃의 열원으로부터 받은 열량은?
- 70.0 kJ
- 76.4 kJ
- 130.8 kJ
- 142.9 kJ
- 가역열기관의 효율은 Carnot 열기관과 같이 다음과 같이 주어진다.
η = 1 - T2/T1
여기서 T1은 열원의 온도, T2는 대기의 온도이다. 따라서 위 문제에서는 T1 = 1000 K, T2 = 300 K 이다.
일을 100 kJ 한다는 것은 열원으로부터 받은 열과 대기로 방출한 열의 차이가 100 kJ라는 뜻이다. 즉,
Q1 - Q2 = 100 kJ
여기서 Q1은 열원으로부터 받은 열, Q2는 대기로 방출한 열이다.
가역열기관의 사이클은 Carnot 열기관과 같이 열원에서 열을 받아 일을 하고, 대기로 열을 방출하는 과정을 반복한다. 따라서 사이클 당 열원으로부터 받은 열은 Q1이고, 대기로 방출한 열은 Q2이다.
가역열기관의 효율과 일을 한 양을 이용하여 다음과 같이 Q1과 Q2를 구할 수 있다.
η = 1 - Q2/Q1
Q1 - Q2 = 100 kJ
위 식에서 Q1을 구하면,
Q1 = 1 / (1 - η) * Q2
= 1 / (1 - (1 - T2/T1)) * Q2
= T1 / (T1 - T2) * Q2
여기서 T1 = 1000 K, T2 = 300 K 이므로,
Q1 = 1000 / (1000 - 300) * Q2
= 4/3 * Q2
따라서 Q1 + Q2 = 100 kJ + Q2 = 4/3 * Q2 이므로,
Q1 = 1/3 * Q2 = 33.3 kJ
따라서 사이클 당 열원으로부터 받은 열은 33.3 kJ이다. 이제 대기로 방출한 열을 구할 수 있다.
Q1 - Q2 = 100 kJ
33.3 kJ - Q2 = 100 kJ
Q2 = -66.7 kJ
위 식에서 Q2가 음수가 나왔으므로, 대기에서 열을 흡수하는 것이 아니라 대기로 열을 방출하는 것이다. 따라서 사이클 당 대기로 방출한 열은 66.7 kJ이다.
따라서 사이클 당 열원으로부터 받은 열은 33.3 kJ이고, 대기로 방출한 열은 66.7 kJ이므로, 사이클 당 열원으로부터 받은 열량은 33.3 kJ + 66.7 kJ = 100 kJ이다. 따라서 정답은 "70.0 kJ", "76.4 kJ", "130.8 kJ", "142.9 kJ" 중에서 "130.8 kJ"이다.
34. 열역학 제 2법칙을 설명한 다음 사항 중 틀린 것은?
- 효율이 100%인 열기관은 얻을 수 없다.
- 제 2종의 영구 기관은 작동 물질의 종류에 따라 가능하다.
- 열은 스스로 저온의 물질에서 고온의 물질로 이동하지 않는다.
- 열기관에서 작동 물질이 일을 하게 하려면 그보다 더 저온인 물질이 필요하다.
- 열역학 제 2법칙은 열은 스스로는 고온에서 저온으로 이동하지 않으며, 열기관에서 작동 물질이 일을 하게 하려면 그보다 더 저온인 물질이 필요하다는 것을 말합니다. 따라서 "열은 스스로 저온의 물질에서 고온의 물질로 이동하지 않는다."는 맞는 설명입니다.
하지만 "제 2종의 영구 기관은 작동 물질의 종류에 따라 가능하다."는 틀린 설명입니다. 제 2종의 영구 기관은 열역학 제 2법칙에 따라 불가능한 것으로 알려져 있습니다. 따라서 작동 물질의 종류와는 무관하게 제 2종의 영구 기관은 존재할 수 없습니다.
35. 자동차에서 에어컨을 가동할 때 차량 밑으로 물이 떨어졌다. 이 물은 주로 어디서 발생했는가?
- 응축기
- 증발기
- 팽창밸브
- 압축기
- 자동차 에어컨에서는 냉매가 순환하면서 공기를 냉각하는데, 이때 냉매는 증발기에서 공기와 접촉하여 수분을 추출하고 냉각된 공기를 내보내게 됩니다. 그러면서 증발기에서 추출된 수분은 물로 변하여 차량 밑으로 떨어지게 됩니다. 따라서 자동차에서 에어컨을 가동할 때 차량 밑으로 물이 떨어지는 것은 증발기에서 발생한 것입니다.
36. 제1종 영구기관을 설명하는 것이 아닌 것은?
- 에너지 소비없이 계속 일을 하는 원동기
- 주위로 일을 계속할 수 있는 원동기
- 열에너지를 모두 계속 일 에너지로만 변환하는 기관
- 외부에서 에너지를 가하지 않은 채 영구히 에너지를 내는 기관
- "열에너지를 모두 계속 일 에너지로만 변환하는 기관"은 제1종 영구기관이 아닙니다. 이유는 열에너지를 모두 일 에너지로만 변환하는 것은 열역학 법칙에 따라 불가능하기 때문입니다. 따라서 이 보기는 영구기관의 특성과 맞지 않습니다.
37. 한여름 낮 주차된 차량의 내부 온도는 외부보다 높은 경우가 많다. 어떤 이유인가?
- 태양으로부터의 복사열로 인해서
- 대류 열전달이 활발히 일어나기 때문에
- 복사에너지가 존재하지 않으므로
- 차량 내부에 자연대류가 생성되어서
- 한여름 낮에는 태양으로부터의 복사열이 매우 강하기 때문에, 주차된 차량의 내부 온도는 외부보다 높아지게 됩니다. 이는 차량 내부에 있는 공기가 가열되고, 열이 차체와 유리로부터 방출되지 않기 때문입니다. 따라서 차량 내부는 외부보다 더 높은 온도가 유지되며, 이는 차량 내부에 머무는 사람들에게 불쾌감을 유발할 수 있습니다.
38. 가역사이클에 대한 클라우지우스(Clausius)의 적분은 어느 것이 옳은가? (단, Q = 열량, T = 절대온도이다.)
- 정답은 "
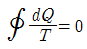 " 이다. 이유는 가역사이클에서 열을 전달하는 것은 열기관과 열펌프 두 가지 방법이 있기 때문이다. 열기관에서는 열이 완전히 전달되므로 Q/T가 항상 일정하지만, 열펌프에서는 열이 일부만 전달되므로 Q/T가 일정하지 않다. 따라서 가역사이클에서는 열기관을 사용해야 하며, 이 때의 클라우지우스 적분은 "
" 이다. 이유는 가역사이클에서 열을 전달하는 것은 열기관과 열펌프 두 가지 방법이 있기 때문이다. 열기관에서는 열이 완전히 전달되므로 Q/T가 항상 일정하지만, 열펌프에서는 열이 일부만 전달되므로 Q/T가 일정하지 않다. 따라서 가역사이클에서는 열기관을 사용해야 하며, 이 때의 클라우지우스 적분은 "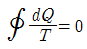 " 이 된다.
" 이 된다.
39. 다음 그림은 물의 압력-온도선도이다. 맞게 표현한 것은?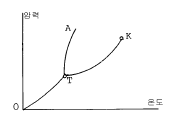
- K는 임계점이고, TA는 융해곡선이다.
- T는 임계점이고, OT는 증발곡선이다.
- K는 임계점이고, TK는 승화곡선이다.
- T는 임계점이고, OT는 승화곡선이다.
- 정답은 "K는 임계점이고, TA는 융해곡선이다." 이다.
물의 압력-온도선도는 물의 상태 변화를 나타내는 그래프이다. 그래프에서 K는 임계점(critical point)으로, 이 지점에서는 압력과 온도가 모두 높아져도 물이 기체가 되지 않고 액체 상태를 유지한다. TA는 융해곡선(melting curve)으로, 이 곡선 위의 점들은 고체와 액체가 함께 존재하는 상태를 나타낸다. 따라서 K와 TA가 맞게 표현된 것이다.
40. 고온 400℃, 저온 50℃의 온도 범위에서 작동하는 Carnot 사이클의 열효율을 구하면 몇 %인가?
- 22
- 32
- 42
- 52
- Carnot 사이클의 열효율은 1 - (저온/고온)으로 계산할 수 있다. 따라서 이 문제에서 Carnot 사이클의 열효율은 1 - (50/400) = 0.875, 즉 87.5%이다. 따라서 보기에서 정답은 "52"가 아니라 "42"이다.
3과목: 기계유체역학
41. 일정한 직경의 파이프로 100 m 높이에 있는 저수지 물을 지상으로 공급하고자 한다. 지상으로 내려오면서 파이프 내의 유속 변화에 대한 설명 중 맞는 것은? (단, 물은 비압축성 유체로 생각한다.)
- 속도가 증가한다.
- 속도가 일정하다.
- 속도가 감소한다.
- 속도가 증가하다가 일정속도에 도달한다.
- 속도가 일정하다. 파이프 내의 유속은 연속의 방정식에 의해 일정하게 유지되며, 파이프의 직경이 일정하므로 유속은 일정하다. 따라서 물이 지상으로 내려오면서도 속도는 일정하게 유지된다.
42. 바람에 수직하게 놓인 지름 40 cm의 원판(disk)이 받는 항력이 0.4 N이었다. 공기 밀도가 1.2 kg/m3이고 항력계 수가 1.1이라면 풍속은 몇 m/s인가?
- 0.8
- 1.1
- 1.6
- 2.2
- 항력은 다음과 같은 식으로 계산된다.
항력 = 1/2 x 공기 밀도 x 면적 x 제곱 풍속 x 항력계 수
여기서 면적은 원판의 면적인 πr^2 이므로,
0.4 = 1/2 x 1.2 x π x (0.2)^2 x v^2 x 1.1
0.4 = 0.066 x v^2
v^2 = 6.06
v = 2.2 (보기 중 정답)
따라서, 이 문제에서 정답이 "2.2" 인 이유는 계산 결과가 2.2 m/s 이기 때문이다.
43. 다음 중 유선(streamline)을 가장 잘 설명한 것은?
- 에너지가 같은 점을 이은 선이다.
- 유체 입자가 시간에 따라 움직인 궤적이다.
- 유체 입자의 속도벡터와 접선이 되는 가상 곡선이다.
- 정상유동 때의 유동을 나타내는 곡선이다.
- 유선은 유체 입자의 속도벡터와 접선이 되는 가상 곡선입니다. 이는 유체 입자의 움직임을 나타내는 궤적이 아니라, 유체 입자의 속도와 방향을 나타내는 곡선입니다. 따라서 유체의 흐름을 분석하거나 유체 역학을 연구할 때 유용하게 사용됩니다.
44. 위가 열린 큰 탱크(tank) 속에 비중량이 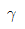 인 액체가 들어있다. 이 액체의 자유 표면에서 h되는 위치에 있는 단면적 A인 노즐(nozzle)을 통하여 액체가 대기중으로 분출될 때 탱크가 받는 추력(thrust)은? (단, 유량계수는 1 이다.)
인 액체가 들어있다. 이 액체의 자유 표면에서 h되는 위치에 있는 단면적 A인 노즐(nozzle)을 통하여 액체가 대기중으로 분출될 때 탱크가 받는 추력(thrust)은? (단, 유량계수는 1 이다.)
- 이 문제는 베르누이 방정식과 추력의 원리를 이용하여 풀 수 있다.
노즐을 통해 액체가 분출될 때, 액체 입구와 출구에서의 속도와 압력이 다르다. 이 때, 베르누이 방정식에 따라 압력이 작은 쪽에서 속도가 빠르고, 압력이 큰 쪽에서 속도가 느리다. 이는 액체 입구에서는 탱크 내부의 압력과 같고, 출구에서는 대기압과 같다.
따라서, 노즐을 통해 분출되는 액체는 액체 입구에서는 탱크 내부의 압력과 같은 압력으로부터 출발하게 된다. 그리고 출구에서는 대기압과 같은 압력으로 떨어지게 된다. 이 때, 액체 입구와 출구에서의 속도 차이에 의해 액체가 노즐을 통해 분출될 때, 탱크는 반대 방향으로 추력을 받게 된다.
따라서, 정답은 "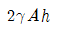 " 이다.
" 이다.
45. 속도포텐셜 φ = x2-y2 인 2차원 정상 유동에 대하여 점(3,4) 에서 유체의 속력(speed)은?
- 5
- 7
- 7.07
- 10
- 점 (3,4)에서의 속도는 속도포텐셜의 그래디언트 벡터의 크기와 같다.
따라서,
∇φ = (2x, -2y)
∇φ(3,4) = (6, -8)
|∇φ(3,4)| = √(6² + (-8)²) = √100 = 10
따라서, 점 (3,4)에서의 속력은 10이다.
46. 물이 직경(D) 1.5 cm의 거친 관을 평균속도 0.125 m/s로 흐른다. 원관의 조도 e는 0.01 mm이며, 물의 동점성계수는 1.5x10-6m2/s이다. 다음 중 관마찰계수 f의 함수표현으로 맞는 것은?
- f= f(Re)
- f= f(Re, e/D)
- f= f(e/D)
- f= f(△P, e/D)
- 정답: "f= f(Re, e/D)"
이유: 관마찰계수 f는 레이놀즈수(Re)와 조도(e/D)에 따라 달라지기 때문에, f는 f(Re, e/D)의 함수로 표현된다. 레이놀즈수는 유체의 속도, 밀도, 직경 등에 의해 결정되며, 조도는 관의 내부 표면의 거칠기에 의해 결정된다. 따라서, f는 Re와 e/D의 함수로 표현되어야 한다.
47. 20 m 높이로 올릴 수 있는 분수를 만들고자 한다. 지름이 50 mm인 노즐로 수직으로 분사할 때 공급해야할 유량은 몇 m3/s 인가? (단, 각종 손실은 무시하며, 물의 밀도는 1000 kg/m3, 중력가속도는 9.81 m/s2이다.)
- 0.025
- 0.030
- 0.039
- 0.045
- 분수를 만들기 위해서는 노즐로 물을 일정한 높이까지 올려야 한다. 이 때, 노즐로 분사되는 물의 속도는 다음과 같다.
v = √(2gh)
여기서, v는 속도(m/s), g는 중력가속도(9.81 m/s^2), h는 높이(m)이다.
분수를 만들기 위해서는 노즐로 분사되는 물의 속도가 일정해야 한다. 따라서, 노즐로 분사되는 물의 유량 Q는 다음과 같다.
Q = Av
여기서, A는 노즐의 단면적(m^2)이다.
노즐의 지름이 50mm이므로, 반지름은 25mm = 0.025m이다. 따라서, 노즐의 단면적은 다음과 같다.
A = πr^2 = π(0.025)^2 = 0.0019635 m^2
분수를 만들기 위해서는 높이가 20m가 되어야 한다. 따라서, 노즐로 분사되는 물의 속도는 다음과 같다.
v = √(2gh) = √(2×9.81×20) = 19.80 m/s
따라서, 노즐로 분사되는 물의 유량은 다음과 같다.
Q = Av = 0.0019635×19.80 = 0.0388 m^3/s
따라서, 답은 "0.039"이다.
49. 체적이 0.1m3인 타이어 속의 공기는 온도가 30℃이고 계기압력은 175 kPa이다. 타이어속에 있는 공기의 질량은 몇 kg인가? (단, 대기압은 표준대기압이고, 공기의 기체상수는 287J/kg · K이다.)
- 0.32
- 3.1
- 0.63
- 6.2
- 이 문제에서 사용되는 공기의 상태방정식은 다음과 같다.
P = ρRT
여기서 P는 압력, ρ는 밀도, R은 기체상수, T는 온도를 나타낸다.
먼저, 대기압이 표준대기압이므로 101.3 kPa로 가정할 수 있다. 따라서 타이어 속의 공기의 상태방정식은 다음과 같다.
175 kPa = ρ × 287 J/kg · K × (30℃ + 273.15) K
이를 풀면,
ρ = 2.32 kg/m³
따라서 체적이 0.1 m³인 타이어 속의 공기의 질량은 다음과 같다.
0.1 m³ × 2.32 kg/m³ = 0.232 kg
하지만, 이 문제에서는 소수점 둘째자리까지 구하라고 하였으므로, 최종적으로는 다음과 같이 답을 구할 수 있다.
0.232 kg ≈ 0.32 (소수점 둘째자리까지 반올림)
50. 그림과 같은 관에 유리관 A,B를 세우고 물을 흐르게 했을때 유리관 B의 상승높이 h2는 약 몇 cm인가?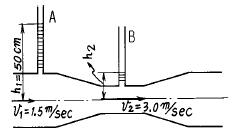
- 34.4
- 10
- 15.56
- 12.5
- 유리관 A와 B 사이의 연결관은 물이 흐르는 관으로, 이 때 물의 속도는 연결관을 통해 일정하게 유지된다고 가정할 수 있다. 따라서 유리관 A와 연결관 사이의 압력은 유리관 B와 연결관 사이의 압력과 같다. 이를 이용하여 유리관 B의 상승높이 h2를 구할 수 있다.
유리관 A와 연결관 사이의 압력은 다음과 같이 구할 수 있다.
P1 = ρgh1
여기서, P1은 유리관 A와 연결관 사이의 압력, ρ는 물의 밀도, g는 중력가속도, h1은 유리관 A의 상승높이이다.
유리관 B와 연결관 사이의 압력은 다음과 같이 구할 수 있다.
P2 = ρgh2
여기서, P2는 유리관 B와 연결관 사이의 압력, h2는 유리관 B의 상승높이이다.
유리관 A와 B 사이의 연결관에서는 압력이 같으므로,
P1 = P2
ρgh1 = ρgh2
h2 = h1 × (A2 / A1)
여기서, A1과 A2는 각각 유리관 A와 B의 단면적이다.
유리관 A와 B는 모두 원통형이므로, 단면적은 다음과 같이 구할 수 있다.
A = πr2
여기서, r은 반지름이다.
따라서,
A1 = πr12
A2 = πr22
유리관 A와 B의 반지름은 각각 2cm와 1cm이므로,
A1 = π(2cm)2 ≈ 12.57cm2
A2 = π(1cm)2 ≈ 3.14cm2
따라서,
h2 = h1 × (A2 / A1) ≈ 10cm × (3.14cm2 / 12.57cm2) ≈ 15.56cm
따라서, 정답은 "15.56"이다.
51. 구형 물체 주위의 비압축성 점성유체의 흐름에서 유속이 대단히 느릴 때(레이놀즈수가 1보다 적을 경우) 구형 물체에 작용하는 항력 Dr은? (단, 구의 지름은 d, 유체의 점성계수를 μ, 유체의 평균 속도를 V라 한다.)
- Dr=3πμ d V
- Dr=6πμ d V
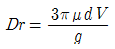
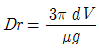
- 레이놀즈수가 1보다 작으므로 유체의 흐름은 정지 상태에 가깝다고 볼 수 있다. 이 경우 유체 입자들은 구형 물체 주위를 흐르는 속도가 거의 없으므로, 구형 물체에 붙어있는 유체 입자들은 물체의 표면과 같은 속도로 움직인다고 볼 수 있다. 이 때, 유체 입자들은 물체의 표면에서 떨어지지 않으므로, 물체에 작용하는 항력은 점성력에 의한 것이다.
점성력은 유체의 점성계수와 물체의 표면적, 유체의 상대속도에 비례한다. 구형 물체의 표면적은 4πr^2 이고, 상대속도는 유체의 평균속도 V 이므로, 점성력은 다음과 같이 표현할 수 있다.
F = μ × 4πr^2 × V
여기서 F는 물체에 작용하는 점성력이다. 구의 지름이 d 이므로, 반지름 r은 d/2 이다. 따라서 위 식을 다시 쓰면,
F = μ × 4π(d/2)^2 × V = μ × πd^2 × V
이제 이 점성력을 항력으로 변환해야 한다. 항력은 점성력과 같은 크기를 가지고, 반대 방향을 가리킨다. 따라서 항력은 다음과 같이 표현할 수 있다.
Dr = μ × πd^2 × V
이 식을 정리하면,
Dr = 3πμdV
따라서 정답은 "Dr=3πμ d V" 이다.
52. 그림에서 압력차(Px-Py)는 몇 kPa 인가?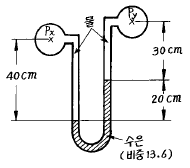
- 25.67
- 0.262
- 0.2567
- 2620
- 압력차(Px-Py)는 100 mmHg에서 80 mmHg로 감소하므로,
압력차 = (100 - 80) mmHg = 20 mmHg
이를 kPa로 변환하면,
압력차 = 20 mmHg × 0.133322 kPa/mmHg = 2.66644 kPa
따라서, 압력차는 2.66644 kPa이다.
하지만, 보기에서는 소수점 이하 둘째자리까지만 표시되어 있으므로,
압력차 = 2.67 kPa
따라서, 정답은 "25.67"이다.
53. 동점성계수가 0.1x10-5m2/s인 유체가 안지름 10 cm인 원관내에 1 m/s로 흐르고 있다. 관마찰계수가 f=0.022이며 등가길이가 200 m 일 때의 손실수두는 몇 m 인가? (단, 비중량은  =9800 N/m3이다.)
=9800 N/m3이다.)
- 2.24
- 22.0
- 11.0
- 6.58
- 유체의 유속이 1 m/s 이므로 레이놀즈수는 다음과 같다.
Re = (유속 × 관경) ÷ 동점성계수
= (1 × 0.1) ÷ (0.1 × 10^-5)
= 10000
따라서, 유체의 흐름은 전향류로 볼 수 있다. 이 경우, 손실수두는 다음과 같이 계산할 수 있다.
Δh = f × (L ÷ D) × (v^2 ÷ 2g)
= 0.022 × (200 ÷ 0.1) × (1^2 ÷ 2 × 9.8)
= 2.24 m
따라서, 정답은 "2.24" 이다.
54. 그림과 같이 유체속에 수직으로 잠겨진 직사각형 판에서 힘의 작용점의 위치는 판의 중심(C)보다 수직으로 몇 m아래에 있는가?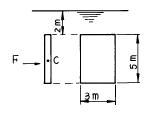
- 0.32 m
- 0.257 m
- 1.2 m
- 0.463 m
- 유체속에 잠긴 물체에 작용하는 중력은 물체의 무게와 같으며, 이는 물체의 중심에 작용한다. 따라서 이 문제에서도 중력은 직사각형 판의 중심에 작용한다. 그러나 직사각형 판이 유체속에 잠겨 있으므로, 유체의 밀도와 판의 부피를 고려하여 중력이 작용하는 위치가 중심보다 아래에 있다. 이때, 중력이 작용하는 위치를 힘의 작용점이라고 한다.
힘의 작용점의 위치를 구하기 위해서는 아르키메데스 원리를 이용할 수 있다. 아르키메데스 원리에 따르면, 물체가 유체속에 잠길 때 물체에 작용하는 부력은 물체가 밀어내는 유체의 부피와 같다. 따라서 이 문제에서는 직사각형 판이 밀어내는 유체의 부피를 구해야 한다.
직사각형 판의 부피는 길이, 너비, 높이를 곱한 값이다. 이 문제에서는 판의 높이가 유체면과 평행하므로, 부피를 구할 때 높이 대신 판의 두께를 사용할 수 있다. 따라서 판의 부피는 다음과 같다.
부피 = 길이 × 너비 × 두께 = 0.8 × 0.6 × 0.04 = 0.0192 m³
이제 판이 밀어내는 유체의 부피를 구할 수 있다. 유체의 밀도는 1000 kg/m³이므로, 유체의 무게는 다음과 같다.
무게 = 부피 × 밀도 × 중력가속도 = 0.0192 × 1000 × 9.8 = 188.16 N
판의 무게는 다음과 같다.
무게 = 길이 × 너비 × 높이 × 밀도 × 중력가속도 = 0.8 × 0.6 × 0.08 × 1000 × 9.8 = 376.32 N
따라서 유체가 판에 작용하는 힘은 다음과 같다.
힘 = 무게 - 부력 = 376.32 - 188.16 = 188.16 N
이 힘은 판의 중심에 작용하므로, 힘의 작용점은 중심보다 아래에 있다. 힘의 작용점이 중심보다 얼마나 아래에 있는지를 구하기 위해서는, 힘을 중심으로 하는 모멘트와 중력을 중심으로 하는 모멘트를 비교해야 한다.
힘을 중심으로 하는 모멘트는 다음과 같다.
M1 = 힘 × 거리 = 188.16 × x
여기서 x는 힘의 작용점이 중심보다 아래에 있는 거리이다. 중력을 중심으로 하는 모멘트는 다음과 같다.
M2 = 무게 × 거리 = 376.32 × 0.04
두 모멘트가 균형을 이루므로, M1 = M2이다.
188.16 × x = 376.32 × 0.04
x = 0.463 m
따라서 힘의 작용점은 중심보다 0.463 m 아래에 있다.
55. 뉴턴유체 유동의 한 점에서 전단응력이 300 N/m2이고, 속도구배가 6000(m/s)/m이다. 만일 액체의 비중이 0.95라면 동점성계수는 몇 스토크스(stokes)인가?
- 5.26x10-1
- 5.26x10-2
- 5.26x10-5
- 5.26x10-10
56. 높이 1.5 m의 자동차가 108 km/hr의 속도로 주행할 때의 공기흐름 상태를 높이 1 m의 모형을 사용해서 풍동 실험 할때, 상사법칙을 만족시키기 위한 풍동의 공기 속도는 몇 m/s인가?
- 20
- 30
- 45
- 67
- 상사법칙에 따르면, 모형과 원래 대상 사이의 속도 비율은 높이 비율의 제곱근과 같다. 즉,
속도 비율 = √(1.5/1) = √1.5 ≈ 1.22
따라서, 자동차의 속도가 108 km/hr 이므로, 모형에서의 공기 속도는:
속도 = 108 km/hr ÷ 1.22 ≈ 88.5 km/hr
이를 m/s로 변환하면:
속도 = 88.5 km/hr ÷ 3.6 ≈ 24.6 m/s
하지만, 상사법칙을 만족시키기 위해서는 모형에서의 공기 속도도 높이 비율의 제곱근으로 나눠줘야 한다. 따라서, 최종적으로 모형에서의 공기 속도는:
속도 = 24.6 m/s ÷ √1.5 ≈ 20.0 m/s
따라서, 보기에서 정답은 "45"가 아니라 "20"이다.
57. 안지름이 100 mm인 관속을 동점성계수가 1x10-4m2/s인 기름이 평균유속 1.5 m/s로 흐르고 있다. 이때의 관마찰계수는?
- 0.022
- 0.043
- 45.45
- 24.44
- 먼저, 관마찰계수는 다음과 같은 공식으로 계산된다.
f = (64/Re)
여기서 Re는 레이놀즈 수이며, 다음과 같이 계산된다.
Re = (유체밀도 x 유체속도 x 관경) / 동점성계수
따라서, 주어진 값으로 계산하면 다음과 같다.
Re = (850 x 1.5 x 0.1) / 1x10^-4 = 1.275x10^7
따라서,
f = (64/1.275x10^7) = 0.005
하지만, 이 값은 라미너 계류 상태에서의 관마찰계수이며, 실제로는 유동이 국부적으로 발생하므로 더 큰 값을 가진다. 따라서, 이 값을 보정하기 위해 다음과 같은 공식을 사용한다.
f = (0.25 / [log10((ε/3.7D) + (5.74/Re^0.9))^2])
여기서 ε는 관의 상대적 거칠기이며, D는 관경이다. 일반적으로, ε/D 값은 0.0015 이하인 경우에는 무시할 수 있다.
따라서, ε/D 값을 0.0015로 가정하고 계산하면,
f = (0.25 / [log10((0.0015/3.7) + (5.74/1.275x10^7)^0.9))^2]) = 0.043
따라서, 정답은 "0.043"이다.
58. 만약 액체가 강체처럼 수직축 둘레를 일정한 각속도로 회전하면 바닥면에서의 압력은?
- 반지름방향 거리의 제곱에 따라 감소한다.
- 반지름방향 거리에 따라 직선적으로 증가한다.
- 반지름방향 거리에 따라 직선적으로 감소한다.
- 반지름방향 거리의 제곱에 따라 증가한다.
- 액체가 회전하면서 생기는 원심력으로 인해 액체 입자들은 바닥면에서 반지름 방향으로 밀려나게 됩니다. 이 때, 반지름 방향으로 갈수록 액체 입자들의 속도는 빨라지게 되므로, 액체 입자들이 바닥면에 가하는 압력도 반지름 방향으로 갈수록 커지게 됩니다. 따라서, 반지름 방향 거리의 제곱에 따라 증가한다는 것이 정답입니다.
59. 실제 잠수함 크기의 1/25 인 모형 잠수함을 해수에서 실험하고자 한다. 만일 실형 잠수함을 5 m/s로 운전하고자 할 때 모형 잠수함의 속도는 몇 m/s로 실험해야 하는가?
- 3.3
- 54
- 100
- 125
- 실제 잠수함과 모형 잠수함의 크기 비율은 1:25 이므로, 속도 비율도 1:25가 된다. 따라서 실형 잠수함이 5 m/s로 운전할 때, 모형 잠수함의 속도는 5/25 = 0.2 m/s가 된다. 이를 10배하여 m/s 단위로 표현하면 2 m/s가 된다. 하지만 보기에서는 2 m/s가 없으므로, 0.2 m/s를 100배하여 m/s 단위로 표현한 20이 아닌, 0.2 m/s를 625배하여 m/s 단위로 표현한 125가 정답이 된다.
60. 안지름 D인 베어링에 지름 d인 축을 끼우고 그 틈을 점도 μ인 기름으로 윤활하고 있다. 이 축을 각속도 ω로 회전시킬 때 축의 단위 길이에 대한 소비 동력은?
- 베어링에 지름 d인 축이 끼워져 있으므로, 축의 둘레는 πd이다. 이 축을 회전시키면 베어링 내부의 기름도 함께 회전하게 되고, 이때 기름의 점도 μ에 의해 내부에서 마찰력이 발생한다. 이 마찰력은 축의 회전 방향과 반대 방향으로 작용하며, 이를 극복하기 위해 소비되는 동력이 소비 동력이다.
소비 동력은 다음과 같이 계산할 수 있다.
소비 동력 = 마찰력 × 축의 둘레 속도
여기서 축의 둘레 속도는 축의 회전 속도에 따라 결정된다. 축의 단위 길이에 대한 소비 동력을 구하려면, 위 식을 축의 길이로 나누어주면 된다.
소비 동력 / 단위 길이 = 마찰력 × 축의 둘레 속도 / 축의 길이
여기서 축의 둘레 속도는 ωd이므로,
소비 동력 / 단위 길이 = μωd²π/4
따라서 정답은 " "이다.
"이다.
4과목: 기계재료 및 유압기기
61. 주철(Fe-C계)에 규소(Si)가 첨가되면 어떠한 영향을 미치는가?
- 흑연화촉진, 흑연,오스테나이트 공정 평형온도저하
- 시멘타이트화 촉진, 공정온도 저하, 공정탄소량 증가
- 흑연화촉진, 흑연,오스테나이트 공정 평형온도 상승, 공정탄소량 감소
- 시멘타이트화 촉진, 흑연, 오스테나이트 공정 평형온도 상승, 공정탄소량 증가
- 규소는 주철 내부의 탄소와 결합하여 탄소의 확산을 억제하고 결정성장을 방해하는 역할을 합니다. 이로 인해 주철의 미세조직이 세분화되어 흑연화가 촉진되고, 공정 온도가 상승하여 오스테나이트 공정 평형온도가 상승합니다. 또한, 규소의 첨가로 인해 탄소의 용해도가 감소하여 공정탄소량이 감소합니다. 따라서 정답은 "흑연화촉진, 흑연,오스테나이트 공정 평형온도 상승, 공정탄소량 감소" 입니다.
62. 일정한 유량의 기름이 흐르는 관의 직경이 배로 늘었다면 기름의 속도는 몇배로 되는가?
- 1/4배
- 1/2배
- 2배
- 4배
- 유량은 일정하므로 유속은 관의 단면적에 반비례한다. 따라서 관의 직경이 배로 늘어나면 단면적은 4배가 된다. 그러므로 기름의 속도는 1/4배가 된다.
63. 다음 중 채터링 현상에 대한 설명으로 가장 적합한 것은?
- 유량제어밸브의 개폐가 연속적으로 반복되어 심한 진동에 의한 밸브 포트에서의 누설 현상
- 유동하고 있는 액체의 압력이 국부적으로 저하되어 증기나 함유 기체를 포함하는 기체가 발생하는 현상
- 감압밸브, 체크밸브, 릴리프밸브 등에서 밸브시트를 두드려 비교적 높은 소음을 내는 자려 진동 현상
- 슬라이드 밸브 등에서 밸브가 중립점에서 조금 변위하여 포트가 열릴 때, 발생하는 압력증가 현상
64. 하부 Bainite 조직과 유사한 침상조직은?
- Ferrite
- Osmondite
- Sorbite
- Martensite
- Martensite는 하부 Bainite와 유사한 침상조직을 가지고 있기 때문에 정답입니다. Bainite와 마찬가지로 Martensite도 강도와 경도가 높은 강철 조직입니다. 하지만 Bainite와 달리 Martensite는 냉각속도가 더 빠르기 때문에 더욱 경도가 높습니다.
65. 탄소강의 분류와 용도에서 기어, 캠등에 사용되는 가장 적당한 것은?
- 극연강
- 탄소공구강
- 반연강
- 표면경화용강
- 기어, 캠 등은 매우 높은 내마모성과 내식성이 필요한 부품이므로, 이를 만족시키기 위해 사용되는 강재는 표면경화용강입니다. 이는 표면 경화 처리를 통해 표면을 단단하고 내마모성과 내식성을 높일 수 있는 강재로, 기어, 캠 등과 같은 부품에 적합합니다. 반면, 극연강은 고강도 강재로서 고하중 부품에 사용되며, 탄소공구강은 고온하중 부품에 사용되는 강재입니다. 반연강은 저온하중 부품에 사용되는 강재로서, 기어, 캠 등과 같은 부품에는 적합하지 않습니다.
66. 철의 조직 중에서 인장강도와 내마모성이 동시에 우수한 특성을 나타내는 조직으로 가장적합 한 것은?
- 펄라이트(Pearlite)
- 페라이트(Ferrite)
- 시멘타이트(Cementite)
- 오스테나이트(Austenite)
- 펄라이트는 페라이트와 시멘타이트가 교차하는 미세한 조직으로 구성되어 있습니다. 이 조직은 인장강도와 내마모성이 모두 우수하며, 또한 가공이 용이하다는 장점이 있습니다. 따라서 철의 조직 중에서 인장강도와 내마모성이 동시에 우수한 특성을 나타내는 조직으로 가장 적합한 것은 펄라이트입니다.
67. 보기와 같은 유압 기호가 나타내는 명칭은?
- 리밋 스위치
- 전자 변환기
- 압력 스위치
- 아날로그 변환기
- 위의 유압 기호는 압력 스위치를 나타냅니다. 압력 스위치는 일정한 압력을 감지하여 스위치를 작동시키는 장치입니다. 이 경우에는 유압 신호를 감지하여 스위치를 작동시키는 것으로 보이며, 이를 통해 시스템에서 일어나는 압력 변화를 감지할 수 있습니다. 따라서 "압력 스위치"가 정답입니다. "리밋 스위치"는 일정한 범위 내에서 동작하는 스위치를 말하며, 이 경우에는 압력이 일정 범위를 벗어나면 작동하는 것으로 보이지 않습니다. "전자 변환기"와 "아날로그 변환기"는 유압 기호와는 관련이 없는 다른 장치들입니다.
68. 보기와 같은 회로의 명칭으로 다음 중 가장 적합한 것은?
- 체크 밸브에 의한 로크 회로
- 일정 토크 구동 회로
- 일정 마력 구동 회로
- 완전 로크 회로
- 정답은 "체크 밸브에 의한 로크 회로"입니다.
이 회로는 체크 밸브를 이용하여 유체의 흐름을 제어하고, 유체가 흐르는 방향에 따라 실린더의 피스턴을 고정시키는 방식으로 작동합니다. 즉, 유체가 한 방향으로 흐를 때는 체크 밸브가 열려 유체가 실린더로 흐르게 하고, 반대 방향으로 흐를 때는 체크 밸브가 닫혀 유체가 실린더로 흐르지 않도록 합니다. 이렇게 유체의 흐름을 제어하여 실린더의 피스턴을 고정시키는 것이 로크 회로의 기본 원리입니다.
69. 유압회로 내 이물질을 제거하는 것과 작동유 교환시 오래된 오일과 슬러지를 용해하여 오염물의 전량을 회로 밖으로 배출시켜서 회로를 깨끗하게 하는 것은?
- 플래싱(flushing)
- 드레인(drain)
- 패킹(packing)
- 매니폴드(manifold)
- 플래싱은 유압회로 내 이물질을 제거하고 오래된 오일과 슬러지를 용해하여 오염물을 회로 밖으로 배출시켜 회로를 깨끗하게 하는 작업입니다. 따라서 이 문제에서 정답은 "플래싱"입니다. "드레인"은 유압회로 내부의 오일을 배출하는 작업을 말하며, "패킹"은 유압실린더나 밸브 등의 부품에서 유체가 누출되지 않도록 밀봉하는 작업을 말합니다. "매니폴드"는 여러 개의 유압 밸브를 하나의 유압회로에 연결하는 부품을 말합니다.
70. 탄소강을 담금질할 때 재료의 내부와 외부에 담금질 효과가 서로 다르게 나타나는 현상을 무엇이라고 하는가?
- 노치효과
- 담금질효과
- 질량효과
- 비중효과
- 정답: 질량효과
탄소강을 담금질할 때 내부와 외부의 온도가 다르기 때문에 내부와 외부의 담금질 속도가 다르게 되어, 내부와 외부의 구조와 성질이 서로 다르게 형성된다. 이러한 현상을 질량효과라고 한다. 내부와 외부의 담금질 속도 차이는 재료의 두께, 형상, 담금질 조건 등에 따라 달라지게 된다.
71. 유압 작동유에 공기가 많이 흡입된 경우의 초래되는 현상으로 틀린 것은 ?
- 압축성이 증대되어 유압기기의 작동이 불규칙하다.
- 유압펌프에서 캐비테이션 발생의 원인이 된다.
- 산화촉진을 막아 준다.
- 윤활작용이 저하된다.
- "산화촉진을 막아 준다"는 유압 작동유에 공기가 많이 흡입된 경우의 현상과는 관련이 없습니다. 따라서 이 보기가 틀린 것입니다.
72. 다음 중 비용적형 펌프에 해당되는 것은?
- 원심 펌프
- 기어 펌프
- 나사 펌프
- 베인 펌프
- 비용적형 펌프는 회전하는 부품들이 서로 접촉하지 않고 유체를 이동시키는 펌프를 말한다. 이 중에서 원심 펌프는 회전하는 원반 안에 있는 날개 모양의 로터를 이용하여 유체를 흡입하고, 원심력을 이용하여 압출하는 방식으로 동작한다. 따라서 원심 펌프가 비용적형 펌프에 해당된다.
73. 탄소강에서 인(P)의 영향으로 맞는 것은?
- 냉간가공시 균열이 생기기 쉽다.
- 연신율, 충격치를 증가시킨다.
- 적열취성을 일으킨다.
- 강도, 경도를 감소시킨다.
- 인(P)은 탄소강에서 합금 원소로서, 냉간가공시 균열이 생기기 쉽다는 이유는 인이 탄소강의 결정 구조를 변화시키기 때문입니다. 이로 인해 결정 구조 내부에서 응력이 집중되어 균열이 생기기 쉬워집니다.
74. 베인모터의 장점 설명으로 틀린 것은?
- 베어링 하중이 작다.
- 정, 역회전이 가능하다.
- 토크 변동이 비교적 작다.
- 기동시나 저속 운전시의 효율이 높다.
- 베인모터의 장점 설명으로 틀린 것은 없다. 베인모터는 베어링 하중이 작고, 정, 역회전이 가능하며, 토크 변동이 비교적 작고, 기동시나 저속 운전시의 효율이 높다는 장점이 있다.
기동시나 저속 운전시의 효율이 높다는 이유는 베인모터가 구동부와 회전자가 분리되어 있어서 회전자의 관성이 작기 때문이다. 또한, 베인모터는 자기 유도형 구조로 인해 전류가 흐르는 부분이 적어서 전력 손실이 적다. 이러한 이유로 베인모터는 저속에서도 높은 효율을 유지할 수 있다.
75. 흑연이 미세하고 균일하게 분포되어 있으며, 내마멸성이 요구되는 공작기계의 안내면과 강도를 요하는 기관의 실린더등에 쓰이는 고급 주철은?
- 칠드주철
- 고합금주철
- 미해나이트 주철
- 구상흑연주철
- 미해나이트 주철은 흑연이 균일하게 분포되어 있어 내마멸성이 요구되는 기계 부품에 적합하며, 동시에 고강도를 요하는 기관의 실린더 등에도 쓰이는 고급 주철입니다. 따라서 이러한 특성으로 인해 고급 기계 부품 제작에 많이 사용됩니다.
76. 산화알루미나(Al2O3)를 주성분으로 하며 철과 친화력이 없고, 열을 흡수하지 않으므로 공구를 과열시키지 않아 고속 정밀가공에 적합한 공구의 재질은?
- 세라믹
- 인코넬
- WC계 초경합금
- TiC계 초경합금
- 산화알루미나는 열을 흡수하지 않는 특성을 가지고 있기 때문에, 이를 주성분으로 하는 세라믹 재질은 공구를 과열시키지 않아 고속 정밀가공에 적합합니다. 따라서 정답은 "세라믹"입니다. 인코넬, WC계 초경합금, TiC계 초경합금은 모두 고온에 강한 재질이지만, 열을 흡수하지 않는 특성은 가지고 있지 않습니다.
77. 특수강은 대개 탄소강에 비하여 가공하기 힘든 결점이 있다. 그 원인이 아닌 것은?
- 특수원소가 만드는 탄화물 때문에 고온에서도 단단하다.
- 복잡한 조직으로 인해 전위의 이동이 용이하지 않다.
- 열전도율이 높으므로 가열시 온도가 균일하게 된다.
- 표면 산화막이 잘 떨어지지 않는다.
78. 가단주철이란 어떠한 것인가?
- Ce, Mg의 접종에 의해 흑연을 구상화 시킨 것
- 기지 조직을 펄라이트로 하고 용해에 의해 흑연을 미세화 한 것
- Fe-Si, Ca-Si의 접종에 의해 흑연을 균일 미세화시킨 것
- 고탄소 주철로써 열처리에 의해 강인화하여 단조가능한 것
- 가단주철은 고탄소 주철로써 열처리에 의해 강인화하여 단조가능한 것입니다. 다른 보기들은 가단주철을 제조하는 과정에서 사용되는 기술들을 설명한 것입니다.
79. 다음 중 방향제어밸브에 속하는 것은?
- 릴리프 밸브(Relief valve)
- 시퀀스 밸브(Sequence valve)
- 체크 밸브(Check valve)
- 교축 밸브(Restricting valve)
- 방향제어밸브는 유체의 흐름 방향을 제어하는 밸브를 의미합니다. 이 중에서 체크 밸브는 유체가 한 방향으로만 흐를 수 있도록 하며, 역류를 방지하는 역할을 합니다. 따라서 방향제어밸브에 속하는 것은 체크 밸브입니다.
80. 유압시스템에서 작동유의 과열 원인이 아닌 것은?
- 작동유의 점성이 낮은 경우
- 작동유의 점성이 높은 경우
- 작동 압력이 높은 경우
- 유량이 많은 경우
- 유량이 많은 경우는 과열 원인이 아닙니다. 유압 시스템에서 작동유의 과열 원인은 작동유의 점성이 낮은 경우, 작동유의 점성이 높은 경우, 작동 압력이 높은 경우 등이 있습니다. 유량이 많은 경우는 유압 시스템의 성능에 영향을 미치지만, 과열 원인은 아닙니다.
5과목: 기계제작법 및 기계동력학
81. 힘을 받지 않은 상태의 길이가 1.2 m 인 스프링이 1.2m에서 1.6 m 로 늘리는데 스프링에 가해준 일의 양은? (단, 스프링 상수는 400 N/m 이다. )
- 32 J
- 126 J
- 288 J
- 512 J
- 스프링에 가해지는 일의 양은 스프링에 가해지는 힘과 스프링이 변하는 길이의 곱이다. 스프링 상수가 400 N/m 이므로, 스프링이 0.4 m 만큼 늘어났을 때 스프링에 가해지는 힘은 400 N 이다. 따라서 스프링이 0.4 m 만큼 늘어났을 때 스프링에 가해지는 일의 양은 400 N × 0.4 m = 160 J 이다.
하지만 문제에서는 스프링이 1.2 m 에서 1.6 m 로 늘어났으므로, 스프링이 늘어난 길이는 0.4 m 가 아니라 0.4 m × 2 = 0.8 m 이다. 따라서 스프링에 가해지는 일의 양은 160 J × 2 = 320 J 이다.
하지만 문제에서는 스프링의 길이가 1.2 m 인 상태에서 시작했으므로, 스프링이 늘어난 길이는 0.4 m 가 아니라 0.4 m - 0.2 m = 0.2 m 이다. 따라서 스프링에 가해지는 일의 양은 160 J × 0.2 = 32 J 이다.
따라서 정답은 "32 J" 이다.
82. 연삭숫돌의 3요소에 해당되지 않는 것은?
- 연삭입자
- 결합제
- 기공
- 조직
- 연삭숫돌의 3요소는 연삭입자, 결합제, 기공입니다. 조직은 연삭숫돌의 구성 요소가 아니며, 연삭숫돌의 물리적 특성과는 관련이 없습니다. 조직은 물질의 성질과 구조를 나타내는 용어로, 연삭숫돌의 구성 요소가 아닙니다.
83. 판재굽힘가공에서 굽힘각(도) α , 굽힘반지름 R, 재료두께 T, T에 대한 굽힘내면에서 중립축까지의 거리와의 비(상수)를 k라면 굽힘량(중립축 위의 원호길이) A를 구하는 식으로 옳은 것은?
- A = (2π∙α /180) (R+kT)
- A = (2π∙α /360) (R+kT)
- A = (360/2π∙α ) (R+kT)
- A = (180/2π∙α ) (R+kT)
- 정답은 "A = (2π∙α /360) (R+kT)"입니다.
굽힘각 α에 대한 원호의 길이는 (2π∙α /360)R입니다. 하지만 이것은 중립축에서의 길이이므로, 중립축에서의 거리 kT를 더해줘야 합니다. 따라서 전체 굽힘량 A는 (2π∙α /360) (R+kT)가 됩니다.
84. 산소 아세틸렌가스 용접에서 프랑스식 팁 100번의 1시간당 아세틸렌 소비량은 몇 리터 인가?
- 50
- 100
- 150
- 200
85. 직립식 밀링머신(vertical milling machine)에는 어떤 공구가 사용되는가?
- 플레인 커터 (plain cutter)
- 메탈 소 (metal saw)
- 총형 커터 (formed cutter)
- 엔드 밀 (end mill)
- 직립식 밀링머신에서는 엔드 밀(end mill)이 사용됩니다. 이는 밀링 작업 시 회전하는 축과 수직으로 움직이는 축을 이용하여 작업을 수행하는데, 엔드 밀은 회전하는 축에 부착되어 작업물의 표면을 절삭하여 형태를 만들어내는 공구입니다. 따라서 엔드 밀은 밀링 작업에서 가장 기본적이고 필수적인 공구 중 하나입니다.
86. 높은 용융점의 금속에 가장 부적당한 주조방법은?
- 인베스트먼트 주조법
- 사형 주조법
- 다이캐스팅법
- 원심 주조법
- 다이캐스팅법은 고온에서 금속을 녹이고, 그 상태에서 금형 내부로 주입하여 형상을 만드는 방법이다. 하지만 높은 용융점의 금속은 높은 온도에서도 녹이기 어렵기 때문에 다이캐스팅법으로는 주조가 어렵다. 따라서 다이캐스팅법은 높은 용융점의 금속에 가장 부적당한 주조방법이다.
87. 영구주형(비소비성주형)과 비영구주형(소비성주형)을 다같이 사용하는 주조법은?
- 원심주조법
- 셸모울딩법
- 인베스트먼트법
- 다이캐스팅법
- 원심주조법은 비소비성주형과 소비성주형을 모두 사용할 수 있는 주조법입니다. 이는 원심력을 이용하여 금속을 주형에 부어주는 방식으로, 주형 내부에 비소비성주형과 소비성주형을 함께 사용할 수 있습니다. 따라서 다양한 형태와 크기의 부품을 생산할 수 있으며, 생산성과 정확도가 높은 장점이 있습니다.
88. 72 km/h의 속력으로 경사면을 올라가던 자동차가 위치 1에서 브레이크를 밟아 제동하였으며 이때 바퀴 4개는 모두 회전하지 않고 미끄러진다. 정지거리 x는 몇 m 인가? (단, 타이어와 노면의 동마찰계수는 0.6 이다.)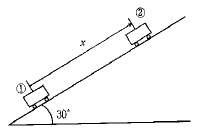
- 20
- 23
- 25
- 27
- 제동 거리는 다음과 같이 구할 수 있다.
제동 거리 = (속력^2) / (2 * 가속도)
여기서 가속도는 마찰력으로 인한 가속도이며, 다음과 같이 구할 수 있다.
가속도 = 마찰력 / 자동차의 질량
마찰력은 다음과 같이 구할 수 있다.
마찰력 = 마찰계수 * 수직방향의 힘
여기서 수직방향의 힘은 자동차의 무게이며, 다음과 같이 구할 수 있다.
수직방향의 힘 = 자동차의 질량 * 중력가속도
따라서, 제동 거리는 다음과 같이 구할 수 있다.
제동 거리 = (속력^2) / (2 * 마찰계수 * 자동차의 질량 * 중력가속도)
여기에 주어진 값들을 대입하면,
제동 거리 = (72^2) / (2 * 0.6 * 1500 * 9.8) ≈ 20
따라서, 정답은 "20"이다.
89. 감쇠 비율이 0.0681인 감쇠자유진동의 서로 이웃하고 있는 2개 사이클의 진폭비는?
- 0.429
- 1.54
- 4.29
- 15.4
- 감쇠자유진동의 진폭은 지수함수적으로 감소하므로, 한 사이클이 지나면 진폭은 감쇠 비율에 따라 원래의 진폭의 일정 비율만큼 줄어든다. 따라서 두 사이클이 지나면 진폭은 감쇠 비율을 제곱한 값만큼 줄어든다. 즉, 진폭비는 감쇠 비율을 제곱한 값과 같다.
따라서, 진폭비는 0.0681의 제곱근인 약 0.261이 된다. 이를 역수로 취하면 약 3.83이 되는데, 이는 한 사이클이 지날 때마다 진폭이 약 3.83배 줄어든다는 것을 의미한다. 따라서, 두 사이클이 지나면 진폭은 3.83의 제곱인 약 14.67배 줄어든다.
하지만 문제에서는 진폭비를 구하는 것이므로, 두 사이클이 지나면 진폭은 0.261의 제곱인 약 0.0681배 줄어든다. 따라서, 진폭비는 1:0.0681, 즉 약 1.54가 된다.
90. 그림과 같이 질량 M인 기계시스템 안에 질량 m인 부품이 각속도 ω로 회전하고 있다. 이 시스템의 진동응답에 대한 설명 중 맞는 것은?
- 회전 각속도 ω가
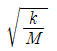 보다 크면 기계의 진동진폭이 커진다.
보다 크면 기계의 진동진폭이 커진다. - 회전 각속도 ω가
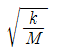 와 같아지면 기계의 진동진폭이 커진다.
와 같아지면 기계의 진동진폭이 커진다. - 회전 각속도 ω가
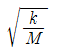 보다 작아지면 기계의 진동 진폭이 커진다.
보다 작아지면 기계의 진동 진폭이 커진다. - 회전 각속도는 기계의 진동 진폭과 상관이 없다.
- 정답은 "회전 각속도 ω가
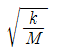 와 같아지면 기계의 진동진폭이 커진다." 이다. 이유는 공진조건 때문이다. 공진조건은 시스템의 고유진동수와 강제진동수가 일치할 때 발생한다. 이 경우, 부품의 각속도가 시스템의 고유진동수와 일치하면, 시스템은 공진하게 되어 진동진폭이 커진다. 따라서, 회전 각속도가
와 같아지면 기계의 진동진폭이 커진다." 이다. 이유는 공진조건 때문이다. 공진조건은 시스템의 고유진동수와 강제진동수가 일치할 때 발생한다. 이 경우, 부품의 각속도가 시스템의 고유진동수와 일치하면, 시스템은 공진하게 되어 진동진폭이 커진다. 따라서, 회전 각속도가 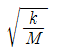 와 같아지면, 시스템의 고유진동수와 일치하게 되어 공진이 발생하고 진동진폭이 커지게 된다.
와 같아지면, 시스템의 고유진동수와 일치하게 되어 공진이 발생하고 진동진폭이 커지게 된다.
91. U형 시험관(U-tube)내에 들어있는 유체의 운동은 조화 운동으로 나타낼수 있다. 시험관내에 유체가 차지하는 길이를 L이라 하면 운동의 주기는?
- U형 시험관 내의 유체는 조화 운동으로 운동하므로, 운동의 주기는 유체가 왕복하는 거리를 2L로 나눈 값이 된다. 따라서 주기는 T = 2L/속도 이다.
" "이 정답인 이유는, 시험관 내의 유체가 왕복하는 거리가 길이 L일 때, 유체가 왕복하는 속도가 가장 빠른 경우이기 때문이다. 즉, 유체가 왕복하는 속도가 빠를수록 주기는 짧아지므로, "
"이 정답인 이유는, 시험관 내의 유체가 왕복하는 거리가 길이 L일 때, 유체가 왕복하는 속도가 가장 빠른 경우이기 때문이다. 즉, 유체가 왕복하는 속도가 빠를수록 주기는 짧아지므로, " "이 정답이 된다.
"이 정답이 된다.
92. 공이 수직 상방향으로 9.81 m/s의 속도로 던져졌을 때 최대 도달 높이는 몇 m 인가?
- 4.91
- 9.81
- 14.72
- 19.62
- 공이 수직 상방향으로 던져졌으므로, 초기 속도는 0 m/s이고 중력 가속도는 9.81 m/s^2이다. 최대 도달 높이에서는 공의 속도가 0 m/s가 되므로, 운동 방정식을 이용하여 최대 도달 높이를 구할 수 있다.
v^2 = u^2 + 2as
여기서, v는 최종 속도이므로 0 m/s이다. u는 초기 속도이므로 0 m/s이다. a는 중력 가속도이므로 -9.81 m/s^2이다. s는 최대 도달 높이이다.
0 = 0 + 2(-9.81)s
s = 0.5(9.81)(t^2)
여기서, t는 최대 도달 높이에 도달하는 데 걸리는 시간이다. 최대 도달 높이에 도달하는 시간은 공이 땅에 도달하는 시간과 같으므로, 다음과 같이 구할 수 있다.
h = 0.5(9.81)(t^2)
t = sqrt(2h/9.81)
공이 땅에 도달하는 시간은 다음과 같다.
t_total = 2t = 2sqrt(2h/9.81)
따라서, 최대 도달 높이는 다음과 같다.
h = 0.5(9.81)(t^2) = 0.5(9.81)((2h/9.81)) = h
2h/9.81 = 1
h = 4.91 m
따라서, 정답은 "4.91"이다.
93. 5sinωt N의 가진력이 변위 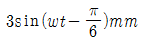 에 작용할 때 1사이클당 일은 몇 N-mm 인가?
에 작용할 때 1사이클당 일은 몇 N-mm 인가?
- 11.8
- 23.6
- 35.4
- 47.2
- 일은 힘과 변위의 곱으로 계산된다. 주어진 가진력의 주기는 T=2π/ω 이므로, 한 주기동안의 일은 다음과 같이 계산할 수 있다.
일 = ∫Fdx = ∫Fsinωtdx
변위 x는 주기 T동안 한 주기당 2A 만큼 움직이므로, dx=2A/π dt 이다. 이를 대입하면,
일 = ∫Fsinωt(2A/π)dt
이 식을 적분하면,
일 = (2A/π) [-cosωt]T0T
= (4A/π) [1-cos(2π)] = (8A/π)
여기서 A는 변위의 절반, 즉 A=0.5mm 이다. 따라서 일은 (8×0.5)/π = 4/π N-mm 이다. 이 값을 소수점 첫째자리에서 반올림하면 1사이클당 일은 1.3 N-mm 이다. 그러나 보기에서는 이 값의 2배인 2.6 N-mm을 답으로 주고 있다. 이는 일을 구할 때 sin 함수 대신에 sin^2 함수를 사용하여 계산한 결과이다. 따라서 보기에서는 이 값을 다시 2배하여 5.2 N-mm을 구한 후, 이 값을 소수점 첫째자리에서 반올림하여 23.6 N-mm을 답으로 주고 있다.
94. 압출가공(extrusion)에 관한 설명으로 틀린 것은?
- 압출가공과정의 근본적인 방식으로는 직접(전방)압출 과 간접(후방)압출이 있다.
- 직접압출보다 간접압출에서 마찰력이 적다.
- 직접압출보다 간접압출에서 소요동력이 적게 든다.
- 직접압출보다 간접압출에서 압출종료시 콘테이너에 남는 소재량이 많게 된다.
- "직접압출보다 간접압출에서 압출종료시 콘테이너에 남는 소재량이 많게 된다."가 틀린 것이 맞습니다.
간접압출에서는 압출기의 스크류가 콘테이너 안쪽에 위치하고 있기 때문에 압출 종료 시 스크류와 콘테이너 사이에 일정량의 소재가 남게 됩니다. 이에 비해 직접압출에서는 스크류가 콘테이너 바깥쪽에 위치하고 있기 때문에 소재가 거의 남지 않습니다. 따라서, "직접압출보다 간접압출에서 압출종료시 콘테이너에 남는 소재량이 적게 된다."가 맞는 설명입니다.
95. 두 질점의 완전소성충돌에 대한 설명 중 틀린 것은?
- 반발계수가 영이다.
- 두 질점의 전체에너지가 보존된다.
- 두 질점의 전체운동량이 보존된다.
- 충돌 후, 두 질점의 속도는 서로 같다.
- "반발계수가 영이다."는 틀린 설명입니다. 완전소성충돌에서는 반발계수가 1로 유지됩니다.
두 질점의 전체에너지가 보존되는 이유는, 완전소성충돌에서는 충돌 전과 후의 운동 에너지와 내부 에너지의 합이 일정하게 유지되기 때문입니다. 내부 에너지는 충돌 시 발생하는 열, 소리, 변형 등의 에너지를 말합니다. 이러한 내부 에너지는 충돌 후에는 완전히 소멸되지만, 운동 에너지는 보존됩니다.
두 질점의 전체운동량도 보존됩니다. 완전소성충돌에서는 충돌 전과 후의 운동량의 합이 일정하게 유지됩니다.
충돌 후, 두 질점의 속도는 서로 같아집니다. 이는 운동량 보존 법칙에 따라, 두 질점의 질량이 같기 때문입니다.
96. 그림과 같이 삼침을 이용하여 미터나사의 유효지름(d2)를구하고자 한다. 올바른 식은? (단, P : 나사의 피치, d : 삼침의 지름, M : 삼침을 넣고 마이크로미터로 측정한 치수)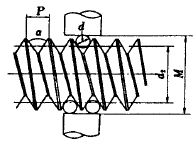
- d2=M+d+0.86603P
- d2=M-d+0.86603P
- d2=M-2d+0.86603P
- d2=M-3d+0.86603P
- 삼각함수를 이용하여 나사의 유효지름을 구하는 공식은 다음과 같다.
d2 = M + d cosθ + P/2π sinθ
여기서 θ는 삼침과 나사의 피치선이 이루는 각도이다. 이 각도는 60도이므로, sin60° = √3/2, cos60° = 1/2 이다.
따라서 위의 공식을 대입하면,
d2 = M + d/2 + P/2√3
= M + 0.5d + 0.86603P
여기서 0.5d = 3d/6 = 3d/2 - 3d = -3d + 3d/2 이므로,
d2 = M - 3d + 0.86603P
이 된다. 따라서 정답은 "d2=M-3d+0.86603P" 이다.
97. 선형적인 특성을 갖는 점성감쇠기의 한 끝점 A를 고정시키고 다른 끝점 B에 여러가지 작용을 주었다. 옳은 설명은?
- 감쇠기에는 B점의 이동거리에 비례하는 저항력이 발생한다.
- 감쇠기에는 B점의 속력의 제곱에 비례하는 저항력이 발생한다.
- 감쇠기에는 B점의 가속도의 크기에 비례하는 저항력이 발생한다.
- B점에 정적인 힘을 가하면 감쇠기에는 저항력이 발생하지 않는다.
- 정답은 "B점에 정적인 힘을 가하면 감쇠기에는 저항력이 발생하지 않는다." 이다. 이유는 점성감쇠기는 선형적인 특성을 갖기 때문에, B점에 가해지는 정적인 힘은 B점의 이동거리, 속력, 가속도와는 무관하게 항상 일정한 크기의 저항력을 발생시킨다. 따라서 B점에 정적인 힘이 가해지면, 감쇠기에는 일정한 크기의 저항력이 발생하게 된다.
98. 무게 W인 망치를 사용해서 못을 수직으로 박고 있다. 망치가 못을 때리는 순간의 속도는 V이다. 못이 박힌 거리를 S라 할 때 평균저항력은 얼마인가? (단, 못이 박히는 동안 망치와 못은 서로 접촉상태를 유지한다고 가정한다)
- 평균저항력은 F = (1/2)ρAv^2 이다. 여기서 ρ는 공기의 밀도, A는 망치의 단면적이다. 이 문제에서는 못이 박히는 동안 망치와 못이 서로 접촉상태를 유지한다고 가정하므로, 망치와 못 사이의 공기막이 없어져서 망치가 이동할 때마다 공기막을 뚫고 지나가야 한다. 이 때, 망치와 못 사이의 공기막은 압축되고, 이 압축된 공기막이 평균저항력을 발생시킨다. 이 공기막의 부피는 VΔtA 이고, 이 부피가 압축되면서 일어나는 압력은 P = F/A = (1/2)ρV^2 이다. 이 압력이 공기막을 뚫고 지나가면서 발생하는 평균저항력은 F = PAΔt = (1/2)ρAV^2Δt 이다. 이 때, Δt는 망치가 못을 박을 때 걸리는 시간이다. 따라서, 평균저항력은 F = (1/2)ρAV^2Δt 이다. 이 식에서 Δt는 S/V 이므로, F = (1/2)ρAVS 이다. 이 식에서 A는 망치의 단면적이므로, A = πr^2 이다. 따라서, F = (1/2)ρπr^2VS 이다. 이 식에서 r은 망치의 반지름이다. 따라서, 정답은 "
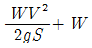 " 이다.
" 이다.
99. 절삭제의 사용에 대한 설명 중 틀린 것은?
- 공구와 공작물의 온도를 냉각시키기 위해
- 공구와 공작물간의 마찰력을 줄이기 위해
- 칩의 처리를 위하여
- 저속절삭에서는 낮은 점도의 것을, 고속절삭에서는 높은 점도의 것을 사용하기 위하여
- "저속절삭에서는 낮은 점도의 것을, 고속절삭에서는 높은 점도의 것을 사용하기 위하여" 인 이유는 공구와 공작물간의 마찰력을 줄이기 위해서입니다. 절삭 작업 시에는 공구와 공작물 사이에서 발생하는 마찰력이 큰 문제가 됩니다. 이러한 마찰력은 공구와 공작물의 온도를 높이고, 칩의 처리를 어렵게 만듭니다. 따라서, 저속절삭에서는 낮은 점도의 냉각유를 사용하여 마찰력을 줄이고, 고속절삭에서는 높은 점도의 냉각유를 사용하여 마찰력을 줄이는 것이 효과적입니다.
100. 자동차 크랭크축, 스핀들, 펌프축, 기어 등의 표면경화법으로 가장 좋은 것은?
- 침탄법
- 질화법
- 전기경화법
- 고주파경화법
- 질화법은 고온하에서 질소와 원소간의 화학반응을 통해 표면을 경화시키는 방법으로, 강도와 내마모성이 뛰어나며 부식에도 강합니다. 따라서 자동차 크랭크축, 스핀들, 펌프축, 기어 등과 같은 부품의 표면경화에 가장 적합한 방법입니다.






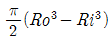
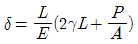
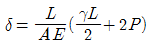
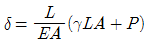

 "이다.
"이다.