1과목: 과목 구분 없음
1. 100[N]의 하중을 50[cm] 들어 올리는 데, 8[초]동안 15[W]의 동력이 작용했다면, 이 전동 잭의 효율[%]은?
- 41.7
- 33.3
- 44.5
- 39.7
2. 두께가 t0, 사용압력이 p0, 내경이 r0인 원통형 압력용기(A)가 있다. 이 압력용기와 동일재료로 강판의 두께를 2배, 원통의 반경을 2배로 하여 동일한 형태의 압력용기(B)를 제작하고, 사용압력을 2배로 할 때 압력용기(B)의 최대전단응력 크기는 압력용기(A)의 몇 배인가? (단, t0/r0≪1이라고 가정한다)
- 8 배
- 4 배
- 2 배
- 1 배
3. 마찰차에 대한 설명으로 옳지 않은 것은?
- 마찰차는 원통마찰차, 홈마찰차, 원추마찰차, 무단변속마찰차로 분류할 수 있다.
- 마찰차는 전달해야 될 힘이 그다지 크지 않으며, 속비가 중요하지 않을 경우 사용한다.
- 마찰계수를 크게 하기 위해 종동차(피동차)를 원동차(구동차)보다 연질의 재료를 사용한다.
- 보통 원동차 표면에 목재, 고무, 가죽, 특수 섬유질 등을 라이닝하여 사용한다.
4. 직경 D1=200 [mm], D2=400 [mm]이고, 잇수 z1=50, z2=100인 한 쌍의 평기어가 있다. 속도계수는 0.4, 접촉면응력계수 k=0.075 [kgf/mm2], 이의 폭 b=80 [mm]라 하면, 기어에 걸리는 회전력[kgf]은?
- 320
- 640
- 800
- 1,600
5. 회전수 1,000 [rpm]으로 10 [kW]의 동력을 전달하는 단판 클러치의 내경이 100 [mm], 외경이 200 [mm], 마찰계수가 0.2일 때, 클러치를 축방향으로 미는 힘[kgf]은?
- 162.3
- 324.7
- 477.5
- 649.3
6. 고속 회전 시 미끄러짐을 방지하기 위하여 스러스트 볼베어링에 예압(preload)을 가하게 된다. 운전속도(N)가 제한속도(Nmax)의 20%인 경우 기본 정 정격하중(C0)의 몇 배로 예압해야 하는가?
- 1/100 배
- 1/500 배
- 1/1000 배
- 1/2500 배
7. 벨트의 평행걸기(open belting) 시 축간 중심거리는 1,000 [mm], 원동차의 지름은 400 [mm], 종동차의 지름은 300 [mm]이다. 벨트의 길이에 가장 가까운 값[mm]은?
- 3,060
- 3,100
- 3,140
- 3,180
8. 자중을 무시할 수 있는 길이 L인 원형 단면 실축(탄성 계수 E)이 단순지지되어 있다. 이 축의 중앙에 하중 W인 회전체가 설치되어 있을 때, 위험속도(N[rpm])가 되는 축의 지름은? (단, g는 중력가속도이다)
9. 굽힘모멘트와 토크를 동시에 받는 축의 인장응력은 90 [MPa], 전단응력은 60 [MPa]이다. 허용인장응력을 110 [MPa], 허용전단응력을 80 [MPa]이라 할 때, 다음 설명 중 옳지 않은 것은?
- 최대주응력설에 의하면, 이 축은 안전하지 않다.
- 최대전단응력설에 의하면, 이 축은 안전하지 않다.
- 전단변형에너지설(von Mises yield criteria)에 의하면, 이 축은 안전하지 않다.
- 단순인장응력상태에서는 최대주응력설에 의한 파손조건과 전단변형에너지설에 의한 파손조건이 같아진다.
10. 다음 그림에서 벨트 풀리 1(I1)에 700 [PS]이 전달되고, 이 동력은 풀리 2(I2)에 300 [PS], 풀리 3(I3)에 400 [PS]으로 나누어 전달된다. 풀리 2의 좌측과 우측의 축에 걸리는 전단응력이 같아지도록 설계한다면, d1/d2은? (단, 자중 및 굽힘하중에 의한 전단응력은 무시한다)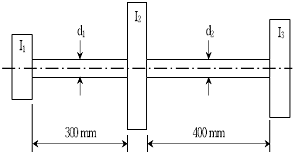
11. 유니파이 보통나사 3/4-10 UNC의 피치[mm]는?
- 0.75
- 10
- 19.05
- 2.54
12. 이의 수 16개인 피니언이 이의 수 40개인 기어를 구동시키는 평기어쌍이 있다. 모듈은 12 [mm], 이끝높이와 이뿌리높이는 각각 12 [mm], 15 [mm]이고, 압력각이 20°일 때, 원주피치[mm] 및 중심거리[mm]는?
- 원주피치[mm]: 37.7, 중심거리[mm]: 336
- 원주피치[mm]: 37.7, 중심거리[mm]: 672
- 원주피치[mm]: 75.4, 중심거리[mm]: 336
- 원주피치[mm]: 75.4, 중심거리[mm]: 672
13. 안지름이 312 [mm]인 이음매 없는 강관에 유량이 약 0.23 [m3/s], 수압이 2 [MPa]인 유체가 흐를 때, 이에 적합한 강관의 바깥지름 [mm]은? (단, 허용인장응력은 78 [MPa], 부식여유는 1 [mm], 평균유속은 3 [m/s]로 한다)
- 322
- 350
- 344
- 336
14. 합금강에서 합금원소의 영향으로 옳지 않은 것은?
- 몰리브덴(Mo)은 고온에서 강도나 경도의 저하가 적으며, 담금질성을 증가시킨다.
- 텅스텐(W)은 탈산 및 탈질 작용이 강하며, 결정립을 미세화 한다.
- 크롬(Cr)은 내마모성과 내식성을 증가시키며, 4 [%] 이상 함유될 경우 단조성이 떨어진다.
- 니켈(Ni)은 저온에서 내충격성을 향상시킨다.
15. 대표적인 관이음 방법인 플랜지를 설계할 때, 플랜지 면에 수직으로 작용하는 전하중이 P이면 플랜지의 두께는 t0이다. 동일 조건에서 압력이 두 배가 된다면, 플랜지의 최소두께는 t0의 몇 배로 설계해야 하는가?
- 1.5
- 2
- √2
- 4
16. 그림과 같은 내부확장식 드럼 브레이크로 363 [N-m]의 토크를 제동하려고 한다. 브레이크 슈에 작용하는 힘 F [kN]는 최소 얼마이어야 하는가? (단, 그림에서 a=110 [mm], b=55 [mm], c=50 [mm], D=140 [mm]이고, 마찰계수는 0.3이다)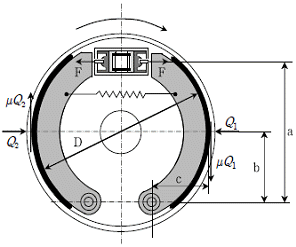
- 1
- 2
- 3
- 4
17. 피로파손 및 내구선도에 대한 설명으로 옳지 않은 것은?
- S-N곡선(피로한도 곡선)이 가로축과 평행하게 되는 시작점에서의 양진응력의 크기, 즉 응력진폭을 피로한도라고 한다.
- 모든 금속재료는 N=106~107정도에서 명백한 피로한도를 보이며, 이 피로한도보다 낮은 응력진폭에서는 피로파괴되지 않는 것으로 간주하여 설계한다.
- 변동응력이 작용하는 경우에는, 가로축을 평균응력(σm), 세로축을 응력진폭으로 하는 내구선도를 작성하고 작용응력이 안전영역 이내에 있도록 설계하여야 한다.
- 조더버그(Soderberg)선도는 내구선도의 세로축 절편을 피로한도, 가로축 절편을 항복강도로 하는 두 점을 직선으로 연결한 내구선도를 말한다.
18. 판두께 14 [mm], 리벳의 지름 22 [mm], 피치 54 [mm]로 리벳 중심에서 판 끝까지 1열 리벳 겹치기 이음하여 한 피치당 인장하중 1,350 [kgf]이 작용할 때, 판에 생기는 인장응력[kgf/mm2]은?
- 2.0
- 2.5
- 3.0
- 3.5
19. 토크 T를 받고 있는 직경 D인 원형축의 한쪽 끝이 벽에 목두께 a로 필릿 용접되어 있을 때, 목두께에 작용하는 최대 전단응력을 구하는 식은?
20. 그림과 같이 스프링 상수 1.5 × 109[ N/m]인 볼트로 스프링 상수 1 × 109 [N/m]인 결합체를 초기 체결력 10 [kN]으로 체결한 후, 외부로부터 10 [kN]의 인장하중이 작용하였을 때, 결합체에 작용하는 하중[kN]은? (단, +하중은 인장하중, -하중은 압축하중이다)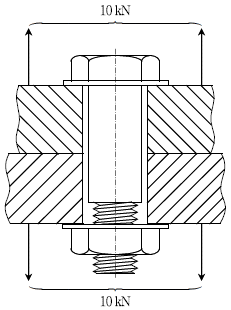
- +4
- -4
- +6
- -6






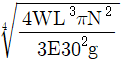
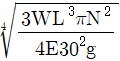
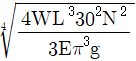
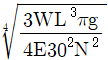
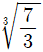
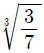
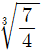
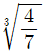
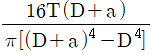
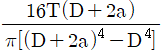
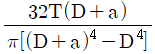
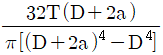
그리고 이 전동 잭이 실제로 일을 하는데 사용한 에너지는 하중을 들어 올리는 데 사용된 에너지와 같습니다. 하중을 50[cm] 들어 올리는 데 필요한 일은 100[N] x 50[cm] = 5000[J] 입니다.
따라서 이 전동 잭의 효율은 (실제로 사용된 에너지 / 사용자가 공급한 에너지) x 100 으로 계산할 수 있습니다. 여기서 사용자가 공급한 에너지는 120[J] 이므로, 효율은 (5000[J] / 120[J]) x 100 = 41.7% 입니다.
따라서 정답은 "41.7" 이 됩니다.