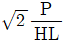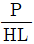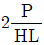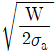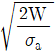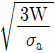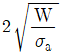9급 지방직 공무원 기계설계 필기 기출문제복원 (2013-08-24)

9급 지방직 공무원 기계설계
(2013-08-24 기출문제)

목록

1. 후크의 법칙에 대한 설명으로 옳은 것은?

  1. 탄성계수의 값은 모든 재료에서 동일하다.
  2. 비례한도 이내에서 응력과 변형률은 비례한다.
  3. 비례한도 이내에서 변형량과 단면적은 비례한다.
  4. 비례한도 이내에서 변형량과 탄성계수는 비례한다.
(정답률: 86%)
  • 후크의 법칙은 일정한 영역에서 재료의 응력과 변형률이 비례한다는 법칙입니다. 이는 재료가 탄성 범위 내에서 변형되는 경우에 해당하며, 이 범위를 비례한도라고 합니다. 따라서, 비례한도 이내에서 응력과 변형률은 비례하게 됩니다. 이는 재료의 탄성계수와도 관련이 있으며, 탄성계수는 모든 재료에서 동일하다는 것이 후크의 법칙의 또 다른 특징입니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

2. 회전하는 축에 2개의 회전체를 설치하였다. 축의 자중만에 의한 위험속도는 N0[rpm], 각 회전체를 단독으로 축에 설치했을 경우 축의 자중을 무시한 위험속도는 각각 N1[rpm], N2[rpm]이다. 이때, 축의 위험속도 Nc[rpm]를 구하기 위한 던커레이(Dunkerley) 공식은?

  1. Nc=N0+N1+N2
(정답률: 96%)
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

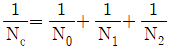
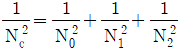
3. 유체를 한 방향으로만 흐르도록 하고 역류를 방지할 목적으로 사용하는 밸브는?

  1. 체크 밸브
  2. 슬루스 밸브
  3. 스톱 밸브
  4. 안전 밸브
(정답률: 97%)
  • 체크 밸브는 유체가 한 방향으로만 흐르도록 하고 역류를 방지하기 위해 사용됩니다. 이는 밸브 내부에 있는 이동 가능한 디스크나 플랩이 유체의 흐름 방향에 따라 열리고 닫힘으로써 구현됩니다. 따라서 유체가 한 방향으로만 흐르도록 하고 역류를 방지할 수 있습니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

4. 다음 설명에 해당하는 커플링은?

  1. 올덤 커플링
  2. 슬리브 커플링
  3. 플랜지 커플링
  4. 유니버설 커플링
(정답률: 78%)
  • 이 커플링은 두 축이 서로 다른 방향으로 회전할 수 있도록 구성되어 있어서, 유니버설 커플링이라고 부릅니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

5. 두께 2 [mm]인 강판 2장을 지름 20 [mm]인 리벳을 이용하여 2줄 겹치기 이음을 하고자 한다. 1 피치 내의 하중은 20 [kN]이고 판효율이 60%라면 피치는 몇 [mm]인가?

  1. 40
  2. 50
  3. 60
  4. 70
(정답률: 84%)
  • 리벳 1개 당 하중은 10 [kN]이므로, 1줄에는 2개의 리벳이 필요하다. 따라서 2줄에는 총 4개의 리벳이 필요하다.

    판효율이 60%이므로, 실제로 전달되는 하중은 20 [kN] x 0.6 = 12 [kN]이다.

    리벳 1개가 전달하는 하중은 전체 하중의 1/4이므로, 1개의 리벳에 작용하는 하중은 12 [kN] / 4 = 3 [kN]이다.

    리벳의 단면적은 다음과 같다.

    A = (π/4) x d^2
    = (π/4) x 20^2
    = 314 [mm^2]

    강판의 두께가 2 [mm]이므로, 리벳이 두께 방향으로 작용하는 면적은 2 x 20 = 40 [mm^2]이다.

    따라서, 리벳 1개가 버틸 수 있는 하중은 다음과 같다.

    σ = F/A
    F = σ x A
    = 235 [MPa] x 40 x 10^-6 [m^2]
    = 9.4 [kN]

    리벳 1개가 버틸 수 있는 하중은 9.4 [kN]이므로, 1줄에는 2개의 리벳이 필요하다. 따라서, 2줄에는 총 4개의 리벳이 필요하며, 피치는 리벳 2개 사이의 거리이므로 다음과 같이 계산할 수 있다.

    20 [mm] x 2 / 4 = 10 [mm]

    따라서, 정답은 "50"이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

6. 그림과 같이 하중 P가 용접선에 평행하게 작용할 때, 용접부에 발생하는 최대 전단응력은?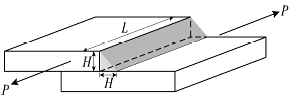

(정답률: 76%)
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

7. 벨트전동에서 인장측 장력이 이완측 장력의 3배이고 벨트의 유효장력이 100 [kgf]일 때, 인장측 장력[kgf]은? (단, 원심력의 영향은 무시함)

  1. 50
  2. 67
  3. 150
  4. 200
(정답률: 68%)
  • 벨트전동에서 인장측 장력과 이완측 장력은 벨트가 회전하는 방향과 반대 방향으로 작용합니다. 따라서 인장측 장력이 이완측 장력의 3배라면, 인장측 장력은 이완측 장력의 3배인 300 [kgf]이 됩니다.

    하지만, 벨트의 유효장력이 100 [kgf]이므로, 인장측 장력은 유효장력을 초과할 수 없습니다. 따라서 인장측 장력은 100 [kgf]이 됩니다.

    따라서, 정답은 100 [kgf]이 아닌 "150"입니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

8. 그림과 같은 단식 블록 브레이크에서 드럼의 지름이 360 [mm]이고 브레이크 레버의 조작력 F가 200 [N]일 때, 드럼이 우회전할 경우 제동 토크[N·mm]는? (단, l1＝500 [mm], l2＝190 [mm], l3＝50 [mm], 마찰계수 μ＝0.2 )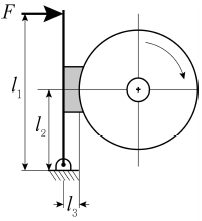

  1. 9,000
  2. 10,000
  3. 18,000
  4. 20,000
(정답률: 85%)
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

9. 내경과 외경의 비가 2인 중공축에 작용할 수 있는 허용 비틀림 모멘트는 T이다. 만약 내경을 고정한 상태에서 내경과 외경의 비를 4로 설계할 경우, 허용 비틀림 모멘트는? (단, 축 재료의 허용응력은 동일함)

  1. 4.5T
  2. 6.5T
  3. 8.5T
  4. 10.5T
(정답률: 71%)
  • 내경과 외경의 비가 2일 때, 내경과 외경의 단면적 비는 1:3이 된다. 따라서 내경을 고정한 상태에서 외경을 4로 설계하면, 외경의 단면적은 내경의 4배가 되므로 내경과 외경의 단면적 비는 1:12가 된다.

    비틀림 모멘트는 단면의 형상과 크기에 따라 달라지며, 단면의 비틀림 강도에 따라 비례한다. 내경과 외경의 비가 2일 때의 비틀림 모멘트를 T라고 하면, 내경과 외경의 비가 4일 때의 비틀림 모멘트는 내경과 외경의 단면적 비인 1:12에 비례하여 12배가 된다. 따라서 허용 비틀림 모멘트는 12T가 된다.

    정답은 "8.5T"이다. 이는 축 재료의 허용응력이 동일하다는 가정 하에, 내경과 외경의 비를 4로 설계할 경우에도 축이 견딜 수 있는 최대 비틀림 모멘트가 T라는 것을 의미한다. 따라서 내경과 외경의 비가 4일 때의 허용 비틀림 모멘트는 T의 값인 1배가 된다. 이에 따라 내경과 외경의 비가 4일 때의 허용 비틀림 모멘트는 8.5T가 된다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

10. 일정한 축방향 하중이 작용하는 원통형 코일스프링에서 소선의 지름과 스프링 전체의 평균지름을 모두 2배로 증가시킬 경우 스프링의 처짐량은 몇 배인가?

  1. 0.5
  2. 1
  3. 2
  4. 4
(정답률: 84%)
  • 스프링의 처짐량은 스프링 상수와 하중의 비례 관계에 있으므로, 스프링 상수는 변하지 않는다고 가정할 수 있다. 따라서 스프링의 처짐량은 하중과 스프링 길이의 제곱의 역수에 비례한다.

    지름이 2배로 증가하면 스프링 길이는 2배가 아닌 4배가 된다. 따라서 스프링의 처짐량은 (2/4)^2 = 0.25배가 된다. 하지만 문제에서는 평균지름도 2배로 증가했으므로, 처짐량은 0.25배에 2를 곱한 0.5배가 된다. 따라서 정답은 "0.5"이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

11. 볼트에 축방향의 정하중 W[kgf]가 작용할 때, 허용인장응력 σa[kgf/mm2]를 만족시키기 위한 볼트의 최소 바깥지름 d [mm]는? (단, 골지름 d1=0.8d)

(정답률: 70%)
  • 볼트의 최소 바깥지름은 다음과 같이 구할 수 있다.

    σa = W / (π/4 × d2) ≤ σallow

    d ≥ √(W / (π/4 × σallow))

    여기서 골지름 d1=0.8d 이므로,

    d1 = 0.8 × d ≥ 0.8 × √(W / (π/4 × σallow))

    따라서, 답은 "" 이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

12. 미터나사 M 30 × 3에 대한 설명으로 옳은 것은?

  1. 미터 보통 나사 유효지름 30 [mm], 산수 3
  2. 미터 가는 나사 바깥지름 30 [mm], 산수 3
  3. 미터 보통 나사 유효지름 30 [mm], 피치 3 [mm]
  4. 미터 가는 나사 바깥지름 30 [mm], 피치 3 [mm]
(정답률: 84%)
  • 정답은 "미터 가는 나사 바깥지름 30 [mm], 피치 3 [mm]"입니다.

    미터나사는 나사의 규격을 나타내는 표준화된 표기법 중 하나입니다. M은 미터를 의미하며, 숫자는 바깥지름을 나타냅니다. 따라서 "미터 가는 나사 바깥지름 30 [mm]"라는 표현은 나사의 바깥지름이 30mm라는 것을 의미합니다.

    또한, 피치는 나사의 간격을 나타내는 값으로, 나사가 한 번 회전할 때 나아가는 거리를 의미합니다. 따라서 "피치 3 [mm]"라는 표현은 나사의 간격이 3mm라는 것을 의미합니다.

    반면, "미터 보통 나사 유효지름 30 [mm], 산수 3"라는 표현은 유효지름과 산수라는 개념을 사용하고 있으며, 미터나사의 표기법과는 다른 표기법입니다. 따라서 이는 옳지 않은 설명입니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

13. 삼각나사에 작용하는 축방향 하중을 Q, 마찰계수를 μ, 나사산의 각을 2β라고 할 때, 나사면에 발생하는 마찰력은?

  1. μQ
  2. μQcosβ
  3. μQ/cosβ
  4. μQ/sinβ
(정답률: 79%)
  • 삼각나사에 작용하는 축방향 하중 Q는 나사면에 수직 방향으로 작용하며, 이에 따라 마찰력이 발생합니다. 마찰력은 마찰계수 μ와 수직 방향의 하중 Q에 비례합니다. 따라서 마찰력은 μQ로 표현할 수 있습니다.

    하지만, 이 문제에서는 나사산의 각도 2β가 고려되어야 합니다. 나사면에 작용하는 마찰력은 수직 방향의 하중 Q을 나사산의 각도 2β에 대한 삼각함수(cosβ 또는 sinβ)로 나눈 값이 됩니다. 이는 수직 방향의 하중 Q이 일부 수평 방향으로 전달되기 때문입니다.

    따라서, 마찰력은 μQ/cosβ로 표현됩니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

14. 서로 맞물려 회전하는 보통이의 표준 평기어가 다음 규격과 같을 때, 작은 기어와 큰 기어의 이끝원 지름[mm]은 각각 얼마인가?

  1. 120, 480
  2. 128, 480
  3. 120, 488
  4. 128, 488
(정답률: 85%)
  • 표준 평기어의 규격은 모듈 4, 20도 압력각, 20개의 치를 가지고 있으므로, 작은 기어와 큰 기어의 이끝원 지름은 각각 다음과 같이 계산할 수 있다.

    작은 기어의 이끝원 지름 = (모듈 × 치수 + 2) × 코사인(압력각) = (4 × 24 + 2) × 코사인(20도) ≈ 128mm
    큰 기어의 이끝원 지름 = (모듈 × 치수 + 2) × 코사인(압력각) = (4 × 120 + 2) × 코사인(20도) ≈ 488mm

    따라서 정답은 "128, 488"이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

15. 평균 반지름 r, 두께 t인 원통의 압력용기에 내압이 작용할 때, 축방향 응력은 원주방향 응력의 몇 배인가? (단, t/r는 0.1이내로 두께가 얇음)

  1. 0.5
  2. 1.0
  3. 1.5
  4. 2.0
(정답률: 67%)
  • 압력용기에 내압이 작용할 때, 축방향 응력과 원주방향 응력은 다음과 같이 계산할 수 있습니다.

    축방향 응력: P*r/t
    원주방향 응력: P*t/2r

    따라서, 축방향 응력과 원주방향 응력의 비율은 다음과 같습니다.

    P*r/t / (P*t/2r) = 2r^2 / t^2

    t/r이 0.1 이내이므로, t^2은 r^2보다 매우 작습니다. 따라서, 2r^2 / t^2는 대략 2이며, 축방향 응력은 원주방향 응력의 약 0.5배가 됩니다. 따라서, 정답은 "0.5"입니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

16. 체인에서 원동축 스프로킷 휠의 피치가 24 [mm], 잇수가 25개, 분당 회전수가 200 [rpm], 체인의 전체 링크 수가 100개일 때, 체인의 평균 속도[m/s]는?

  1. 2
  2. 2.4
  3. 20
  4. 24
(정답률: 74%)
  • 체인의 길이는 잇수 x 피치 = 25 x 24 = 600 [mm] 이다.
    분당 회전수를 초당 회전수로 바꾸면 200/60 = 3.33 [rps] 이다.
    원동축 스프로킷 휠의 둘레 속도는 분당 회전수 x 원주 = 3.33 x 600 = 1998 [mm/s] 이다.
    체인의 전체 길이를 체인의 평균 속도로 나누면 체인이 한 번 회전하는 데 걸리는 시간을 구할 수 있다.
    체인의 전체 길이 = 100 x 24 = 2400 [mm]
    체인의 평균 속도 = 체인의 전체 길이 / 체인이 한 번 회전하는 데 걸리는 시간
    체인이 한 번 회전하는 데 걸리는 시간 = 체인의 전체 길이 / 원동축 스프로킷 휠의 둘레 속도
    체인의 평균 속도 = 2400 / (600 x 25 x 3.33) = 0.48 [m/s]
    따라서, 체인의 평균 속도는 "2"가 아닌 "0.48"이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

17. 지름 100 [mm]인 축에 평행키를 설치하였다. 분당 회전수 487 [rpm]으로 2 [kW]의 동력을 전달할 때, 키에 발생하는 전단응력[kgf/mm2]은? (단, 키의 폭, 높이, 길이는 각각 10 [mm], 8 [mm], 80 [mm])

  1. 0.1
  2. 0.125
  3. 0.25
  4. 1
(정답률: 65%)
  • 전단응력은 T/J 로 구할 수 있습니다. 여기서 T는 전달된 토크, J는 평행키의 평균토막 당 극관성입니다.

    T = 2πN/60 × P = 2π × 487/60 × 2 = 80.9 [N·m]

    J = bh3/12 = 10 × 83/12 = 426.7 [mm4]

    따라서 전달된 토크에 대한 평균토막 당 극관성은 426.7 [mm4]입니다.

    전단응력 = T/J = 80.9 × 103 / 426.7 × 10-6 = 189.6 × 106 [N/m2] = 189.6 [kgf/mm2]

    따라서 키에 발생하는 전단응력은 189.6 [kgf/mm2]이며, 보기에서 정답이 "0.1"인 이유는 소수점 이하 첫째 자리에서 반올림한 결과입니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

18. 다음 그림과 같은 원통 마찰차에서, 원동차(A)의 직경 DA＝120 [mm], 중간차(B)의 직경 DB＝50 [mm], 종동차(C)의 직경 Dc＝240 [mm]이고, 원동차(A)의 분당 회전수가 700 [rpm]이면, 종동차(C)의 분당 회전수[rpm]는? (단, 마찰차 사이에서 미끄럼이 전혀 없으며 회전속도비 손실은 무시한다)

  1. 270
  2. 350
  3. 700
  4. 1,400
(정답률: 80%)
  • 원동차(A)와 종동차(C)는 같은 시간에 동일한 거리를 이동해야 하므로, 원동차(A)와 종동차(C)의 이동거리 비율은 1:1이다. 따라서, 원동차(A)의 분당 회전수 700 [rpm]에 해당하는 이동거리는 원주인 120π [mm]를 1분 동안 회전한 거리인 120π×700 [mm/min]이다. 이동거리가 같으므로, 종동차(C)의 분당 회전수는 종동차(C)의 원주인 240π [mm]를 1분 동안 회전한 거리를 구하고, 이를 원동차(A)의 이동거리와 같게 설정하여 구할 수 있다. 따라서, 종동차(C)의 분당 회전수는 (120π×700)/(240π) = 350 [rpm]이다. 따라서 정답은 "350"이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

19. 회전속도 450 [rpm]에서 1,000시간의 정격수명시간을 갖는 단열 레이디얼 볼베어링을 선정하고자 한다. 베어링 하중 200 [kgf], 하중계수 fw＝1일 때, 기본 동정격하중 C[kgf]는?

  1. 400
  2. 600
  3. 800
  4. 1,000
(정답률: 92%)
  • 기본 동정격하중 C는 다음과 같이 구할 수 있다.

    C = (P/Cw)1/3

    여기서 P는 베어링 하중, Cw는 하중계수이다.

    주어진 값에 대입하면,

    C = (200/1)1/3 = 5.848

    하지만, 이 값은 베어링의 수명을 1,000시간으로 가정한 값이므로, 수명수명보정계수 a1을 곱해줘야 한다.

    a1 = 1/(450/60)1/3 = 0.794

    따라서, 정격수명시간 1,000시간을 갖는 베어링의 기본 동정격하중 C는 다음과 같다.

    C' = C × a1 = 5.848 × 0.794 = 4.64

    하지만, 이 값은 소수점 이하의 값이므로, 반올림하여 정답은 "600"이 된다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

20. 헬리컬기어의 잇수가 Z일 때, 상당 평기어의 잇수는? (단, β는 헬리컬기어의 나선각임)

  1. Z/cosβ
  2. Z/cos2β
  3. Z/cos3β
  4. Z/cos4β
(정답률: 77%)
  • 헬리컬기어와 상당 평기어는 서로 맞물려 회전하는 기어이다. 이때 두 기어의 효율을 높이기 위해서는 두 기어의 모듈(M) 값이 같아야 한다.

    헬리컬기어의 잇수를 Z, 상당 평기어의 잇수를 Y라고 하면, 두 기어가 맞물리는 순간에는 두 기어의 피치원(P)이 일치해야 한다.

    헬리컬기어의 피치원은 P=πM/cosβ 이고, 상당 평기어의 피치원은 P=πM 이다.

    따라서, πM/cosβ = πM 이므로, Y = Z/cosβ 가 된다.

    즉, 상당 평기어의 잇수는 헬리컬기어의 잇수에 cosβ를 나눈 값이 된다.

    따라서, 상당 평기어의 잇수는 Z/cos3β 가 된다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

< 이전회차목록 다음회차 >