1. 유효깊이 d＝480mm, 압축연단에서 중립축까지의 거리 c＝160mm인 단철근 철근콘크리트 직사각형보의 휨파괴 시 인장철근 변형률은? (단, 인장철근은 1단 배근되어 있고, 파괴 시 압축연단 콘크리트의 변형률은 0.003이다)
- 0.003
- 0.004
- 0.005
- 0.006
2. 고장력 볼트이음에 대한 설명으로 옳지 않은 것은?
- 고장력 볼트는 너트회전법, 직접인장측정법, 토크관리법 등을 사용하여 규정된 설계볼트장력 이상으로 조여야 한다.
- 고장력 볼트로 연결된 인장부재의 순단면적은 볼트의 단면적을 포함한 전체 단면적으로 한다.
- 볼트의 최소 및 최대 중심간격, 연단거리 등은 리벳의 경우와 같다.
- 마찰접합은 고장력 볼트의 강력한 조임력으로 부재간에 발생하는 마찰력에 의해 응력을 전달하는 접합형식이다.
3. 단철근 철근콘크리트 직사각형보의 폭 b＝400mm, 유효깊이 d＝600mm이며, 전단철근 단면적 Av＝200mm2이고, 전단철근 간격 s＝300mm일 때, 보의 계수전단력 Vu[kN]는? (단,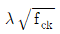 
＝5MPa, fyt=400MPa, 는 경량콘크리트 계수, fck는 콘크리트의 설계기준압축강도, fyt는 횡방향철근의 설계기준항복강도이다.)
- 270
- 360
- 420
- 540
4. 도로교설계기준(한계상태설계법, 2012)의 기반이 된 한계상태설계법에 대한 설명으로 옳지 않은 것은?
- 부분안전계수를 사용하여 하중 및 각 재료에 대한 특성이 고려된 설계법이다.
- 설계이론에서 재료는 선형탄성 구간에 있는 것으로 가정한다.
- 하중과 재료의 불확실성을 고려한 설계법으로 구조 신뢰성 이론에 기반하고 있다.
- 안정성과 사용성을 극한한계상태와 사용한계상태를 이용하여 확보한다.
5. 축력, 휨모멘트, 전단력의 작용에 의해 부재 단면에 발생하는 응력에 관한 설명으로 옳지 않은 것은?
- 인장력이 단면의 도심에 작용할 때, 하중작용점에서 충분히 멀리 떨어진 단면의 인장응력은 단면 내에 균등하게 분포된다.
- 휨모멘트가 작용할 때, 단면의 상하단 위치에서 최대압축 또는 최대인장 응력이 발생한다.
- 휨모멘트에 의한 휨응력은 단면의 단면2차모멘트가 클수록 작아진다.
- 전단력이 작용할 때, 직사각형 단면의 전단응력은 단면 내에 균등하게 분포된다.
6. 그림과 같이 설계 축력이 200kN인 고장력 볼트(F10T-M22 볼트) 5개를 이용하여 마찰이음 연결부를 설계할 때, 연결부의 공칭마찰강도[kN]는? (단, 도로교설계기준(한계상태설계법, 2012)에 따라 볼트의 공칭마찰강도는 Rn=KhKsNsPt로 계산하고, Kh는 구멍크기계수, Ks는 표면상태계수, Ns는 볼트 1개당 미끄러짐면의 수, Pt는 볼트의 설계 축력을 나타내며, Kh=0.4, Ks=0.6이다.)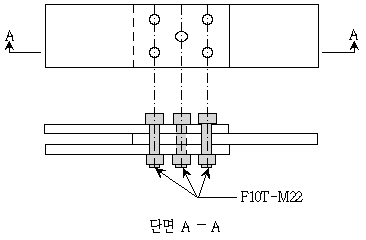
- 360
- 480
- 600
- 720
7. 양단이 고정되어 있는 길이 5m의 H형강(300×300×10×15)을 사용한 기둥의 오일러 좌굴하중[kN]은? (단, π2＝10으로 가정하고, H형강의 강축 및 약축의 단면2차모멘트 Ixx＝2×108mm4, Iyy＝5×107mm4, 탄성계수 E＝2.0×105MPa이다)
- 16,000
- 18,000
- 20,000
- 22,000
8. 그림과 같이 지간 L＝8m인 프리스트레스트 콘크리트 단순보의 지간 중앙에 집중하중 Q＝240kN이 작용하고 있다. 꺽인 직선 긴장재는 지간 중앙에 편심 e＝0.3m로 설치되었다. 하중평형법에 의해 집중하중 Q와 등가상향력의 크기가 같아지도록 하는 프리스트레스의 크기 P[kN]는? (단, sinθ=2e/L으로 가정하고, 프리스트레스의 손실은 무시하며, 집중하중은 자중을 포함하고 있다.)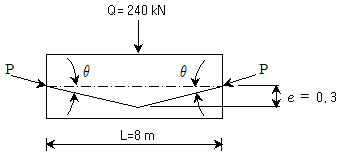
- 800
- 1,000
- 1,300
- 1,600
9. 다음의 철근콘크리트 확대기초에서 유효깊이 d＝550mm, 지압력 qu＝0.3MPa일 때, 1방향 전단에 대한 위험단면에 작용하는 전단력[kN]은?
- 420
- 520
- 620
- 720
10. 도로교설계기준(한계상태설계법, 2012)에 따른 신축이음 설계에 관한 설명으로 옳지 않은 것은?
- 신축이음의 설계 연직하중은 표준트럭의 후륜하중으로 한다.
- 신축이음의 설계 수평하중은 설계 연직하중의 20%로 하고 신축이음에서의 바퀴 접촉과 분포를 고려한다.
- 강교량인 경우 노면 틈새 간격은 계수하중을 고려한 극한 이동 상태에서 25mm 이상이어야 한다.
- 각종 이동량 및 시공 여유량 등을 모두 고려하여 차량 진행방향으로 산정한 신축이음 노면 최대 틈새 간격(W, mm)은 틈새가 하나(for single gap)인 경우 W ≤ 120mm를 만족하여야 한다.
11. 프리스트레스트 콘크리트 부재에서 프리스트레스의 감소 원인 중 프리스트레스 도입 후에 발생하는 시간적 손실의 원인에 해당하는 것은?
- 콘크리트의 크리프
- 정착장치의 활동
- 콘크리트의 탄성수축
- 긴장재와 덕트의 마찰
12. 단철근 철근콘크리트 직사각형보의 폭 b＝400mm, 유효깊이 d＝450mm이며, 인장철근 단면적 As＝1,700mm2, 콘크리트 설계기준압축강도 fck＝20MPa, 철근의 설계기준항복강도 fy＝400MPa일 때, 공칭휨강도 Mn[kNㆍm]은? (단, 인장철근은 1단 배근되어 있다)
- 192
- 232
- 272
- 312
13. 콘크리트 기초판에 수직력 P와 모멘트 M이 동시에 작용하고 있다. A지점에 압축응력이 발생하기 위한 최소 수직력 P[kN]는?
- 20
- 30
- 40
- 50
14. 콘크리트구조기준(2012)에 따라 철근콘크리트 휨부재의 모멘트 강도를 계산하기 위하여 사용하는 등가직사각형 응력블록에 대한 설명으로 옳지 않은 것은? (단, a는 등가직사각형 응력블록의 깊이, b는 단면의 폭, fck는 콘크리트의 설계기준압축강도이다)
- 콘크리트의 실제 압축응력분포의 면적과 등가직사각형 응력블록의 면적은 같다.
- 등가직사각형 응력블록의 도심과 실제 압축응력분포의 도심은 일치하지 않는다.
- 등가직사각형 응력블록에 의한 콘크리트가 받는 압축응력의 합력은 0.85fckab 계산한다.
- 등가직사각형 응력블록을 정의하는 주요 변수 값은 콘크리트 압축강도에 따라 달라진다.
15. 2방향 콘크리트 슬래브의 중앙에 집중하중 175kN이 작용할 때 장경간이 부담하는 하중[kN]은? (단, 장경간은 3m, 단경간은 2m이다)
- 40
- 50
- 60
- 70
16. 프리스트레스트 콘크리트의 성질에 관한 설명으로 옳지 않은 것은?
- 포스트텐션 방식에서 긴장재의 인장력은 긴장재 끝에서 멀어질수록 감소한다.
- 프리텐션 방식은 덕트를 통하여 배치한 긴장재를 콘크리트가 굳은 다음에 긴장시켜 프리스트레스를 주는 방식이다.
- 프리텐션 방식에서 프리스트레스를 도입하기 위하여 긴장재의 고정을 풀어주면 압축응력이 작용하여 콘크리트 부재는 단축되며, 긴장재의 인장응력은 감소한다.
- 긴장재와 덕트가 완전히 직선인 것으로 가정할 경우, 긴장재의 파상마찰로 인한 손실은 일어나지 않는다.
17. 철근 콘크리트의 전단설계에 관한 설명으로 옳은 것은? (단, s는 전단철근의 간격, Av는 전단철근의 단면적, fyt는 횡방향 철근의 설계기준항복강도, d는 유효깊이, α는 경사스터럽과 부재축 사이의 각도를 나타낸다)
- 계수전단력 Vu가 콘크리트가 부담하는 전단력 øVc보다 크지 않은 구간에서는 이론상 전단철근이 필요 없으므로, 실제 설계에서도 전단철근을 배근하지 않는다.
- 교대 벽체 및 날개벽, 옹벽의 벽체, 암거 등과 같이 휨이 주거동인 판부재에서는 최소 전단철근을 배근하지 않아도 된다.
- 경사스터럽을 전단철근으로 사용하는 경우에 스터럽이 부담하는 전단강도
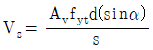이다. - 수직스터럽의 간격은 0.5d 이하, 800mm 이하로 하여야 한다.
18. 콘크리트구조기준(2012)에 따른 처짐을 계산하지 않는 경우의 철근콘크리트 1방향 슬래브의 최소 두께로 옳지 않은 것은? (단, 슬래브는 큰 처짐에 의해 손상되기 쉬운 칸막이벽이나 기타 구조물을 지지 또는 부착하지 않은 부재이고, 부재의 길이는 ℓ이다.)
- 1단 연속 1방향 슬래브 : ℓ/24
- 양단 연속 1방향 슬래브 : ℓ/28
- 단순지지 1방향 슬래브 : ℓ/16
- 캔틸레버 1방향 슬래브 : ℓ/10
19. 콘크리트구조기준(2012)에 따른 확대머리 이형철근의 인장에 대한 정착길이 계산식을 적용하기 위한 조건으로 옳지 않은 것은?
- 철근의 설계기준항복강도는 400MPa 이하이어야 한다.
- 콘크리트의 설계기준압축강도는 40MPa 이하이어야 한다.
- 철근의 지름은 40mm 이하이어야 한다.
- 확대머리의 순지압면적은 철근 1개 단면적의 4배 이상이어야 한다.
20. 다음 그림과 같은 박스형 단면을 갖는 철근콘크리트보의 공칭휨강도 Mn[kNㆍm]은? (단, fck＝20MPa, fy＝400MPa, fck는 콘크리트의 설계기준압축강도, fy는 철근의 설계기준항복강도이다.)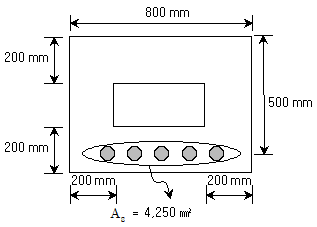
- 523.75
- 633.75
- 743.75
- 853.75
ε = (M * c) / (A * d^2 * f_y)
여기서 M은 균일하게 분포된 최대 굴곡모멘트, A는 인장철근의 단면적, f_y는 인장강도이다.
주어진 조건에서 균일하게 분포된 최대 굴곡모멘트는 M = (0.85 * f_c * b * d^2) / 2 이다. 여기서 f_c는 압축콘크리트의 고강도 경화제를 사용하지 않은 설계강도, b는 보의 폭이다.
따라서 M = (0.85 * 21 * 200 * 480^2) / 2 = 87,091,200 Nmm 이다.
인장철근의 단면적은 1단 배근되어 있으므로 A = (π * 12^2) / 4 = 113.1 mm^2 이다.
따라서 ε = (87,091,200 * 160) / (113.1 * 480^2 * 400) = 0.006 이다.
따라서 정답은 "0.006"이다.