1과목: 과목 구분 없음
1. 증류탑에서 원료 공급선(feed line)의 기울기가 영(0)인 원료 공급 조건에 해당하는 것은?
- 액체와 증기의 혼합 원료를 공급할 경우
- 포화증기를 공급할 경우
- 포화액체를 공급할 경우
- 과열 증기(superheated vapor)를 공급할 경우
2. 정상상태로 조업되는 반응기에 유입되는 흐름과 유출되는 흐름을 분석한 결과, 반응에 참여하지 않는 비활성물질의 조성이 유입 흐름과 유출 흐름에서 각각 20mol%와 10mol%이다. 이 반응기에 유입되는 흐름의 유속이 100mol/s일 때 유출 흐름의 유속[mol/s]은? (단, 반응기에서 반응물은 생성물로 100% 전환된다)
- 50
- 100
- 200
- 500
3. 유량의 조절 또는 개폐의 목적으로 사용되는 밸브의 종류와 이에 대한 설명으로 옳지 않은 것은?
- 게이트 밸브:유량 조절에 적합하며 압력 강하가 작다.
- 글로브 밸브:유량 조절에 널리 사용되며 압력 손실이 크다.
- 버터플라이 밸브:원판 회전에 의해 작동되며 개폐작용이 빠르고 간단하다.
- 체크 밸브:유체를 한쪽 방향으로만 흐르게 하여 역류를 방지한다.
4. 다음 분체 제조 장치 중, 가장 작은 크기의 분체를 제조할 수 있는 장치는?
- 콜로이드 밀(colloid mill)
- 선동 파쇄기(gyratory crusher)
- 중간형 해머 밀(intermediate hammer mill)
- jaw 파쇄기(jaw crusher)
5. 동점도(kinematic viscosity), 확산도(diffusivity) 및 열확산도(thermal diffusivity)의 차원은 모두 같다. 이들 차원으로 옳은 것은? (단, L은 길이, T는 시간, M은 무게를 나타낸다)
- L2 T-1
- M L2 T-1
- L-1 T2
- M L-1 T2
6. 증류탑의 총괄 단효율(overall tray efficiency)이 70%이고 McCabe-Thiele 법으로 구한 이론 단수가 20이라면 설계해야 할 증류탑의 실제 단수는? (단, 실제 단수는 소수점 첫째 자리에서 반올림한다)
- 6
- 14
- 20
- 29
7. 공기 100g의 온도를 20°C에서 50°C까지 승온하기 위해 필요한 열량[kcal]은? (단, 압력 변화는 없으며 공기의 정압비열(Cp)은 0.24kcal/kgㆍ°C이다)
- 0.24
- 0.56
- 0.72
- 1.20
8. 유체 속에서 중력 낙하하는 입자에 대한 설명으로 옳지 않은 것은?
- 입자에는 부력, 항력 및 중력이 작용하며 ‘가속력=중력-부력-항력’의 관계식이 성립한다.
- 입자가 가속됨에 따라 항력이 증가하면서 가속도를 감소시키며 결국 가속도가 영(0)이 될 때 종말 속도에 도달한다.
- 입자의 레이놀즈(Reynolds) 수가 1보다 상당히 작을 때(Re≪1) Stokes 법칙이 적용되며 이 때 항력계수(CD, drag coefficient)는 0.40~0.45로 거의 일정하다.
- 크기가 매우 큰 입자가 기체나 저점도 유체 내에서 낙하할 때에는 Stokes 법칙이 성립하지 않는다.
9. 성분 A, B로 구성된 이성분 혼합물이 x축 방향으로만 이동하고 있다. A, B 성분들의 밀도는 각각 ρA=1.5g/cm3, ρB=1.0g/cm3이며 속도는 각각 vA,x=2m/s, vB,x=-0.5m/s이다. Fick의 법칙에 의한 성분 A의 질량 플럭스[g/cm2ㆍs]는?
- 150
- 200
- 250
- 300
10. 온도가 같은 동일 부피의 수소 기체와 산소 기체의 무게를 측정하였더니 서로 동일하였다. 이때 수소 기체의 압력이 4atm이라면, 산소 기체의 압력[atm]은? (단, 수소 기체와 산소 기체는 이상기체로 가정한다)
- 1/4
- 1/2
- 1
- 2
11. 다음과 같은 복합 반응을 구성하는 반응 ㉠과 ㉡에서 반응물 A의 소멸속도를 각각 r㉠A, r㉡A라고 할 때, 반응물 B와 중간체 I에 대한 알짜 반응속도(net reaction rate) rB와 rI를 r㉠A와 r㉡A로 올바르게 나타낸 것은? (순서대로 rB, rI)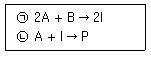
12. 내경이 10cm인 원형 관에 밀도가 1.5g/cm3인 유체가 2cm/s 속도로 흐르고 있다. 레이놀즈(Reynolds) 수가 60이라고 가정할 경우, 이 유체의 점도[g/cmㆍs]는?
- 0.2
- 0.3
- 0.4
- 0.5
13. 이상(ideal) 회분식 반응기에 대한 설명으로 옳지 않은 것은?
- 반응이 진행되는 동안 반응물과 생성물의 유입과 유출이 없다.
- 반응 시간에 따라 반응기 내의 조성이 변하지 않는 정상상태 조작이다.
- 조성과 온도는 반응기 내 위치와 무관하다.
- 전환율(conversion)은 반응물이 반응기 내에서 체류한 시간의 함수이다.
14. 지름이 5m인 물탱크에 5m의 높이로 물이 채워져 있다. 지름이 10cm인 수평관이 물탱크 바닥에 연결되어 있는 경우 배출구를 통한 초기 배출 속도[m/s]는? (단, 수평관에서의 마찰 손실은 무시하며 중력 가속도는 10m/s2로 가정한다)
- 5
- 10
- 15
- 20
15. 고체상의 수직벽에 의해 고온의 유체와 저온의 유체가 나뉘어져 있다. 두 유체 사이의 온도차가 2배로 증가된다면 이에 따른 열전달량은 몇 배인가? (단, 정상상태를 가정하며 총괄 열전달계수와 열전달 면적은 일정하다)
- 0.5
- 1.0
- 2.0
- 4.0
16. 다음은 흐름 단면이 원형인 관을 통해 흐르는 비압축성 유체의 속도 분포식이다. 이 유체의 평균 속도[m/s]는? (단, u는 유체의 속도, R은 관의 내반경, r은 관의 중심에서부터 반경 방향 거리이다)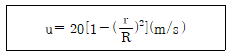
- 5
- 10
- 15
- 20
17. 내경이 2cm에서 4cm로 변하는 관에서 유체가 흐를 때 내경이 2cm인 관 내부에서 유체의 평균 유속이 1m/s라면, 내경이 4cm인 관 내부에서 유체의 평균 유속[m/s]은? (단, 유체의 밀도와 유량은 변화가 없으며 마찰은 무시한다)
- 4
- 2
- 0.5
- 0.25
18. 벽에 얇은 플라스틱판이 붙어 있다. 플라스틱판 양쪽의 온도는 각각 50°C와 55°C이다. 정상상태에서 벽으로 전달되는 열 플럭스(heat flux)[J/m2ㆍs]는? (단, 플라스틱판의 열전도도는 0.6J/mㆍsㆍ°C이다)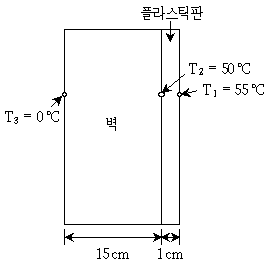
- 3
- 30
- 300
- 3,000
19. 총 외부 표면적이 100ft2인 향류(countercurrent)이중관 열교환기 내에서 유체 A가 질량 유속 10,000lb/h로 흐르며 200°F에서 100°F로 냉각된다. 냉각을 위해 50°F인 유체 B가 5,000lb/h의 유속으로 열교환기에 주입될 경우 대수평균온도차(log mean temperature difference)[°F]는? (단, 유체 A와 B의 열용량은 각각 0.5Btu/(lbㆍ°F), 0.8Btu/(lbㆍ°F)이며 ln2=0.7, 대수평균온도차 값은 소수점 첫째 자리에서 반올림한다)
- 36
- 48
- 60
- 72
20. 비압축성 뉴턴(Newtonian) 유체의 유동장을 나타내는 속도 벡터가 직교좌표계에서 다음과 같이 표현될 때, 비압축성을 항상 만족하기 위한 계수들(ai)의 관계식으로 옳은 것은? (단, 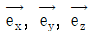 는 각각 x, y, z축의 단위 벡터이다)
는 각각 x, y, z축의 단위 벡터이다)
- a1+a2+a3+a4+a5+a6=1
- a1+a3+a5=0
- a2+a4+a6=1
- a1+a2=0






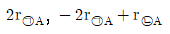
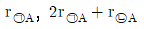
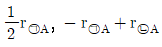
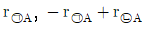
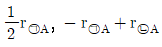 "이다.
"이다.