1과목: 과목 구분 없음
1. 다음 회로에서 출력전압 VXY는?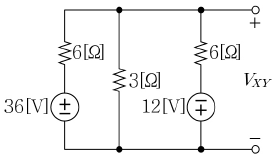
- 4[V]
- 6[V]
- 8[V]
- 10[V]
2. 10[H]의 유도용량을 가진 인덕터에 100[J]의 자기에너지를 저장하려면 전류를 얼마나 흐르게 해야 하는가?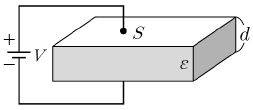
- √2[A]
- 1[A]
- 10[A]
- √20[A]
3. 다음 그림과 같이 면적 S[m2]와 간격 d[m]인 평행판 캐패시터가 전압 V[V]로 대전되어 있고, 유전체의 유전율이 ε[F/m]일 때, 축적된 정전에너지[J]를 구하면?
4. 액체 유전체를 포함한 콘덴서 용량이 C[F]인 것에 V[V]전압을 가했을 경우에 흐르는 누설전류는 몇 [A]인가? (단, 유전체의 유전율은 ε[F/m]이며, 고유저항은 ρ[Ωㆍm]라 한다.)
- CV / pε
- pεV / C
- pCV / ε
- CV2 / pε
5. 무한장 직선 도체에 전류 I[A]를 흘릴 때 이 전류로부터 d[m] 떨어진 점의 자속밀도는 몇 [Wb/m2]인가? (단, 이 도체는 공기 중에 놓여 있다.)
- μ0I / 2πd
- I / 2μ0d
- μ0I / 4πd
- μ0I / 4d
6. 도체에 정(+)의 전하를 주었을 때 다음 중 옳지 않은 것은?
- 도체 외측 측면에만 전하가 분포한다.
- 도체 표면에서 수직으로 전기력선이 발산한다.
- 도체 표면의 곡률 반지름이 작은 곳에 전하가 많이 모인다.
- 도체 내에 있는 공동면에도 전하가 분포한다.
7. 다음 그림의 회로에서 10[Ω]의 저항에 흐르는 전류의 값은?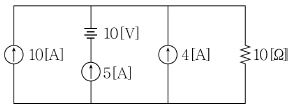
- 14[A]
- 19[A]
- 20[A]
- 24[A]
8. 다음 회로에서 t=0[s]일 때 스위치 S를 닫았다면, t=∞[s]에서 i1(t), i2(t)의 값은? (단, t<0[s]에서 C전압과 L전압은 0[V]이다.)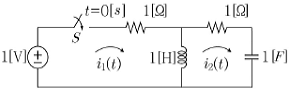
- i1(t)=-1[A], i2(t)=0[A]
- i1(t)=0[A], i2(t)=-1[A]
- i1(t)=1[A], i2(t)=0[A]
- i1(t)=0[A], i2(t)=1[A]
9. 다음 그림과 같은 평형 3상 회로로 운전되는 유도전동기(유도성부하)에서 전력계 W1, W2, 전압계 V, 전류계 A의 측정값이 각각 W1=3.4[kW], W2=1.7[kW], V=250[V], A=20[A]이였다면, 이 유도전동기의 역률 크기와 위상으로 각각 옳은 것은? (단, √3=1.7임)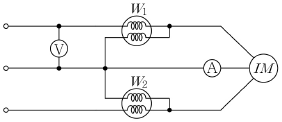
- 0.6, 지상
- 0.8, 지상
- 0.6, 진상
- 0.8, 진상
10. 전기장 내에서 +2[C]의 전하를 다른 점으로 옮기는 데 100[J]의 일이 필요했다면, 그 점의 전위는 ( ⓐ )[V] 높아진 상태이다. 다음 중 ⓐ의 값으로 옳은 것은?
- 2
- 20
- 40
- 50
11. R, L, C 직렬공진회로에서 전압 확대율(Q)의 표현으로 옳은 것은?
12. 어느 전기소자에 흐르는 전류가 i(t)=4t+2[A]일 때, t=1[s]와 t=3[s] 사이에 전기소자의 한 단자로 유입되는 전하량은 얼마인가?
- 10[C]
- 15[C]
- 20[C]
- 25[C]
13. 3[kW]의 전열기를 정격상태에서 2시간 사용하였을 때 열량[kcal]은?
- 3,882
- 4,276
- 4,664
- 5,184
14. 어떤 직렬 RC 저대역 통과 필터의 차단 주파수가 8[kHz]라고 한다. 이 저대역 통과 필터의 저항 값이 10[Ω]이라면, 이 저대역 통과 필터의 캐패시터 용량[μF]으로 가장 가까운 값은? (단, π=3.14임)
- 2
- 5
- 20
- 50
15. 다음 회로에서 ix를 구하면?
- 9[A]
- 1[A]
- 6[A]
- 2[A]
16. 다음 Laplace 변환에 대응되는 시간함수의 초기 값과 최종값은 얼마인가?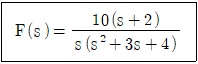
- f(0)=5, f(∞)=0
- f(0)=0, f(∞)=0
- f(0)=0, f(∞)=5
- f(0)=5, f(∞)=5
17. 다음 그림과 같은 회로에서 전류(I)[A]의 정상상태 값으로 옳은 것은?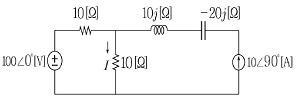
- 1+j
- 3+4j
- 4+3j
- 5+5j
18. 반경 1[mm], 길이 58[m]인 구리도선 양단에 직류 전압 100[V]가 인가되었다고 할 때, 이 구리도선에 흐르는 직류 전류[A]로 옳은 것은? (단, 이 구리도선은 균일한 단면을 가지는 단일 도체로 반경이 도선 전체에 걸쳐 일정하고, 이 구리도선의 도전율은 5.8×107[S/m]이라 가정하며, π=3.14임)
- 31.85
- 314
- 318.5
- 3140
19. 회로 (a)를 회로 (b)와 같이 등가회로로 변환할 때 VTh(단위[V])와 RTh(단위[Ω])의 합을 구하면?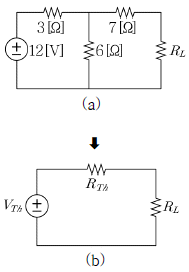
- 6
- 7
- 17
- 19
20. 다음 회로에서 부하저항 RL에 최대전력을 전달하기 위한 RS의 값은 얼마인가?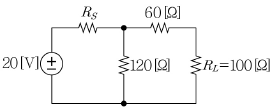
- 60[Ω]
- 80[Ω]
- 100[Ω]
- 120[Ω]






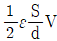
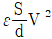
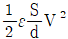
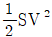
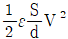 "입니다. 이유는 이 보기가 1/2 * (εS/d) * V2와 일치하기 때문입니다.
"입니다. 이유는 이 보기가 1/2 * (εS/d) * V2와 일치하기 때문입니다.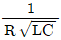
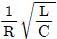
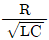
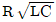
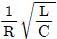 "입니다.
"입니다.
VX = 10V x (R2 / (R1 + R2)) = 10V x (2kΩ / (2kΩ + 1kΩ)) = 6.67V
VY = 4V x (R4 / (R3 + R4)) = 4V x (1kΩ / (1kΩ + 1kΩ)) = 2V
따라서, VXY = VX - VY = 6.67V - 2V = 4.67V ≈ 6V
따라서, 정답은 "6[V]" 입니다.