1과목: 과목 구분 없음
1. 두 평행판 사이에 공기가 채워져 있는 정전용량(Capacitance)이 1[μF]인 커패시터에 전극 간격의 1/3 두께를 가지는 유리판을 전극에 평행하게 넣는 경우 그 결과 얻어지는 정전용량은 얼마인가? (단, 유리의 비유전율은 2라고 가정한다.)
- 1[μF]
- 1.2[μF]
- 1.5[μF]
- 6[μF]
2. 다음에 주어진 회로의 부하에서 소비되는 전력이 최대가 되는 부하저항 RL[Ω]의 값으로 옳은 것은?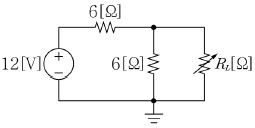
- 3[Ω]
- 6[Ω]
- 9[Ω]
- 12[Ω]
3. 다음 주어진 회로에서 각 저항에 흐르는 전류 I1[A], I2[A], I3[A] 값으로 옳은 것은?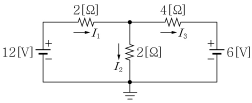
- I1=3[A], I2=3[A], I3=0[A]
- I1=3[A], I2=2[A], I3=1[A]
- I1=3[A], I2=1[A], I3=2[A]
- I1=3[A], I2=0[A], I3=3[A]
4. 아래 왼쪽 그림의 회로에 대하여 테브난(Thevenin)정리, 노턴(Norton)의 정리, 중첩의 원리를 이용하여 오른쪽 그림과 같은 테브난 등가회로를 구하고자 한다. v[V]와 R[Ω]의 값은 얼마인가?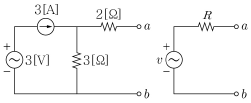
- v=6[V], R=3[Ω]
- v=9[V], R=3[Ω]
- v=6[V], R=5[Ω]
- v=9[V], R=5[Ω]
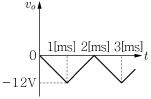
5. <보기>의 연산 증폭기 회로에서 구형파 전압(vi)이 인가될 때, 출력 전압(vo)의 파형을 옳게 그림으로 나타낸 것은? (단, 콘덴서의 초기전압은 0이며, 연산 증폭기는 이상적이고 입력신호의 동작주파수 범위에서 선형 동작을 한다고 가정한다.)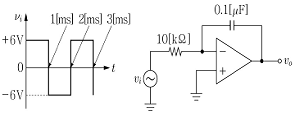
6. 다음의 BJT 증폭기 회로에 대한 설명 중 옳지 않은 것은?
- 에미터 저항 RE는 증폭기의 동작점을 안정화 한다.
- 바이패스 콘덴서 CE를 제거하면 증폭기의 전압이득이 증가한다.
- 바이패스 콘덴서 CE를 제거하면 증폭기의 입력 임피던스가 증가한다.
- 증폭기의 입력(vi)과 출력(vo)은 서로 역위상이다.
7. 다음 그림은 권선 수 비가 10:1(N1:N2)인 변압기 2차 측에 20[Ω]의 부하를 연결한 모습을 나타낸 것이다. 변압기 1차측에서 바라본 임피던스(Zi)로 옳은 것은? (단, 변압기는 이상적 변압기로 가정한다.)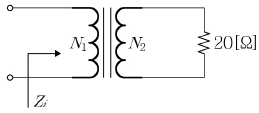
- 2[Ω]
- 20[Ω]
- 200[Ω]
- 2,000[Ω]
8. 다음과 같은 회로에서 에미터 전류 IE는? (단, 전류이득 β=100이고 실리콘 트랜지스터이며, VBE=0.7[V]이다.)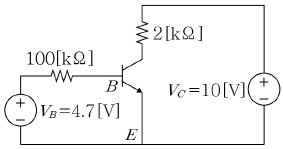
- 0.04[mA]
- 4.0[mA]
- 4.04[mA]
- 4.4[mA]
9. 다음의 독립 전압원과 독립 전류원으로 주어진 회로에서 2[Ω]의 저항에 흐르는 전류(I)는?
- 1.67[A]
- 2.50[A]
- 3.33[A]
- 5.00[A]
10. 접합 트랜지스터에서 α와 β의 관계는? (단, 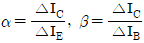 )
)
- β=(1-α)/α
- β=α/(1-α)
- β=(1+α)/α
- β=α/(1+α)
11. PN접합에서 순방향으로 전압을 걸어줄 때 나타나는 현상으로 옳은 것은?
- 다수의 캐리어가 서로 다른 쪽에 주입된다.
- P형 쪽의 전자만이 N형 쪽으로 주입된다.
- P형 쪽의 정공만이 N형 쪽으로 주입된다.
- 전류가 거의 흐르지 않는다.
12. 다음 회로에서 v1=2[V], v2=1[V]일 때, 출력단의 전압 vo[V]는?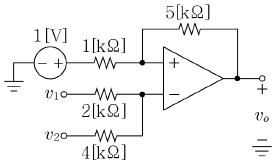
- 3[V]
- 4[V]
- 5[V]
- 6[V]
13. R1=R2=1[kΩ], R3=R4=2[kΩ]일 때, 아래 회로의 관계식은?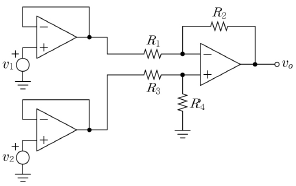
- Vo=V1-2V2
- Vo=V2-V1
- Vo=2V2-V1
- Vo=2(V2-V1)
14. 이상적인 연산증폭기의 특성이 아닌 것은?
- 전압 이득이 무한대
- 대역폭이 무한대
- 출력저항이 무한대
- 오프셋이 0
15. <보기>의 부울 함수를 간소화한 결과로 옳은 것은?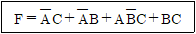

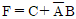
- F=C+B
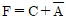
16. 한 변의 길이가 a[m]인 정사각형의 꼭짓점에 다음과 같이 +Q[C] 또는 +2Q[C]의 전하량을 가지는 전하를 놓을 때 정사각형의 중심에서의 전계[V/m]의 세기는?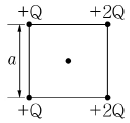
- 0
- Q/(4πε0a2)
- Q/(2πε0a2)
- Q/(√2πε0a2)
17. 다음의 회로가 XNOR(exclusive NOR)로 동작하기 위해 ㉠ 안에 하나의 논리 게이트(logic gate)소자만 들어갈 경우, 해당 논리 게이트 소자로 옳은 것은?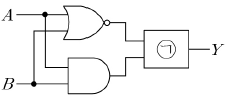
- AND
- NAND
- OR
- NOR
18. 다음 논리회로에서 A=0, B=1, C=1, D=0일 때, 출력 X, Y의 논리 상태로 옳은 것은?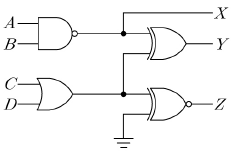
- X=1, Y=0, Z=0
- X=0, Y=1, Z=0
- X=0, Y=0, Z=1
- X=1, Y=1, Z=0
19. 그림과 같은 교류 브리지(bridge)의 평형조건은?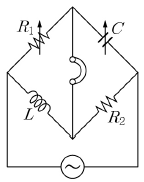
- R2/R1 = L/C
- R1L = R2/C
- R1C= L/R2
- R1R2 = CL
20. 다음 회로에서 교류 전압원 vs(t)=1000sin(1000t)[V]가 인가될 때 흐르는 전류 i(t)를 구한 것으로 옳은 것은?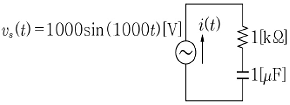
- √2sin(1000t-45°)[A]
- (1000/√2)sin(1000t+45°)[A]
- (1000/√2)sin(1000t-45°)[A]
- (1/√2)sin(1000t+45°)[A]






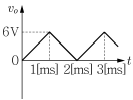
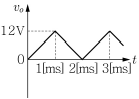
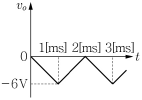
 "가 정답이 된다.
"가 정답이 된다.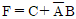 "가 옳다.
"가 옳다.
유리판을 넣으면, 유리의 비유전율이 2이므로, 유리판의 두께는 d/3이 된다. 이 때, 유리판을 넣기 전과 같은 전압 V를 가하면, 유리판을 넣기 전과 같은 전하 Q가 유리판을 통과하므로, 유리판에 저장된 전하는 Q/2가 된다. 따라서, 유리판을 넣은 후의 전극 간격은 2d/3이 되고, 전극의 면적은 변하지 않으므로, 유리판을 넣은 후의 정전용량은 C' = εA/(2d/3)가 된다.
이를 C로 나타내면, C' = (2/3)C이다. 따라서, 유리판을 넣은 후의 정전용량은 원래의 정전용량의 2/3이 된다. 따라서, C' = (2/3) × 1[μF] = 0.67[μF]이다. 하지만, 보기에서는 1.2[μF]가 정답이므로, 이는 유리판을 넣은 후의 정전용량이 아니라, 유리판을 넣기 전의 정전용량과 유리판을 넣은 후의 정전용량을 직렬로 연결한 경우의 정전용량이다. 이 경우, 두 커패시터의 정전용량을 더하면 된다. 따라서, 전체 정전용량은 1[μF] + 0.67[μF] = 1.67[μF]가 된다. 하지만, 보기에서는 1.2[μF]가 정답이므로, 이는 계산상의 실수일 가능성이 있다.