1과목: 과목 구분 없음
1. 2단의 단이 진축의 직경이 d와 D(>d)이고, 연결부의 필렛 반경은 r이다. 축의 피로수명을 증가시킬 수 있는 조합은?
- r의 증가, D/d 비의 증가
- r의 감소, D/d 비의 증가
- r의 증가, D/d 비의 감소
- r의 감소, D/d 비의 감소
2. 브레이크 드럼의 지름이 200mm, 브레이크에 작용하는 반경방향 수직력이 100 N일 때 브레이크 드럼에 작용하는 제동 토크 [N·mm]는? (단, 마찰계수 μ=0.3으로 한다)
- 2000
- 3000
- 4500
- 6000
3. 축(shaft)을 설계할 때 고려할 사항으로 옳지 않은 것은
- 전동축의 경우는 굽힘응력과 비틀림에 의한 전단응력이 같이 발생한다.
- 동일 재료의 경우 중공축은 동일 단면적을 갖는 중실축에 비해 전달할 수 있는 토크가 작다.
- 축이 베어링으로 고정되었을 때는 축변형의 경사각도 고려하여 설계하여야 한다.
- 기어 또는 벨트 풀리를 고정하여 사용하는 전동축은 상당굽힘 모멘트와 상당비틀림모멘트를 이용하여 안전 여부를 판단한다.
4. 다음 중 나사에 대해 설명한 것으로 옳지 않은 것은?
- M4 × 0.5는 호칭지름이 4 mm이고, 피치가 0.5 mm인 미터가는나사이다.
- 나사를 1회전 했을 때에 축 방향으로 이동하는 거리를 리드(lead)라고 한다.
- 암나사의 호칭지름은 결합되는 수나사의 바깥지름으로 나타낸다.
- UNC
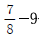 는 유니파이 보통나사이며, 피치는 9 mm이다.
는 유니파이 보통나사이며, 피치는 9 mm이다.
5. 고정되어 있지 않은 관에 온도변화가 있을 때 신축량에 대한 설명 중에서 옳은 것은?
- 신축량은 관의 열팽창계수에 비례하고 길이와 온도변화에 반비례한다.
- 신축량은 관의 열팽창계수, 길이, 온도변화에 반비례한다.
- 신축량은 관의 길이와 온도변화에 비례하고 열팽창계수에 반비례한다.
- 신축량은 관의 열팽창계수, 길이, 온도변화에 비례한다.
6. 중심거리가 70mm이고, 피니언 잇수가 24, 기어 잇수가 46인 표준 스퍼기어가 맞물려 있다. 잇수 46인 기어의 이끝원 지름[mm]은?
- 45
- 48
- 92
- 96
7. 볼트의 항복응력은 100MPa이다. 이 볼트에 허용 설계하중이 작용할 때, 축방향의 인장응력 30MPa과 비틀림에 의한 전단응력 20 MPa이 동시에 발생되었다. 최대주응력설을 적용하여 항복응력에 대한 안전계수를 구하면?
- 2.5
- 3.0
- 3.5
- 4.0
8. 두께가 같은 두 판재를 맞대기 용접하였을 경우 인장하중 P=48kN에 대한 인장응력이 6MPa이었을 때 이 판재의 두께[cm]는? (단, 용접길이(L)은 32 cm이다)
- 15
- 25
- 1.5
- 2.5
9. 용접이음으로 만든 지름이 1m인 구형 탱크(ball tank)에 내압이 4.5MPa이 되도록 가스를 주입하려고 한다. 허용인장응력이 100MPa이면 두께[mm]를 최소한 얼마로 하면 적당한가? (단, 이음 효율은 90%이고 부식여유 C는 1 mm로 한다)
- 12.3
- 13.5
- 26.0
- 51.0
10. 다음과 같은 판스프링에 하중 P가 작용할 때 처짐량은 1이다. 단면의 높이 h가 두 배가 되었을 때 스프링 상수는 얼마가 되겠는가?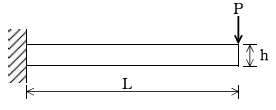
- 1/8P
- 8P
- 1/2P
- 2P
11. 두 줄 나사에서 피치 p, 유효지름 d, 나선각(리드각)을 α라 하면 tanα의 값은?
12. 두 판재가 양쪽 덮개판 한 줄 맞대기 이음으로 리벳 결합되어 있다. 리벳 한 개에 작용하는 전단하중을 W, 리벳의 지름을 d라고 할 때, 설계 시 리벳에 작용하는 전단응력 중 가장 적당한 것은?
13. 잇수가 동일한 4개의 평기어(spur gear)가 있다. 이들의 이의 크기는 다음과 같다. 다음 중 지름이 가장 큰 기어는? (단, m은 모듈, pd는 지름피치이다)
- m=5
- pd=4
- m=6
- pd=7
14. 하중 P에서 수명이 L인 볼 베어링에 두 배의 하중 2P가 작용할 때 수명은?
15. 다음에 제시한 축이음 방법 중에서 두 축 간의 축경사나 편심을 흡수할 수 없는 축이음 방법은?
- 고무 커플링
- 기어 커플링
- 유니버셜 조인트
- 플랜지 커플링
16. 잇수가 30인 스프로킷 휠이 500 rpm으로 회전하고 있다. 체인의 피치가 25mm일 때 체인의 평균속도[m/s]는?
- 6.25
- 6.35
- 6.45
- 6.55
17. 외접하는 원추 마찰차에서 원동차의 원추각은 30°, 종동차의 원추각은 60°이다(원추각은 꼭지각의 절반에 해당하는 각이다). 원동차에 대한 종동차의 회전속도비는?
- sin60°/sin30°
- tan30°
- cos60°
- sin60°
18. 6m/s의 속도로 6 kW를 전달하는 벨트 전동장치에서 긴장측의 장력이 2000N일 때 이완측에 대한 긴장측의 장력비는?
- 1.5
- 1.6
- 1.8
- 2.0
19. 직경 d를 갖는 중실축에 비해 동일 재질의 직경 d/2인 중실축이 전달할 수 있는 토크비 (Td/2/Td는?
- 1/2
- 1/4
- 1/8
- 1/16
20. 묻힘키가 받을 수 있는 토크와 축이 받을 수 있는 토크가 같다면, 축과 보스 경계면에서 키가 전단되는 경우 축지름 d, 키의 유효 길이 l, 폭 b사이의 관계식은? (단, 축과 키 재료는 동일하다)






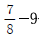 는 유니파이 보통나사이며, 피치는 9 mm이다. 이 설명이 옳지 않습니다. UNC는 미국 표준 나사이며, 피치는 인치당 나사 간격을 나타내는 단위인 TPI (Threads Per Inch)로 표시됩니다. 따라서 UNC의 피치는 9mm가 아니라 TPI로 표시됩니다.
는 유니파이 보통나사이며, 피치는 9 mm이다. 이 설명이 옳지 않습니다. UNC는 미국 표준 나사이며, 피치는 인치당 나사 간격을 나타내는 단위인 TPI (Threads Per Inch)로 표시됩니다. 따라서 UNC의 피치는 9mm가 아니라 TPI로 표시됩니다.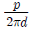

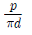
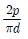
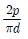 "가 정답입니다.
"가 정답입니다.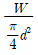
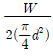
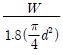
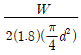
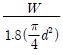 "이 가장 적당한 선택입니다. 이유는 리벳의 지름이 크면 단면적이 커져서 전단응력이 작아지기 때문입니다.
"이 가장 적당한 선택입니다. 이유는 리벳의 지름이 크면 단면적이 커져서 전단응력이 작아지기 때문입니다.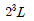
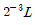
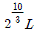
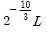
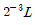 "입니다.
"입니다.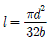
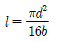
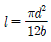
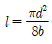
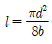 " 입니다.
" 입니다.