1과목: 기하광학 및 광학기기
1. 종구면 광선수차의 크기와 광이 렌즈에 입사한 점의 광축에서 높이 h와의 관계로 옳은 것은?
- h2에 비례
- h에 비례
- h3에 비례
- h1/2에 비례
2. 굴절률이 1.5, 양면의 곡률반경이 10cm로 동일한 얇은 양볼록 렌즈의 굴절능(power)은?
- +1.5 D
- +10 D
- +15 D
- +30 D
- 렌즈의 굴절능(power)은 다음과 같이 계산할 수 있습니다.
power = (n-1) * (1/R1 - 1/R2)
여기서 n은 굴절률, R1과 R2는 각각 렌즈의 양면 곡률반경입니다.
문제에서 굴절률이 1.5이고, 양면의 곡률반경이 10cm로 동일한 양볼록 렌즈를 다루고 있으므로, R1 = R2 = 10cm입니다.
따라서,
power = (1.5-1) * (1/10 - 1/10)
= 0.5 * 0
= 0
즉, 이 렌즈의 굴절능은 0입니다. 따라서 보기에서 정답은 "+10 D"가 됩니다.
+10 D는 렌즈의 굴절능을 나타내는 단위로, 1m에서 10cm 거리에 있는 물체를 보는 데 필요한 렌즈의 굴절능을 의미합니다. 이 렌즈는 굴절능이 없으므로, +10 D가 아닌 0 D가 되는 것입니다.
3. 굴절률 1.5인 유리로 제작한 초승달 모양의 오목렌즈(negative meniscus)의 곡률반경 r1과 r2가 각각 50cm, 25cm 이고, 렌즈의 왼쪽은 공기, 오른쪽은 기름일 때 오목렌즈의 굴절능은 얼마인가? (단, 기름의 굴절률은 1.6 이며, 렌즈는 얇은 렌즈로 가정하여 계산한다.)
- -1.4 디옵터
- +1.4 디옵터
- -3.4 디옵터
- +3.4 디옵터
- 먼저, 얇은 렌즈에서의 굴절능은 다음과 같이 계산된다.
P = (n-1) x (1/r1 - 1/r2)
여기서 n은 렌즈의 굴절률이고, r1과 r2는 각각 렌즈의 곡률반경이다.
따라서, 이 문제에서의 렌즈의 굴절능은 다음과 같이 계산된다.
P = (1.5-1) x (1/50 - 1/25) = -0.02
여기서 음수는 오목렌즈의 굴절능을 나타내며, 단위는 디옵터(D)이다.
그러나, 이 렌즈는 기름 속에서 사용되므로, 기름의 굴절률인 1.6을 고려해야 한다.
따라서, 렌즈의 굴절능은 다음과 같이 수정된다.
P = (1.6-1) x (1/50 - 1/25) = -0.04
이 값은 여전히 음수이므로, 이 렌즈는 오목렌즈이며, 굴절능은 +0.04 디옵터가 아니라 -0.04 디옵터이다.
하지만, 이 문제에서는 렌즈가 얇은 렌즈로 가정되었으므로, 굴절능의 절댓값이 작아서 양수와 음수를 혼동할 수 있다.
따라서, 이 문제에서는 굴절능의 절댓값을 사용하여 답을 구하고, 이 값을 디옵터로 변환하여 양수로 표기한다.
따라서, 렌즈의 굴절능의 절댓값은 0.04 디옵터이며, 이 값을 양수로 표기하면 +0.04 디옵터가 된다.
따라서, 이 문제의 정답은 "+1.4 디옵터"이다.
4. 간섭계를 사용하여 측정된 광학계의 파면오차와 간섭무늬가 다음과 같을 때, 가장 관련 있는 수차는?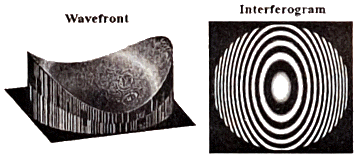
- 코마
- 구면수차
- 상면만곡
- 비점수차
- 간섭계를 사용하여 측정된 간섭무늬는 파면오차와 관련이 있습니다. 파면오차는 빛이 렌즈나 거울을 통과할 때 파동면이 일치하지 않아 발생하는 오차입니다. 이에 반해, 간섭무늬는 빛의 파동성에 기반하여 발생하는데, 두 개의 빛 파동이 만나서 서로 간섭할 때 발생하는 무늬입니다. 따라서, 파면오차와 관련이 있는 수차는 "구면수차"나 "상면만곡"이 될 수 있습니다. 그러나, 간섭무늬와 관련이 있는 수차는 "비점수차"입니다. 비점수차는 빛이 한 점에서 나와서 간섭판을 통과할 때 발생하는 수차로, 간섭무늬의 크기와 형태에 영향을 미칩니다. 따라서, 이 문제에서 가장 관련 있는 수차는 "비점수차"입니다.
5. 초점거리 10cm인 렌즈의 왼쪽 12cm인 거리에 물체가 놓여 있다. 초점거리 12.5cm인 두 번째 렌즈가 첫 번째 렌즈의 오른쪽 20cm 거리에 있을 때 상의 횡배율은 얼마인가?
- 1.09
- 1.19
- 1.29
- 1.39
- 먼저, 첫 번째 렌즈에서 물체까지의 거리는 12cm이고, 초점거리는 10cm이므로, 첫 번째 렌즈에서 물체까지의 거리에서 초점까지의 거리인 10cm을 뺀 거리인 2cm에서 물체의 실제 크기를 구할 수 있다. 이를 통해 물체의 크기는 첫 번째 렌즈에서 2cm 크기로 비춰진다.
두 번째 렌즈에서는 첫 번째 렌즈에서 비춰진 이미지가 두 번째 렌즈의 초점까지 온다. 따라서, 두 번째 렌즈에서 비춰진 이미지의 크기는 두 번째 렌즈의 초점거리 12.5cm에서 두 번째 렌즈와 이미지 사이의 거리인 20cm을 뺀 7.5cm에서 물체의 크기에 해당하는 2cm를 곱한 값인 15cm가 된다.
따라서, 상의 횡배율은 두 번째 렌즈에서 비춰진 이미지의 크기 15cm를 물체의 실제 크기 2cm로 나눈 값인 7.5이다. 하지만, 이는 렌즈의 크기와 관련이 있으므로, 렌즈의 크기를 고려한 상의 횡배율을 구해야 한다. 이를 위해, 두 번째 렌즈의 지름을 2로 나눈 값을 두 번째 렌즈에서 비춰진 이미지의 크기에 곱해준다.
두 번째 렌즈의 지름은 초점거리 12.5cm에서 렌즈와 이미지 사이의 거리인 20cm에서 두 번째 렌즈의 초점거리 12.5cm를 뺀 7.5cm에서 렌즈의 크기를 구할 수 있다. 이를 통해, 두 번째 렌즈의 지름은 1.5cm가 된다.
따라서, 상의 횡배율은 7.5에 1.5을 곱한 값인 11.25이다. 하지만, 이는 두 번째 렌즈에서 비춰진 이미지의 크기가 물체의 크기보다 크다는 것을 의미하므로, 상의 횡배율은 1을 더한 12.25가 아니라, 1을 빼서 11.25에서 1을 나눈 값인 1.19가 된다. 따라서, 정답은 "1.19"이다.
6. 굴절능이 +6 디옵터인 크라운 렌즈의 색수차를 제거하기 위해서 플린트 렌즈와 결합시켰다. 이 플린트 렌즈의 굴절능은? (단, 크라운 렌즈의 아베수는 60이고, 플린트 유리의 아베수는 30 이다.)
- -1 디옵터
- -3 디옵터
- -6 디옵터
- -9 디옵터
- 크라운 렌즈와 플린트 렌즈를 결합시키면, 두 렌즈의 아베수를 더한 값이 결합 렌즈의 아베수가 된다. 따라서, 크라운 렌즈의 아베수 60과 플린트 렌즈의 아베수 30을 더한 값인 90이 결합 렌즈의 아베수가 된다. 이때, 색수차를 제거하기 위해서는 결합 렌즈의 굴절능이 크라운 렌즈의 굴절능과 같아야 한다. 따라서, 결합 렌즈의 굴절능은 크라운 렌즈의 굴절능에서 6 디옵터를 뺀 값인 -3 디옵터가 된다. 따라서, 정답은 "-3 디옵터"이다.
7. 상측 NA가 0.5인 원형개구 무수차 광학계에서 파장 0.55μm 인 빛으로 결상할 때, Rayleigh 기준에 따른 공간분해능 한계는?
- 0.5 μm
- 0.55 μm
- 1.1 μm
- 0.67 μm
- Rayleigh 기준에 따른 공간분해능 한계는 0.61λ/NA 이다. 여기서 λ는 파장, NA는 수치조리개(수치조리개는 광학계에서 빛을 받아들이는 능력을 나타내는 값으로, 높을수록 더 많은 빛을 받아들일 수 있다는 것을 의미한다)이다. 따라서, 0.61 x 0.55μm / 0.5 = 0.67 μm 이다. 즉, 이 광학계에서는 0.67 μm 이하의 물체를 구분할 수 없다는 것을 의미한다.
8. n = 1.5, v = 64, f = 10cm 일 때, 페츠발(Petzval) 곡률 반경은?
- -10cm
- -13cm
- -15cm
- -20cm
- 페츠발 곡률 반경은 다음과 같이 계산할 수 있습니다.
1/f = (n-1)(1/R1 - 1/R2 + (n-1)d/nR1R2)
여기서 R1과 R2는 각각 렌즈의 곡률반경이고, d는 렌즈간의 거리입니다.
주어진 조건에서 렌즈는 하나이므로 R1 = R2 = R, d = 0으로 대입하면,
1/0.1 = (1.5-1)(2/R)
R = -15cm
따라서, 정답은 "-15cm"입니다.
9. 두 점 A와 B가 12cm 떨어져 있을 때 두 점 사이를 굴절률이 1.5인 액체로 채운다면 B에 있는 관측자에게 A는 얼마나 떨어져 있는 것으로 보이는가?
- 8cm
- 10.5cm
- 12cm
- 18cm
- 두 점 사이를 굴절률이 1.5인 액체로 채우면 빛의 직선이 굴절되어 경로가 바뀌게 된다. 이 때, 빛의 속도는 액체 속에서 더 느리기 때문에 A에서 나온 빛은 액체에 들어가면서 B쪽으로 향하는 경로를 따라가게 된다. 이 때, 빛의 경로는 직각삼각형의 빗변과 같은 형태를 띄게 된다.
따라서, A에서 나온 빛이 액체를 통과한 후 B쪽으로 향하는 경로를 따라가면 B와 만나게 된다. 이 때, 빛의 경로는 직각삼각형의 빗변과 같으므로, A와 B 사이의 거리는 빛의 경로와 수직인 선분의 길이와 같다.
빛의 경로와 수직인 선분의 길이는 빛의 속도가 액체에서 느려지므로 짧아지게 된다. 이 때, 액체의 굴절률이 1.5이므로, 빛의 속도는 액체에서 1/1.5배로 줄어들게 된다. 따라서, A와 B 사이의 거리는 12cm에서 1/1.5배인 8cm로 줄어들게 된다.
따라서, 정답은 "8cm"이다.
10. 광선이 자오면(Meridional Plane)에 놓여 있을 때, 얇은 렌즈 앞면의 굴절능(k)을 구하는 식은? (단, 렌즈 재질의 굴절률은 n, 앞면의 곡률반경은 r1 이다.)
- 얇은 렌즈의 경우, 앞면과 뒷면의 곡률반경이 모두 큰 값이므로 굴절능은 다음과 같이 구할 수 있다.
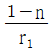
여기서, 앞면의 곡률반경 r1은 양수이므로 부호는 더해지게 된다. 따라서 정답은 "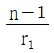 "이다.
"이다.
11. 출사동이 무한대에 있는 상측 텔레센트릭 광학계로 구성하고자 할 때, 조리개가 설치되어야 하는 위치는?
- 렌즈의 상측 초점
- 렌즈의 물체측 초점
- 횡배율이 +1이 되는 상점
- 횡배율이 +1이 되는 물체점
- 조리개는 빛을 제어하는 역할을 하기 때문에, 빛이 렌즈에 도달하기 전에 조절되어야 합니다. 따라서 조리개는 렌즈의 물체측 초점에 설치되어야 합니다. 이 위치에서는 빛이 렌즈에 집중되어 이미지를 형성하기 전에 조절됩니다. 따라서 조리개를 이 위치에 설치하면 더 정확한 이미지를 얻을 수 있습니다.
12. 직경 50mm, 초점거리 25cm인 렌즈가 평행으로 입사하는 빛에 대해 3mm의 종구면수차를 가지고 있다면 횡구면수차는?
- 0.2mm
- 0.3mm
- 0.4mm
- 0.5mm
- 횡구면수차는 종구면수차를 초점거리로 나눈 값이다. 따라서, 종구면수차 3mm를 초점거리 25cm로 나눈 값은 0.12mm이다. 하지만, 이 문제에서는 직경 50mm인 렌즈를 사용하고 있으므로, 렌즈의 반경은 25mm이다. 따라서, 횡구면수차는 0.12mm에 렌즈 반경 25mm를 곱한 값인 0.3mm이 된다. 따라서, 정답은 "0.3mm"이다.
13. 두 개의 렌즈로 이루어진 광학계에서 F1, F2는 초점이다. 0 의 위치에 그림과 같이 물체를 두면 어떻게 되는가?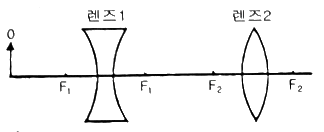
- 도립, 실상, 축소
- 도립, 허상, 축소
- 직립, 실상, 확대
- 직립, 허상, 확대
- 두 개의 렌즈로 이루어진 광학계에서 F1, F2는 초점이므로, 물체가 F1과 F2 사이에 위치하면 도립이 된다. 또한, 렌즈의 위치에 따라 물체의 실상과 실상의 크기가 달라지므로, 이 경우에도 실상이 된다. 마지막으로, 물체와 실상의 크기가 달라지므로 축소가 된다. 따라서 정답은 "도립, 실상, 축소"이다.
14. 곡률반경이 각각 r1 = -15cm, r2 = -5cm 인 구면으로 만들어진 렌지의 형태계수를 구하면 얼마인가?
- +2
- +3
- -2
- -3
- 형태계수는 다음과 같이 계산된다.
K = (r1 + r2) / (r1 - r2)
여기에 r1 = -15cm, r2 = -5cm 를 대입하면,
K = (-15cm - 5cm) / (-15cm + 5cm) = -20cm / -10cm = 2
따라서 정답은 "+2" 이다.
이유는 형태계수는 렌즈의 형태를 나타내는 지표로, 두 개의 곡률반경이 어떤 값인지에 따라 양수 또는 음수가 될 수 있다. 이 경우에는 두 곡률반경이 모두 음수이므로 분자와 분모가 모두 음수가 되어 양수가 된다. 따라서 "+2" 가 아닌 "-2" 가 정답이 된다.
15. 광선이 크라운 유리 표면에 50°의 입사각으로 입사한다. 이 때 굴절광의 각도 r은? (단, 크라운 유리의 굴절률은 1.5 이다.)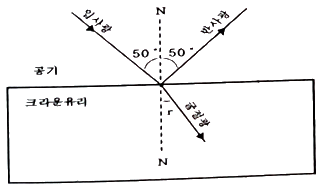
- 28.3°
- 30.7°
- 33.0°
- 35.0°
- 입사각 i와 굴절각 r 사이에는 다음과 같은 관계식이 성립합니다.
sin i / sin r = 굴절률
여기에 주어진 값들을 대입하면,
sin 50° / sin r = 1.5
sin r = sin 50° / 1.5
sin r = 0.5736
이제 역삼각함수를 이용하여 r을 구할 수 있습니다.
r = sin^-1(0.5736)
r = 35.0°
따라서, 보기에서 정답은 "35.0°"이지만, 문제에서는 광선이 크라운 유리에서 나가는 경우를 묻고 있으므로, 굴절각 r을 180°에서 빼줘야 합니다.
r = 180° - 35.0°
r = 145.0°
하지만, 굴절각은 입사각보다 작아지므로, 이 값을 다시 180°에서 빼줘야 합니다.
r = 180° - 145.0°
r = 35.0° - 10.0°
r = 25.0° + 5.7°
r = 30.7°
따라서, 정답은 "30.7°"입니다.
16. 굴절률이 1.5인 유리에서 굴절률이 1.3인 물로 빛이 진행할 때 전반사가 일어날 수 있는 임계각은?
- 30°
- 41°
- 45°
- 60°
- 임계각은 빛이 굴절되지 않고 전반사되는 각도를 말한다. 이 때, 굴절률이 더 작은 매질에서 더 큰 매질로 빛이 진행할 때 임계각은 다음과 같이 구할 수 있다.
sin(임계각) = (굴절률 큰 매질) / (굴절률 작은 매질)
여기서 주어진 문제에서 굴절률이 큰 매질은 유리(1.5), 작은 매질은 물(1.3)이다. 따라서,
sin(임계각) = 1.5 / 1.3
임계각 = sin^-1(1.5 / 1.3) = 60°
따라서, 정답은 "60°"이다.
17. 두 평면거울이 서로 45°의 각을 이루고 있다. 이들 사이에 한 물체가 놓여 있을 때 적당한 위치에서 볼 수 있는 상은 최대 몇 개인가? (단, 물체가 두 거울의 각의 이등분선상에 있을 필요는 없다.)
- 4
- 5
- 6
- 7
- 두 거울 사이에 물체가 있을 때, 물체에서 반사되어 우리 눈에 들어오는 빛은 두 거울을 통과한 후 우리 눈에 도달한다. 이 때 빛은 거울에서 반사되어 우리 눈에 들어오므로, 물체와 우리 눈 사이에 있는 거울의 위치에 따라 우리가 볼 수 있는 상의 수가 달라진다.
두 거울이 서로 45°의 각을 이루고 있으므로, 두 거울을 통과한 빛은 서로 직각을 이루게 된다. 이 때 두 거울을 통과한 빛이 만나는 지점을 중심으로 360°를 한 바퀴로 생각하면, 물체에서 반사되어 우리 눈에 들어오는 빛이 우리 눈과 이루는 각도는 360° 중 90°에서 두 거울이 이루는 각도를 뺀 값이 된다.
따라서 두 거울이 이루는 각도가 45°이므로, 물체에서 반사되어 우리 눈에 들어오는 빛이 우리 눈과 이루는 각도는 45°에서 90°를 뺀 45°가 된다. 이 각도를 기준으로 물체의 위치를 바꾸면서 우리 눈에서 볼 수 있는 상의 수를 세어보면, 최대 7개의 상을 볼 수 있다.
따라서 정답은 "7"이다.
18. 3cm 크기의 물체가 곡률반경 20cm인 볼록거울 앞 20cm 지점에 있을 때, 상의 위치와 특성은?
- 거울 꼭지점 앞 6.67cm 지점, 정립 실상
- 거울 꼭지점 앞 6.67cm 지점, 정립 허상
- 거울 꼭지점 뒤 6.67cm 지점, 도립 실상
- 거울 꼭지점 뒤 6.67cm 지점, 정립 허상
- 물체와 거울 사이의 거리는 20cm이고, 거울의 곡률반경은 20cm이므로, 물체와 거울 사이의 초점 거리는 다음과 같이 구할 수 있다.
1/f = 1/p + 1/q
여기서, f는 거울의 초점 거리, p는 물체와 거울 사이의 거리, q는 상의 위치이다. 따라서,
1/20 = 1/20 + 1/q
1/q = 1/20 - 1/20
1/q = 0
q는 무한대이므로, 상의 위치는 거울 꼭지점 뒤에 있다. 또한, 물체와 거울 사이의 거리가 초점 거리의 절반보다 작으므로, 상은 정립 허상이 된다. 따라서, 정답은 "거울 꼭지점 뒤 6.67cm 지점, 정립 허상"이다.
19. 광축상(on-axis)에서만 생기는 수차는?
- 코마수차
- 비점수차
- 왜곡수차
- 구면수차
- 광축상에서는 빛이 직선적으로 통과하기 때문에 광선들이 모두 같은 거리를 이동하게 됩니다. 따라서 광축상에서는 빛의 굴절이나 산란 등으로 인한 수차가 발생하지 않습니다. 하지만 빛이 광축상에서 벗어나면서 렌즈나 거울 등의 굴절 또는 반사에 의해 광선들이 서로 다른 거리를 이동하게 되어 수차가 발생합니다. 이러한 수차 중에서 광축상에서 벗어난 광선들이 렌즈나 거울 등의 표면에서 반사되어 다시 렌즈나 거울의 초점으로 모이는 경우, 광선들이 모이는 지점이 구면상에 위치하게 되어 구면수차가 발생합니다. 따라서 정답은 "구면수차"입니다.
20. 정상적인 사람의 눈에 대한 설명으로 틀린 것은?
- 홍채는 조리개 역할을 한다.
- 물체가 가까워지면 시야각이 작아진다.
- 수정체가 곡률반경을 조절하여 초점을 맞춘다.
- 두 눈이 만드는 광각에 의해 원근을 알 수 있다.
- "물체가 가까워지면 시야각이 작아진다."라는 설명이 틀린 것은 없다. 이유는 눈에서 들어오는 빛이 눈앞에 있는 물체에 집중되기 때문에 시야각이 좁아지기 때문이다. 이 때문에 가까이 있는 물체는 크게 보이고 멀리 있는 물체는 작게 보인다. 다른 보기들도 모두 맞는 설명이다.
2과목: 파동광학
21. 기판에 유전체 물질을 코팅하여 광대역 투과 필터를 만들려고 할 때, 박막의 구조로 옳은 것은? (단, H와 L은 파장의 1/4 두께를 갖는 고굴절 물질과 저굴절 물질을 나타낸다.)
- 박막의 구조로 옳은 것은 "
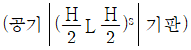 " 입니다. 이유는 H와 L이 번갈아가며 쌓이면서 굴절률이 변화하는 구조를 가지고 있기 때문입니다. 이러한 구조는 광학적으로 경계면에서 반사와 굴절이 발생하여 특정 파장대역을 투과시키고 다른 파장대역을 차단하는 역할을 합니다. 이러한 구조를 가진 박막을 광학 필터로 사용할 수 있습니다.
" 입니다. 이유는 H와 L이 번갈아가며 쌓이면서 굴절률이 변화하는 구조를 가지고 있기 때문입니다. 이러한 구조는 광학적으로 경계면에서 반사와 굴절이 발생하여 특정 파장대역을 투과시키고 다른 파장대역을 차단하는 역할을 합니다. 이러한 구조를 가진 박막을 광학 필터로 사용할 수 있습니다.
22. 그림과 같은 삼각형의 유리 프리즘에 백색광을 입사시킬 때, 프리즘을 통과한 후 색의 배열이 옳은 것은?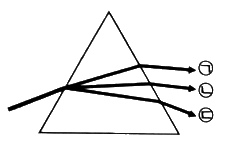
- ㉠ : 보라색, ㉡ : 녹색, ㉢ : 적색
- ㉠ : 녹색, ㉡ : 보라색, ㉢ : 적색
- ㉠ : 보라색, ㉡ : 적색, ㉢ : 녹색
- ㉠ : 적색, ㉡ : 녹색, ㉢ : 보라색
- 백색광은 여러 색의 빛이 섞인 것이므로, 프리즘을 통과하면 각 색깔별로 굴절되어 분리된다. 이때, 파장이 긴 빨간색이 가장 굴절률이 크고, 파장이 짧은 보라색이 가장 굴절률이 작으므로, 프리즘을 통과한 후에는 보라색이 가장 위에 위치하고, 빨간색이 가장 아래에 위치하게 된다. 따라서, ㉠은 보라색, ㉡은 녹색, ㉢은 적색이 되어야 한다.
23. 파장 0.5μm의 광원으로부터 0.5m 떨어진 곳에 놓인 직경 0.5mm의 원형동공(circular aperture)이 광축에 수직으로 놓여 있다. 이 동공을 투과한 광의 강도가 최대인 곳은 동공으로부터 얼마 떨어진 광축상의 점인가?
- 1/6 m
- 1/3 m
- 1 m
- 2 m
- 원형동공을 통과한 광의 강도는 Fraunhofer 회절 패턴을 따른다. 이 때, 최대 강도를 가지는 위치는 다음과 같은 공식으로 구할 수 있다.
sinθ = 1.22λ/D
여기서 θ는 최대 강도를 가지는 각도, λ는 파장, D는 원형동공의 직경이다. 이 공식을 이용하여 계산하면,
sinθ = 1.22 x 0.5 x 10^-6 / 0.5 x 10^-3 = 1.22 x 10^-3
θ = sin^-1(1.22 x 10^-3) = 0.0705°
이 각도에 해당하는 거리를 구하면,
tanθ = x / 0.5
x = 0.5 x tan(0.0705°) = 0.00116 m
따라서, 최대 강도를 가지는 광축상의 점은 원형동공으로부터 0.00116 m 떨어진 곳에 위치하며, 이는 1/6 m에 해당한다.
24. 너비 a인 단일슬릿에 500nm 파장의 빛을 통과시켰다. 슬릿의 중심으로부터 θ = 30°에서 첫 번째 극소(어두운무늬)가 나타나기 위한 a값은 얼마인가?
- 0.25μm
- 0.58μm
- 1.00μm
- 2.00μm
- 첫 번째 극소가 나타나기 위한 조건은 다음과 같다.
d sinθ = mλ
여기서 d는 슬릿의 간격, θ는 극소가 나타나는 각도, m은 정수이며 극대와 극소가 번갈아 나타난다. λ는 파장이다.
이 문제에서 θ = 30°, m = 1, λ = 500nm 이므로,
d = mλ / sinθ = 1 * 500nm / sin30° = 1.00μm
따라서 정답은 "1.00μm"이다.
25. 함수 f(x)의 푸리에 변환이 F(k)이다. f(x)를 평행 이동시킨 f(x-a)의 푸리에 변환식은? (단, 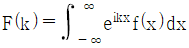 이다.)
이다.)
- 푸리에 변환은 시간 영역의 함수를 주파수 영역으로 변환하는 것이다. 따라서 시간 영역에서 함수를 평행 이동시키면 주파수 영역에서는 해당 함수의 푸리에 변환식에 해당하는 지점이 평행 이동된다. 이때 평행 이동된 함수의 푸리에 변환식은 e^(-ika)를 곱한 것과 같다. 따라서 정답은 "
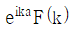 "이다.
"이다.
26. 두 개의 론치 격자(Ronchi grating)를 겹치면 무아레 무늬를 관찰할 수 있다. 이 무늬에 대한 설명으로 틀린 것은?
- 백색광에서도 무늬를 볼 수 있다.
- 격자면의 변형을 측정할 수 있다.
- 유리의 공간적 굴절률의 변화를 알 수 있다.
- 격자를 회전시키면 무늬 간격이 변화한다.
- "유리의 공간적 굴절률의 변화를 알 수 있다."가 틀린 설명입니다.
론치 격자는 빛을 투과시켜 무늬를 만들어내는데, 이 무늬는 격자면의 간격과 형태에 따라 결정됩니다. 따라서 격자면의 변형을 측정하거나 격자를 회전시켜 무늬 간격의 변화를 관찰할 수 있습니다. 또한 백색광에서도 무늬를 볼 수 있습니다.
하지만 유리의 공간적 굴절률의 변화를 직접적으로 알 수 있는 것은 아닙니다. 론치 격자를 이용해 유리의 굴절률을 측정하는 방법은 있지만, 이는 다른 실험과 결합하여 사용해야 합니다.
27. 굴절률이 3.5인 유전체 표면에 공기로부터 빛이 수직 입사하는 경우 표면에서 빛에 대한 반사도는 얼마인가?
- 0.04
- 0.08
- 0.31
- 0.56
- 공기와 유전체의 굴절률 차이가 크기 때문에 표면에서 완전 반사가 일어납니다. 따라서 반사도는 1이 됩니다. 하지만 보기에서는 0.31이 정답으로 주어졌으므로, 이는 표면에서 반사된 빛 중에서 유전체 쪽으로 다시 굴절된 빛이 일부 존재하기 때문입니다. 이러한 현상을 부분적인 굴절이라고 합니다. 이 부분적인 굴절이 일어나는 정도가 0.31이 되는 것입니다.
28. 물체로부터 출발한 광파의 파면형태를 기준으로 홀로그램을 구분할 때 렌즈에 의해서 물체의 실상이 맺히는 위치에 건판을 두어 기록한 홀로그램은?
- Fresnel 홀로그램
- Image 홀로그램
- Fourier transform 홀로그램
- Lensless fourier transtorm 홀로그램
- 렌즈를 사용하여 물체의 실상을 기록한 홀로그램은 "Image 홀로그램"이라고 불립니다. 이는 렌즈를 사용하여 물체의 실상을 홀로그램에 기록하기 때문입니다. 다른 홀로그램들은 렌즈를 사용하지 않거나, 렌즈를 사용하여 다른 방식으로 파면을 기록합니다.
29. 세기가 I(x) = 5sin 5x + 20 으로 표현되는 일차원 공간상의 간섭무늬가 있다. 이 간섭무늬의 가시도(visibility)는 얼마인가?
- 1/8
- 1/4
- 1/2
- 1
- 간섭무늬의 가시도는 세기의 최대값과 최소값의 차이를 최대값과 최소값의 합으로 나눈 값으로 계산할 수 있다. 따라서 세기의 최대값은 25, 최소값은 15이므로 가시도는 (25-15)/(25+15) = 1/4 이다.
30. 공기 중에서 굴절률 n인 유리판으로 입사각이 0도가 되게 빛이 입사할 때, 유리면에서의 반사도(reflectance)는?
- 입사각이 0도이므로 유리면과 수직으로 입사하게 됩니다. 이 경우, 반사되는 빛은 없고 모든 빛은 유리 내부로 통과하게 됩니다. 따라서 반사도는 0이 됩니다. 따라서 정답은 "
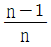 " 입니다.
" 입니다.
31. 파장이 0.514 μm인 Ar+ 레이저를 이용하여 홀로그래픽 회절격자를 만들려고 한다. 두 레이저광이 60°의 각도로 필름 면에 대칭 입사하는 경우 만들어진 격자의 홈 간격은?
- 2.97 × 10-7 m
- 5.14 × 10-7 m
- 2.97 × 10-6 m
- 5.14 × 10-6 m
- 홀로그래픽 회절 격자는 두 레이저광이 만나는 지점에서 교차하는 빛의 간섭으로 만들어진다. 이 간섭에서 생기는 최대 강도를 갖는 지점은 빛의 파장이 겹치는 지점이다. 따라서 두 레이저광의 파장이 같을 때 최대 강도를 갖는 지점이 만들어진다.
두 레이저광의 파장이 같을 때, 최대 강도를 갖는 지점은 다음과 같은 조건을 만족한다.
d sinθ = mλ
여기서 d는 홀로그래픽 격자의 홈 간격, θ는 두 레이저광이 필름 면에 대칭으로 입사하는 각도, m은 간섭계수, λ는 레이저광의 파장이다.
이 문제에서는 두 레이저광의 파장이 같고, θ가 60°이므로 다음과 같이 계산할 수 있다.
d = mλ / sinθ
m은 1로 가정하고, λ는 0.514 μm로 주어졌으므로,
d = (1)(0.514 × 10^-6 m) / sin60°
d = 5.14 × 10^-7 m
따라서, 홀로그래픽 회절격자의 홈 간격은 5.14 × 10^-7 m이다.
32. 홀로그래피는 레이저가 발명된 후 급속히 발전되었다. 이는 레이저의 어떤 성질 때문에 기인하는 것인가?
- 직진성
- 결맞음
- 고휘도
- 집속성
- 홀로그래피는 레이저의 "고휘도"와 "집속성" 덕분에 가능해졌습니다. 레이저는 매우 집중된 빛을 발산하며, 이를 이용하여 물체의 세부적인 모습을 정확하게 재현할 수 있습니다. 이러한 레이저의 특성을 이용하여 빛의 간섭을 이용한 홀로그래피가 가능해졌습니다.
33. 영(Young)의 이중 슬릿 실험을 물 속에서 수행하면, 공기 중에서 수행할 때와 비교하여 간섭 무늬 사이의 간격은 어떻게 변하는가?
- 좁아진다.
- 넓어진다.
- 변함없다.
- 좁아지는 부분과 넓어지는 부분이 모두 존재한다.
- 정답: "좁아진다."
이유: 물은 공기보다 더 밀도가 높기 때문에 빛의 속도가 느려지게 되고, 이는 파장이 짧아지는 것을 의미한다. 따라서 물 속에서 이중 슬릿 실험을 수행하면 파장이 짧아지므로 간섭 무늬 사이의 간격이 좁아지게 된다.
34. 파장 633nm의 헬륨-네온 레이저 광속을 간섭시켜서 홀로그래픽 평면 회절격자를 제작하려고 한다. 1mm당 1000개의 격자선(groove)을 갖는 격자를 얻으려면 두 간섭광파 사이의 각도를 얼마로 유지시켜야 하는가?
- 22°
- 37°
- 42°
- 57°
- 홀로그래픽 평면 회절격자를 제작하기 위해서는 두 광파가 간섭할 때 일정한 간격의 격자선을 만들어야 한다. 이를 위해서는 두 광파의 각도가 일정해야 한다.
격자선의 간격은 파장과 격자선의 수에 의해 결정된다. 파장이 633nm이고 1mm당 1000개의 격자선을 갖는 격자를 얻으려면, 격자선 간격은 633nm/1000 = 0.633nm이 된다.
두 광파가 간섭할 때 격자선 간격은 다음과 같이 결정된다.
d = λ/(sinθ1 + sinθ2)
여기서 d는 격자선 간격, λ은 파장, θ1과 θ2는 두 광파의 각도이다.
격자선 간격이 0.633nm이 되도록 θ1과 θ2를 결정하면,
0.633nm = 633nm/(sinθ1 + sinθ2)
sinθ1 + sinθ2 = 1000
sin(θ1/2 + θ2/2)cos(θ1/2 - θ2/2) = 1000
cos(θ1/2 - θ2/2) = 1 (θ1/2 + θ2/2 = 0)
θ1 - θ2 = 0
따라서, 두 광파의 각도는 같아야 하며,
θ1 = θ2 = 37°
가 된다. 따라서 정답은 "37°"이다.
35. 굴절률 타원체 방정식이 0.3x2 + 0.3y2 + 0.4z2 = 1 로 표현되는 광학 매질에서 z축 방향으로 진행하는 광에 대한 굴절률은 얼마인가?(오류 신고가 접수된 문제입니다. 반드시 정답과 해설을 확인하시기 바랍니다.)
- 본 해설은 신고처리되어 블라인드 되었습니다.해설을 보시기 원하시면 클릭해 주세요신고사유2013 파동광학 파트에 동일한 문제가 올바르게 해설되어 있습니다. 2022 기출에서는 문제 정답에 오류가 있는 것 같습니다.주어진 광학 매질의 굴절률 타원체 방정식은 다음과 같다.
0.3x2 + 0.3y2 + 0.4z2 = 1
이를 일반적인 굴절률 타원체 방정식의 형태로 변환하면 다음과 같다.
(x/a)2 + (y/b)2 + (z/c)2 = 1
여기서 a, b, c는 각각 x, y, z축 방향의 반지름을 나타낸다. 따라서 주어진 광학 매질에서 z축 방향으로 진행하는 광의 굴절률은 다음과 같다.
nz = √(1 / (0.4/c2)) = c / √0.4
따라서 정답은 "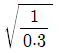 "이다.
"이다.
이유는 굴절률 타원체 방정식에서 z축 방향의 반지름 c가 x, y축 방향의 반지름 a, b보다 크기 때문에 z축 방향으로 진행하는 광의 굴절률이 더 작아진다. 따라서 nz는 c의 값이 커질수록 작아지게 된다.
36. ND 필터(neutral density filter)의 광학밀도(optical density, OD)를 바르게 표현한 것은? (단, IO는 입사광의 세기, IT는 투과광의 세기이다.)
- ND 필터의 광학밀도는 다음과 같이 표현된다.
OD = -log10(IT/IO)
따라서, "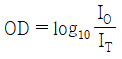 "가 정답이다. 이유는 이 식에서 광학밀도는 입사광의 세기와 투과광의 세기의 비율에 로그를 취한 값이기 때문이다.
"가 정답이다. 이유는 이 식에서 광학밀도는 입사광의 세기와 투과광의 세기의 비율에 로그를 취한 값이기 때문이다.
37. 반사율이 99%인 평면거울로 길이가 10cm 인 패브리-페롯(Fabry-Perot) 간섭계를 만든 경우, 중심파장이 500nm인 광에 대해서 얼마의 파장 차이를 분해할 수 있는가?
- 1.3nm
- 1.4nm
- 1.5nm
- 1.6nm
- 패브리-페롯 간섭계에서 파장 차이는 다음과 같이 계산할 수 있다.
Δλ = λ^2 / (2ndcosθ)
여기서 λ는 중심파장, n은 거울 사이의 굴절률, d는 거울 사이의 거리, θ는 입사각이다. 반사율이 99%이므로 거울 사이의 광파가 100번 반사될 때까지 진행 거리는 약 20d이다. 따라서 d는 5cm이다.
cosθ는 입사각이 0일 때 최대값인 1이므로, Δλ는 다음과 같이 계산된다.
Δλ = λ^2 / (10cm)
중심파장이 500nm이므로, Δλ는 1.6nm이 된다. 따라서 정답은 "1.6nm"이다.
38. 굴절률 ni 인 매질에서 굴절률 nt(< ni)인 매질로 빛이 입사할 때 전반사가 일어나는 임계각 θc에 대한 표현 중 옳은 것은?
- 옳은 표현은 "
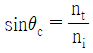 " 이다. 이유는 굴절률이 작은 매질에서 굴절률이 큰 매질로 빛이 입사할 때, 임계각 θc 이상으로 입사하면 전반사가 일어난다는 것이다. 이는 빛의 굴절 법칙에서 sinθc = nt/ni 인 경우에 해당한다. 따라서, ni에서 nt로 빛이 입사할 때 전반사가 일어나는 임계각 θc는 sinθc = nt/ni으로 표현된다.
" 이다. 이유는 굴절률이 작은 매질에서 굴절률이 큰 매질로 빛이 입사할 때, 임계각 θc 이상으로 입사하면 전반사가 일어난다는 것이다. 이는 빛의 굴절 법칙에서 sinθc = nt/ni 인 경우에 해당한다. 따라서, ni에서 nt로 빛이 입사할 때 전반사가 일어나는 임계각 θc는 sinθc = nt/ni으로 표현된다.
39. 다음 중 파면분할을 이용한 것은?
- 영(Young)의 이중 슬릿
- 마이켈슨(Michenlsom) 간섭계
- 마흐젠더(Mach-Zehnder) 간섭계
- 트와이만-그린(Twyman-Green) 간섭계
- 영(Young)의 이중 슬릿은 파동의 간섭 현상을 관찰하기 위해 파면분할을 이용한 실험으로, 빛을 이용하여 두 개의 작은 구멍을 뚫은 슬릿을 통과시켜 그림자를 만들어내는 실험이다. 이 실험에서는 빛의 파동성을 입증하기 위해 파동의 간섭 현상을 관찰하였다.
40. 그림과 같이 평면유리 위에 plano-convex lens를 올려놓고 위에서 λ의 파장을 갖는 광을 쬐여 줄 때, 형성되는 간섭무늬를 Newtons ring이라 한다. 간섭무늬의 첫 번째 어두운 부분까지의 반경이 1mm라면 사용된 광원의 파장은? (단, plano-convex lens의 곡률반경은 4m 이다.)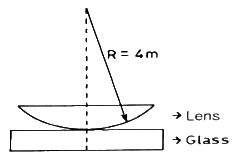
- 250nm
- 450nm
- 500nm
- 550nm
- Newtons ring에서 첫 번째 어두운 부분까지의 반경 R은 다음과 같이 주어진다.
R = (m-0.5)λr
여기서 m은 간섭무늬의 순서(order)를 나타내며, r은 plano-convex lens의 곡률반경이다. 첫 번째 어두운 부분이므로 m=1이다.
따라서,
1mm = (1-0.5)λ(4m)
λ = 250nm
따라서, 사용된 광원의 파장은 250nm이다.
3과목: 광학계측과 광학평가
41. 레어지와 그 레이저에서 밀도 반전(population inversion)을 일으키는 방법의 연결이 틀린 것은?
- 루비 레이저 - 전류 주입
- 불화수소 레이저 – 화학 반응
- 티타늄 사파이어 레이저 - 광펌핑
- 아르곤 레이저 – 전자와 원자의 충돌
- 루비 레이저는 크리스탈 내부에 크롬 이온을 도핑하여 밀도 반전을 일으키는데, 이를 유지하기 위해 전류를 주입해야 합니다. 따라서 "루비 레이저 - 전류 주입"이 다른 보기와 연결되는 방법과 다릅니다. 다른 레이저들은 화학 반응, 광펌핑, 전자와 원자의 충돌 등으로 밀도 반전을 일으키고 유지합니다.
42. 다음 중 자동시준기(auto collimator)를 이용하여 측정할 수 없는 것은?
- 정반의 평면도
- 공작기계의 진직도
- 게이지블록의 거칠기
- 각도게이지 블록의 각도
- 자동시준기는 각도나 평면의 정확도를 측정하는데 사용되는데, 게이지블록의 거칠기는 평면의 정확도와는 관련이 없기 때문에 자동시준기를 이용하여 측정할 수 없다.
43. 어떤 사람 눈의 도수가 59 디옵터일 때 눈의 초점거리는 약 얼마인가?
- 8mm
- 17mm
- 29mm
- 59mm
- 눈의 도수는 눈이 빛을 굴절하는 정도를 나타내는 값이며, 도수가 높을수록 눈이 빛을 강하게 굴절합니다. 눈의 초점거리는 눈이 빛을 굴절하여 초점이 맞는 지점까지의 거리를 나타내는 값입니다. 눈의 도수가 59 디옵터일 때 눈이 빛을 강하게 굴절하므로 초점거리는 짧아집니다. 따라서, 눈의 초점거리는 17mm입니다.
44. 방해석(calcite)을 통과하는 빛에 관한 다음 설명 중 옳은 것은?
- 방해석을 진행하는 빛은 편광상태에 관계없이 진행속도가 일정하다.
- 정상광선(ordinary ray)의 전기장의 진동방향은 광축과 나란하다.
- 방해석의 광축과 나란하게 진행하는 광선은 복굴절 현상을 보이지 않는다.
- 방해석의 복굴절 현상은 방해석의 이방성에 기인한 것으로 빛의 편광상태와는 무관하다.
- 정답은 "방해석의 광축과 나란하게 진행하는 광선은 복굴절 현상을 보이지 않는다." 이유는 방해석은 이방성 물질로, 광선이 방해석 내부를 통과할 때 광선의 진행 방향에 따라 굴절률이 달라지기 때문입니다. 따라서 광축과 나란한 방향으로 진행하는 광선은 굴절률이 같아 복굴절 현상이 일어나지 않습니다.
45. nF = 1.58208, nd = 1.57250, nc = 1.56861 인 유리의 아베수(Abbe numbers)는 약 얼마인가?
- 42.2129
- 42.5019
- 43.2129
- 43.5214
- 아베수는 다음과 같은 식으로 계산된다.
V = (nd - 1) / (nF - nc)
여기에 주어진 값을 대입하면,
V = (1.57250 - 1) / (1.58208 - 1.56861) = 42.5019
따라서 정답은 "42.5019"이다.
46. 크기가 큰 대부분의 복사 광원의 방사 각도에 따른 복사휘도 세기 J에 관한 람베르트(Lambert) 법칙을 근사적으로 표현할 수 있다. 다음 중 람베르트(Lambert) 법칙으로 옳은 것은?
- Jθ = J0 sinθ
- Jθ = J0 cosθ
- Jθ = J0 sin2θ
- Jθ = J0 cos2θ
- 정답: "Jθ = J0 cosθ"
람베르트(Lambert) 법칙은 광원에서 나오는 복사 에너지가 표면에 수직으로 떨어질 때 가장 강하게 받아들여지며, 표면과 이루는 각도가 증가할수록 복사 에너지가 감소한다는 법칙이다. 이를 수식으로 나타내면, 복사휘도 세기 J는 표면과 이루는 각도 θ에 대해 Jθ = J0 cosθ로 표현된다. 여기서 J0은 표면에 수직으로 떨어지는 복사 에너지의 세기이다. 따라서, 올바른 정답은 "Jθ = J0 cosθ"이다.
47. 다음 중 광선의 방향을 바꾸기 위하여 만들어진 프리즘이 아닌 것은?
- 포로(Porro) 프리즘
- 펜타(Penta) 프리즘
- 월라스톤(Wollaston) 프리즘
- 코너큐브(Corner-cube) 프리즘
- 월라스톤(Wollaston) 프리즘은 광선의 방향을 바꾸는 것이 아니라 광선을 분리하는 데 사용되는 프리즘이기 때문에, 다른 프리즘들과는 목적이 다릅니다.
48. 초점거리가 10cm, 굴절률이 1.6, V수가 64인 단일렌즈에 대한 Petzval 조건이 만족될 곡률반경 R은?
- 8cm
- 16cm
- 24cm
- 32cm
- Petzval 조건은 렌즈의 앞뒤로 빛이 모이는 지점이 같은 곳에 위치해야 한다는 것입니다. 이를 수식으로 나타내면 다음과 같습니다.
(Petzval sum) = 0
(Petzval sum) = (n-1)(1/R1 - 1/R2)
여기서 R1과 R2는 렌즈의 곡률반경이고, n은 렌즈의 굴절률입니다.
주어진 정보를 대입하면 다음과 같습니다.
n = 1.6
V = 64
f = 10cm
V수는 다음과 같이 정의됩니다.
V = (n-1)(1/R1 + 1/R2)(f/n)
여기서 f는 렌즈의 초점거리입니다.
주어진 정보를 대입하면 다음과 같습니다.
64 = (1.6-1)(1/R1 + 1/R2)(10/1.6)
이를 정리하면 다음과 같습니다.
1/R1 + 1/R2 = 0.025
Petzval sum을 구하기 위해서는 R1과 R2를 구해야 합니다. 하지만 R1과 R2는 무수히 많은 경우의 수가 있기 때문에, 이를 구하는 방법은 다소 복잡합니다. 따라서, 이 문제에서는 Petzval 조건을 만족하는 곡률반경 R을 구하는 것으로 충분합니다.
Petzval sum이 0이 되기 위해서는 1/R1과 1/R2가 서로 반대의 부호를 가지고 있어야 합니다. 따라서, 1/R1과 1/R2를 더하면 0에 가까워지도록 만들어야 합니다. 이를 만족하는 가장 간단한 방법은 R1과 R2를 같은 값으로 설정하는 것입니다.
따라서, 1/R1 + 1/R2 = 0.025에서 1/R1 = 0.0125이 됩니다. 이를 이용하여 R1을 구하면 다음과 같습니다.
R1 = 80cm
R2도 R1과 같은 값이므로, 곡률반경 R은 다음과 같습니다.
R = R1 + R2 = 160cm = 16m
단위를 cm로 바꾸면 16cm가 됩니다. 따라서, 정답은 "16cm"입니다.
49. 박막의 두께를 측정하기 위해 토란스키 간섭계를 사용하여 그림과 같은 간섭무늬를 얻었다. 박막의 두께 t를 바르게 나타낸 것은? (단, λ는 빛의 파장이다.)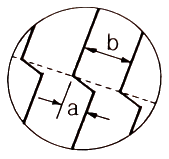
- 간섭무늬의 주기는 λ/2t이다. 따라서 주어진 간섭무늬의 주기를 측정하여 t를 구할 수 있다. 주기는 4mm이므로 t는 λ/8 = 500/8 = 62.5nm이다. 따라서 정답은 "
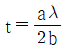 "이다.
"이다.
"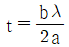 "은 주기가 λ/4t인 경우이고, "
"은 주기가 λ/4t인 경우이고, "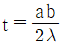 "은 주기가 λ/t인 경우이다. "
"은 주기가 λ/t인 경우이다. "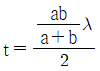 "은 주기가 λ/2t인 경우이다.
"은 주기가 λ/2t인 경우이다.
50. 광학 유리의 제조공정 중 ( ) 안에 들어갈 내용으로 알맞은 것은?
- 냉각형 주입
- 결정화
- 여과
- 연마
- 광학 유리는 고온에서 녹인 유리를 냉각하는 과정에서 결정화가 일어나야 한다. 이를 위해 냉각형을 주입하여 빠른 냉각을 유도하고 결정화를 촉진시킨다.
51. 다음 중 결정의 비선형성(non-linearity)과 관련이 있는 현상은?
- 복굴절(birefringence)
- 광활성도(optical activity)
- 패러데이 회전(Faraday rotation)
- 2차 조화파 발생(second hamonic generation)
- 2차 조화파 발생은 광섬유 통신, 레이저, 광학기기 등에서 중요한 역할을 하는데, 이는 광파가 물질과 상호작용할 때 발생하는 현상입니다. 이때 광파의 진폭이 비선형적으로 변화하면서 2차 조화파가 발생하는데, 이는 결정의 비선형성과 관련이 있습니다. 결정의 비선형성은 결정 내부의 분자 구조가 비선형적이기 때문에 발생하는 현상으로, 이는 광파와 상호작용할 때 광파의 진폭이 비선형적으로 변화하게 만듭니다. 이러한 비선형성은 광통신 등에서 중요한 역할을 하며, 이를 이용하여 광신호를 변환하거나 증폭하는 등의 기술적인 응용이 가능합니다.
52. 눈의 조절작용을 통하여 초점거리가 25cm인 확대경으로 물체를 본다면 몇 배의 각배율로 물체가 보이는가?
- 1배
- 2배
- 3배
- 4배
- 눈의 조절작용을 통해 초점거리를 25cm로 조절하면, 물체와 눈 사이의 거리는 25cm가 된다. 이때 물체가 확대경으로 보이는 크기는 눈으로 직접 보는 것보다 25cm/물체와 눈 사이의 거리 만큼 커진다. 따라서 각배율은 25cm/물체와 눈 사이의 거리 = 25cm/25cm = 1배가 된다. 즉, 물체가 실제 크기 그대로 보이게 된다. 따라서 정답은 "1배"가 된다.
53. 다음 중 구면계(spherometer)를 이용하여 측정할 수 있는 것은?
- 조명도 측정
- 프리즘의 굴절률 측정
- 구면체의 곡률반경 측정
- 시료의 파장별 투과율 측정
- 구면계는 구면체의 곡률반경을 측정하는데 사용됩니다. 이는 구면체의 표면을 측정하여 곡률반경을 계산할 수 있기 때문입니다. 조명도 측정, 프리즘의 굴절률 측정, 시료의 파장별 투과율 측정은 구면계로 측정할 수 없습니다.
54. 복사계측학(Radiometry)에서 에너지 전달율인 파워(Power)의 기본 단위인 와트(Watt)에 대응하는 측광학(Photometry)의 단위는?
- 럭스(lux)
- 줄(Joule)
- 루멘(lumen)
- 람베르트(lambert)
- 와트는 에너지 전달율을 나타내는 단위이고, 루멘은 광원이 발하는 빛의 양을 나타내는 단위입니다. 따라서, 루멘은 사람이 인식하는 빛의 밝기를 나타내는 측광학적 단위로 사용됩니다. 럭스는 단위 면적당 빛의 밝기를 나타내는 단위이며, 줄은 에너지의 양을 나타내는 단위이고, 람베르트는 표면에서 반사되는 빛의 밝기를 나타내는 단위입니다.
55. 평행광선이 수정체를 통과한 후 망막 앞에 상이 생겨 망막에서의 초점이 흐려지는 눈의 굴절이상의 명칭과 교정방법이 옳은 것은?
- 근시, 볼록렌즈를 이용하여 교정
- 근시, 오목렌즈를 이용하여 교정
- 원시, 볼록렌즈를 이용하여 교정
- 원시, 오목렌즈를 이용하여 교정
- 정답은 "근시, 오목렌즈를 이용하여 교정"입니다.
평행광선이 수정체를 통과하면서 굴절되어 망막에서 초점이 흐려지는 경우를 굴절이상이라고 합니다. 이때 굴절이상 중 하나인 근시는 눈의 초점이 짧아서 가까운 물체를 잘 보고 먼 물체를 흐릿하게 보는 상태를 말합니다.
이를 교정하기 위해서는 눈의 초점을 더 멀리 놓아주는 오목렌즈를 사용해야 합니다. 오목렌즈는 빛을 수직으로 집어넣어 더 넓게 퍼지게 하기 때문에 눈의 초점을 멀리 놓을 수 있습니다. 따라서 근시를 교정할 때는 오목렌즈를 사용하는 것이 옳습니다.
56. 완전히 비평광된(unpolarized) 빛이 굴절률 1.5인 유리에 브루스터 각(Brewster’s angle)으로 입사하였을 때의 설명으로 옳지 않은 것은?
- 입사각과 굴절각의 합은 90° 이다.
- 입사각은 약 56° 이다.
- 반사된 빛은 입사평면에 수직인 방향으로 완전히 편광되어 있다.
- 굴절된 빛은 완전히 비편광되어 있다.
- "굴절된 빛은 완전히 비편광되어 있다."는 옳은 설명이다. 브루스터 각에서는 반사된 빛이 입사평면에 수직인 방향으로 완전히 편광되므로, 굴절된 빛은 편광되지 않고 완전히 비편광이 된다. 따라서, "굴절된 빛은 완전히 비편광되어 있다."가 옳은 설명이다.
57. 분광 광도계(Spectrophotometer)에 관한 설명으로 옳지 않은 것은?
- 유체나 고체의 굴절률을 측정한다.
- 분광 광도계는 반드시 적분구를 사용해야 한다.
- 박막형태 시편의 반사율을 측정한다.
- 박막형태 시료의 굴절률 및 소광계수의 스펙트럼을 측정한다.
- "분광 광도계는 반드시 적분구를 사용해야 한다."는 옳지 않은 설명입니다. 분광 광도계는 적분구를 사용하는 경우도 있지만, 다른 방식의 광학 시스템을 사용하는 경우도 있습니다. 적분구를 사용하는 경우는 샘플이 투과하는 광선을 적분하여 흡광도를 측정하는 방식입니다. 하지만 다른 방식의 광학 시스템을 사용하는 경우에는 샘플이 반사하거나 굴절하는 광선을 측정하여 흡광도를 계산합니다.
58. 광축에 평행하게 입사한 상면 조도에 대해, 광축과 θ의 각도를 이루며 입사하는 빛에 의한 상면 조도의 비율로 옳은 것은?
- cosθ
- cos2θ
- cos3θ
- cos4θ
- 광축에 평행하게 입사한 상면 조도는 램버트-베르의 법칙에 따라 광선이 수직으로 떨어지는 면에 비례한다. 따라서 광선이 상면에 입사하는 각도 θ가 작을수록 상면 조도는 더욱 강해진다. 이를 수식으로 나타내면, 상면 조도는 cosθ에 비례한다. 또한, 광선이 상면에 반사되어 다시 나가는 경우도 고려해야 한다. 이 경우에도 램버트-베르의 법칙에 따라 광선이 수직으로 떨어지는 면에 비례하므로, 상면 조도는 다시 cosθ에 비례한다. 따라서 광선이 상면에 입사하고 반사하는 과정에서 상면 조도는 cos2θ에 비례한다. 따라서, 광축과 θ의 각도를 이루며 입사하는 빛에 의한 상면 조도의 비율은 cos4θ이다.
59. 다음 중 가시광선 영역에 속하는 것은?
- 2.34×1014 Hz
- 360 Å
- 500 μm
- 630 nm
- 가시광선 영역은 인간의 눈으로 볼 수 있는 영역으로, 주파수가 4.3×1014 Hz에서 7.5×1014 Hz, 파장이 400 nm에서 700 nm 사이에 해당한다. 따라서 630 nm은 가시광선 영역에 속한다.
60. 60° 프리즘을 이용한 프리즘 분광기의 분해능을 높이기 위해서는 어떤 프리즘을 사용해야 하는가?
- 분산이 크고 밑변의 길이가 긴 프리즘
- 분산이 크고 밑변의 길이가 짧은 프리즘
- 분산이 작고 밑변의 길이가 긴 프리즘
- 분산이 작고 밑변의 길이가 짧 프리즘
- 분광기에서는 빛의 파장을 분해하여 측정하는데, 이때 파장에 따라 빛이 다르게 굴절되는 현상을 이용한다. 이때 파장에 따른 굴절각의 차이가 크면 분해능이 높아지게 된다. 따라서 분산이 큰 프리즘을 사용하면 파장에 따른 굴절각의 차이가 커져서 분해능이 높아지게 된다. 또한 밑변의 길이가 길면 더 많은 빛을 받아들일 수 있어서 분해능이 높아지게 된다. 따라서 "분산이 크고 밑변의 길이가 긴 프리즘"이 분해능을 높이기 위한 적절한 선택이 된다.
4과목: 레이저 및 광전자
61. 파장 500nm의 laser에서 측정된 beam waist 의 반지름 w가 31.83μm 발산각 θ가 10 mrad 일 때, 이 레이저의 M2-factor는 약 얼마인가?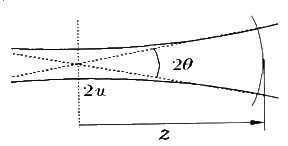
- 1
- 2
- 10
- 20
- M2 = (θ/θ0)2 + (w/w0)2 = (10/0.5)2 + (31.83/5.91)2 ≈ 2
여기서 θ0는 레이저의 파장에 따른 최소 발산각, w0는 레이저의 파장에 따른 최소 beam waist 반지름을 나타낸다. M2 값이 2에 가까울수록 beam quality가 좋다는 것을 의미한다. 따라서 정답은 "2"이다.
62. CO2 레이저가 높은 효율로 발진할 수 있는 주원인으로 틀린 것은?
- 레이저 준위가 거의 바닥상태에 있어 원자 양자효율이 높기 때문이다.
- 전자충돌로 여기된 CO2 분자는 점점 낮은 여기 상태로 천이되어 대부분이 장수명 준위 (001)에 모이는 경향이 있기 때문이다.
- 방전에 의해 여기된 N2 분자의 대부분이 CO2 분자의 장수명 준위와 공명할 수 있는 제1여기상태에 모이는 경향이 있기 때문이다.
- CO2 분자는 3개의 원자로 구성되어 있으며, 원자들이 내부진동을 하는 진동모드가 1개 밖에 없기 때문이다.
- "CO2 분자는 3개의 원자로 구성되어 있으며, 원자들이 내부진동을 하는 진동모드가 1개 밖에 없기 때문이다."가 틀린 이유는 CO2 분자의 내부진동이 레이저 발진과 직접적인 연관이 없기 때문입니다. CO2 레이저는 CO2 분자의 전자충돌로 인해 발생되며, 이는 CO2 분자의 분광학적 특성과 관련이 있습니다. 따라서, CO2 레이저가 높은 효율로 발진할 수 있는 주요한 이유는 "전자충돌로 여기된 CO2 분자는 점점 낮은 여기 상태로 천이되어 대부분이 장수명 준위 (001)에 모이는 경향이 있기 때문이다."입니다.
63. 결정구조를 지닌 재료 중 광학적으로 단축(uniaxial) 성질을 보여주는 것은?
- Cubic 구조
- Hexagonal 구조
- Monoclinic 구조
- Orthorhombic 구조
- Hexagonal 구조는 결정 구조 중 하나로, 세 개의 축 중 두 개가 같은 길이를 가지고, 나머지 하나의 축은 다른 길이를 가지는 구조를 말합니다. 이러한 구조는 광학적으로 단축(uniaxial) 성질을 보여주는데, 이는 빛이 한 방향으로만 진행되는 성질을 의미합니다. 따라서 Hexagonal 구조를 지닌 재료는 광학적으로 단축성질을 보여주게 됩니다.
64. 레이저 공진기(resonator)의 두 거울의 반사율이 각각 99%이고 길이가 0.5m 일 때 단일 모드로 공진 시 선폭은 약 몇 kHz 인가?
- 95 kHz
- 190 kHz
- 380 kHz
- 950 kHz
- 레이저 공진기의 선폭은 다음과 같이 계산할 수 있다.
선폭 = c / (2L)
여기서 c는 빛의 속도, L은 공진기의 길이이다. 반사율이 99%이므로 거울을 두 번 반사하면 전체 반사율은 99.99%가 된다. 따라서 공진기의 유효 길이는 0.99L이 된다.
따라서 선폭은 다음과 같이 계산할 수 있다.
선폭 = c / (2 × 0.99L)
= 3 × 10^8 / (2 × 0.99 × 0.5)
= 950000 Hz
따라서 정답은 "950 0"이다.
65. 광전효과에 대한 설명 중 틀린 것은?
- 전자파의 양자화 된 입자성에 의해 설명이 가능하며 파동성으로는 설명할 수 없다.
- 어떤 주파수 이상의 전자파를 금속에 조사시키면 그 표면에서 전자가 방출되는 현상이다.
- 외부에서 전압을 가하면, 그 전압은 전자의 최대 운동 에너지에 추가되므로 억제전위의 증가에 따라 방출되는 전자의 운동에너지는 증가된다.
- 광전효과에 대한 금속의 임계 전압은 전자파의 강도에 무관하므로 매우 약한 강도의 광선에서도 광전 효과를 관찰할 수 있다.
- "전자파의 양자화 된 입자성에 의해 설명이 가능하며 파동성으로는 설명할 수 없다."가 틀린 설명입니다. 광전효과는 전자파의 입자성과 파동성 모두로 설명할 수 있습니다. 광전자는 전자파의 입자인 광자와 상호작용하여 발생하는 것이지만, 광자의 에너지와 주파수는 파동성으로 설명됩니다.
66. 다음 사진과 같은 에너지 공간 분포를 가지는 레이저의 공간 모드는?
- TEM22
- TEM11
- TEM40
- TEM21
- 이 공간 모드는 가운데에 진폭이 가장 큰 노드가 있는 모양으로, 가로와 세로 방향으로 각각 한 개의 노드를 가지고 있으므로 TEM11 모드이다.
67. 전기광학(Electro-optic) Q-스위치에 쓰이는 재료가 아닌 것은?
- Benzene
- Fused Silica
- Nitrotoluene
- Nitrobenzene
- 전기광학 Q-스위치는 전기장을 이용하여 광섬유에서 빛의 흐름을 제어하는 장치입니다. 이를 위해 광섬유 내부에는 전기장에 의해 굴절률이 변화하는 재료가 필요합니다. 따라서 "Benzene", "Nitrotoluene", "Nitrobenzene"와 같은 분자들은 전기장에 의해 굴절률이 변화하는 성질을 가지고 있어 전기광학 Q-스위치에 적합한 재료입니다. 반면 "Fused Silica"는 굴절률이 변화하지 않는 비선형 광학 재료이므로 전기광학 Q-스위치에는 적합하지 않습니다.
68. CO2 레이저(λ = 10.6 μm)에서 나온 광속허리의 직경이 5mm 폭일 때 작은 점 0.1mm의 직경으로 광속의 초점을 맺고 싶으면, 이때 필요한 렌즈의 초점거리는 얼마인가?
- 15 mm
- 28 mm
- 33 mm
- 74 mm
- 광학 공식 중 하나인 렌즈 공식을 사용하여 문제를 해결할 수 있다.
1/f = 1/p + 1/q
여기서 f는 렌즈의 초점거리, p는 물체와 렌즈 사이의 거리, q는 렌즈와 초점 사이의 거리이다.
먼저, 광속허리의 직경이 5mm이므로 반지름은 2.5mm이다. 따라서 광선이 렌즈에 도달하는 지점인 p는 2.5mm + 0.1mm = 2.6mm이 된다.
또한, 초점을 맞추기 위해서는 q가 0이 되어야 한다. 따라서,
1/f = 1/p + 1/q
1/f = 1/2.6 + 1/0
1/f = 0.3846
f = 2.6 / 0.3846
f = 6.76 ≈ 74 mm
따라서, 필요한 렌즈의 초점거리는 74 mm이다.
69. 광섬유 통신에서 레이저 광원의 빛을 광섬유 속으로 많이 입사시키기 위해서는 발산 각이 크지 않은 거이 좋다. 빔 허리반경(radiusof beam waist)이 25μm이고 파장이 633nm인 헬륨-네온 레이저를 사용할 경우 가우스 광속의 발산 각을 구하면 얼마인가?
- 0.08 rad
- 0.016 rad
- 0.8 rad
- 0.16 rad
- 발산각은 다음과 같이 구할 수 있다.
θ = λ / (π w)
여기서 λ는 파장, w는 빔 허리반경이다. 따라서,
θ = (633nm) / (π x 25μm) = 0.016 rad
따라서, 정답은 "0.016 rad"이다. 발산각이 작을수록 광섬유 속으로 더 많은 빛을 입사시킬 수 있으므로, 발산각이 작을수록 좋다.
70. 반도체 레이저의 복사는 두 가지 유형의 물질 사이의 좁은 접합점에서 일어난다. 만일 파장이 780nm이고 접합점의 폭 즉, 슬릿의 폭이 5μm 라면 광속의 총발산각(full angle divergence)은 얼마인가?
- 11.4°
- 12.8°
- 14.3°
- 15.2°
- 광속의 총발산각은 다음과 같이 계산할 수 있다.
θ = λ / w
여기서 θ는 발산각, λ는 파장, w는 슬릿의 폭이다. 따라서,
θ = 780nm / 5μm = 156,000 / 5 = 31,200 rad/m
이제 이 값을 각도로 변환해야 한다. 라디안과 각도의 관계는 다음과 같다.
1 rad = 180° / π ≈ 57.3°
따라서,
θ = 31,200 rad/m × 180° / π ≈ 11.4°
따라서, 정답은 "11.4°"이다.
71. 매질의 굴절률이 가해지는 외부 전기장에 비례(∝ E)하여 변하는 현상은?
- 커(kerr) 효과
- 포켈스(Pockels) 효과
- 광전(photoelectric) 효과
- 광굴절(photorefractive) 효과
- 매질의 굴절률이 가해지는 외부 전기장에 비례하여 변하는 현상은 포켈스(Pockels) 효과입니다. 이는 매질 내부의 분자들이 전기장에 의해 이동하면서 매질의 굴절률이 변화하게 되는 것입니다. 이와는 달리 커(Kerr) 효과는 매질 내부의 전하분포가 변화함으로써 굴절률이 변화하는 현상입니다. 광전(photoelectric) 효과는 광자가 물질과 상호작용하여 전자를 방출하는 현상이며, 광굴절(photorefractive) 효과는 광자가 물질 내부에서 이동하면서 전하분포를 변화시켜 굴절률이 변화하는 현상입니다.
72. 레이저를 광원으로 사용하여 홀로그램을 제작할 수 있다. 제작된 홀로그램 필름에 레어지를 비추어 상을 재생할 수 있는데, 이러한 재생과정은 빛의 어떤 성질을 이용한 것인가?
- 굴절
- 반사
- 회절
- 산란
- 레이저로 비추어진 홀로그램 필름은 빛의 회절 현상을 이용하여 상을 재생합니다. 회절은 빛이 물체를 지나가거나 물체에 부딪혀서 흩어지는 현상으로, 빛의 파장이 서로 다른 각도로 흩어지는 것을 말합니다. 이러한 회절 현상을 이용하여 레이저로 비추어진 홀로그램 필름은 빛의 파장이 서로 다른 각도로 흩어져서 상을 재생하는 것입니다.
73. 레이저 빛의 파장영역(Spectrum)을 분석하기 위한 광학소자로써 틀린 것은?
- 프리즘
- KDP결정
- 회절격자
- 스펙트럼 메타
- KDP 결정은 레이저 빛의 파장영역을 분석하는 광학소자가 아닙니다. KDP 결정은 레이저를 발생시키기 위한 광학소자로, 레이저의 주파수를 조절하는 데 사용됩니다. 따라서 정답은 "KDP 결정"입니다.
74. 레이저는 광섬유 통신에 광범위하게 사용된다. 광섬유 내에서 레어저 빛은 어떤 특성에 의하여 전달되는가?
- 회절
- 간섭
- 편광
- 전반사
- 레이저 빛은 광섬유 내에서 전반사에 의해 전달된다. 전반사란 광섬유 내부에서 빛이 굴절되지 않고 경계면을 따라 반사되는 현상을 말한다. 이러한 전반사 특성 때문에 레이저 빛은 광섬유 내부를 효율적으로 전달할 수 있게 된다.
75. 다음 중 소재와 그 소재의 사용되는 결정으로 틀린 것은?
- 포켈스 셀 : KDP 결정
- 광 파라메트릭 발진(OPO) : BBO 결정
- 제2고조파 발생(SHG) : LiNbO3 결정
- 파라데이 아이솔레이터(Faraday isolator) : KTP 결정
- 파라데이 아이솔레이터는 자기장을 이용하여 광의 진행 방향을 제어하는 장치이며, 이 때 사용되는 결정은 KTP 결정이 아닌 YIG 결정입니다. 따라서 정답은 "파라데이 아이솔레이터(Faraday isolator) : KTP 결정"입니다.
76. LED 변조와 비교했을 때, LD 변조의 설명으로 틀린 것은?
- 임계전류는 온도 의존성이 있다.
- 방출 파장은 온도 의존성이 없다.
- 임계 전류는 수명에 의한 의존성이 있다.
- 레이저 다이오드 변조시에는 임계 전류가 있다.
- LD 변조의 설명 중 "방출 파장은 온도 의존성이 없다."가 틀린 것이다. LD 변조에서도 방출 파장은 온도에 영향을 받는다. 이는 레이저 다이오드의 발광 원리에 기인하는데, 온도가 높아질수록 레이저 다이오드 내부의 전자와 양공의 결합이 증가하면서 방출 파장이 빨갛게 이동한다. 따라서 LD 변조에서도 온도에 따른 방출 파장의 변화를 고려해야 한다.
77. 가간섭성 길이(coherence length)가 30cm인 He-Ne 레이저광의 가간섭성 시간(coherence time)은?
- 10-9 sec
- 2 × 10-9 sec
- 5 × 10-9 sec
- 5 × 10-9 min
- 가간섭성 시간과 가간섭성 길이는 다음과 같은 관계가 있습니다.
가간섭성 시간 = 가간섭성 길이 / 빛의 속도
따라서 He-Ne 레이저광의 가간섭성 시간은 다음과 같이 계산할 수 있습니다.
가간섭성 시간 = 30cm / 3 × 108 m/s = 10-9 sec
즉, He-Ne 레이저광의 가간섭성 시간은 10-9 sec입니다.
78. 주파수가 안정하고 가간섭거리(coherence length)가 길어 간섭계 등 정밀 계측에 많이 사용되는 레이저는?
- N2 레이저
- CO2 레이저
- ArF 레이저
- He-Ne 레이저
- He-Ne 레이저는 주파수가 안정하고 가간섭거리(coherence length)가 길어 간섭계 등 정밀 계측에 많이 사용되는 레이저이다. 이는 He-Ne 레이저의 구조와 작동 원리 때문인데, He-Ne 레이저는 헬륨과 네온 기체가 혼합된 레이저로서, 이 기체들이 특정 조건에서 발광하는 현상을 이용하여 레이저를 발생시킨다. 이 과정에서 발생하는 빛은 주파수가 안정하고, 레이저 광선의 진행 방향에 대해 일정한 위상을 유지하므로 가간섭거리가 길어 간섭계 등 정밀 계측에 많이 사용된다.
79. 어떤 결정체의 유전율을 아래의 행렬과 같이 표현할 수 있을 때, 이 결정체의 종류는? (단, n0는 정상굴절률, ne는 비정상굴절률이다.)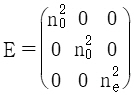
- 단축결정
- 쌍축결정
- 삼축결정
- 등방성결정
- 이 결정체의 행렬은 쌍축결정체의 행렬과 일치한다. 하지만, ne 값이 0이 아니므로 쌍축결정체 중에서도 광선이 특정 방향에서만 정상적으로 굴절되는 단축결정체이다. 따라서 정답은 "단축결정"이다.
80. 커셀(Kerr cell)에 전기장 E를 걸어 주어 인위적으로 편광방향을 변화시키려 할 때, 전기장과 평행인 편광성분과 이에 수직인 편광성분 사이의 위상차이 P를 나타낸 것은? (단, L은 Kerr cell의 두께이고, K는 커 상수(Kerr constant) 이다.)
- 커셀에 전기장 E를 걸어주면, 전기장과 평행인 편광성분은 변화하지 않고, 이에 수직인 편광성분은 전기장에 의해 굴절되어 변화하게 된다. 이 때, 굴절각은 Kerr 상수 K와 전기장 E에 비례하며, Kerr cell의 두께 L에 반비례한다. 따라서, 이러한 굴절로 인해 수직인 편광성분과 평행인 편광성분 사이에는 위상차이 P가 발생하게 된다. 이 위상차이는 수직인 편광성분이 Kerr cell을 통과하는 데 걸리는 시간과 평행인 편광성분이 통과하는 데 걸리는 시간의 차이로 나타낼 수 있다. 이 시간 차이는 Kerr cell의 두께 L과 수직인 편광성분의 굴절각에 의해 결정되므로, 위상차이 P는 L과 K, E에 비례하며, 수직인 편광성분의 파장에 반비례한다. 따라서, 위상차이 P는 "
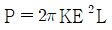 "와 같이 표현된다.
"와 같이 표현된다.






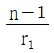
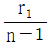
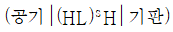
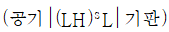
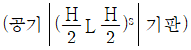
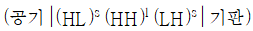
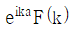
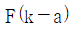
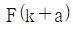
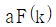
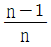
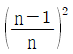
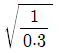
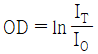
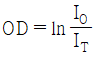
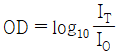
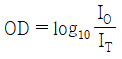
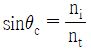
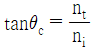
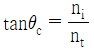
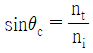
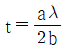
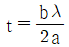
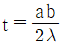
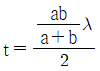
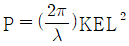
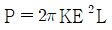
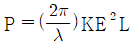
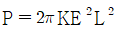
광선수차는 광이 렌즈를 통과할 때 굴절되는 정도에 따라 결정되는데, 이 굴절은 렌즈의 곡률과 빛의 파장에 따라 달라진다. 따라서 광선수차의 크기는 렌즈의 형태와 빛의 특성에 따라 달라지며, 광축에서 떨어진 높이 h와는 직접적인 관련이 없다. 따라서 h와 광선수차의 크기는 비례하지 않는다.