1과목: 과목 구분 없음
1. A, B 두 대의 직류발전기가 병렬운전 조건을 만족하며 운전하여 총 100 [A]의 부하전류를 공급하고 있다. 직류발전기 A의 유기기전력은 113.2 [V]이고 내부저항은 0.12 [Ω]이며, 직류발전기 B의 유기기전력은 110 [V]이고 내부저항은 0.1 [Ω]이다. 직류 발전기 A의 분담전류[A]는?
- 30
- 40
- 60
- 70
2. 3상 전원의 수전단에서 전압 3,300 [V], 전류 1,000 [A], 뒤진 역률 0.8의 전력을 받고 있을 때 동기조상기로 역률을 개선하여 1로 하고자 한다. 필요한 동기조상기의 용량[kVA]은?
- 약 315
- 약 350
- 약 3,150
- 약 3,500
3. 3,300 / 220 [V], 10 [kVA]의 단상변압기의 임피던스전압은 66 [V]이고 임피던스와트는 100 [W]이다. 이 변압기에 정격전류가 흐르는 경우 전압 변동률이 최대로 되는 부하역률[%]은?
- 50
- 58
- 71
- 87
4. 정지 시 2차 1상의 전압이 220 [V]이고 4극, 60 [Hz]인 유도 전동기가 1,260 [rpm]으로 회전할 경우 2차 전압 [V]과 슬립 주파수[Hz]는? (순서대로 2차 전압, 슬립주파수)
- 22, 6
- 44, 12
- 66, 18
- 110, 30
5. 3상 200 [V]의 교류전원을 6개의 역저지 3단자 사이리스터에 의해 구성되는 브릿지 회로로 정류 시 제어각 α를 π/3[rad]로 할 때, 직류측의 평균전압[V]은? (단, 직류측의 전류는 연속이고, 교류측의 임피던스는 무시한다)
- 105
- 120
- 135
- 150
6. 어떤 타여자 직류발전기가 800 [rpm]으로 회전할 때 120 [V]의 기전력을 유도하는데 4 [A]의 여자전류를 필요로 한다. 이 발전기를 640 [rpm]으로 회전하여 140 [V]의 유도기전력을 얻으려 할 때 필요한 여자전류[A]는? (단, 자기회로의 포화현상은 무시한다)
- 35/6
- 6/35
- 14/3
- 3/14
7. 정격전압 6,000 [V], 정격용량 3,000√3[kVA], 정격주파수 60 [Hz]의 Y결선 3상 동기발전기가 있다. 여자전류 300 [A]에서 무부하 단자전압은 6,000 [V]이고 단락전류는 600 [A]일 때 이 발전기의 단락비는?
- 0.83
- 1.0
- 1.2
- 1.25
8. 60 [kVA], 4,000/200 [V]인 단상 변압기의 % 임피던스 강하가 2 [%]일 때 1차 단락전류[A]는?
- 825
- 750
- 650
- 625
9. 3상 유도전동기 출력이 P0, 2차 동손이 Pc2일 때의 슬립 s는? (단, 기계손은 무시한다)
10. 아래 그림은 크레인에서 일정한 속도로 하중을 감아 내리는 것을 표현하고 있다. 이 상황에서 회생제동으로 전력을 회수 하려고 한다. 부하 하중의 중량이 612[kg]이고 전동기의 감아서 내리는 속도가 10 [m/min]일 때 회생제동으로 회수되는 전력[kW]은? (단, 권상장치의 효율은 100 [%]이다)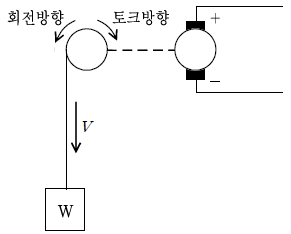
- 약 1
- 약 6.12
- 약 10
- 약 61.2
11. 직류 분권전동기의 계자전류를 정격값으로 일정하게 유지하고 정격속도의 1.2배의 속도로 정격토크의 1.2배의 토크를 발생하도록 하는 데 필요한 전력은? (단, 전기자 저항강하 및 전기자반작용은 무시한다)
- 정격전력
- 정격전력의 1.2배
- 정격전력의 1.44배
- 정격전력의 2.4배
12. 정격이 400 [VA]인 단상변압기의 철손이 6[W], 전부하 동손이 24[W]이다. 효율이 최대가 되기 위한 부하[VA]는?
- 100
- 200
- 300
- 400/√2
13. 정격출력 15 [kW], 단자전압 220 [V], 4극, 60 [Hz]인 3상 유도 전동기가 정격부하에서 1,728 [rpm]으로 회전한다. 2차 저항을 2.5배로 증가 시키면 같은 부하 토크에서 회전수[rpm]는?
- 1,530
- 1,620
- 1,710
- 1,728
14. 아래 그림과 같은 승압형 직류 초퍼가 부하저항 2 [Ω], 커패시터 0.01 [F] 일 때, 커패시터 전압의 맥동을 4 [%] 이내로 하기 위한 최소 스위칭 주파수[Hz]는? (단, 듀티비는 0.4이다)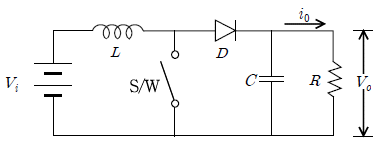
- 1,250
- 750
- 625
- 500
15. 단자전압 220 [V], 부하전류 46 [A], 계자전류 4 [A]인 직류 분권 발전기의 유기기전력이 240 [V]이다. 전기자 저항[Ω]은?
- 2.5
- 2.3
- 0.43
- 0.4
16. 병렬운전중인 2대의 동기발전기의 대응하는 기전력 상호간에 60°의 위상차가 있을 때 두 발전기 사이의 동기화력[kW/rad]은? (단, 각 발전기의 상전압 3,000 [V], 동기리액턴스 5 [Ω]이고, 전기자 저항은 무시한다)
- 260
- 450
- 600
- 780
17. 1차전압이 3,000 [V], 권수비 20인 단상변압기가 전등부하에 10 [A]의 전류를 공급할 때 입력[kW]은? (단, 변압기는 이상 변압기이다)
- 0.5
- 1.0
- 1.5
- 2.0
18. 4극, 60 [Hz] 3상 유도전동기의 전전압 기동토크가 전부하 토크의 1.6배이다. 전전압의 1/√2배의 전압으로 기동하면 기동토크는 전부하 토크의 몇 배인가?
- 0.8배
- 1.6/√2배
- 1.6√2배
- 3.2배
19. 명판에 기재된 사양이 31.4 [kW], 300 [V], 1,200 [rpm]인 타여자 직류전동기가 있다. 이 전동기의 정격토크[Nㆍm]는? (단, π는 3.14로 계산한다)
- 250
- 260
- 270
- 280
20. 아래 그림과 같은 벅 직류-직류 변환기는 전원전압 60 [V], 주파수 24 [kHz], 듀티비 0.4, 인덕터 600[μH], 캐퍼시터 100[㎌], 저항 24[Ω]의 파라미터로 구성되어 있다. 소자들이 이상적이라고 가정하면 인덕터 전류의 최대값 [A]은?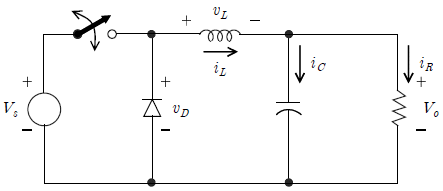
- 1.0
- 1.5
- 2.0
- 2.5






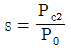
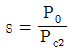
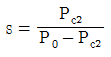
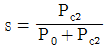
전체 회로의 내부저항 R = 0.12Ω + 0.1Ω = 0.22Ω
전압은 두 발전기의 유기기전력이므로 113.2V와 110V이다.
전류는 총 100A이므로, 오므로 오름차순으로 두 발전기의 분담전류를 x, y라고 하면 다음과 같은 방정식이 성립한다.
x + y = 100
113.2x / (0.12 + R) = 110y / (0.1 + R)
위의 방정식을 풀면 x = 60 이므로, 직류 발전기 A의 분담전류는 60A이다.