1과목: 과목 구분 없음
1. 콘크리트의 설계기준강도(fck)가 25MPa일 때 보통 골재를 사용한 콘크리트(ωc=2300kg/m3)의 탄성계수(Ec)[MPa]는?
- 2.05 × 104
- 2.35 × 104
- 2.65 × 104
- 2.95 × 104
2. 휨모멘트(M) 1650 kNㆍm(자중포함)가 작용하는 PSC보에 프리스 트레스힘(P) 3300 kN이 가해졌을 때 내력모멘트의 팔길이[m]는?
- 0.4
- 0.5
- 0.2
- 0.3
3. 폭 b=300 mm, 유효깊이 d=550mm, 인장철근 AS=2040mm2인 단철근 직사각형단면의 공칭 휨모멘트강도[kNㆍm]는? (단, fck=30MPa, fy=300MPa)
- 26
- 30.6
- 260
- 306
4. 강도설계법으로 설계 시 fck=30MPa, fy=300MPa인 단철근 직사각형보의 균형철근비는? (단, β1= 0.84)
- 0.0176
- 0.0276
- 0.0376
- 0.0476
5. 그림과 같은 직사각형보에서 fck=30MPa, fy=300MPa, a=150mm일 때, 콘크리트가 부담하는 압축력[kN]은?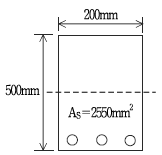
- 565
- 665
- 765
- 865
6. 프리스트레스힘에 대한 설명으로 옳지 않은 것은?
- 일반적으로 프리스트레스힘에 의해 보의 변형이 구속되어 부정 정력이 발생하게 되는데, 단면의 응력을 검토할 경우에는 이 부정정력을 고려하여야 한다.
- 유효프리스트레스힘은 프리스트레싱 직후 프리스트레스힘의 감소, 콘크리트의 크리프, 콘크리트의 건조수축, PS강재의 릴랙세이션 등의 영향을 고려하여 산출된다.
- 프리스트레싱 직후 프리스트레스힘의 손실량을 추정할 때 포스트텐션 방식에서는 콘크리트의 탄성변형만을 고려하여야 하고, 프리텐션 방식에서는 콘크리트의 탄성변형, PS강재와 쉬스의 마찰, 정착장치에서의 활동을 고려하여 검토하여야 한다.
- 설계 시 고려하여야 할 주요 프리스트레스힘에는 프리스트레싱 직후의 프리스트레스힘과 유효프리스트레스힘 등이 있다.
7. 길이(ℓ)가 6m이고 직사각형 단면(유효깊이 d=400mm)의 철근 콘크리트 단순보에 계수분포하중(ωu) 32kN/m가 작용하고 있다. 강도설계법으로 설계 시 이 단면의 콘크리트가 부담하는 공칭 전단강도 (Vc)가 70 kN인 경우, 전단철근이 부담해야 하는 공칭 전단강도(Vs)의 최소값[kN]은?
- 22
- 28
- 34
- 40
8. 지름이 800mm인 철근콘크리트 원형단면 비횡구속 골조의 기둥 양단이 고정되어 있는 경우, 단주로 볼 수 있는 기둥의 최대 높이 [m]는? (단, k=1.1)
- 4
- 5
- 6
- 7
9. 나선철근 기둥의 심부지름이 300mm이고, 기둥단면의 지름이 400 mm인 기둥의 최소 나선철근비는? (단, fck=30MPa, fy=fy=300MPa)
- 0.020
- 0.025
- 0.030
- 0.035
10. 프리스트레싱 긴장재의 허용응력규정에 관한 설명 중 가장 적당 한 것은? (여기서, fpu는 프리스트레싱 긴장재의 설계기준 인장 강도이고, fpy 프리스트레싱 긴장재의 설계기준 항복강도이다)
- 긴장을 할 때 프리스트레싱 긴장재의 인장응력은 0.80fpu 또는 0.94fpy중 큰 값 이상으로 하여야 한다.
- 긴장을 할 때 프리스트레싱 긴장재의 인장응력은 0.80fpu 또는 0.94fpy중 작은 값 이하로 하여야 한다.
- 긴장을 할 때 프리스트레싱 긴장재의 인장응력은 0.74fpu 또는 0.82fpy중 큰 값 이상으로 하여야 한다.
- 긴장을 할 때 프리스트레싱 긴장재의 인장응력은 0.74fpu 또는 0.82fpy중 작은 값 이하로 하여야 한다.
11. 축력과 휨모멘트를 받는 기둥의 축력-휨모멘트 상관도를 그림과 같이 A, B, C, D 4개의 영역으로 구분하였다. 어떤 영역에 포함 되도록 기둥을 설계하는 것이 가장 바람직한가?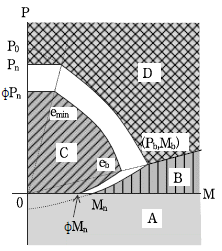
- A
- B
- C
- D
12. 단면적이 400mm2이고, 길이가 10m인 강봉(steel bar)이 온도변화의 영향으로 3mm가 늘어났다. 이 인장변형을 억제하는 데 필요한 최소 압축력[kN]은? (단, 강봉의 탄성계수 Es=2.1×105MPa)
- 25.2
- 30.2
- 35.2
- 37.2
13. 비틀림을 받는 부재를 보강하기 위하여 사용하는 종방향 철근 또는 종방향 긴장재와 함께 사용하는 횡방향 철근으로 적당하지 않은 것은?
- 부재축에 수직인 폐쇄스터럽 또는 폐쇄띠철근
- 부재축에 수직인 횡방향 강선으로 구성된 폐쇄용접철망
- 프리스트레싱되지 않은 부재에서 나선철근
- 두 개의 U형 스터럽을 거꾸로 겹쳐서 만든 철근
14. 다음 그림과 같이 등분포하중을 받고 있는 철근콘크리트보의 중립축에 있는 미소요소에 대한 설명으로 옳지 않은 것은?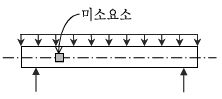
- 콘크리트의 휨 응력은 0이다.
- 단면에서의 전단응력이 최대가 된다.
- 휨변형과 전단변형이 일어난다.
- 사인장균열이 발생한다.
15. 그림과 같이 경간(L) 12 m인 연속 T형보에서 비대칭 부분의 플랜지 유효폭[mm]은?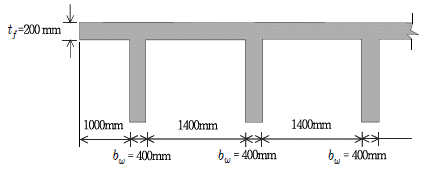
- 1000
- 1100
- 1400
- 1600
16. 인장력 600 kN이 작용하는 두께 20mm의 강판(SS400)을 지압이 음용 고장력볼트(M22-B8T)를 사용하여 2면전단으로 연결할 때 필요한 최소 볼트수는? (단, 1면 전단에 대한 볼트 1개당 허용 전단력 Pva=55 kN, 볼트 1개당 허용지압력 Pba=105 kN)
- 3
- 4
- 5
- 6
17. 그림과 같이 3.5m× 1.6m인 독립확대기초에서 사하중 500 kN이 500mm× 500mm의 기둥에 작용한다. 이 독립확대기초에서 1방향 배근 시 전단력에 대한 위험단면의 위치를 나타내는 거리(c)[m]는? (단, 유효높이(d)는 450mm이다)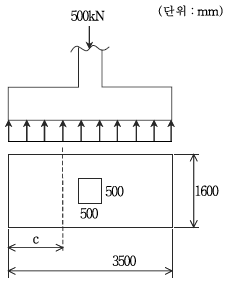
- 1.00
- 1.05
- 1.10
- 1.15
18. 콘크리트 구조설계기준(2003년도 개정)에서 비틀림 설계에 관한 사항 중 옳지 않은 것은?
- 콘크리트의 전단과 비틀림 강도의 상호 작용을 고려해야 한다.
- 콘크리트의 전단강도는 비틀림과 상관없이 일정하다.
- 비틀림에 대한 설계는 박벽관(thin-walled tube)과 입체트러스 해석법에 근거를 두고 있다.
- 비틀림 설계시 보 단면에서 가운데 부분의 콘크리트는 무시한다.
19. 콘크리트의 재료 특성에 관한 설명으로 옳지 않은 것은?
- 콘크리트의 크리프는 물시멘트비, 시멘트량 및 수화율이 감소할수록 감소한다.
- 콘크리트의 크리프는 재령보다 해당 재령에서의 수화율에 따라 더 큰 영향을 받는다.
- 온도가 상승함에 따라 수축에 미치는 영향은 온도가 올라가기 전에 콘크리트의 함수상태, 온도증가 후의 수분손실 등에 따라 크게 변화한다.
- 콘크리트의 건조수축은 물시멘트비와 시멘트량이 감소할수록 수축도 감소한다.
20. 암거 설계에 대한 설명으로 옳지 않은 것은?
- 암거의 단면은 배수 유량이나 구배에 따라 결정되지만, 단면 치수나 철근량은 매설깊이에서의 하중을 고려하여 결정된다.
- 암거의 설계 유량은 안전을 위하여 평균 유량의 2배를 가정하며 이것을 하중으로 고려한다.
- 슬래브식 상자형 암거(box culvert)의 경우 양측벽을 옹벽으로 생각하여 상부 슬래브를 단순보로 고려한다.
- 암거의 폭에 비하여 길이가 충분히 길고, 흙의 두께가 일정한 경우에는 종단방향의 부재력 변화를 고려하지 않고, 횡단방향의 부재력을 고려한다.






하지만 이 문제에서는 골재를 사용한 콘크리트라는 조건이 주어졌습니다. 골재를 첨가함으로써 콘크리트의 탄성계수는 증가하게 됩니다. 이 때, 골재의 첨가비율인 첨가율(ωc)이 증가할수록 탄성계수는 증가하게 됩니다.
보기에서는 첨가율이 2300kg/m3로 주어졌으므로, 탄성계수는 7.5 × (1 + 0.04ωc)로 계산됩니다. 따라서,
7.5 × (1 + 0.04 × 2300) = 2.35 × 104
이 됩니다. 따라서 정답은 "2.35 × 104"입니다.