1과목: 과목 구분 없음
1. 배합설계 과정에서 단위수량 180kg, 단위시멘트량 315kg, 공기량 5%가 결정되었다면 골재의 절대용적[ℓ]은? (단, 시멘트 밀도는 0.00315g/㎣이고, 혼화재는 사용하지 않는다)
- 530
- 600
- 670
- 740
2. 폭 b=300 mm, 유효깊이 d=500 mm인 단철근 직사각형 철근 콘크리트 보의 단면이 균형변형률 상태에 있을 때, 압축연단에서 중립축까지의 거리 c[mm]는? (단, 콘크리트의 설계기준압축강도 fck=24MPa, 철근의 설계기준항복강도 fy=400MPa이며, 설계코드(KDS: 2016)와 2012년도 콘크리트구조기준을 적용한다)
- 250
- 275
- 300
- 330
3. 그림과 같이 긴장재를 포물선 모양으로 배치한 PSC 단순보의 하중평형 개념에 의한 부재 중앙에서 휨모멘트[kNㆍm]는? (단, 자중을 포함한 등분포하중 w=10 kN/m이며, 손실이 모두 발생한 후의 긴장력은 1,200 kN이다)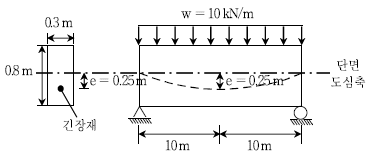
- 100
- 200
- 240
- 300
4. 중심축하중을 받는 길이 L =10 m, 직사각형 단면의 크기 0.1m × 0.12 m이고 양단 힌지인 기둥의 좌굴 임계하중 Pcr[kN]은? (단, π=3으로 계산하며 기둥의 탄성계수 E =20 GPa이고, 기둥 내의 응력이 비례한도 이하이다)
- 9
- 18
- 72
- 103.7
5. 기초판의 최대 계수휨모멘트를 계산할 때, 그 위험단면에 대한 설명으로 옳지 않은 것은? (단, 설계코드(KDS: 2016)와 2012년도 콘크리트구조기준을 적용한다)
- 강재 밑판을 갖는 기둥을 지지하는 기초판은 기둥 외측면과 강재 밑판 단부의 중간
- 콘크리트 기둥, 주각 또는 벽체를 지지하는 기초판은 기둥, 주각 또는 벽체의 외면
- 조적조 벽체를 지지하는 기초판은 벽체 중심과 단부의 중간
- 다각형 콘크리트 기둥은 같은 면적 원형 환산단면의 외면
6. 직접설계법에 의한 2방향슬래브의 내부 경간 설계에서 전체 정적계수모멘트(M0)가 300 kNㆍm일 때, 부계수휨모멘트[kNㆍm는? (단, 설계코드(KDS: 2016)와 2012년도 콘크리트구조기준을 적용한다)
- 105
- 150
- 195
- 240
7. 다음과 같은 수직 전단철근배치 범위에 대한 그래프에서 전단철근량 Av 및 전단철근 전단강도 Vs의 한계치를 옳게 표시한 것은? (단, Av: 전단철근의 단면적, Vs: 전단철근에 의한 단면의 공칭 전단강도, Vc: 콘크리트에 의한 단면의 공칭전단강도, Vu: 단면에서의 계수전단력, fck: 콘크리트의 설계기준압축강도, fyt: 전단 철근의 설계기준항복강도, bω: 복부의 폭, d: 단면의 유효깊이, s: 전단철근의 간격, ø : 전단에 대한 강도감소계수, 설계코드 (KDS: 2016)와 2012년도 콘크리트구조기준을 적용한다)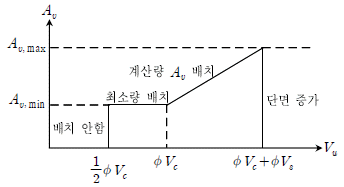
8. 그림과 같이 장방형 무근 콘크리트보에서 3등분점 하중법(KS F2408)에 의해서 보가 파괴될 때까지 시험을 실시하였다. 하중 P가 100 kN에서 시편의 지간 중앙이 파괴되었을 때의 최대인장응력 [MPa]은? (단, 거동이 탄성적이고 휨응력이 단면의 중립축에서 직선으로 분포한다고 가정한다)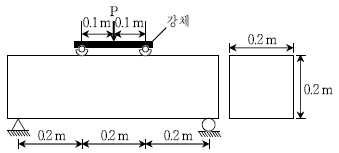
- 7.5
- 10.0
- 12.5
- 25.0
9. 그림과 같은 복철근 직사각형 보에서 인장철근과 압축철근이 모두 항복할 때, 등가직사각형 응력블록의 깊이 a[mm]는? (단, 인장 철근량 As=4,050mm2, 압축철근량 A′s=1,500mm2, 콘크리트의설계기준압축강도 fck=30MPa, 철근의 설계기준항복강도 fy=300MPa이고, 설계코드(KDS: 2016)와 2012년도 콘크리트 구조기준을 적용한다)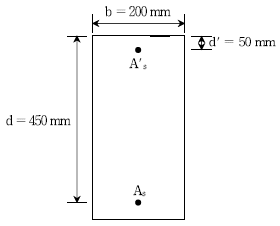
- 125
- 150
- 175
- 200
10. 축방향 인장을 받는 부재 및 이음재의 설계에 대한 설명으로 옳지 않은 것은? (단, 설계코드(KDS: 2016)와 도로교설계기준(한계상태설계법) 2015를 적용한다)
- 축방향 인장을 받는 부재의 강도는 전단면 파단을 고려하여 결정한다.
- 인장부재는 세장비 규정과 피로에 관한 규정을 만족해야 하며, 연결부 끝부분에서 블록전단강도에 관한 검토를 해야 한다.
- 축방향 인장력과 휨모멘트를 동시에 받아 순압축응력이 작용하는 플랜지는 국부좌굴에 대한 검토가 필요하다.
- 아이바, 봉강, 케이블 및 판을 제외한 인장부재에서 교번응력을 받지 않는 인장 주부재의 최대 세장비는 200이다.
11. 압축연단에서 압축철근까지의 거리 d'=50mm, 중립축까지의 거리 c=150mm인 복철근 철근콘크리트 직사각형보의 휨파괴 시 압축철근 변형률은? (단, 압축철근은 1단 배근되어 있고, 파괴 시 압축연단 콘크리트의 변형률은 0.003이고, 설계코드(KDS: 2016)와 2012년도 콘크리트구조기준을 적용한다)
- 0.0005
- 0.001
- 0.0015
- 0.002
12. H형강을 사용하여 길이가 4m이고 양단이 고정인 기둥을 설계할 때, 유효좌굴길이에 대한 세장비(λ)는? (단, H형강의 단면적은 1×103mm2이고, 강축의 단면2차모멘트는 1×107mm4, 약축의 단면2차모멘트는 6.4×106mm4이다)
- 20
- 25
- 40
- 50
13. 철근의 이음에 대한 설명으로 옳지 않은 것은? (단, 설계코드 (KDS: 2016)와 2012년도 콘크리트구조기준을 적용한다)
- 압축부에서 이음길이 조건을 만족하면, D41과 D51 철근은 D35이하 철근과의 겹침이음을 할 수 있다.
- 인장력을 받는 이형철근의 겹침이음길이는 A급과 B급으로 분류하며, 어느 경우에도 300mm 이상이어야 한다.
- 다발철근의 겹침이음에서 두 다발철근은 개개 철근처럼 겹침이음을 한다.
- 휨부재에서 서로 접촉되지 않게 겹침이음된 철근은 횡방향으로 소요 겹침이음길이의 1/5 또는 150 mm 중 작은 값 이상 떨어지지 않아야 한다.
14. 그림과 같은 2방향 확대기초에서 계수하중 Pu=1,000 kN이 작용할 때, 위험단면에 작용하는 계수전단력 Vu[kN]는? (단, 설계코드 (KDS: 2016)와 2012년도 콘크리트구조기준을 적용한다)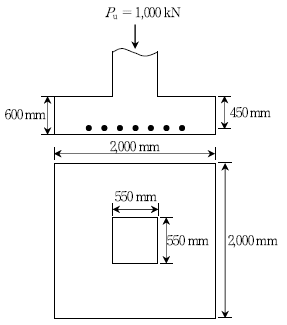
- 750
- 800
- 850
- 900
15. 보의 경간이 8m인 단순보에 등분포활하중이 20 kN/m, 자중을 포함한 등분포고정하중이 8 kN/m가 작용할 때, 휨부재를 설계하는 경우의 계수휨모멘트[kNㆍm]는? (단, KDS 24 12 11: 2016의 극한한계상태 하중조합 Ⅰ에 따라 활하중계수는 1.8, 고정하중계수는 1.25를 적용한다)
- 312.8
- 315.2
- 368.0
- 432.9
16. 그림과 같이 철근콘크리트 깊은 보를 스터럿-타이 모델에 의하여 설계할 때, 타이 BC에 필요한 휨 인장 철근면적[mm2]은? (단, 철근의 설계기준항복강도 fy=400MPa이고, 설계코드(KDS:2016)와 2012년도 콘크리트구조기준을 적용한다)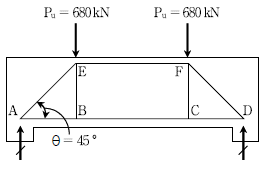
- 1,000
- 1,500
- 1,875
- 2,000
17. 양단 정착하는 PSC 포스트텐션 부재에서 일단 정착부 활동이 4mm 발생하였을 때, PS강재와 쉬스의 마찰이 없는 경우에 정착부 활동에 의한 프리스트레스 손실량[MPa]은? (단, PS강재의 길이 20m, 초기 프리스트레스 fi=1,200MPa, PS 강재 탄성계수 Eps=200GPa, 콘크리트 탄성계수 Ec=28GPa이다)
- 20
- 40
- 60
- 80
18. 연석간의 교폭이 9m, 발주자에 의해 정해진 계획차로의 폭이 9m일 때, 차량활하중의 재하를 위한 재하차로의 수 N은? (단, 설계코드 (KDS: 2016)와 도로교설계기준(한계상태설계법) 2015를 적용한다)
- 1
- 2
- 3
- 4
19. 그림과 같이 폭 0.36m, 높이 1 m인 직사각형 단면에 정모멘트가 3,000 kNㆍm, 긴장력이 3,600 kN이 작용하고 있다. 긴장재의 편심거리가 0.3m일 때, 응력개념에 의한 부재 상단응력의 크기 [MPa]는? (단, 구조물의 거동은 선형탄성으로 가정한다)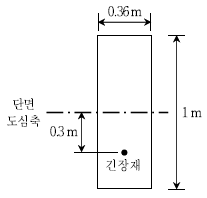
- 22
- 32
- 42
- 52
20. 그림과 같은 인장재 L형강의 순단면적[mm2]은? (단, 구멍의 직경은 25mm이고, 설계코드(KDS: 2016)와 도로교설계기준 (한계상태설계법) 2015를 적용한다)
- 1,344
- 1,444
- 1,544
- 1,750






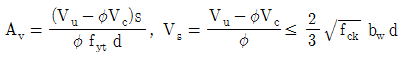

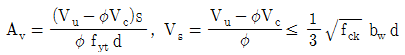
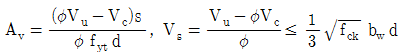
시멘트 315 : 골재 x : 공기 15.75
이때, 시멘트의 무게는 315kg이므로, 골재와 공기의 무게는 각각 다음과 같다.
골재의 무게 = 315kg * x / (315kg + 골재의 무게 + 15.75kg)
공기의 무게 = 315kg * 0.05x / (315kg + 골재의 무게 + 15.75kg)
또한, 단위수량 180kg에 대해 골재의 무게는 x이므로, 골재의 부피는 다음과 같다.
골재의 부피 = x * 180kg / 골재의 무게
시멘트의 밀도가 0.00315g/㎣이므로, 시멘트의 부피는 다음과 같다.
시멘트의 부피 = 315kg / 0.00315g/㎣ = 100000㎤
따라서, 전체 배합의 부피는 다음과 같다.
전체 배합의 부피 = 골재의 부피 + 시멘트의 부피 + 공기의 부피
= x * 180kg / 골재의 무게 + 100000㎤ * 0.05x / (315kg + 골재의 무게 + 15.75kg) + 100000㎤
이때, 전체 배합의 부피는 단위수량 180kg에 대한 것이므로, 전체 배합의 부피를 180kg으로 나누어 단위수량 1에 대한 부피를 구한다.
단위수량 1에 대한 부피 = (x * 180kg / 골재의 무게 + 100000㎤ * 0.05x / (315kg + 골재의 무게 + 15.75kg) + 100000㎤) / 180kg
이 값을 골재의 절대용적[ℓ]으로 변환하면 된다. 골재의 밀도는 일반적으로 2.6g/㎤ 정도이므로, 골재의 부피를 1000으로 나누어 리터 단위로 변환한다.
골재의 절대용적[ℓ] = (x * 180kg / 골재의 무게 + 100000㎤ * 0.05x / (315kg + 골재의 무게 + 15.75kg) + 100000㎤) / 180kg * 골재의 밀도 / 1000
이 값을 계산하면, 골재의 절대용적[ℓ]은 약 670이 된다. 따라서, 정답은 "670"이다.