1과목: 과목 구분 없음
1. 콘크리트의 건조수축에 대한 설명으로 옳은 것은?
- 습윤양생하에서 건조수축량은 증가한다.
- 물-시멘트비가 클수록 건조수축량은 감소한다.
- 대기 중의 습도가 증가하면 건조수축량은 감소한다.
- 콘크리트 타설 시 다짐을 잘하면 건조수축량은 증가한다.
2. 콘크리트의 압축강도에 대한 설명으로 옳지 않은 것은?
- 골재의 강도가 커질수록 콘크리트의 압축강도는 증가한다.
- 물-시멘트비가 작을수록 콘크리트의 압축강도는 증가한다.
- 콘크리트를 건조양생하면 습윤양생에 비해 압축강도가 더 증가한다.
- 콘크리트의 압축강도는 전이영역(transition zone)의 강도와 밀접한 관련이 있다.
3. 그림과 같은 직사각형 철근콘크리트 단면의 공칭휨강도 Mn[kN·m]은? (단, 콘크리트의 설계기준압축강도 fck=20MPa, 철근의 항복강도 fy=300MPa, As=1,700mm2이고, KDS 14 20 20 : 2022를 따른다.)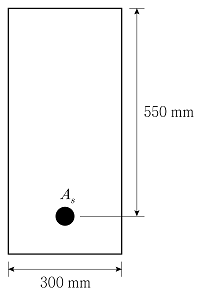
- 200
- 255
- 295
- 315
4. 슬래브와 보를 일체로 친 대칭 T형보의 플랜지 유효폭을 결정하는 기준에 해당하지 않는 것은? (단, tf=플랜지의 두께, bω=복부의 폭, KDS 14 20 10 : 2021을 따른다.)
- 8bω
- 16tf+bω
- 보의 경간의 1/4
- 양쪽 슬래브의 중심 간 거리
5. 복철근 직사각형보에서 압축철근을 배근하는 이유로 옳지 않은 것은?
- 전단철근 등 철근의 조립이 편리하다.
- 파괴 시 중립축의 깊이가 감소하며 부재의 연성이 증가한다.
- 인장철근의 변형률 증가를 억제함으로써 탄성처짐을 감소시킨다.
- 지진하중과 같이 하중의 작용 방향이 달라질 경우에 압축철근이 인장철근의 역할을 할 수 있다.
6. 철근콘크리트 휨부재에서 철근의 항복강도 fy=500MPa일 때, 인장지배변형률의 한계값(㉠)과 최소허용인장변형률의 값(㉡)을 바르게 연결한 것은? (단, KDS 14 20 20 : 2022를 따른다.)
- ①
- ②
- ③
- ④
7. 그림과 같이 휨모멘트를 받는 복철근 직사각형보의 콘크리트 압축연단이 극한변형률에 도달할 때, 압축철근의 변형률 ɛs′에 대한 인장철근의 변형률 ɛs의 비[ɛs/ɛs′]는? (단, 콘크리트의 설계기준압축강도 fck=30MPa, 철근의 항복강도 fy=400MPa, As′=420mm2, As=4,500mm2이고, KDS 14 20 20 : 2022를 따른다.)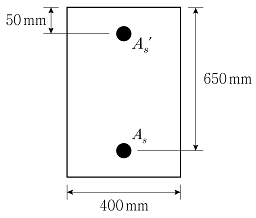
- 1.5
- 2.0
- 2.5
- 3.0
8. 철근의 정착에 대한 설명으로 옳지 않은 것은? (단, KDS 14 20 52 : 2022를 따른다.)
- 확대머리 이형철근은 경량콘크리트에 적용할 수 없다.
- 인장 이형철근의 정착길이는 공칭지름이 클수록 길어진다.
- 인장 이형철근의 표준 갈고리는 압축을 받는 경우 철근 정착에 유효하지 않은 것으로 본다.
- 동일한 철근과 콘크리트에 대해, 압축 이형철근이 인장 이형철근보다 더 큰 기본정착길이를 가진다.
9. 직사각형 철근콘크리트 단면의 계수전단력 Vu=350kN일 때, 수직 배근된 전단철근의 최대간격 s[mm]는? (단, 단면폭 b=400mm, 유효깊이 d=600mm, 보통중량 콘크리트를 사용하였고, 콘크리트의 설계기준압축강도 fck=25MPa, 전단철근의 항복강도 fy=400MPa, 전단철근의 단면적 Av=200mm2이며, KDS 14 20 22 : 2022를 따른다.)
- 120
- 180
- 240
- 300
10. 그림과 같이 사질토로 뒷채움된 철근콘크리트 옹벽의 A점에서의 전도 안전율은? (단, 흙의 내부마찰각 ø=30°, 흙의 단위중량 γ=18kN/m3, 철근콘크리트의 단위중량 mc=25kN/m3이다.)
- 2.0
- 2.5
- 3.0
- 3.5
11. 프리스트레스를 가하지 않은 나선철근 기둥의 최대 설계축강도 øPn(max)=øo×ø[0.85fck(Ag-Ast)+fyAst]에서 최소 편심에 대한 계수 øo의 값은? (단, Ast=축방향 철근량, Ag=기둥의 전체 단면적, fck=콘크리트의 설계기준압축강도, fy=철근의 항복강도, ø=강도감소계수이고, KDS 14 20 20 : 2022를 따른다.)
- 0.75
- 0.80
- 0.85
- 0.90
12. 구조용 강재의 장점으로 옳지 않은 것은?
- 내화성이 우수하다.
- 급속시공이 가능하다.
- 에너지 흡수능력이나 연성이 우수하다.
- 단위체적당 비강성 및 비강도가 매우 크기 때문에 대규모 구조물에 적합하다.
13. 프리스트레스의 시간적 손실 원인으로 옳지 않은 것은?
- 콘크리트의 크리프
- 콘크리트의 건조수축
- 긴장재 응력의 릴랙세이션
- 포스트텐션 긴장재와 덕트 사이의 마찰
14. 처짐을 계산하지 않는 경우, 단순지지된 리브가 없는 1방향 슬래브의 최소두께[mm]는? (단, 큰 처짐에 의해 손상되기 쉬운 칸막이벽이나 기타 구조물을 지지 또는 부착하지 않고, 부재의 길이 ℓ=8m, 보통중량 콘크리트와 설계기준항복강도 fy=400MPa 철근을 사용하며, KDS 14 20 30 : 2021을 따른다.)
- 286
- 333
- 400
- 500
15. 그림과 같이 맞댐용접을 한 두께 12mm의 강재판에 축방향 인장력 P=300kN이 작용할 때, 용접부에 발생하는 인장응력[MPa]은? (단, 용접 시점 및 종점부의 크레이터 영향은 무시하고, KDS 14 30 25 : 2019를 따른다.)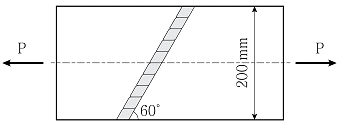
- 110
- 115
- 120
- 125
16. 프리스트레스트 콘크리트용 그라우트에 대한 설명으로 옳지 않은 것은? (단, KCS 14 20 53 : 2022를 따른다.)
- 그라우트의 물-결합재비는 45% 이하로 한다.
- 사용 혼화제는 블리딩 발생이 없는 타입을 표준으로 한다.
- 부재 콘크리트와 긴장재를 일체화시키는 부착강도는 재령 28일 인장강도로 설정할 수 있다.
- 부식성 물질의 함유로 인한 강재 부식이 구조물의 소요 성능에 손상을 일으키지 않도록 하여야 한다.
17. 그림과 같은 프리스트레스트 콘크리트 단순보의 지간 중앙에서 프리스트레스 힘 P=500kN에 의한 상향력과 평형을 이루는 등분포하중 ω[kN/m]는? (단, 자중과 프리스트레스 손실은 무시한다.)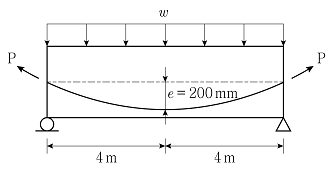
- 12.5
- 13.0
- 13.5
- 14.0
18. 계수전단력 Vu=50kN이 작용하는 직사각형 단면의 철근콘크리트 휨부재에서 전단철근을 배근하지 않아도 되는 단면의 최소폭[mm]은? (단, 보통중량 콘크리트를 사용하였고, 콘크리트의 설계기준압축강도 fck=25MPa, 단면의 유효깊이 d=500mm이며, KDS 14 20 22 : 2022를 따른다.)
- 160
- 320
- 380
- 480
19. 정사각형 독립기초의 상부기둥에 축방향으로 고정하중 D=1,000kN, 활하중 L=500kN이 작용하고 있으며, 기초의 자중이 300kN일 때, 독립기초 한 변의 최소길이[m]는? (단, 기초 밑면의 허용지지력 qa=200kN/m2이다.)
- 2.4
- 3.0
- 3.4
- 4.0
20. 중심 축하중만을 받는 철근콘크리트 단주의 역학적 거동에 대한 설명으로 옳지 않은 것은?
- 띠철근 기둥은 나선철근 기둥에 비해 횡구속이 크지 않다.
- 나선철근 기둥은 지진구역과 같이 연성의 증가가 필요한 곳에 주로 사용된다.
- 나선철근 기둥의 나선철근량이 작고, 간격이 크면 취성파괴가 일어날 수도 있다.
- 띠철근 기둥은 심부(core)콘크리트 파괴, 피복 콘크리트 탈락, 주철근 좌굴 순으로 파괴된다.





