1과목: 과목 구분 없음
1. 다음은 자료 x1, x2,···, xn에 대한 표본평균(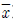 )의 성질이다. 이에 대한 설명으로 옳은 것만을 모두 고르면?
)의 성질이다. 이에 대한 설명으로 옳은 것만을 모두 고르면?
- ㄱ, ㄴ
- ㄱ, ㄷ
- ㄴ, ㄷ
- ㄱ, ㄴ, ㄷ
2.  일 때, P(A∩B)의 값은?
일 때, P(A∩B)의 값은?
- 1/12
- 1/6
- 1/4
- 1/3
3. 다음 상자그림(box plot)에 대한 설명으로 옳지 않은 것은?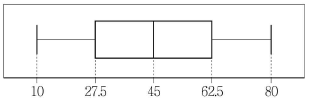
- 최솟값은 10이다.
- 범위(range)는 70이다.
- 45이상의 값을 갖는 자료는 전체 자료의 35%이다.
- 사분위수 범위는 35이다.
4. X1, X2, ···, Xn은 평균이 μ, 분산이 σ2인 확률표본(random sample) 이라고 하자. 표본평균 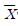 에 대한 설명 중 옳은 것만을 모두 고르면?
에 대한 설명 중 옳은 것만을 모두 고르면?
- ㄱ, ㄴ
- ㄱ, ㄷ
- ㄴ, ㄷ
- ㄱ, ㄴ, ㄷ
5. 세 확률변수 X1, X2, X3은 서로 독립이고, 각각의 확률분포는 다음과 같다. 변환된 확률변수 W=X1-2X2+X3에 대해 P(W>a)=0.05를 만족하는 실수 a의 값은? (단, za는 표준 정규분포의 제 100×(1-α) 백분위수이다)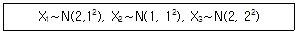
- 2+3×z0.05
- 2+3×z0.95
- 2+4×z0.05
- 2+4×z0.95
6. 어느 보험회사에서 도시 근로자의 평균 나이(μ)를 추정하기 위하여 64명을 임의로 추출하여 조사하였다. 64명 도시 근로자의 평균 나이가 36.38이고 표준편차가 11.07일 때, 모평균 μ에 대한 95%신뢰구간은? (단, 표준정규분포를 따르는 확률변수 Z에 대하여 P(Z≥1.96)=0.025, P(Z≥1.645)=0.05이다)
7. 다음은 정부의 미세먼지 관련 정책에 대한 남녀 간 지지도의 차이를 알아보기 위해서 남녀 각각 100명씩을 조사하여 얻은 결과표이다. 남성의 지지율(p1)보다 여성의 지지율(p2)이 더 큰지 유의수준 5%에서 검정할 때, Z검정통계량의 값(Z0)과 기각역을 옳게 짝지은 것은? (단, za는 표준정규분포의 제100×(1-α) 백분위수이다) (순서대로 Z검정통계량, 기각역)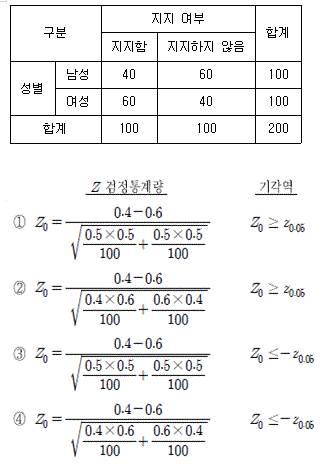
- ①
- ②
- ③
- ④
8. 두 확률변수 X, Y의 상관계수에 대한 설명으로 옳은 것만을 모두 고르면?
- ㄴ
- ㄱ, ㄴ
- ㄱ, ㄷ
- ㄴ, ㄷ
9. 다음은 카이제곱통계량을 이용하여 두 변수가 서로 독립인지 알아보기 위한 관측도수의 2×2 분할표이다. 카이제곱(X2) 검정에 대한 설명으로 옳지 않은 것은? (단, 귀무가설이 참일 때 각 셀의 기대도수는 5이상이고, 카이제곱통계량의 값은 k이다)
- 관측도수가 O11인 셀의 기대도수는
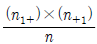 과 같다.
과 같다. - 관측도수가 O11인 셀의 기대도수와 O12인 셀의 기대도수의합은 n1+와 같다.
- X가 자유도 1인 카이제곱분포를 따를 때, 유의확률은 P(X≤k)와 같다.
- 전체 관측도수의 합과 전체 기대도수의 합은 같다.
10. F-분포에 대한 설명으로 옳은 것만을 모두 고르면? (단, Fα(k1, k2)는 분자의 자유도가 k1이고 분모의 자유도가 k2인 F-분포의 제 100×(1-α)백분위수이다)
- ㄱ, ㄴ
- ㄱ, ㄷ
- ㄴ, ㄷ
- ㄱ, ㄴ, ㄷ
11. 중심극한정리에 대한 설명으로 ㉠, ㉡에 들어갈 말을 옳게 짝지은 것은? (단, 모집단의 평균이 μ이고, 분산 σ2은 존재한다) (순서대로 ㉠, ㉡)
- 표본평균, 카이제곱분포
- 표본평균, 균등분포
- 표준화 표본평균, 지수분포
- 표준화 표본평균, 표준정규분포
12. 다음은 세 가지 속독법(A, B, C)에 따라 책 읽는 시간에 차이가 있는지 알아보기 위해 일원배치분산분석법을 적용하여 얻은 분산분석표이다. 각 속독법에 5명씩 15명을 임의로 배치하여 책을 읽게 한 후, 책 읽는 시간을 측정하였다. 이에 대한 설명으로 옳지 않은 것은?
- ㉠의 값은 3이다.
- ㉡의 값은 12이다.
- ㉢의 값은 64이다.
- 유의수준 1%에서 검정할 때, 세 가지 속독법에 따라 책 읽는 시간에 차이가 있다고 할 수 있다.
13. 다음은 입학 시 수학 성적(X)과 1학년 때의 통계학 성적(Y)에 대하여 단순선형회귀모형 Yi=α+βXi+εi, i = 1, 2, ···, n을 적용하여 얻은 결과이다. 이에 대한 설명으로 옳은 것은? (단, Fα(k1, k2)는 분자의 자유도가 k1이고 분모의 자유도가 k2인 F-분포의 제 100×(1-α) 백분위수를 나타내고, F0.05(1, 10)=4.96, F0.05(1, 11)=4.84 이다. 그리고 tα(k)는 자유도가 k인 t-분포의 제 100×(1-α) 백분위수를 나타내고, t0.05(10)=1.812, t0.025(10)=2.228, t0.025(11)=2.201이다)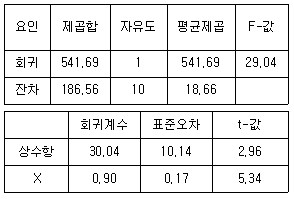
- 자료의 개수(n)는 11이다.
- 추정된 회귀직선은 Y=10.14+0.17X이다.
- X와 Y사이의 모상관계수(p)가 0인지 검정할 때, 귀무가설(H0:p=0)은 유의수준 5%에서 기각되지 않는다.
- 추정된 회귀모형의 유의성을 검정할 때, 귀무가설(H0:회귀모형은 유의하지 않다)은 유의수준 5%에서 기각된다.
14. 확률변수 X와 Y의 분산과 공분산은 다음과 같다. 확률변수 W와 T를 각각 W=2X+2, T=-Y+1이라고 할 때, W와 T의 상관계수는?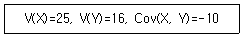
- -1/2
- 1/2
- -1
- 1
15. 확률변수 X는 N(μ, 1)를 따를때, 가설 H0: μ=μ0 대 H1:μ=μ1 대한 기각역이 R={x:x≥μ1+c}로 주어진 경우, 다음 그림에서 제 1종 오류를 범할 확률에 해당하는 영역(A)과 제 2종 오류를 범할 확률에 해당하는 영역(B)을 옳게 짝지은 것은? (단, μ1>μ0이고, c>0이다) (순서대로 A, B)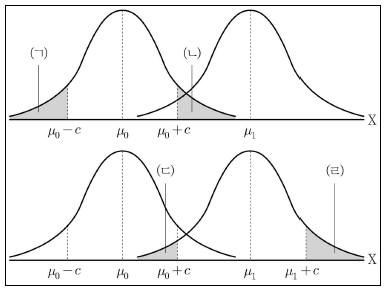
- ㄱ, ㄷ
- ㄱ, ㄹ
- ㄴ, ㄷ
- ㄴ, ㄹ
16. 다음은 다이어트 종류에 따라 체중 감량 효과에 차이가 있는지 알아보기 위해 분산분석을 시행한 결과표이다. 이 결과에서 알 수 있는 내용으로 옳지 않은 것은? (단, Fα(k1, k2)는 분자의 자유도가 k1이고, 분모의 자유도가 k2인 F-분포의 제 ?00×(1-α) 백분위수를 나타내고, F0.05(3, 26)=2.98, F0.025(3, 26)=3.67이다)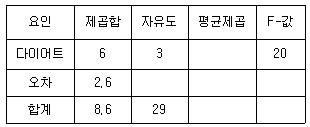
- 다이어트 종류는4가지이다.
- F-값은 오차의 평균제곱을 처리의 평균제곱으로 나눈 값이다.
- F-값과 분자의 자유도 3, 분모의 자유도가 26인 F-분포를 이용하여 유의확률(p-값)을 구할 수 있다.
- 유의수준 5%에서 다이어트 종류에 따라 체중 감량 효과에 차이가 있다고 할 수 있다.
17. 자료의 수가 n인 표본 (xi, yi)(i=1,2,···,n)에 대해 다음 두 회귀모형 M1과 M2를 적용하여 분석하고자 한다. 두 모형에 대한 설명으로 옳은 것만을 모두 고르면?
- ㄱ, ㄴ
- ㄱ, ㄷ
- ㄴ, ㄷ
- ㄱ, ㄴ, ㄷ
18. 어떤 자판기에서 판매되는 음료수 용량은 모평균이 μ(mL)이고, 모표준편차가 5mL인 확률분포를 따른다고 한다. 이 자동판매기에서 임의로 추출한 100개 음료수의 표본평균이 150mL일 때, 가설 H0:μ=μ0 대 H1:μ≠μ0에 대한 유의수준 α에서 귀무가설을 기각하지 못하는 μ0의 범위는? (단, zα는 표준정규분포의 100×(1-α) 백분위수이다)
19. 다음은 금연 프로그램에 참석한 120명을 대상으로 직업군에 따라 금연 성공률에 차이가 있는지 조사한 분할표이다. 이에 대한 설명으로 옳은 것은? (단, Oij(i=1,2,3,4, j=1,2) (i, j) 셀에서 얻어진 관측도수이고, Eij(i=1,2,3,4, j=1,2)는 귀무가설이 참일 때 (i, j)셀에서 얻어진 기대도수이다. 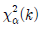 는 자유도가 k인 카이제곱분포의 제 100× (1-α) 백분위수이고, X2은 검정통계량이다)
는 자유도가 k인 카이제곱분포의 제 100× (1-α) 백분위수이고, X2은 검정통계량이다)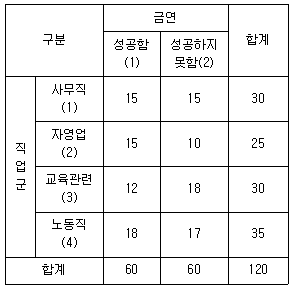
- 각 직업의 성공률을 pi(i=1,2,3,4)라고 할 때, 귀무가설은 H0:p1=p2=p3=p4=1/4이다.
- E11=15이다.
- 카이제곱 검정통계량은
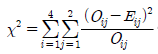 이다.
이다. - 유의수준 5%에서 검정할 때, 기각역은
 이다.
이다.
20. 다음 설명 중 옳은 것만을 모두 고르면?
- ㄱ
- ㄱ, ㄴ
- ㄴ, ㄷ
- ㄱ, ㄴ, ㄷ







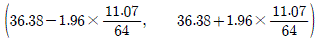

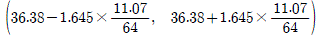
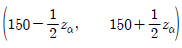
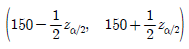

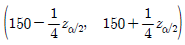
- 표본평균은 표본의 크기가 작을수록 모평균과의 차이가 커진다. (ㄷ)