9급 국가직 공무원 통계학개론 필기 기출문제복원 (2020-07-11)

9급 국가직 공무원 통계학개론 2020-07-11 필기 기출문제 해설

이 페이지는 9급 국가직 공무원 통계학개론 2020-07-11 기출문제를 CBT 방식으로 풀이하고 정답 및 회원들의 상세 해설을 확인할 수 있는 페이지입니다.

9급 국가직 공무원 통계학개론
(2020-07-11 기출문제)

목록

1과목: 과목 구분 없음

1. 다음 자료는 어느 고등학교 A, B반의 학생이 하루에 섭취하는 물의 양을 측정한 것이다. A반은 리터(L) 단위로 측정하고, B반은 밀리리터(mL) 단위로 측정하였다. A, B반 학생이 섭취하는 물의 양에 대한 산포를 비교하고자 할 때 가장 적합한 측도는?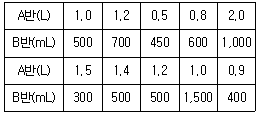

  1. 표준편차
  2. 사분위수 범위
  3. 제50백분위수
  4. 변동계수
(정답률: 66%)
  • 측정 단위가 서로 다른 두 집단(L와 mL)의 산포를 비교할 때는 절대적인 수치인 표준편차를 사용할 수 없습니다.
    단위의 영향을 제거하고 상대적인 산포도를 비교하기 위해서는 표준편차를 평균으로 나눈 값인 변동계수(Coefficient of Variation)를 사용하는 것이 가장 적합합니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

2. 두 사건 A, B에 대하여 P(A)=1/3, P(A|B)=1/9, P(A∩B)=1/12 일 때, 옳은 것만을 모두 고르면?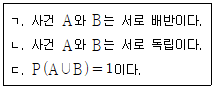

  1. ㄴ
  2. ㄷ
  3. ㄱ, ㄴ
  4. ㄴ, ㄷ
(정답률: 66%)
  • 조건부 확률과 독립, 배반 사건의 정의를 이용하여 판단합니다.
    1. $P(A \cap B) = 1/12 \neq 0$이므로 서로 배반이 아닙니다.
    2. $P(A|B) = 1/9$이고 $P(A) = 1/3$이므로 $P(A|B) \neq P(A)$ 입니다. 따라서 서로 독립이 아닙니다.
    3. $P(B) = \frac{P(A \cap B)}{P(A|B)} = \frac{1/12}{1/9} = \frac{9}{12} = 3/4$ 입니다.
    따라서 $P(A \cup B) = P(A) + P(B) - P(A \cap B) = 1/3 + 3/4 - 1/12 = 4/12 + 9/12 - 1/12 = 12/12 = 1$이 성립합니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

3. 다음 상자그림에 대한 설명으로 옳지 않은 것은?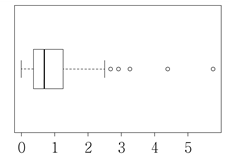

  1. 자료의 분포는 오른쪽으로 긴 꼬리를 가지는 비대칭 형태이다.
  2. 자료의 평균이 중앙값보다 작다.
  3. 자료의 중앙값은 1보다 작다.
  4. 자료의 왜도(skewness)는 정규분포의 왜도보다 크다.
(정답률: 71%)
  • 제시된 상자그림을 분석하면, 중앙값이 상자의 왼쪽에 치우쳐 있고 오른쪽으로 긴 꼬리와 이상치들이 분포하는 오른쪽 꼬리 분포(Positive Skew) 형태입니다.
    이런 비대칭 분포에서는 일반적으로 평균이 중앙값보다 크게 나타납니다. 따라서 자료의 평균이 중앙값보다 작다는 설명은 틀렸습니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

4. 두 확률변수의 상관계수에 대한 설명으로 옳지 않은 것은?

  1. 상관계수는 항상 -1과 1사이의 값이다.
  2. 공분산이 0이면 상관계수도 이다.
  3. 상관계수의 절댓값이 1에 가까울수록 두 확률변수는 강한 양의 상관관계가 있다.
  4. 상관계수는 두 확률변수의 선형 관계를 나타내는 측도이다.
(정답률: 57%)
  • 상관계수는 두 변수 사이의 선형적 관계의 강도를 나타내는 지표입니다.
    상관계수의 절댓값이 1에 가까울수록 선형 관계가 강한 것은 맞으나, 부호가 $+$이면 양의 상관관계, $-$이면 음의 상관관계라고 합니다. 따라서 절댓값이 1에 가깝다고 해서 무조건 양의 상관관계라고 할 수 없습니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

5. 어떤 전자부품의 불량률은 0.1이다. 전체 생산된 부품에서 임의로 추출된 100개의 부품 가운데 불량품의 개수를 확률변수 X라 할 때, 옳지 않은 것은?

  1. P(X=10) ＞ P(X=90)
  2. P(X≥1)=1
  3. X의 기댓값은 10이다.
  4. X의 표준편차는 3이다.
(정답률: 60%)
  • 이 문제는 이항분포 $B(n, p)$의 성질을 묻는 문제입니다. 시행 횟수 $n=100$, 성공 확률 $p=0.1$인 이항분포를 따릅니다.
    기댓값 $E(X) = np = 100 \times 0.1 = 10$이며, 분산 $V(X) = np(1-p) = 100 \times 0.1 \times 0.9 = 9$이므로 표준편차는 $\sqrt{9} = 3$입니다. 또한 $P(X=10)$은 확률 질량 함수에 의해 $P(X=90)$보다 훨씬 큽니다.

    오답 노트
    P(X≥1)=1: 모든 부품이 정상일 확률 $P(X=0) = 0.9^{100}$이 존재하므로, $P(X \ge 1) = 1 - P(X=0)$이 되어 1보다 작습니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

6. 두 확률변수 X, Y에 대한 설명으로 옳지 않은 것은?

  1. X+Y의 기댓값 E(X+Y)=E(X)+E(Y)이다.
  2. E(XY)=E(X)E(Y)이면 확률변수 X와 Y는 서로 독립이다.
  3. 확률변수 X와 Y가 서로 독립이면 두 확률변수의 차 X-Y의 분산 Var(X-Y)=Var(X)+Var(Y)이다.
  4. 확률변수 X와 Y가 서로 독립이면 두 확률변수의 공분산 Cov(X, Y)=0이다.
(정답률: 50%)
  • 두 확률변수가 독립이면 $E(XY) = E(X)E(Y)$가 성립하지만, 그 역인 $E(XY) = E(X)E(Y)$라고 해서 반드시 독립인 것은 아닙니다. 이는 두 변수가 '무상관'임을 의미할 뿐 '독립'을 보장하지는 않기 때문입니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

7. 모집단에서 크기가 16인 표본을 임의로 추출하여 구한 모평균의 95% 신뢰구간이 (20, 25)이다. 다음 설명 중 옳은 것만을 모두 고르면?

  1. ㄷ
  2. ㄱ, ㄴ
  3. ㄱ, ㄷ
  4. ㄱ, ㄴ, ㄷ
(정답률: 38%)
  • 신뢰구간의 정의에 따라 표본평균은 항상 신뢰구간의 정중앙에 위치하므로 표본평균이 구간 (20, 25) 안에 있다는 설명은 옳습니다.

    오답 노트
    모평균이 구간 안에 있을 확률: 신뢰구간은 표본을 뽑을 때마다 변하므로, 특정 구간에 모평균이 있을 확률을 0.95라고 말하는 것은 통계적으로 틀린 표현임
    표본의 95%가 구간 안에 있음: 신뢰구간은 모평균의 추정 범위이지 개별 표본 데이터의 분포 범위가 아님
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

8. 평균이 1이고, 분산이 4인 정규모집단에서 추출한 확률표본 X1, …, X9의 표본평균이 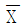이다. 실수 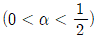에 대해 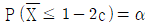를 만족시키는 c의 값은? (단, zα는 표준정규분포의 제 100×(1-α)백분위수이다)

  1. zα
  2. z1-α
(정답률: 29%)
  • 표본평균 $\bar{X}$의 분포는 정규분포 $N(\mu, \frac{\sigma^2}{n})$를 따르므로, 이를 표준화하여 $z_{\alpha}$와의 관계를 통해 $c$를 구합니다.
    ① [기본 공식] $P(\bar{X} \le \mu - z_{\alpha} \frac{\sigma}{\sqrt{n}}) = \alpha$
    ② [숫자 대입] $1 - 2c = 1 - z_{\alpha} \frac{2}{\sqrt{9}}$
    ③ [최종 결과] $c = \frac{1}{3} z_{\alpha}$
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

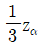
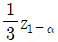
9. 어느 지역의 2019년 쌀 생산량을 추정하기 위해 이 지역 9개의 농지를 임의로 추출하여 단위면적당 쌀 생산량을 조사하였더니 표본평균 1,150kg, 표본표준편차 150kg이다. 이 지역의 2019년 단위면적당 평균 쌀 생산량이 2018년의 단위면적당 평균 쌀 생산량 1,100kg보다 크다는 주장을 검정하고자 한다. 귀무가설이 참일 때, t검정통계량의 값과 자유도 k를 옳게 짝 지은 것은? (단, 단위면적당 쌀 생산량은 정규분포를 따른다)(순서대로 t 검정통계량의 값, k)

  1. 1, 8
  2. 1, 9
  3. 1/3, 8
  4. 1/3, 9
(정답률: 54%)
  • 모표준편차를 모를 때 사용하는 t-검정통계량 공식과 자유도 공식을 적용합니다.
    ① [기본 공식]
    $$t = \frac{\bar{X} - \mu}{s / \sqrt{n}}, \quad k = n - 1$$
    ② [숫자 대입]
    $$t = \frac{1150 - 1100}{150 / \sqrt{9}}, \quad k = 9 - 1$$
    ③ [최종 결과]
    $$t = 1, \quad k = 8$$
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

10. 다음 중 서로 독립인 두 확률변수 X1, X2에 대해 옳은 것만을 모두 고르면? (단, ~는 확률변수가 해당 확률분포를 따르는 것을 나타낸다)

  1. ㄱ, ㄷ
  2. ㄱ, ㄴ, ㄹ
  3. ㄴ, ㄷ, ㄹ
  4. ㄱ, ㄴ, ㄷ, ㄹ
(정답률: 54%)
  • 독립인 확률변수들의 합과 차에 대한 분포의 재생성에 관한 문제입니다.
    ㄱ. 포아송분포의 합은 각 평균의 합을 평균으로 하는 포아송분포를 따릅니다.
    ㄴ. 카이제곱분포의 합은 각 자유도의 합을 자유도로 하는 카이제곱분포를 따릅니다.
    ㄷ. 성공확률 $p$가 같은 이항분포의 합은 시행횟수의 합을 시행횟수로 하는 이항분포를 따릅니다.
    ㄹ. 정규분포의 선형 결합은 정규분포를 따르며, 분산은 각각의 분산의 합으로 계산됩니다. 따라서 $X_{1} - X_{2} \sim N(\mu_{1} - \mu_{2}, \sigma^{2} + \sigma^{2}) = N(\mu_{1} - \mu_{2}, 2\sigma^{2})$가 성립합니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

11. 다음 귀무가설(H0)과 대립가설(H1)에 대한 검정법의 제2종 오류에 해당하는 것은?

  1. μ=10 일 때 귀무가설을 기각하는 것
  2. μ=15 일 때 귀무가설을 기각하는 것
  3. μ=10 일 때 귀무가설을 기각하지 않은 것
  4. μ=15 일 때 귀무가설을 기각하지 않은 것
(정답률: 58%)
  • 제2종 오류는 대립가설($H_{1}$)이 참임에도 불구하고 귀무가설($H_{0}$)을 기각하지 못하는 오류를 말합니다.
    제시된 가설에서 $H_{0}: \mu = 10$, $H_{1}: \mu \neq 10$이므로, 실제 $\mu$가 $10$이 아닌 상황($\mu = 15$)에서 귀무가설을 기각하지 않는 것이 제2종 오류에 해당합니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

12. 어떤 공무원이 종합민원실에 방문하는 민원인의 수가 요일별로 고르게 분포되어 있다고 생각한다. 이 가설을 확인하고자 4주간 요일별로 방문하는 민원인의 수를 정리하여 다음 표를 작성하였다.

이 가설의 검정방법에 대한 설명으로 옳지 않은 것은? (단, χ2α(k)는 자유도가 k인 카이제곱분포의 제 100×(1-α)백분위수를 나타낼 때 χ20.05(4)=9.49, χ20.05(5)=11.07이다)

  1. 귀무가설이 참일 때 민원인의 각 요일별 방확률은 0.2이다.
  2. 귀무가설이 참일 때 월요일에 방문하는 민원인의 수의 기대도수는 100이다.
  3. 이 가설을 검정하기 위한 카이제곱통계량의 값은 20이다.
  4. 유의수준 5%에서 요일별 방확률은 같다고 할 수 없다.
(정답률: 66%)
  • 요일별 방문객 수가 고르게 분포되어 있다는 가설은 적합도 검정(Goodness of Fit Test)을 통해 확인하며, 카이제곱 통계량을 사용합니다.
    전체 방문객 수 $500$명이 5개 요일에 고르게 분포한다면 기대도수는 각 요일별로 $500 \div 5 = 100$이며, 확률은 $1/5 = 0.2$입니다.
    카이제곱 통계량 계산 과정은 다음과 같습니다.
    ① [기본 공식] $\chi^{2} = \sum \frac{(O - E)^{2}}{E}$
    ② [숫자 대입] $\chi^{2} = \frac{(120-100)^{2}}{100} + \frac{(80-100)^{2}}{100} + \frac{(80-100)^{2}}{100} + \frac{(100-100)^{2}}{100} + \frac{(120-100)^{2}}{100}$
    ③ [최종 결과] $\chi^{2} = 4 + 4 + 4 + 0 + 4 = 16$
    따라서 통계량 값은 $16$이며, $20$이라는 설명은 틀렸습니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

13. 다음 분산분석에 대한 설명으로 옳은 것만을 모두 고르면?

  1. ㄱ, ㄷ
  2. ㄱ, ㄹ
  3. ㄴ, ㄷ
  4. ㄴ, ㄹ
(정답률: 48%)
  • 분산분석(ANOVA)은 여러 집단의 평균 차이를 검정하는 통계 기법입니다.
    ㄱ. 3개 이상의 모집단 평균 비교를 위한 기법이 맞습니다.
    ㄹ. 반복이 있는 이원배치법에서는 두 요인의 주효과뿐만 아니라 상호작용(교호작용)을 검정할 수 있습니다.

    오답 노트
    ㄴ. 각 모집단은 서로 동일한 분산을 가진다는 등분산성 가정이 필요합니다.
    ㄷ. 일원배치법에서 반복수가 일정하지 않아도 분석은 가능합니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

14. 키가 큰 사람의 연봉이 높다는 주장이 있다. 이를 검정하기 위해 MBA 졸업생 250명의 키(X)와 연봉(Y)을 조사하여 단순선형회귀분석한 결과의 일부가 다음 표와 같다. 키에 대한 회귀계수의 최소제곱추정량의 값 ㉠은? (단, 키에 대한 회귀계수는 양수이다)

  1. 0.8
  2. 1.0
  3. 2.0
  4. 4.0
(정답률: 34%)
  • 회귀계수의 최소제곱추정량은 $t$값의 정의인 $t = \frac{\text{계수}}{\text{표준오차}}$ 공식을 이용하여 구할 수 있습니다.
    ① [기본 공식] $\text{계수} = t \times \text{표준오차}$
    ② [숫자 대입] $\text{계수} = 4.0 \times 0.20$
    ③ [최종 결과] $\text{계수} = 0.8$
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

15. 두 인자 A와 B가 어떤 특성값에 영향을 주는가에 대해 인자의 수준 조합에서 동일하게 반복실험을 행하여 분산분석을 한 결과의 일부가 다음 표와 같다. 이에 대한 설명으로 옳지 않은 것은?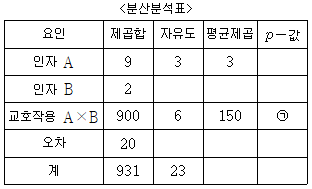

  1. 인자 A의 수준 수는 4이고, 인자 B의 수준 수는 3이다.
  2. 인자 A, B의 수준 조합에서 반드시 두 번의 반복실험을 해야 한다.
  3. 유의수준 5%에서 ㉠이 0.05보다 작으면 인자 A와 B의 각각에 대한 유의성 검정은 의미가 없다.
  4. 유의수준 5%에서 ㉠이 0.05보다 작으면 교호작용을 오차항에 풀링(pooling)하여 분산분석을 다시 실시한다.
(정답률: 21%)
  • 분산분석표에서 교호작용의 $p$-값이 유의수준 $0.05$보다 작다는 것은 교호작용이 통계적으로 유의하다는 것을 의미합니다. 교호작용이 유의할 때는 주효과(인자 A, B)를 개별적으로 해석하는 것이 무의미하며, 교호작용을 오차항에 풀링(pooling)해서는 안 됩니다. 풀링은 교호작용이 유의하지 않을 때(즉, $p$-값이 $0.05$보다 클 때) 수행합니다.

    오답 노트
    인자 A 수준 수: 자유도가 $3$이므로 수준 수는 $3+1=4$임
    인자 B 수준 수: 전체 자유도 $23$에서 A($3$), 교호작용($6$), 오차($23-3-6-2=12$)를 제외한 B의 자유도는 $2$이므로 수준 수는 $2+1=3$임
    반복실험 횟수: 오차 자유도 $12$를 수준 조합 수 $4 \times 3 = 12$로 나누면 반복 횟수 $n-1=1$이 되어 $n=2$회임
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

16. 흡연과 심근경색의 연관성을 평가하기 위하여 특정 병원을 방문하여 심근경색으로 진단된 환자 중에서 300명, 심근경색이 아닌 환자 중에서 600명을 각각 임의추출하여 흡연 여부를 조사한 분할표가 다음과 같다.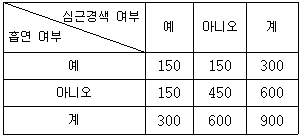

이 분할표에 대한 설명으로 옳은 것은?

  1. 동질성 검정의 카이제곱통계량의 자유도는 2이다.
  2. 동질성 검정의 카이제곱통계량의 값은 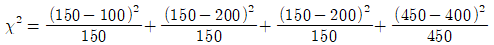이다.
  3. 분할표로부터 심근경색이 발병한 환자에서의 흡연율을 추정할 수 있다.
  4. 분할표로부터 흡연한 사람에서의 심근경색 발생률을 추정할 수 있다.
(정답률: 42%)
  • 이 문제는 환자-대조군 연구 설계로 추출된 분할표의 특성을 묻는 문제입니다. 심근경색 환자군($300$명)과 비환자군($600$명)을 각각 정해진 수만큼 추출했으므로, 심근경색 여부에 따른 흡연율(조건부 확률)은 계산 가능하지만, 전체 인구에서의 심근경색 발생률이나 흡연자 중 심근경색 발생률은 추정할 수 없습니다.

    오답 노트
    동질성 검정의 자유도: $(2-1) \times (2-1) = 1$이므로 틀림
    심근경색 발생률 추정: 표본 추출 단계에서 이미 환자/비환자 비율을 정했으므로 불가능함
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

17. 어떤 질병의 새로운 치료약을 개발하였다. 다음 표는 복용량에 따라 이 질병 증상의 경감기간을 알아보기 위해 명의 환자에 대하여 실험한 자료의 일부이다.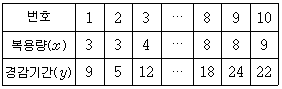

복용량과 경감기간의 관계를 단순선형회귀모형 yi=α+βxi+εi(i=1,2,…10)에 적용하였다. 이때 εi는 서로 독립이며 평균이 0, 분산이 σ2인 정규분포를 따른다. 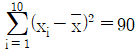, , 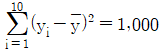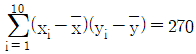일 때, 옳지 않은 것은? (단, 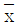, 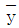는 각각 x, y의 표본평균이다)

  1. 회귀계수 β의 최소제곱추정량의 값은 3이다.
  2. 복용량과 경감기간의 상관계수는 0.9이다.
  3. 결정계수는 0.81이다.
  4. σ2의 불편추정량의 값은 190/9이다.
(정답률: 53%)
  • 단순선형회귀모형에서 회귀계수, 상관계수, 결정계수 및 오차분산의 불편추정량을 구하는 문제입니다.
    1. 회귀계수 $\beta$의 추정량: $\beta = \frac{\sum(x_i-\bar{x})(y_i-\bar{y})}{\sum(x_i-\bar{x})^2}$
    $$\beta = \frac{270}{90}$$
    $$\beta = 3$$
    2. 상관계수 $r$: $r = \frac{\sum(x_i-\bar{x})(y_i-\bar{y})}{\sqrt{\sum(x_i-\bar{x})^2 \sum(y_i-\bar{y})^2}}$
    $$r = \frac{270}{\sqrt{90 \times 1000}}$$
    $$r = \frac{270}{300} = 0.9$$
    3. 결정계수 $R^2$: $R^2 = r^2$
    $$R^2 = 0.9^2$$
    $$R^2 = 0.81$$
    4. $\sigma^2$의 불편추정량 $s^2$: $s^2 = \frac{\sum(y_i-\bar{y})^2 - \beta^2 \sum(x_i-\bar{x})^2}{n-2}$
    $$s^2 = \frac{1000 - 3^2 \times 90}{10-2}$$
    $$s^2 = \frac{1000 - 810}{8} = \frac{190}{8} = 23.75$$
    따라서 $\sigma^2$의 불편추정량이 $190/9$라고 설명한 내용은 틀렸습니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

18. 다음 표에서 x′와 y′는 각각 설명변수(x)와 반응변수(y)를 표준화한 변수 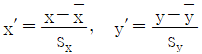의 자료이다.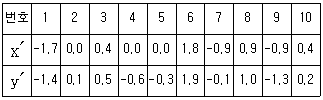

위의 표준화된 변수 (x′, y′)에 대해 단순선형회귀분석을 최소제곱법으로 수행할 때, 회귀계수의 추정값에 대한 설명으로 옳은 것은? (단, 는 각각 x, y의 표본평균이고, sx, sy는 각각 x, y의 표본표준편차이고, sx≠sy이다)

  1. 원 변수 (x, y)에 대한 회귀계수의 추정값과 동일하다.
  2. 원 변수 (x, y)에 대한 회귀계수의 추정값의 역수와 동일하다.
  3. 원 변수 (x, y)의 상관계수와 동일하다.
  4. 원 변수 (x, y)의 결정계수와 동일하다.
(정답률: 44%)
  • 변수를 표준화하여 단순선형회귀분석을 수행할 때, 표준화된 변수 $x'$와 $y'$ 사이의 회귀계수 $\beta'$는 원 변수 $x, y$의 상관계수 $r$과 동일한 값을 가집니다.
    표준화 공식 $\text{x}' = \frac{x - \bar{x}}{s_x}$, $\text{y}' = \frac{y - \bar{y}}{s_y}$를 적용하면 회귀계수 추정값은 다음과 같이 유도됩니다.
    $$\beta' = r \frac{s_{y'}}{s_{x'}} = r \frac{1}{1} = r$$
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

19. 가지 종류의 유기농 세제(A, B, C)에 대해 박테리아의 성장을 지연시키는 효과를 비교하고자 한다. 실험실에서 하루에 3번의 실험만 가능하므로 실험일 월, 화, 수, 목을 블록으로 하여 확률화완전블록설계를 실시하여 다음과 같은 결과를 얻었다. 분산분석을 이용하여 세제 종류별 박테리아 성장 지연 효과의 차이를 검정하고자 한다. 분석결과에 대한 설명으로 옳은 것만을 모두 고르면?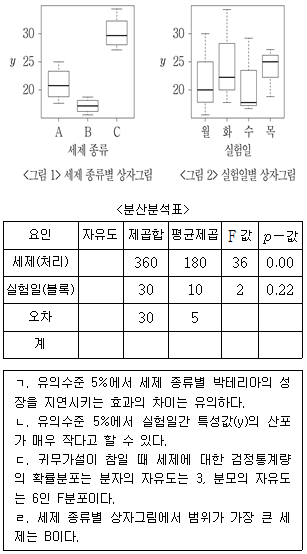

  1. ㄱ, ㄴ
  2. ㄱ, ㄷ
  3. ㄱ, ㄴ, ㄷ
  4. ㄴ, ㄷ, ㄹ
(정답률: 56%)
  • 분산분석표와 상자그림 을 분석합니다.
    ㄱ. 세제(처리)의 $p$-값이 $0.00$으로 유의수준 $0.05$보다 작으므로, 세제 종류별 효과의 차이는 유의합니다.
    ㄴ. 실험일(블록)의 $p$-값이 $0.22$로 유의수준 $0.05$보다 크므로, 실험일 간의 차이는 유의하지 않으며 산포가 작다고 볼 수 있습니다.

    오답 노트
    ㄷ: 세제의 자유도는 $3-1=2$이며, 오차의 자유도는 전체 자유도에서 세제와 실험일 자유도를 뺀 값입니다.
    ㄹ: 세제 종류별 상자그림에서 범위가 가장 큰 세제는 C입니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

20. 어떤 직육면체 주사위의 1의 눈이 있는 면이 작아서 1의 눈이 나올 확률 p가 1/6보다 작을 것으로 예상된다. 이에 대한 가설 H0 : p=1/6 대 H1 : p＜1/6을 검정하기 위해 이 주사위를 10번 던져 1의 눈이 나온 횟수를 확률변수 Y라 할 때, 옳은 것은?

  1. Y/10는 p의 불편추정량(unbiased estimator)이 아니다.
  2. Y의 관측값이 클수록 귀무가설을 기각한다.
  3. Y의 확률분포는 이항분포 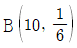을 따른다.
  4. Y의 관측값이 2일 때 유의확률(p-값)은 P(X≤2)이다. 단, 확률변수 X는 이항분포 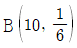을 따른다.
(정답률: 27%)
  • 귀무가설 $H_0: p=1/6$ 하에서 관측값 $y$에 대한 유의확률(p-value)은 귀무가설이 참일 때 관측값보다 더 극단적인 값이 나올 확률입니다. 대립가설이 $p < 1/6$인 좌측검정이므로, 관측값이 2일 때 유의확률은 $P(Y \le 2)$가 됩니다. 이때 $Y$는 귀무가설 하의 분포인 이항분포 를 따르는 확률변수 $X$로 표현합니다.

    오답 노트
    Y/10는 p의 불편추정량임
    관측값이 작을수록 귀무가설 기각 가능성 높음
    Y의 확률분포는 실제 확률 $p$를 포함한 $B(10, p)$를 따름
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

< 이전회차목록 다음회차 >