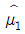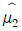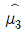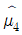9급 국가직 공무원 통계학개론 필기 기출문제복원 (2024-03-23)

9급 국가직 공무원 통계학개론
(2024-03-23 기출문제)

목록

1과목: 과목 구분 없음

1. 다음은 대통령 선거 출구 조사 방법에 대한 설명이다. 이에 해당하는 표본 추출 기법은?

  1. 단순임의추출법(simple random sampling)
  2. 계통추출법(systematic sampling)
  3. 층화임의추출법(stratified random sampling)
  4. 집락추출법(cluster sampling)
(정답률: 알수없음)
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

2. 세 사건 A, B, C가 서로 독립이고 P(A)=1/4, P(B)=3P(C), P(A∩Bc∩C)=1/48 일 때, P(B∩Cc)는?

  1. 1/12
  2. 5/12
  3. 7/12
  4. 11/12
(정답률: 알수없음)
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

3. 확률변수 X, Y에 대하여 E[X(Y+1)]=9, E[Y(X+1)]=10, E(X+Y)=7일 때, 공분산 Cov(X, Y)의 값은?

  1. －6
  2. －5
  3. 5
  4. 6
(정답률: 알수없음)
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

4. '두 확률변수 X, Y의 상관계수가 0', 즉 'Corr(X, Y)=0'과 동치가 아닌 것은?

  1. Var(X+Y) = Var(X-Y)
  2. E(XY) = E(X)E(Y)
  3. Cov(-2X+3, 3Y-2) = 0
  4. Cov)X+Y, X-Y) = 0
(정답률: 알수없음)
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

5. 두 연속확률변수 X, Y의 상관계수에 대한 설명으로 옳지 않은 것은?

  1. 상관계수가 0이면 X, Y는 독립이다.
  2. 상관계수는 측정단위의 영향을 받지 않는다.
  3. 상관계수가 －0.7인 경우가 ＋0.5인 경우보다 선형관계가 강하다.
  4. X, Y의 표본상관계수가 0.5일 때, 동일 자료에서 3X와 5Y의 표본상관계수도 0.5이다.
(정답률: 알수없음)
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

6. 정규분포 N(μ, σ2)에서 표준편차(σ)를 이용하여 사분위수범위를 나타낸 것으로 옳은 것은? (단, zα는 표준정규분포의 제 100×(1-α)백분위수이다)

  1. z0.025 × σ
  2. z0.25 × σ
  3. 2 × z0.025 × σ
  4. 2 × z0.25 × σ
(정답률: 알수없음)
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

7. 미지의 모평균이 μ이고 모분산이 σ2인 모집단으로부터 확률표본 X1, X2, X3, X4를 추출하여 μ에 대한 점추정량을 다음과 같이 정의하였다. 이 점추정량 중에서 μ에 대한 불편추정량이면서 그중 최소분산을 갖는 것은? (단, σ2 ＞ 0 이다)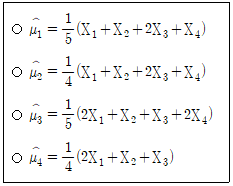

(정답률: 알수없음)
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

8. 확률변수 X의 확률분포가 다음과 같다.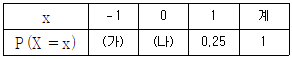

다음 항목 중 옳은 것만을 모두 고르면?

  1. ㄱ
  2. ㄴ
  3. ㄱ, ㄷ
  4. ㄴ, ㄷ
(정답률: 알수없음)
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

9. 독립변수 X와 종속변수 Y를 갖는, 절편이 있는 단순선형회귀모형에서 최소제곱법을 적용했을 때, 결정계수에 대한 설명으로 옳은 것은?

  1. 결정계수가 0이면 모든 잔차가 0이다.
  2. 결정계수가 큰 모형일수록 설명력이 낮은 모형이다.
  3. 결정계수는 X, Y의 표본상관계수를 이용하여 구할 수 있다.
  4. 만약 새로운 독립변수를 모형에 추가한다면 결정계수는 감소한다.
(정답률: 알수없음)
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

10. 어느 도시의 고등학생 중 남학생 100명과 여학생 100명을 무작위추출한 뒤 수학과 영어 과목에 대한 선호도를 조사하여 다음과 같은 분할표를 얻었다. “성별에 따라 과목 선호도에 차이가 없다.”라는 귀무가설을 검정하기 위한 카이제곱검정통계량의 값이 8일 때, (가)의 값과 귀무가설 하에서의 이 검정통계량의 근사적인 분포를 바르게 연결한 것은? (단, (가)≥50 이다)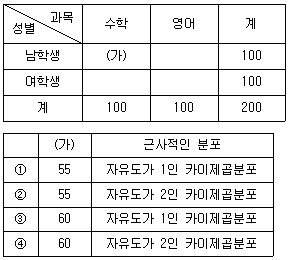

  1. ①
  2. ②
  3. ③
  4. ④
(정답률: 알수없음)
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

11. 어느 도시에서 하루에 발생하는 교통사고 건수를 지난 200일 동안 조사하여 다음 표와 같이 정리하였다.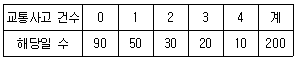

이 자료에서 구한 하루 발생 교통사고 건수의 통계량의 값으로 옳지 않은 것은?

  1. 평균은 1.05이다.
  2. 중앙값은 1이다.
  3. 최빈값은 0이다.
  4. 제3사분위수는 3이다.
(정답률: 알수없음)
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

12. 분산이 같은 두 정규모집단 A와 B로부터 크기가 각각 8인 확률표본을 독립적으로 추출하였더니 표본분산이 각각 19와 13이었다. 두 모평균의 차 μA - μB에 대한 95% 신뢰구간의 길이는? (단, tα(k)는 자유도가 k인 t분포의 제 100×(1-α)백분위수를 나타내고, t0.025(7)=2.365, t0.025(14)=2.145이다)

  1. 4.29
  2. 4.73
  3. 8.58
  4. 9.46
(정답률: 알수없음)
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

13. 앞면이 나올 확률이 p인 동전에 대해 가설 H0 : p = 1/2, H1 : p ＞ 1/2 을 검정하려고 한다. 이 동전을 다섯 번 던져 보니 앞면이 네 번 나왔다면, 유의확률(p－value)은?

  1. 1/16
  2. 2/16
  3. 3/16
  4. 4/16
(정답률: 알수없음)
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

14. 다음은 연령대별로 스마트폰 과의존 위험군 비율을 조사한 것이다.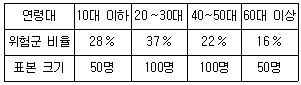

이 자료를 바탕으로 다음의 가설을 검정하고자 한다.

귀무가설 H0가 참일 때 구한, 위험군에 속하는 사람 수의 추정된 기대도수와 관측도수 간에 차이가 존재한다. 이 차이의 절댓값이 가장 큰 연령대는?

  1. 10대 이하
  2. 20~30대
  3. 40~50대
  4. 60대 이상
(정답률: 알수없음)
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

15. 어느 마트에서 특정 상품에 대한 진열대의 높이와 폭이 매출액에 영향을 주는지 알아보기 위해, 진열대 높이(A)를 상, 중, 하 3수준으로, 폭(B)을 대, 소 2수준으로 하여 실험하였다. 다른 조건들이 동일한 12일 동안 6개의 실험조건을 무작위 순서로 2일씩 적용하여 매출액을 조사한 후 얻은 분산분석표가 다음과 같다. 이에 대한 설명으로 옳지 않은 것은?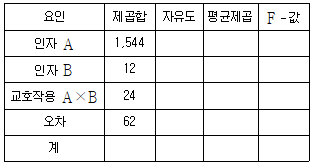

  1. 총제곱합은 1,642이다.
  2. 인자 B의 평균제곱은 교호작용 A×B의 평균제곱과 동일하다.
  3. 오차 자유도는 6이다.
  4. 유의성검정에서의 유의확률은 인자 A가 교호작용 A×B 보다 크다.
(정답률: 알수없음)
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

16. 다음은 자료 (x1i, x2i, yi) (i = 1, 2, …, 23)에 다중선형회귀모형 yi = β0 + β1x1i + β2x2i + εi를 최소제곱법으로 적합하여 얻은 분산분석표이다. 이에 대한 설명으로 옳은 것만을 모두 고르면? (단, εi는 N(0, σ2)을 따르고 서로 독립이다)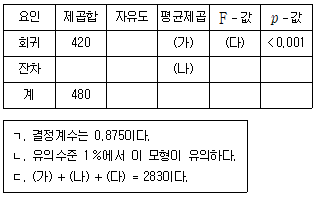

  1. ㄱ, ㄴ
  2. ㄱ, ㄷ
  3. ㄴ, ㄷ
  4. ㄱ, ㄴ, ㄷ
(정답률: 알수없음)
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

17. 다음 설명 중 옳지 않은 것은?

  1. 유의수준 α=0.01에서 귀무가설을 기각하는 검정 결과가 나왔다면 유의수준 α=0.05에서도 귀무가설을 기각하게 된다.
  2. 모든 자연수 n에 대해 t0.05(n) ＜ t0.05(n+1)이다(단, t0.05(k)는 자유도가 k인 t분포의 제95백분위수).
  3. 모든 자연수 n에 대해 χ20.05(n) ＜ χ20.05(n+1)이다(단, χ20.05(k)는 자유도가 k인 카이제곱분포의 제95백분위수).
  4. 두 사건 A1, A2가 서로 배반이고 P(B) ＞ 0 일 때, 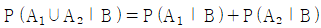이다.
(정답률: 알수없음)
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

18. 다음은 자료 (xi, yi) (i = 1, 2, …, n)에 단순선형회귀모형 yi = β0 + β1xi + εi를 적합하여 구할 수 있는 값들이다.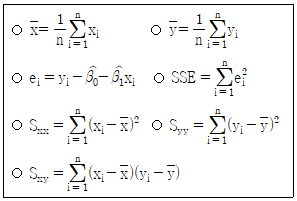

다음 식 중 옳은 것은? (단, 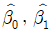은 각각 β0, β1의 최소제곱추정값이다)

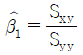
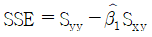
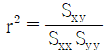  3. (단, r2은 결정계수)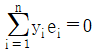
(정답률: 알수없음)
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

19. 두 이산확률변수 X, Y의 결합확률질량함수가 다음과 같을 때, P(Y=2X)의 값은? (단, c는 상수이다)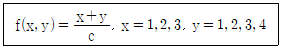

  1. 1/18
  2. 1/9
  3. 1/6
  4. 2/9
(정답률: 알수없음)
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

20. 수준이 3개이고 반복수가 각각 n1=5, n2=10, n3=15인 일원배치법으로부터 얻은 자료를 yij(i=1,2,3, j=1,2,…,ni)라 하고, i번째 수준에서의 평균을 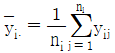라 하자. 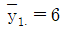, , 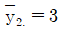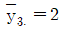일 때, 분산분석표에서 처리제곱합은?

  1. 60
  2. 90
  3. 270
  4. 330
(정답률: 알수없음)
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

목록 다음회차 >