9급 국가직 공무원 화학공학일반 필기 기출문제복원 (2022-04-02)

9급 국가직 공무원 화학공학일반
(2022-04-02 기출문제)

목록

1. 기체의 농도 400ppm에 해당하는 백분율 농도[%]는?

  1. 4
  2. 0.4
  3. 0.04
  4. 0.004
(정답률: 알수없음)
  • ppm은 백만분율을 의미하므로, 400ppm는 0.04%에 해당합니다. 따라서 정답은 "0.04"입니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

2. 밸브(valve)에 대한 설명으로 옳지 않은 것은?

  1. 체크 밸브(check valve)는 역류를 방지하기 위해 사용된다.
  2. 글로브 밸브(globe valve)는 유체의 흐름을 수직방향으로 바꾸기 위해 사용된다.
  3. 안전 밸브(safety valve)는 유체의 압력이 설정 압력을 초과하면 개방된다.
  4. 게이트 밸브(gate valve)가 반 정도 열렸을 때에는 유체의 흐름이 흐트러져서 와류가 생길 수 있다.
(정답률: 알수없음)
  • 글로브 밸브(globe valve)는 유체의 흐름을 수직방향으로 바꾸기 위해 사용되는 것이 아니라, 유체의 양을 조절하기 위해 사용된다. 따라서 "글로브 밸브(globe valve)는 유체의 흐름을 수직방향으로 바꾸기 위해 사용된다."가 옳지 않은 설명이다.

    글로브 밸브는 유체의 흐름을 제어하기 위해 유체의 흐름 방향과 수직 방향으로 움직이는 디스크를 이용한다. 디스크가 밸브 바디 안쪽으로 움직이면 유체의 흐름이 막히고, 디스크가 밸브 바디 바깥쪽으로 움직이면 유체가 흐르게 된다. 따라서 글로브 밸브는 유체의 양을 조절하기 위해 사용된다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

3. 흑체의 온도를 2,000K에서 1,500K으로 낮출 때, 2,000K 대비 1,500K에서 방출되는 복사에너지의 비는?

  1. 81/256
  2. 9/16
  3. 16/9
  4. 256/81
(정답률: 알수없음)
  • 복사에너지는 온도의 4제곱에 비례한다는 슈테판-볼츠만 법칙에 따라 계산할 수 있다. 따라서 온도가 2,000K에서 1,500K로 낮아지면 복사에너지는 (1,500/2,000)^4 = 81/256배로 감소한다. 따라서 정답은 "81/256"이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

4. 이상 반응기(ideal reactor)에 대한 설명으로 옳지 않은 것은?

  1. 반응기 내 온도와 반응물의 농도는 반응속도에 영향을 주는 인자이다.
  2. 회분식 반응기에서는 반응시간에 따라 반응물의 농도가 달라진다.
  3. 플러그 흐름 반응기(PFR)에서는 반응물이 흘러가며 반응이 일어난다.
  4. 연속교반 탱크 반응기(CSTR)는 정상상태에서 반응기 내부와 출구의 반응물 농도가 다르다.
(정답률: 알수없음)
  • 연속교반 탱크 반응기(CSTR)는 정상상태에서 반응기 내부와 출구의 반응물 농도가 다르다는 설명이 옳지 않습니다. CSTR은 균일한 혼합을 유지하면서 반응이 일어나는 반응기로, 정상상태에서는 반응기 내부와 출구의 반응물 농도가 동일합니다. 따라서 이 보기가 옳지 않습니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

5. 다음 중 차원(dimension)이 다른 것은?

  1. 열용량(heat capacity)
  2. 기체 상수(gas constant)
  3. 몰 엔트로피(molar entropy)
  4. 볼츠만 상수(Boltzmann constant)와 아보가드로 상수(Avogadro constant)의 곱
(정답률: 알수없음)
  • 열용량(heat capacity)은 에너지의 양을 나타내는 물리량으로, 온도 변화에 따른 열의 흡수나 방출을 나타내는 값입니다. 따라서 다른 세 개의 보기는 모두 단위가 에너지/온도 또는 분자/온도 등으로 표현되는 차원을 가지고 있지만, 열용량은 에너지/온도^2의 차원을 가지고 있습니다. 따라서 열용량(heat capacity)이 다른 것입니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

6. 그림과 같은 구조의 원형관 속에서 비압축성 유체의 흐름이 정상상태 층류이고, 직경이 d인 2개의 관 속 유체의 거동은 같다. 직경이 4d인 관의 중심지점 A를 지나는 유체의 질량속도가 2kgs-1m-2일 때, 직경이 d인 관의 중심지점 B를 지나는 유체의 질량속도[kgs-1m-2]는? (단, 마찰손실은 무시한다.)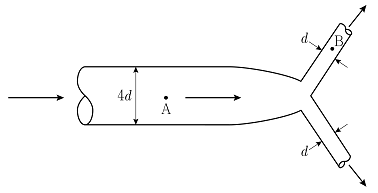

  1. 1
  2. 4
  3. 8
  4. 16
(정답률: 알수없음)
  • 직경이 4d인 관에서의 질량속도는 2kgs-1m-2이므로, 관의 흐름율은 다음과 같습니다.

    Q = Av = π(2d)2/4 × 2k = 2πdk

    여기서 A는 단면적, v는 속도입니다. 따라서, 직경이 d인 관에서의 흐름율은 다음과 같습니다.

    Q' = Av' = πd2/4 × v'

    두 관의 유체 거동이 같으므로, 흐름율은 동일합니다.

    Q = Q'

    2πdk = πd2/4 × v'

    v' = 8k/d

    따라서, 직경이 d인 관에서의 질량속도는 다음과 같습니다.

    v' = 8k/d = 8 × 2 = 16 [kgs-1m-2]

    따라서, 정답은 "16"입니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

7. 단면적이 일정한 원통형 수평관을 흐르는 유체에 Hagen-Poiseuille 식이 적용될 때, 관의 반지름, 관의 길이, 압력차(∆P)가 각각 2배로 커지면 부피 유량은 몇 배로 커지는가? (단, 유체의 점도는 일정하다.)

  1. 2
  2. 4
  3. 8
  4. 16
(정답률: 알수없음)
  • Hagen-Poiseuille 식은 다음과 같다.

    Q = πr⁴∆P/8ηL

    여기서 Q는 부피 유량, r은 반지름, ∆P는 압력차, η는 점도, L은 길이를 나타낸다.

    문제에서 반지름, 길이, 압력차가 각각 2배로 커진다고 했으므로,

    Q' = π(2r)⁴(2∆P)/8η(2L)

    = 16πr⁴∆P/8ηL

    = 16Q

    따라서 부피 유량은 16배로 커진다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

8. 유체의 열확산계수(thermal diffusivity)에 대한 설명으로 옳지 않은 것은?

  1. m2s-1을 단위로 사용할 수 있다.
  2. 유체의 열전도도, 밀도, 점도를 이용하여 계산할 수 있다.
  3. 다른 조건이 같을 때, 유체의 밀도가 클수록 열확산계수는 더 작다.
  4. 유체 운동이 없을 때의 열확산식(heat diffusion equation)에서 계수로 사용된다.
(정답률: 알수없음)
  • "유체의 열전도도, 밀도, 점도를 이용하여 계산할 수 있다."가 옳지 않은 설명입니다. 열확산계수는 열전도도, 밀도, 점도와 같은 물성값들로부터 계산될 수 있지만, 직접적으로 측정되는 값이며, m2s-1을 단위로 사용합니다. 따라서, "유체의 열전도도, 밀도, 점도를 이용하여 계산할 수 있다."는 잘못된 설명입니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

9. 단면적 0.1m2, 길이 2m의 원형 칼럼(column) 내부에 밀도 1,000kgm-3인 흡착제 A와 밀도 2,500kgm-3인 흡착제 B를 각각 1m씩 충진하였다. 흡착제 A와 B의 질량이 각각 60kg과 50kg일 때, 전체 칼럼 내부의 공극률(voidage)[%]은? (단, 흡착제 A와 B는 서로 섞이지 않는다.)

  1. 30
  2. 40
  3. 50
  4. 60
(정답률: 알수없음)
  • 전체 칼럼 내부의 체적은 πr2h = 0.1m2 × 2m = 0.2m3이다.
    흡착제 A의 체적은 πr2h/2 = 0.05m2 × 2m = 0.1m3이고,
    흡착제 B의 체적은 전체 체적에서 흡착제 A의 체적을 뺀 값인 0.2m3 - 0.1m3 = 0.1m3이다.

    따라서, 흡착제 A의 밀도는 60kg/0.1m3 = 600kg/m3이고,
    흡착제 B의 밀도는 50kg/0.1m3 = 500kg/m3이다.

    공극률은 전체 체적에서 흡착제 A와 B의 체적을 뺀 값인 공간의 체적 대비 토출체적의 비율이므로,

    공극률 = (전체 체적 - 흡착제 A의 체적 - 흡착제 B의 체적) / 전체 체적 × 100%
    = (0.2m3 - 0.1m3 - 0.1m3) / 0.2m3 × 100%
    = 0.0 × 100%
    = 0%

    따라서, 정답은 "0"이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

10. 지열을 이용하는 카르노 열펌프(Carnot heat pump)로 온실을 난방하고 있다. 지열의 열원 온도가 280K이고 온실의 열손실이 6kW일 때, 온실 온도를 300K으로 유지하기 위해 열펌프를 가동하는 데 필요한 최소 동력의 양[W]은?

  1. 375
  2. 400
  3. 425
  4. 450
(정답률: 알수없음)
  • 카르노 열펌프의 효율은 다음과 같이 주어진다.

    η = 1 - T2/T1

    여기서 T1은 열원의 온도, T2는 열펌프가 제공하는 열의 온도이다. 온실의 열손실은 6kW이므로, 열펌프가 제공해야 하는 열의 양은 6kW이다. 따라서,

    T2 = T1 - Q/ΔS

    여기서 Q는 열펌프가 제공해야 하는 열의 양, ΔS는 열펌프의 엔트로피 변화량이다. 열펌프의 엔트로피 변화량은 0이므로,

    T2 = T1 - Q/ΔS = T1 - Q/0 = T1

    따라서, 열펌프가 제공하는 열의 온도는 280K이다. 온실 온도를 300K로 유지하기 위해서는 열펌프가 제공하는 열의 양이 6kW보다 커야 한다. 따라서, 열펌프가 제공하는 열의 양을 6kW로 유지하면서 온실 온도를 300K로 유지하기 위해서는 열펌프가 소비하는 최소 동력의 양이 400W이다.

    P = Q/η = Q/(1 - T2/T1) = 6kW/(1 - 280K/300K) = 400W
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

11. 대형 개방 탱크 바닥에 연결된 2개의 소형 노즐 A, B를 통하여 물을 동시에 배출시킨다. 노즐 A의 단면적이 노즐 B의 단면적의 2배일 때, 노즐 출구의 유속[ms-1]과 유량[m3s-1]에 대한 설명으로 옳은 것은? (단, 마찰손실은 무시한다.)

  1. 노즐 A와 노즐 B의 출구 유속은 같다.
  2. 노즐 A와 노즐 B의 출구 유량은 같다.
  3. 노즐 출구의 유속은 중력가속도와 무관하다.
  4. 노즐 B의 출구 유속은 노즐 A의 출구 유속의 2배이다.
(정답률: 알수없음)
  • 노즐 A와 노즐 B는 같은 탱크에서 물을 공급받으므로, 물의 질량은 동일하다. 따라서, 노즐 A와 노즐 B의 유량은 같다. 유량은 유속과 단면적의 곱으로 나타낼 수 있으므로, 노즐 A와 노즐 B의 출구 유속은 같다. 따라서, "노즐 A와 노즐 B의 출구 유속은 같다."가 옳은 설명이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

12. 0.5M의 NaOH 용액 5L를 완전히 중화하는 데 필요한 0.1M H2SO4 용액의 부피[L]는?

  1. 5
  2. 12.5
  3. 25
  4. 37.5
(정답률: 알수없음)
  • NaOH와 H2SO4는 1:2 몰비로 반응하므로, NaOH 용액의 몰수는 다음과 같습니다.

    0.5M NaOH × 5L = 2.5 몰

    따라서, 중화 반응에 필요한 H2SO4 용액의 몰수는 2.5 몰 × 2 = 5 몰입니다.

    이제, H2SO4 용액의 몰수와 농도를 알고 있으므로 다음과 같이 부피를 계산할 수 있습니다.

    부피 = 몰수 ÷ 농도 = 5 몰 ÷ 0.1 M = 50 L

    하지만, 이는 NaOH 용액의 부피보다 큰 값입니다. 중화 반응에서는 NaOH와 H2SO4가 1:2 몰비로 반응하므로, H2SO4 용액의 부피는 NaOH 용액의 부피의 절반인 2.5 L이 됩니다.

    따라서, 정답은 2.5 L을 10으로 곱한 25가 아니라, 5로 나눈 12.5입니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

13. 화학공장 운영에 관한 비용추정에서 총생산비용을 제조비용과 일반경비로만 분류할 때, 일반경비에 해당하는 것은?

  1. 생산설비의 감가상각비
  2. 생산 제품의 운송 및 판매비용
  3. 제품 생산을 위한 원료 구입비
  4. 제품 생산을 위한 특허 사용료
(정답률: 알수없음)
  • 일반경비는 제조과정에서 발생하는 간접비용으로, 생산설비의 감가상각비, 제품 생산을 위한 원료 구입비, 제품 생산을 위한 특허 사용료 등이 해당됩니다. 따라서, 생산 제품의 운송 및 판매비용은 직접비용으로 분류되어야 하며, 일반경비에 해당하지 않습니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

14. 피드백(feedback) 제어에 대한 설명으로 옳지 않은 것은?

  1. 비례(P) 제어기에서는 잔류편차(offset)가 존재한다.
  2. 비례－적분(PI) 제어기에서는 정상상태에서 잔류편차가 없어진다.
  3. 비례－미분(PD) 제어기에서 미분 동작은 빠른 시간 내에 잔류편차를 제거한다.
  4. 비례－적분－미분(PID) 제어기는 느린 제어 공정인 온도 및 농도 제어에 널리 이용된다.
(정답률: 알수없음)
  • "비례－미분(PD) 제어기에서 미분 동작은 빠른 시간 내에 잔류편차를 제거한다."가 옳지 않은 것입니다.

    미분 동작은 변화율을 계산하여 제어량의 변화를 예측하는 역할을 합니다. 따라서 미분 동작은 제어량의 변화가 빠를 때 유용하게 사용됩니다. 하지만 잔류편차는 제어량이 일정한 값을 유지하는 상태이므로 미분 동작이 효과적이지 않습니다. 따라서 PD 제어기에서는 잔류편차를 제거하기 위해 비례 제어기와 함께 사용되는 경우가 많습니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

15. 단일 성분의 다상계 평형(multiphase equilibrium)에 대한 설명으로 옳지 않은 것은?

  1. 삼중점에서 자유도는 0이다.
  2. 기체는 임계온도 이상에서 응축될 수 있다.
  3. 이슬점에서 온도가 내려가면 평형 상태의 증기가 응축된다.
  4. 순수한 성분의 증기와 액체가 평형 상태일 때의 압력이 증기압이다.
(정답률: 알수없음)
  • "기체는 임계온도 이상에서 응축될 수 있다."가 옳지 않은 설명입니다. 이는 임계온도 이상에서 기체는 액체나 고체로 변화하지 않고 기체 상태를 유지합니다. 임계온도 이하에서 기체는 압력이 일정한 상태에서 액체로 응축됩니다.

    이유는 기체 상태에서 분자들은 서로 간격이 멀어서 서로 충돌하지 않고 자유롭게 움직입니다. 그러나 액체 상태에서는 분자들이 서로 가까이 붙어서 서로 충돌하며 움직입니다. 따라서 기체 상태에서는 액체 상태로 변화하기 위해서는 분자들이 서로 충돌하여 운동에너지를 상대적 운동에너지로 전달해야 합니다. 이는 압력이 일정한 상태에서 온도를 낮추면 일어나는 현상입니다. 이러한 현상을 증류라고 합니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

16. 상대 습도에 대한 설명으로 옳은 것은?

  1. 포화 습도에 대한 절대 습도의 비이다.
  2. 수증기로 포화된 공기의 절대 습도를 의미한다.
  3. 수증기의 포화 증기압에 대한 수증기 분압의 비이다.
  4. 건조 기체 1kg에 동반되는 수증기의 질량을 kg수로 나타낸 것이다.
(정답률: 알수없음)
  • 상대 습도는 공기 안에 포함된 수증기의 양이 현재 상황에서 최대한의 양에 비해 얼마나 많은지를 나타내는 지표입니다. 이를 수식으로 나타내면 상대 습도 = (현재 수증기 분압 / 포화 수증기 분압) x 100% 입니다. 따라서 "수증기의 포화 증기압에 대한 수증기 분압의 비이다."가 옳은 설명입니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

17. 단일 유체가 원통형 관 내부에서 난류(turbulent flow)로 흐를 때, 벽(wall) 근처와 난류중심(turbulent core)에서의 속도구배와 온도구배에 대한 설명으로 옳은 것은?

  1. 속도구배와 온도구배는 벽 근처보다 난류중심에서 더 작다.
  2. 속도구배와 온도구배는 벽 근처보다 난류중심에서 더 크다.
  3. 속도구배는 벽 근처보다 난류중심에서 더 크며, 온도구배는 벽 근처보다 난류중심에서 더 작다.
  4. 속도구배는 벽 근처보다 난류중심에서 더 작으며, 온도구배는 벽 근처보다 난류중심에서 더 크다.
(정답률: 알수없음)
  • 정답은 "속도구배와 온도구배는 벽 근처보다 난류중심에서 더 작다."입니다.

    이유는 다음과 같습니다. 난류는 유체의 불규칙한 운동으로, 속도와 온도가 고르게 분포되어 있지 않습니다. 따라서 난류 중심에서는 유체의 속도와 온도가 비교적 균일하게 분포되어 있습니다. 반면에 벽 근처에서는 유체가 벽과 마찰하면서 속도와 온도가 변화하게 되므로, 속도구배와 온도구배가 더 크게 나타납니다. 따라서 속도구배와 온도구배는 벽 근처보다 난류중심에서 더 작다는 것이 옳습니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

18. Stokes 법칙이 적용되는 밀도 1kgm-3, 점도 2×10-5kgm-1s-1의 유체 내 구형 단일입자가 중력에 의해 자유침강(free settling)하고 있다. 구형입자의 종말속도는 2×10-3ms-1이고 항력계수(drag coefficient)가 1,000일 때, 입자의 지름[mm]은?

  1. 0.24
  2. 0.48
  3. 2.4
  4. 4.8
(정답률: 알수없음)
  • Stokes 법칙은 다음과 같이 표현됩니다.

    v = (2/9) * (ρp - ρf) * g * r2 / η

    여기서, v는 입자의 종말속도, ρp는 입자의 밀도, ρf는 유체의 밀도, g는 중력가속도, r은 입자의 반지름, η는 유체의 점도입니다.

    문제에서 주어진 값들을 대입하면,

    2×10-3 = (2/9) * (1000 - 1) * 9.81 * r2 / (2×10-5)

    r2 = (2×10-3 * 2×10-5 * 9.81) / (2/9 * 999)

    r2 = 1.08×10-8

    r = 1.04×10-4 m = 0.104 mm

    따라서, 입자의 지름은 2r = 0.208 mm 이므로, 보기에서 가장 근접한 값은 0.24입니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

19. 그림 (가), (나)와 같이 2개의 단열재가 직렬로 연결된 평면 벽을 통한 정상상태 열전도가 있다. (가)와 (나)에서 벽의 두께 방향으로의 열흐름속도 및 열흐름면적이 같을 때, (가)의 온도구배 △T1과 (나)의 온도구배 △T2의 비(△T1/△T2)는? (단, d와 k는 각각 임의의 벽 두께와 열전도도 값이다.)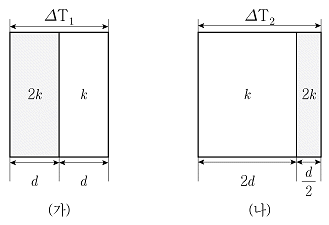

  1. 1/3
  2. 1/2
  3. 2/3
  4. 3/4
(정답률: 알수없음)
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

20. 비반응속도가 1h-1인 1차 비가역 액상반응 A → B가 일어나는 연속교반 탱크 반응기(CSTR)를 등온의 정상상태에서 4h의 공간시간으로 운전하고 있다. 기존 반응기와 같은 전환율을 얻을 수 있는 신규 CSTR을 설계할 때 새로운 촉매를 사용하여 비반응속도를 2.5h-1로 증가시켰다면, 기존 반응기 대비 신규 반응기의 부피 비는? (단, 반응물, 공급 유량, 운전 온도는 기존 반응기와 신규 반응기에서 같다.)

  1. 0.4
  2. 0.5
  3. 0.6
  4. 0.7
(정답률: 알수없음)
  • 1차 비가역 반응에서 전환율은 다음과 같이 표현할 수 있다.

    X = 1 - e-kτ

    여기서 X은 전환율, k는 비반응속도, τ는 공간시간이다.

    기존 반응기에서 전환율 X1을 얻기 위해서는,

    X1 = 1 - e-kτ1

    신규 반응기에서 전환율 X2를 얻기 위해서는,

    X2 = 1 - e-kτ2

    여기서 k2 = 2.5h-1 이고, τ1 = τ2 = 4h 이므로,

    X2 = 1 - e-2.5×4 ≈ 0.78

    기존 반응기에서 전환율 X1을 X2와 같게 만들기 위해서는,

    1 - e-kτ1 = 0.78

    e-kτ1 = 0.22

    -kτ1 = ln(0.22)

    τ1 = -ln(0.22)/k ≈ 1.6h

    따라서, 새로운 반응기의 공간시간은 1.6h 이다.

    부피 비는 다음과 같이 계산할 수 있다.

    V2/V1 = τ2/τ1 = 4/1.6 ≈ 2.5

    따라서, 새로운 반응기의 부피는 기존 반응기의 2.5배이므로, 부피 비는 0.4이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

목록 다음회차 >