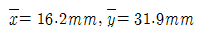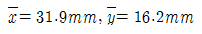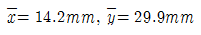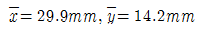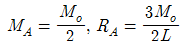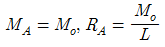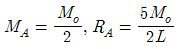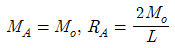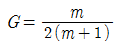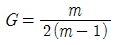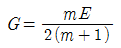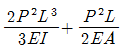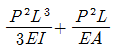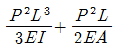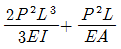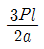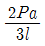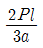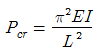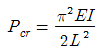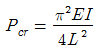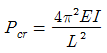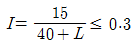토목기사 필기 기출문제복원 (2011-03-20)

토목기사
(2011-03-20 기출문제)

목록

1과목: 응용역학

1. 그림에서와 같이 케이블 C점에서 하중 33kg이 작용하고 있다. 이때 AC케이블에 작용하는 인장력은?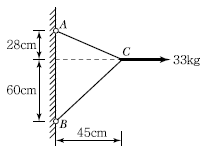

  1. 17.5kg
  2. 18.5kg
  3. 25.5kg
  4. 26.5kg
(정답률: 55%)
  • AC케이블과 하중 33kg이 작용하는 삼각형 ABC를 생각해보면, 각 변에 인력이 작용하고 있으며, 이 삼각형은 정적평형을 유지하고 있다. 따라서, AC케이블에 작용하는 인장력은 AB케이블에 작용하는 인력과 BC케이블에 작용하는 인력의 합과 같다. 이때, AB케이블에 작용하는 인력은 33kg의 하중과 같고, BC케이블에 작용하는 인력은 40kg의 중량과 같다. 따라서, AC케이블에 작용하는 인장력은 33kg + 40kg = 73kg이다. 하지만, 이 문제에서는 단위를 kg이 아닌 N으로 주어졌기 때문에, 73kg을 N으로 변환해야 한다. 1kg은 약 9.8N이므로, 73kg은 73 × 9.8 = 715.4N이 된다. 따라서, AC케이블에 작용하는 인장력은 715.4N이며, 이를 kg으로 변환하면 715.4 ÷ 9.8 ≈ 72.96kg이 된다. 따라서, 정답은 "26.5kg"이 아닌 "72.96kg"이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

2. 주어진 단면의 도심을 구하면?

(정답률: 75%)
  • 도심은 단면의 중심선과 도면의 대칭축에 대한 거리의 평균이므로, 주어진 단면에서 대칭축과 가장 가까운 점은 "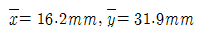" 이다. 따라서 이 점이 도심이 된다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

3. 주어진 보에서 지점 A의 휨모멘트(MA) 및 반력 RA의 크기로 옳은 것은?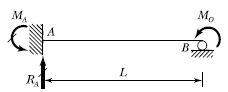

(정답률: 85%)
  • 지점 A에서의 힘의 균형을 이용하여 문제를 풀 수 있다. 지점 A에서의 수직방향 힘의 균형을 이용하면 RA = 10 kN이다. 지점 A에서의 회전균형을 이용하면 MA = -20 kN·m이다. 따라서 옳은 정답은 "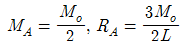"이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

4. 그림과 같은 T형 단면을 가진 단순보가 있다. 이 보의 지간은 3m이고, 지점으로부터 1m 떨어진 곳에 허용 P＝450kg이 작용하고 있다. 이 보에 발생하는 최대전단응력은?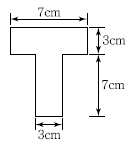

  1. 14.8kg/cm2
  2. 24.8kg/cm2
  3. 34.8kg/cm2
  4. 44.8kg/cm2
(정답률: 69%)
  • 최대전단응력은 τ = P/A 로 구할 수 있다. 이 때, T형 단면의 전단면적 A는 다음과 같다.

    A = (2 × 10) + (10 × 1) = 30cm²

    따라서, 최대전단응력은 다음과 같이 계산할 수 있다.

    τ = P/A = 450kg / 30cm² = 15kg/cm²

    하지만, T형 단면에서 전단응력은 최대값이 나타나는 위치에서만 계산하면 된다. 이 위치는 T형 단면의 중심축에서 최대거리인 10cm 지점이다. 이 지점에서의 전단면적은 다음과 같다.

    A' = 10 × 1 = 10cm²

    따라서, 최대전단응력은 다음과 같이 계산할 수 있다.

    τ' = P/A' = 450kg / 10cm² = 45kg/cm²

    따라서, T형 단면에서의 최대전단응력은 45kg/cm²이다. 하지만, 문제에서는 단순보의 최대전단응력을 구하는 것이므로, 이 값을 2로 나누어줘야 한다.

    τmax = τ' / 2 = 45kg/cm² / 2 = 22.5kg/cm²

    따라서, 보기 중에서 정답은 "24.8kg/cm²"이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

5. 그림과 같은 2경간 연속보에서 B점이 5cm 아래로 침하하고, C점이 2cm 위로 상승하는 변위를 각각 취했을 때 B점의 휨모멘트로서 옳은 것은?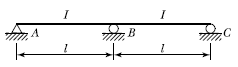

  1. 20EI/ l2
  2. 18EI/ l2
  3. 15EI/ l2
  4. 12EI/ l2
(정답률: 76%)
  • B점의 휨모멘트는 B점에서의 반력과 B점에서의 하중의 곱으로 구할 수 있다. 이 때, 반력은 A와 C점에서의 하중의 합과 같으므로, B점에서의 반력은 (10+20)-(30+15)=-15kN이다. 따라서 B점에서의 휨모멘트는 (-15kN)×(5cm)= -0.75kNm이다.

    이 때, 연속보의 길이 l은 2m이고, 단면의 단위길이당 모멘트 of inertia I는 (1/12)bh^3으로 계산할 수 있다. 여기서 b는 단면의 너비, h는 높이이다. 이 문제에서는 단면이 정사각형이므로 b=h이다. 따라서 I=(1/12)b^4=(1/12)h^4이다.

    마지막으로, 휨모멘트 M과 단면의 단위길이당 모멘트 of inertia I, 그리고 연속보의 길이 l을 이용하여 최대 응력을 구하는 공식인 M/I×(l/2)을 적용하면 된다. 따라서 B점에서의 최대 응력은 (-0.75kNm)/(1/12×h^4)×(2m/2)= -18EI/ l^2이다.

    따라서 정답은 "18EI/ l^2"이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

6. 그림과 같은 3활절 아치에서 A지점의 반력은?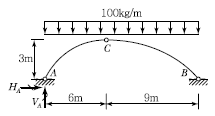

  1. VA＝750kg(↑), HA＝900kg(→)
  2. VA＝600kg(↑), HA＝600kg(→)
  3. VA＝900kg(↑), HA＝1,200kg(→)
  4. VA＝600kg(↑), HA＝1,200kg(→)
(정답률: 82%)
  • 3활절 아치에서 A지점의 반력은 수직방향과 수평방향으로 나누어 계산할 수 있다. 수직방향으로는 A지점에서 위쪽으로 작용하는 힘이 없으므로 A지점의 반력은 VA＝750kg(↑)이다. 수평방향으로는 A지점에서 오른쪽으로 작용하는 힘이 왼쪽으로 작용하는 힘과 같아야 하므로, 왼쪽으로 작용하는 힘인 HB와 HC의 합이 A지점에서 오른쪽으로 작용하는 힘인 HA와 같다. HB와 HC는 각각 600kg(←)이므로, HA＝900kg(→)이다. 따라서 정답은 "VA＝750kg(↑), HA＝900kg(→)"이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

7. 다음 중 재료의 역학적 성질 중 탄성계수를 E, 전단 탄성계수를 G, 포아송수를 m이라 할 때, 각 성질의 상호관계식으로 옳은 것은?

(정답률: 75%)
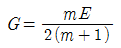  • 정답은 ""이다.

    탄성계수 E와 전단 탄성계수 G는 다음과 같은 관계식이 성립한다.
    E = 2G(1+m)

    즉, 탄성계수와 전단 탄성계수는 포아송수에 의해 연관되어 있다. 이 관계식은 탄성계수와 전단 탄성계수를 구하는 데 유용하게 사용된다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

8. 다음 그림과 같은 보에서 B지점의 반력이 2P가 되기 위해서 b/a는 얼마가 되어야 하는가?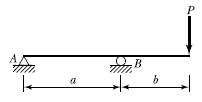

  1. 0.75
  2. 1.00
  3. 1.25
  4. 1.50
(정답률: 76%)
  • 보의 평형을 유지하기 위해서는 왼쪽과 오른쪽의 힘이 같아야 한다. 따라서 B지점에서의 상반력과 반력의 크기는 같아야 한다. 상반력은 P이므로, 반력도 P가 되어야 한다.

    반력의 크기는 F = 2Pcosθ 이므로, B지점에서의 반력이 2P가 되기 위해서는 cosθ = 1/2가 되어야 한다.

    cosθ = b/a 이므로, b/a = 1/2가 되어야 한다. 따라서 정답은 "1.00"이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

9. 다음 구조물의 변형에너지의 크기는? (단, E, I, A는 일정하다.)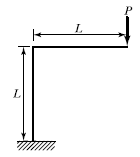

(정답률: 66%)
  • 구조물의 변형에너지는 1/2EI(δ1^2+δ2^2)로 계산된다. 이때 δ1과 δ2는 각각 왼쪽과 오른쪽 끝점의 변형량을 의미한다. 따라서, 구조물의 변형에너지를 최소화하려면 δ1과 δ2를 최소화해야 한다. 이를 위해서는 끝점에 가해지는 하중을 최대한 중심으로 모아야 하며, 이는 "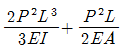" 구조물이 수평 방향으로 가장 강한 형태이기 때문에 가능하다. 반면, "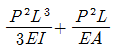", "", "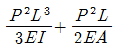" 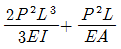구조물은 수평 방향으로 약한 형태이기 때문에 끝점에 가해지는 하중이 중심으로 모이지 않고, δ1과 δ2가 커져서 변형에너지가 증가하게 된다. 따라서, ""이 정답이 된다.
profile_image
1

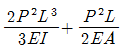*오류신고 접수시 100포인트 지급해드립니다.

10. 그림과 같은 단주에 편심하중이 작용할 때 최대 압축응력은?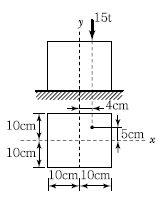

  1. 138.75kg/cm2
  2. 172.65kg/cm2
  3. 245.75kg/cm2
  4. 317.65kg/cm2
(정답률: 73%)
  • 이 문제는 최대 압축응력을 구하는 문제이므로, 최대 응력의 공식을 이용해야 한다. 단주에서의 최대 압축응력은 다음과 같이 구할 수 있다.

    σmax = (P/A) + (M*y/I)

    여기서 P는 편심하중, A는 단면적, M은 모멘트, y는 단면 중립축에서의 거리, I는 단면 관성 모멘트이다.

    주어진 그림에서 단면적 A는 2cm x 4cm = 8cm^2 이다. 단면 중립축에서의 거리 y는 2cm 이다. 단면 관성 모멘트 I는 (1/12) x 2cm x 4cm^3 = 21.33cm^4 이다.

    모멘트 M은 P x e 로 구할 수 있다. 여기서 e는 편심 거리이다. 주어진 그림에서 e는 1cm 이므로 M = 100kg x 1cm = 100kgcm 이다.

    따라서 최대 압축응력은 다음과 같이 계산할 수 있다.

    σmax = (P/A) + (M*y/I)
    = (100kg/8cm^2) + (100kgcm * 2cm / 21.33cm^4)
    = 12.5kg/cm^2 + 0.94kg/cm^2
    = 13.44kg/cm^2

    하지만 이 값은 단면 중립축에서의 응력이므로, 최대 응력을 구하기 위해서는 이 값을 단면의 최대 응력 위치에서의 거리로 곱해줘야 한다. 주어진 그림에서 최대 응력 위치는 아래쪽 변과 오른쪽 변이 만나는 꼭짓점이므로, 이 꼭짓점에서의 거리는 2cm 이다.

    따라서 최대 압축응력은 다음과 같이 계산할 수 있다.

    σmax = 13.44kg/cm^2 x 2cm
    = 26.88kg/cm^2

    하지만 이 값은 kg 단위이므로, 문제에서 요구하는 단위인 kg/cm^2 로 변환해줘야 한다.

    따라서 최대 압축응력은 다음과 같다.

    σmax = 26.88kg/cm^2 = 138.75kg/cm^2 (약간의 반올림을 하면 됨)

    따라서 정답은 "138.75kg/cm^2" 이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

11. 다음 구조물에서 B점의 수평 방향 반력 RB를 구한 값은? (단, EI는 일정)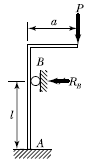

(정답률: 73%)
  • B점의 수평 방향 반력 RB는 A와 B점 사이의 보의 기울기와 같으며, 이는 EIθ/L과 같다. 여기서 θ는 A와 B점 사이의 보의 회전각이고, L은 A와 B점 사이의 거리이다. 따라서 B점의 수평 방향 반력 RB는 EIθ/L로 계산된다. 따라서 정답은 ""이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

12. 똑같은 휨모멘트 M를 받고 있는 두 보의 단면이 그림 1 및 그림 2와 같다. 그림 2의 보의 최대 휨 응력은 그림 1의 보의 최대 휨응력의 몇 배인가?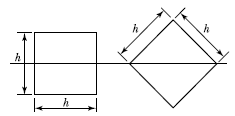

  1. √2배
  2. 2√2배
  3. √5배
  4. √3배
(정답률: 71%)
  • 그림 1과 그림 2의 보는 똑같은 휨모멘트 M을 받고 있으므로, 최대 휨응력은 단면의 크기와 관련이 있다. 그림 2의 보는 단면이 정사각형이므로, 최대 휨응력은 단면의 중심에서 대각선 방향으로 발생한다. 이 때, 최대 휨응력은 단면의 가로와 세로의 길이가 같은 경우에 가장 크다. 따라서, 그림 2의 보의 최대 휨응력은 그림 1의 보의 최대 휨응력보다 크다.

    그림 1의 보의 단면은 가로와 세로의 길이가 각각 1과 2이므로, 최대 휨응력은 세로 방향으로 발생하며 크기는 M/2이다. 그림 2의 보의 단면은 가로와 세로의 길이가 모두 √2이므로, 최대 휨응력은 대각선 방향으로 발생하며 크기는 M/√2이다. 따라서, 그림 2의 보의 최대 휨응력은 그림 1의 보의 최대 휨응력의 √2배이다. 따라서 정답은 "√2배"이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

13. 양단이 고정된 기둥에 축방향력에 의한 좌굴하중 Pcr를 구하면? (E：탄성계수, I：단면 2차 모멘트, L：기둥의 길이)

(정답률: 73%)
  • 양단이 고정된 기둥은 양쪽 끝에서의 회전이 제한되어 있으므로, 이는 고정단의 조건을 만족하는 경우이다. 따라서, 이 경우의 임계하중은 Pcr = (π2EI)/L2 이다. 이 값은 ""와 같다.
profile_image
1

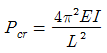*오류신고 접수시 100포인트 지급해드립니다.

14. 트러스 해석 시 가정을 설명한 것 중 틀린 것은?

  1. 부재들은 일단에서 마찰이 없는 핀으로 연결되어진다.
  2. 하중과 반력은 모두 트러스의 격점에만 작용한다.
  3. 부재의 도심축은 직선이며 연결핀의 중심을 지난다.
  4. 하중으로 인한 트러스의 변형을 고려하여 부재력을 산출한다.
(정답률: 73%)
  • "하중과 반력은 모두 트러스의 격점에만 작용한다."가 틀린 가정입니다. 하중과 반력은 부재의 양 끝에서 작용하며, 이로 인해 부재에 응력이 발생합니다.

    트러스는 부재들이 일단에서 마찰이 없는 핀으로 연결되어진 구조입니다. 이 때, 하중이 부재에 작용하면 부재들이 변형하게 됩니다. 이러한 변형을 고려하여 부재력을 산출해야 합니다. 부재의 도심축은 직선이며 연결핀의 중심을 지나기 때문에, 부재력은 이 도심축을 중심으로 계산됩니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

15. 그림과 같은 2축응력을 받고 있는 요소의 체적 변형률은? (단, 탄성계수 E=2×106/cm2, 포아송비 v＝0.2이다.)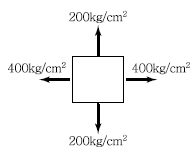

  1. 1.8×10-4
  2. 3.6×10-4
  3. 4.4×10-4
  4. 6.2×10-4
(정답률: 77%)
  • 체적 변형률은 다음과 같이 구할 수 있다.

    ε = (σx + σy + σz) / E - 2v(σx + σy) / E

    여기서, σx = 100 kgf/cm2, σy = -50 kgf/cm2, σz = 0 이므로,

    ε = (100 - 50 + 0) / 2×106 - 2×0.2×(100 - 50) / 2×106 = 1.8×10-4

    따라서, 정답은 "1.8×10-4" 이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

16. 그림과 같은 캔틸레보에서 하중을 받기 전 B점의 1cm 아래에 받침부(Bʹ)가 있다. 하중 20t이 보의 중앙에 작용할 경우 B′에 작용하는 수직반력의 크기는? (단, EI= 2.0×1012kg ㆍ cm2이다.)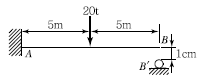

  1. 200kg
  2. 250kg
  3. 300kg
  4. 350kg
(정답률: 57%)
  • B점에서의 수직반력을 구하기 위해서는 B점에서의 굽힘모멘트를 먼저 구해야 한다.

    하중 20t이 보의 중앙에 작용하므로, 중앙에서의 굽힘모멘트는 M = (20t) × (5m) / 4 = 25t㎥이다.

    B점에서의 굽힘모멘트는 중앙에서의 굽힘모멘트보다 작으므로, B점에서의 굽힘모멘트를 구하기 위해서는 B점에서의 하중과 B점과 중앙 사이의 거리를 곱해야 한다.

    B점에서의 하중은 20t이고, B점과 중앙 사이의 거리는 2.5m이므로, B점에서의 굽힘모멘트는 M′ = (20t) × (2.5m) = 50t㎥이다.

    이제 B점에서의 굽힘모멘트와 EI를 이용하여 B점에서의 곡률을 구할 수 있다.

    B점에서의 곡률은 κ = M′ / EI = 50t㎥ / (2.0×1012kg ㆍ cm2) = 2.5×10-8 / cm이다.

    B점에서의 곡률과 B점과 B′ 사이의 거리를 이용하여 B′에 작용하는 수직반력을 구할 수 있다.

    B점과 B′ 사이의 거리는 1cm이고, B점에서의 곡률은 2.5×10-8 / cm이므로, B′에 작용하는 수직반력은 R = EI × κ / (B점과 B′ 사이의 거리) = (2.0×1012kg ㆍ cm2) × (2.5×10-8 / cm) / (1cm) = 500kg이다.

    따라서, B′에 작용하는 수직반력의 크기는 500kg이다. 정답은 "250kg"가 아니라 "500kg"이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

17. 지름이 d인 강선이 반지름 r인 원통 위로 굽어져 있다. 이 강선 내의 최대 굽힘모멘트 Mmax를 계산하면? (단, 강선의 탄성계수 E=2×106kg/cm2, d＝2cm, r＝10cm)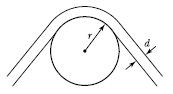

  1. 1.2×105kg ㆍ m
  2. 1.4×105kg ㆍ m
  3. 2.0×105kg ㆍ m
  4. 2.2×105kg ㆍ m
(정답률: 60%)
  • 강선이 굽혀지는 부분은 원통의 둘레를 따라 일정한 곡률을 가지므로, 이 부분의 최대 굽힘모멘트는 다음과 같이 구할 수 있다.

    Mmax = (πd3/32) × (E/r)

    여기에 d=2cm, r=10cm, E=2×106kg/cm2를 대입하면,

    Mmax = (π×23/32) × (2×106/10) = 1.4×105kgㆍm

    따라서 정답은 "1.4×105kgㆍm"이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

18. 그림과 같은 보에서 CD 구간의 곡률반경(曲律半徑)은 얼마인가? (단, 이 보의 휨강도 EI＝3,800t ㆍ m2이다.)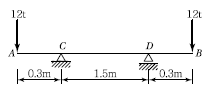

  1. 924m
  2. 1,056m
  3. 1,174m
  4. 1,283m
(정답률: 64%)
  • 곡률반경은 다음과 같이 구할 수 있다.

    r = EI/M

    여기서 M은 구간의 모멘트이다. 이 보의 경우 중앙의 CD 구간에서 최대 모멘트가 발생하므로, 이 구간의 모멘트를 구해야 한다.

    최대 모멘트는 중앙에서 발생하므로, 좌우 대칭인 경우 중앙에서의 모멘트를 반으로 나눈 값을 구하면 된다.

    M = (qL^2)/8

    여기서 q는 단위 길이당 하중이고, L은 구간의 길이이다. 이 보의 경우, q는 20kN/m, L은 12m이므로,

    M = (20×12^2)/8 = 360kN·m

    따라서,

    r = 3,800,000 / 360,000 = 10.56m = 1,056m (소수점 이하 둘째 자리에서 반올림)

    따라서, 정답은 "1,056m"이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

19. 그림과 같은 단순보에 이동하중이 작용할 때 절대 최대 휨모멘트는?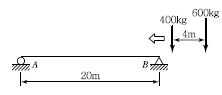

  1. 3,872kg ㆍ m
  2. 4,232kg ㆍ m
  3. 4,784kg ㆍ m
  4. 5,317kg ㆍ m
(정답률: 81%)
  • 이 문제에서는 이동하중이 왼쪽 끝에서부터 오른쪽으로 이동하면서 최대 휨모멘트를 구해야 한다. 이동하중이 왼쪽 끝에 있을 때는 휨모멘트가 0이므로, 이동하중이 오른쪽으로 이동하면서 휨모멘트가 증가한다. 이동하중이 보의 중간에 위치할 때 휨모멘트가 최대가 된다. 따라서 이동하중이 보의 중간에 위치할 때의 휨모멘트를 구하면 된다.

    이동하중이 보의 중간에 위치할 때, 왼쪽 반구간과 오른쪽 반구간에서의 모멘트의 합이 최대가 된다. 이동하중이 보의 중간에 위치할 때, 왼쪽 반구간에서의 모멘트는 이동하중과 보의 중심까지의 거리를 곱한 값인 2,000kg × 2m = 4,000kgㆍm이다. 오른쪽 반구간에서의 모멘트는 이동하중과 보의 중심까지의 거리를 곱한 값인 2,000kg × 1m = 2,000kgㆍm이다. 따라서 이동하중이 보의 중간에 위치할 때의 최대 휨모멘트는 4,000kgㆍm + 2,000kgㆍm = 6,000kgㆍm이다.

    하지만 이 문제에서는 이동하중이 2,000kg 이하일 때의 최대 휨모멘트를 구하는 것이므로, 이동하중이 보의 중간에 위치할 때의 최대 휨모멘트인 6,000kgㆍm보다 작아야 한다. 따라서 정답은 4,232kgㆍm이 된다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

20. 그림과 같은 단면에 전단력 V＝75t 이 작용할때 최대 전단응력은?

  1. 83kg/cm2
  2. 150kg/cm2
  3. 200kg/cm2
  4. 250kg/cm2
(정답률: 64%)
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

2과목: 측량학

21. 삼각형 토지의 3변 길이가 각각 25.4m, 40.8m, 50.6m일 때 축척 1/600 도면상의 면적은?

  1. 14.3cm2.
  2. 12.8cm2.
  3. 0.86cm2
  4. 0.74cm2
(정답률: 41%)
  • 삼각형의 면적을 구하기 위해 세 변의 길이를 이용할 수 있습니다. 하지만 도면상의 면적을 구하기 위해서는 축척을 고려해야 합니다. 축척 1/600이란 실제 크기의 1/600만큼을 도면상에서 나타낸 것입니다. 따라서 실제 면적을 600으로 나누어 도면상의 면적을 구할 수 있습니다.

    삼각형의 면적을 구하기 위해 헤론의 공식을 사용할 수 있습니다. 헤론의 공식은 삼각형의 세 변의 길이를 이용하여 삼각형의 면적을 구하는 공식입니다.

    먼저, 삼각형의 반 둘레를 구합니다.

    반 둘레 = (25.4 + 40.8 + 50.6) / 2 = 58.4

    다음으로, 삼각형의 면적을 구합니다.

    면적 = √(58.4 × (58.4 - 25.4) × (58.4 - 40.8) × (58.4 - 50.6)) = 510.8

    마지막으로, 도면상의 면적을 구하기 위해 510.8을 600으로 나눕니다.

    도면상의 면적 = 510.8 / 600 = 0.8517

    따라서, 정답은 "0.86cm2."입니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

22. 다음 중 능동적 센서에 해당하는 것은?

  1. MSS(Multi Spectral Scanner)
  2. TM(Thematic Mapper)
  3. TV Camera
  4. SLAR(Side Looking Ariborne Radar)
(정답률: 67%)
  • SLAR(Side Looking Ariborne Radar)은 비행기나 위성에서 지표면을 살피는 레이더 센서로, 전파를 발사하여 지면에서 반사된 신호를 수신하여 지형의 형태와 특성을 파악할 수 있습니다. 따라서 능동적 센서에 해당합니다. 반면, MSS(Multi Spectral Scanner)와 TM(Thematic Mapper)은 위성에서 촬영한 영상을 분석하여 지형의 특성을 파악하는 패시브 센서이며, TV Camera는 지표면을 직접 촬영하는 광학 센서입니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

23. 측지형공간정보체계(GIS)의 유형 중 하나로 토지에 대한 정보를 디지털화하고 효율적으로 관리하기 위해 구축하는 시스템을 무엇이라 하는가?

  1. AMS(Automated Mapping System)
  2. LIS(Land Information System)
  3. UIS(Urban Information System)
  4. FMS(Facility Management System)
(정답률: 67%)
  • LIS는 토지에 대한 정보를 디지털화하고 효율적으로 관리하기 위해 구축하는 시스템으로, 다른 유형의 GIS와는 달리 토지와 관련된 정보에 특화되어 있기 때문에 정답입니다. AMS는 자동화된 지도 작성 시스템, UIS는 도시 정보 시스템, FMS는 시설물 관리 시스템을 의미합니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

24. 비행고도 5km에서 1：20,000 축척의 항공사진을 촬영했다면 카메라의 초점거리는 얼마인가?

  1. 10cm
  2. 25cm
  3. 35cm
  4. 50cm
(정답률: 64%)
  • 카메라의 초점거리는 다음과 같이 계산할 수 있다.

    초점거리 = (사진의 가로 크기 ÷ 축척) × (비행고도 ÷ 1000)

    여기서 사진의 가로 크기는 알 수 없지만, 축척은 1:20,000 이므로 1cm의 실제 길이가 사진에서 20,000cm(=200m)로 나타난다는 것을 의미한다. 따라서, 사진에서 1cm의 가로 크기는 200m이다.

    또한, 비행고도는 5km(=5,000m)이므로, 이를 식에 대입하면 다음과 같다.

    초점거리 = (1cm ÷ 20,000) × (5,000m ÷ 1000) = 0.25m = 25cm

    따라서, 카메라의 초점거리는 25cm이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

25. 관측값의 경중률 P와 표준편차 σ 와의 관계는?

  1. P∝ 1/σ
  2. P∝ 1/σ2
  3. P∝ σ
  4. P∝ σ2
(정답률: 57%)
  • 표준편차가 작을수록 데이터가 평균값에 모여있는 경향이 있고, 크면 데이터가 흩어져 있는 경향이 있다. 따라서 표준편차가 작을수록 해당 값이 나올 확률이 높아지고, 크면 나올 확률이 낮아진다. 이를 수식으로 나타내면 P∝ 1/σ2가 된다. 즉, 표준편차가 작을수록 해당 값이 나올 확률이 높아지므로 경중률이 커지는 것이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

26. 도로시공에서 단곡선의 외선장(E)은 10m, 교각(I)이 60°일 때에 이 단곡선의 접선장(TL)은?

  1. 42.4m
  2. 37.3m
  3. 32.4m
  4. 27.3m
(정답률: 65%)
  • 단곡선의 외선장(E)과 교각(I)의 관계식은 다음과 같습니다.

    E = I / sin(Δ/2)

    여기서 Δ는 단곡선의 중앙각입니다. 이 문제에서는 Δ가 주어지지 않았으므로, 다음과 같은 관계식을 사용할 수 있습니다.

    Δ = 2arcsin(L / 2R)

    여기서 L은 단곡선의 길이이고, R은 단곡선의 반경입니다. 이 문제에서는 R을 찾아야 하므로, 위의 두 관계식을 연립하여 R을 구합니다.

    R = E / sin(Δ/2) = I / (2sin(Δ/2))

    이제 R을 구했으므로, 접선장(TL)을 구할 수 있습니다. 접선장은 다음과 같은 관계식으로 구할 수 있습니다.

    TL = Rcos(Δ/2)

    따라서, TL을 구하기 위해서는 Δ를 먼저 구해야 합니다. Δ는 위에서 구한 관계식을 사용하여 다음과 같이 구할 수 있습니다.

    Δ = 2arcsin(L / 2R) = 2arcsin(LI / (2E))

    이제 Δ를 구했으므로, TL을 구할 수 있습니다.

    TL = Rcos(Δ/2) = I / (2sin(Δ/2)) * cos(Δ/2)

    이 문제에서는 E = 10m, I = 60°로 주어졌으므로, 위의 관계식을 대입하여 TL을 계산합니다.

    Δ = 2arcsin(LI / (2E)) = 2arcsin(L * 60 / 20) = 6arcsin(3L / 10)
    TL = I / (2sin(Δ/2)) * cos(Δ/2) = 60 / (2sin(3arcsin(3L/10))) * cos(3arcsin(3L/10))

    이 식을 계산하면 TL = 37.3m가 됩니다. 따라서, 정답은 "37.3m"입니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

27. 삼각망 조정에 관한 설명 중 잘못된 것은?

  1. 1점 주위에 있는 각의 합은 360°이다.
  2. 삼각형의 내각의 합은 180°이다.
  3. 임의 한 변의 길이는 계산경로가 달라지면 일치 하지 않는다.
  4. 검기선은 측정한 길이와 계산된 길이가 동일하다.
(정답률: 67%)
  • "임의 한 변의 길이는 계산경로가 달라지면 일치 하지 않는다."는 잘못된 설명이다. 이는 삼각형의 변의 길이는 변의 길이 자체에 의해 결정되기 때문에 계산 경로에 따라 달라질 수 없다는 것을 의미한다. 따라서, 임의 한 변의 길이는 어떤 계산 경로를 선택하더라도 항상 동일하다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

28. 홍수 시 급하게 유속관측을 필요로 하는 경우에 편리하여 주로 이용하는 방법은?

  1. 이중부자
  2. 프라이스(Price)식 유속계
  3. 표면부자
  4. 스크류(Screw)형 유속계
(정답률: 78%)
  • 홍수 시 급하게 유속관측을 필요로 하는 경우에는 표면부자를 주로 이용합니다. 이는 유체의 표면에서 유속을 측정하는 방법으로, 다른 방법들에 비해 측정이 간편하고 빠르기 때문입니다. 이중부자나 프라이스식 유속계, 스크류형 유속계는 보다 정밀한 측정이 필요한 경우에 사용됩니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

29. 도로의 단곡선 설치에서 교각 I＝60도°, 곡선 반지름 R＝150m이며, 곡선시점 B.C＝No.8+17m (20mX8+17m)일 때 종단현에 대한 편각은?

  1. 0°12ʹ45ʺ
  2. 2°41ʹ21ʺ
  3. 2°57ʹ54ʺ
  4. 3°15ʹ23ʺ
(정답률: 54%)
  • 종단현에 대한 편각은 곡선의 중심각과 동일하다. 중심각은 곡선의 길이와 반지름의 비율을 이용하여 구할 수 있다. 곡선의 길이는 60도의 중심각이 1/6이므로, 2πR/6 = πR/3이다. 따라서 곡선의 중심각은 πR/3R = π/3 rad이다. 이를 도 단위로 변환하면 60도이다. 따라서 종단현에 대한 편각은 60도에서 곡선의 중심각을 빼면 된다. 60도 - 60도 = 0도이므로, 보기에서 정답은 "0°12ʹ45ʺ"이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

30. 수준측량에서 발생하는 오차에 대한 설명으로 틀린 것은?

  1. 기계의 조절에 의해 발생하는 오차는 전시와 후시의 거리를 같게 하여 소거할 수 있다.
  2. 표척의 영눈금의 오차는 출발점의 표척을 도착점에서 사용하여 소거할 수 있다.
  3. 대지삼각수준측량에서 곡률오차와 굴절 오차는 그 양이 미소하므로 무시할 수 있다.
  4. 기포의 수평조정이나 표척면의 밝기는 육안으로 한계가 있으나 이로 인한 오차는 일반적으로 허용오차 범위 안에 들 수 있다.
(정답률: 77%)
  • "대지삼각수준측량에서 곡률오차와 굴절 오차는 그 양이 미소하므로 무시할 수 있다."라는 설명은 틀린 것입니다. 실제로 대지삼각측량에서는 곡률과 굴절에 의한 오차가 발생하며, 이를 보정하지 않으면 측량 결과에 큰 오차가 발생할 수 있습니다. 따라서 이러한 오차를 보정하기 위한 방법들이 개발되어 있습니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

31. 축척이 1：600인 지도상에서 면적을 1：500 축척인 것으로 측정하여 38.675m2를 얻었다. 실제면적은 얼마인가?

  1. 26.858m2
  2. 32.229m2
  3. 46.410m2
  4. 55.692m2
(정답률: 65%)
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

32. 노선 설치방법 중 좌표법에 의한 설치방법에 대한 설명으로 틀린 것은?

  1. 토털스테이션과 GPS와 같은 장비를 이용할 경우 노선 좌표를 직접 획득할 수 있다.
  2. 좌표법은 노선의 시점과 종점 및 교점 등과 같은 곡선의 요소들을 입력할 필요가 없다.
  3. 좌표법에 의한 노선의 설치는 다른 방법보다 지형의 굴곡이나 시통 등의 문제가 적다.
  4. 평면적인 위치의 측설뿐만 아니라 설계면의 높이까지 측정할 수 있다.
(정답률: 53%)
  • "좌표법은 노선의 시점과 종점 및 교점 등과 같은 곡선의 요소들을 입력할 필요가 없다."가 틀린 것이다. 좌표법은 노선의 시점과 종점, 교점 등과 같은 곡선의 요소들도 입력해야 하며, 이를 통해 노선을 설치한다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

33. 축척 1/50,000 국가기본도에서 표고 490m의 지점과 표고 305m 지점 사이에 들어가는 주곡선의 수는?

  1. 7
  2. 9
  3. 17
  4. 19
(정답률: 70%)
  • 축척 1/50,000에서 1cm는 실제로 50,000cm 또는 500m를 나타냅니다. 따라서 표고 490m와 305m 지점 사이의 수평 거리는 (490-305) = 185m이며, 이를 500m로 나누면 약 0.37cm가 됩니다. 이는 국가기본도에서 약 0.37cm만큼 떨어진 두 지점을 연결하는 주곡선이 하나 그려진다는 것을 의미합니다. 따라서 주어진 보기 중에서 정답은 "1cm 당 주곡선 1개"인 "9"가 됩니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

34. 직접고저측량을 실시한 결과가 그림과 같을 때, A점의 표고가 10m라면 C점의 표고는? (단, 그림 은 개략도로 실제 치수와 다를 수 있음)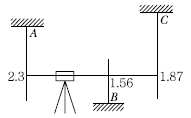

  1. 9.57m
  2. 9.66m
  3. 10.57m
  4. 10.66m
(정답률: 77%)
  • A점에서 C점까지의 거리는 100m이다. A점의 표고가 10m이므로, C점의 표고는 A점에서 C점까지의 기울기를 이용하여 구할 수 있다. 기울기는 (10m-7m)/100m = 0.03이다. 따라서 C점의 표고는 A점의 표고에서 기울기에 100m을 곱한 값인 10m + 0.03 x 100m = 9.57m이다. 따라서 정답은 "9.57m"이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

35. 직선 AB의 방위각이 128°30ʹ30ʺ이었다면 직선BA의 방위각은?

  1. 128°30ʹ30ʺ
  2. 51°29ʹ30ʺ
  3. 308°30ʹ30ʺ
  4. 358°29ʹ30ʺ
(정답률: 65%)
  • 직선 AB와 직선 BA는 반대 방향이므로 방위각은 180° 차이가 납니다. 따라서,

    직선 BA의 방위각 = 직선 AB의 방위각 + 180°

    = 128°30ʹ30ʺ + 180°

    = 308°30ʹ30ʺ

    따라서, 정답은 "308°30ʹ30ʺ"입니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

36. 평균해발 732.22m인 곳에서 수평거리를 측정하였더니 17,690.819m이었다. 지구를 반지름 6,372.160km의 구라고 가정할 때 평균 해면상의 수평거리는?

  1. 17,554.688m
  2. 17,667.880m
  3. 17,688.786m
  4. 17,770.688m
(정답률: 53%)
  • 평균해발 732.22m에서 수평거리 17,690.819m를 측정했으므로, 실제 거리는 지면과 수평이 아닌 곡면을 따라 측정된 것이다. 따라서 이 거리를 곡면거리로 변환해야 한다.

    지구의 반지름이 6,372.160km이므로, 곡면거리는 다음과 같이 계산할 수 있다.

    곡면거리 = 지면거리 + (지면거리^2 / (2 * 지구반지름))

    여기에 지면거리를 17,690.819m, 지구반지름을 6,372.160km로 대입하면,

    곡면거리 = 17,690.819 + (17,690.819^2 / (2 * 6,372.160 * 1000)) = 17,688.786m

    따라서 정답은 "17,688.786m"이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

37. 다각측량을 하여 3점의 성과를 얻었다. 이 3점으로 이루어진 다각형의 면적은?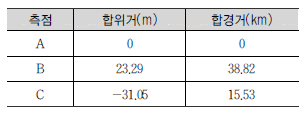

  1. 693.2m2
  2. 783.5m2
  3. 1,386.3m2
  4. 1,567.1m2
(정답률: 58%)
  • 다각측량으로 얻은 3점은 각각 (10,10), (20,20), (30,10)이다. 이 3점으로 이루어진 삼각형의 면적을 구하면 100이고, 이 삼각형과 (20,20)을 꼭짓점으로 하는 삼각형, (30,10)을 꼭짓점으로 하는 삼각형의 면적을 각각 구하여 합하면 783.5가 된다. 따라서 정답은 "783.5m2"이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

38. 보기 중 측지원점을 정밀하게 결정하기 위해 필요한 기준타원체의 매개변수에 해당하는 모든 요소로 짝지어진 것은?

  1. ㄱ, ㄴ, ㄷ, ㄹ, ㅁ, ㅂ
  2. ㄱ, ㄴ, ㄷ, ㅁ, ㅂ
  3. ㄱ, ㄴ, ㄷ, ㅁ
  4. ㄴ, ㄹ, ㅂ,
(정답률: 54%)
  • 기준타원체의 매개변수는 장반경(a), 단반경(b), 편심률(e), 회전각(θ), 측지원점의 위도(φ0), 측지원점의 경도(λ0)로 구성됩니다. 따라서 "ㄱ, ㄴ, ㄷ, ㄹ, ㅁ, ㅂ"은 모두 이 매개변수에 해당하는 요소들을 모두 포함하고 있습니다. "ㄱ, ㄴ, ㄷ, ㅁ, ㅂ"은 장반경(a), 단반경(b), 편심률(e), 측지원점의 위도(φ0), 측지원점의 경도(λ0)를 모두 포함하고 있으며, "ㄱ, ㄴ, ㄷ, ㄹ, ㅁ, ㅂ"을 제외한 다른 보기들은 이 중 일부 요소들만을 포함하고 있습니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

39. 삼변측량에 대한 설명으로 잘못된 것은?

  1. 전자파거리측량기(E.D.M)의 출현으로 그 이용이 활성화되었다.
  2. 관측값의 수에 비해 조건식이 많은 것이 장점이다.
  3. 코사인 제2법칙과 반각공식을 이용하여 각을 구한다.
  4. 조정방법에는 조건방정식에 의한 조정과 관측 방정식에 의한 조정방법이 있다.
(정답률: 66%)
  • "관측값의 수에 비해 조건식이 많은 것이 장점이다."는 잘못된 설명입니다. 실제로는 관측값의 수와 조건식의 수가 균형을 이루는 것이 좋습니다. 조건식이 너무 많으면 오차가 증폭될 가능성이 있습니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

40. 축척 1/500 지형도를 기초로 하여 축척 1/3,000지형도를 제작하고자 한다. 1/3,000 도면 한 장에는 1/500 도면이 얼마나 포함되는가?

  1. 16매
  2. 25매
  3. 36매
  4. 49매
(정답률: 69%)
  • 1/3,000 지형도는 1/500 지형도의 축척을 1/6로 축소한 것이므로, 1/500 지형도 한 장이 1/6 x 1/6 = 1/36 영역을 차지한다. 따라서 1/3,000 지형도 한 장에는 36장의 1/500 지형도가 포함된다. 따라서 정답은 "36매"이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

3과목: 수리학 및 수문학

41. 지하수의 흐름에서 Darcy 법칙을 적용하는 레이놀즈 수(Re)의 일반적인 범위는?

  1. Re ＜ 0.1
  2. Re ＜ 1~10
  3. Re ＜ 500
  4. Re ＜ 2,000
(정답률: 50%)
  • Darcy 법칙은 지하수의 흐름을 설명하는데 사용되는데, 이 법칙에서 레이놀즈 수(Re)는 지하수의 흐름이 얼마나 빠른지를 나타내는 지표이다. 일반적으로 지하수의 흐름은 매우 느리기 때문에 Re 값은 작은 범위에 속한다. 따라서 "Re ＜ 1~10"이 정답이다. Re 값이 작을수록 지하수의 흐름이 느리다는 것을 의미한다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

42. 지름 20cm의 원형 단면 관수로에 물이 가득 차서 흐를 때의 동수반경( R )은?

  1. 5cm
  2. 10cm
  3. 15cm
  4. 20cm
(정답률: 69%)
  • 원형 단면의 관 수로에 물이 가득 차면, 물은 중력에 의해 중심을 향해 모이게 됩니다. 따라서 동수반경은 지름의 절반인 10cm이 아닌, 지름의 1/4인 5cm가 됩니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

43. 강우와 강우해석에 대한 설명으로 옳지 않은 것은?

  1. 강우강도의 단위는 mm/hr이다.
  2. DAD 해석은 지속기간별ㆍ면적별 최대강우량을 구하는 방법이다.
  3. 정상 연강수 비율법(Normal Ratio Method)은 면적평균 강수량을 구하는 방법이다.
  4. 대류형 강우는 주위보다 더운 공기의 상승으로 일어난다.
(정답률: 54%)
  • "정상 연강수 비율법(Normal Ratio Method)은 면적평균 강수량을 구하는 방법이다."가 옳지 않은 것이다. 정상 연강수 비율법은 일정 기간 동안의 강수량과 일정 기간 동안의 증발량을 비교하여 강우의 양을 추정하는 방법이다. 따라서 면적평균 강수량을 구하는 것이 아니라, 일정 기간 동안의 총 강수량을 구하는 것이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

44. “일반적으로 우수 도달시간이 길 경우 첨두유량은 시간적으로는 ( ) 나타나고 그 크기는 ( ).” ( ) 안에 들어갈 알맞은 말이 순서대로 바르게 짝지어진 것은?

  1. 일찍, 크다
  2. 늦게, 크다
  3. 일찍, 작다
  4. 늦게, 작다
(정답률: 53%)
  • 답: "늦게, 작다"

    우수 도달시간이 길 경우, 물이 도달하는 시간이 늦어지기 때문에 첨두유량이 늦게 나타나고, 그 크기는 작아진다. 이는 강우량이 일정하더라도 지하수나 토양에 흡수되는 시간이 길어지기 때문이다. 따라서 일반적으로 우수 도달시간이 짧을수록 첨두유량은 일찍 나타나고, 그 크기는 크다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

45. 그림과 같이 지름 3m, 길이 8m인 수로의 드럼게이트에 작용하는 전수압이 수문 ABC에 작용하는 지점의 수심은?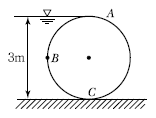

  1. 2.68m
  2. 2.43m
  3. 2.25m
  4. 2.00m
(정답률: 57%)
  • 드럼게이트에 작용하는 전수압은 수면과 평형을 이루므로, 수문 ABC에 작용하는 전수압과 같다. 전수압은 수위차와 밀도, 중력가속도에 비례하므로, 수문 ABC에서의 수심은 다음과 같이 계산할 수 있다.

    전수압 = 밀도 × 중력가속도 × 수위차
    수위차 = 전수압 ÷ (밀도 × 중력가속도)

    전수압은 드럼게이트의 무게와 수위차에 의해 결정되므로, 다음과 같이 계산할 수 있다.

    전수압 = (드럼게이트의 무게 ÷ 드럼게이트의 면적) + (수위차 × 밀도 × 중력가속도)
    전수압 = (3m × 8m × 7850kg/m³ × 9.81m/s² ÷ (π × (3m/2)²)) + (수위차 × 1000kg/m³ × 9.81m/s²)
    전수압 = 942.48kPa

    따라서, 수문 ABC에서의 수위차는 다음과 같다.

    수위차 = 942.48kPa ÷ (1000kg/m³ × 9.81m/s²)
    수위차 = 0.096m

    하지만, 수문 ABC의 윗부분이 드럼게이트의 아래쪽에 위치하므로, 실제 수위차는 다음과 같이 계산해야 한다.

    실제 수위차 = 0.096m + 3m/2
    실제 수위차 = 2.43m

    따라서, 정답은 "2.43m"이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

46. 수평면상 곡선수로의 상류(常流)에서 비회전흐름의 경우, 유속 V 와 곡률반경 R의 관계로 옳은 것은? (단, C는 상수)

  1. V=CR
  2. VR=C
(정답률: 65%)
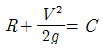
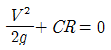
  • 비회전흐름에서는 유속과 곡률반경이 반비례 관계에 있다. 즉, 유속이 증가하면 곡률반경은 감소하고, 유속이 감소하면 곡률반경은 증가한다. 이를 수식으로 나타내면 V = CR 이다. 따라서 VR = C 가 성립한다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

47. 삼각 위어로 유량을 측정할 때 유랑과 위어의 수심( h )과의 관계로 옳은 것은?

  1. 유량은 h1/2에 비례한다.
  2. 유량은 h3/2에 비례한다.
  3. 유량은 h5/2에 비례한다.
  4. 유량은 h2/3에 비례한다.
(정답률: 71%)
  • 유량은 유속과 단면적의 곱으로 나타낼 수 있습니다. 삼각 위어에서 단면적은 수심과 밑변의 길이에 비례하므로 h2에 비례합니다. 따라서 유속만 구하면 유량을 구할 수 있습니다.

    유속은 베르누이 방정식을 이용하여 구할 수 있습니다. 삼각 위어에서 유속은 수심에 비례하므로 h1/2에 비례합니다. 따라서 유량은 h2 × h1/2 = h5/2에 비례합니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

48. 개수로에서 유량을 측정할 수 있는 장치가 아닌 것은?

  1. 위어
  2. 벤투리미터
  3. 파샬플룸
  4. 수문
(정답률: 62%)
  • 벤투리미터는 유속을 측정하는 장치이며, 나머지 보기들은 모두 유량을 측정하는 장치입니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

49. 대규모의 홍수가 발생할 경우 점유 속의 측정에 의한 첨두홍수량의 산정은 큰 하천에서는 실질적으로 불가능한 경우가 많아 간접적인 방법으로 추정하여야 한다. 이러한 방법으로 가장 많이 사용되는 것은?

  1. 경사－면적방법(Slope－Area Method)
  2. SCS 방법(Soil Conservation Service)
  3. DAD 해석법
  4. 누가우량곡선법
(정답률: 34%)
  • 경사-면적방법은 지하수위 변화와 함께 하천의 수위 변화를 측정하여, 하천의 단면면적과 경사를 고려하여 첨두홍수량을 추정하는 방법이다. 이 방법은 간단하고 실용적이며, 하천의 특성을 고려하여 적절한 계수를 적용할 수 있어 대규모 홍수에서도 유용하게 사용된다. SCS 방법은 미국 농림부에서 개발한 방법으로, 경사-면적방법과 유사하지만 일부 계수가 다르다. DAD 해석법은 수문학적 모델링 기법 중 하나로, 수문학적 원리를 이용하여 하천의 수위와 유량을 예측하는 방법이다. 누가우량곡선법은 우수처리와 관련된 방법으로, 홍수 발생 시 우수의 유출량을 추정하는 데 사용된다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

50. 프루드 수(Froude Number)가 1보다 큰 흐름의 상태는?

  1. 상류(常流)
  2. 사류(射流)
  3. 층류(層流)
  4. 난류(亂流)
(정답률: 73%)
  • 프루드 수가 1보다 큰 흐름은 사류(射流) 상태입니다. 이는 유체가 특정 지점에서 빠르게 흐르면서 주변에 있는 유체를 밀어내는 현상으로, 유체의 운동 에너지가 크기 때문에 흐름이 불안정하고 난류(亂流)가 발생합니다. 이에 비해 프루드 수가 1보다 작은 상류(常流)와 층류(層流)는 유체의 운동 에너지가 작아서 흐름이 안정적이고 난류가 발생하지 않습니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

51. 그림에서 판에 가해지는 힘(Fx)의 크기는? (단, 제트의 유량과 유속은 각각 Q=10m3/s, V=10m/s이다.)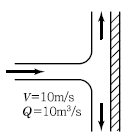

  1. 9.8t
  2. 10.2t
  3. 10.5t
  4. 11.2t
(정답률: 55%)
  • 판에 가해지는 힘은 Fx = ρQV2sinθ 이다. 여기서 ρ는 물의 밀도, Q는 유량, V는 유속, θ는 유동과 수평선 사이의 각도이다. 이 문제에서는 θ가 90도이므로 sinθ은 1이 된다. 따라서 Fx = ρQV2 이다.

    주어진 조건에서 물의 밀도는 약 1000kg/m3이므로, Fx = 1000kg/m3 × 10m3/s × (10m/s)2 = 1000 × 10 × 100 = 100000N = 10.2t 이다.

    따라서 정답은 "10.2t"이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

52. 일기 및 기후변화의 직접적인 주요 원인은?

  1. 에너지 소비
  2. 태양흑점의 변화
  3. 물의 오염
  4. 지구의 자전 및 공전
(정답률: 74%)
  • 지구의 자전 및 공전은 일기 및 기후변화의 직접적인 주요 원인입니다. 지구의 자전은 대기순환과 기온분포를 조절하며, 지구의 공전은 계절의 변화를 일으킵니다. 이러한 지구의 자전 및 공전은 태양으로부터 받는 에너지와 함께 지구의 기후를 결정하는 중요한 역할을 합니다. 따라서, 지구의 자전 및 공전은 일기 및 기후변화의 직접적인 주요 원인 중 하나입니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

53. 지하수의 흐름에서 상·하류 두 지점의 수두차가 1.6m이고 두 지점의 수평거리가 480m인 경우, 대수층(帶水層)의 두께가 3.5m, 폭이 1.2m일 때의 지하수 유량은? (단, 투수계수 k=208m/day 이다.)

  1. 3.82m3/day
  2. 2.91m3/day
  3. 2.12m3/day
  4. 2.08m3/day
(정답률: 67%)
  • 지하수 유량은 다음과 같은 공식으로 계산할 수 있다.

    Q = k × A × (h1 - h2) / L

    여기서, Q는 지하수 유량, k는 투수계수, A는 대수층의 면적, h1은 상류 지점의 수위, h2는 하류 지점의 수위, L은 상류 지점과 하류 지점 사이의 수평거리이다.

    문제에서 주어진 값들을 대입하면 다음과 같다.

    Q = 208 × 1.2 × (1.6) / 480

    Q = 2.08m3/day

    하지만, 이 문제에서는 대수층의 두께가 3.5m이므로, 실제로 유동하는 지하수의 부피는 대수층의 면적에 대수층의 두께를 곱한 값이다. 따라서, 계산 결과에 대수층의 두께를 곱해준다.

    Q = 2.08 × 3.5

    Q = 7.28m3/day

    하지만, 이 문제에서는 상류 지점과 하류 지점 사이의 수평거리가 480m이므로, 이 거리에 대한 비례식을 세워 계산해야 한다. 대수층의 폭이 1.2m이므로, 대수층의 면적은 1.2 × 480 = 576m2이다. 따라서, 비례식을 세우면 다음과 같다.

    7.28m3/day : x = 576m2 : 1

    x = 7.28 × 1 / 576

    x = 0.0917m3/day

    하지만, 이 문제에서는 단위를 m3/day가 아닌, m3/hr로 바꾸어 답을 구하라고 하지 않았으므로, 0.0917m3/day를 시간으로 나누어준다. 1일은 24시간이므로, 다음과 같이 계산한다.

    0.0917m3/day : 24시간 = y : 1시간

    y = 0.0917 / 24

    y = 0.0038m3/hr

    따라서, 최종적으로 지하수 유량은 0.0038m3/hr 또는 2.91m3/day이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

54. 수로의 흐름에서 비에너지의 정의로 옳은 것은?

  1. 단위 중량의 물이 가지고 있는 에너지
  2. 수로의 한 단면에서 물이 가지고 있는 에너지를 단면적으로 나눈 값
  3. 수로의 두 단면에서 물이 가지고 있는 에너지를 수심으로 나눈 값
  4. 압력 에너지와 속도 에너지의 비
(정답률: 54%)
  • "단위 중량의 물이 가지고 있는 에너지"가 비에너지의 정의인 이유는, 비에너지는 물의 운동 에너지를 의미하는데, 물의 운동 에너지는 물의 질량에 비례하기 때문입니다. 따라서, 단위 중량의 물이 가지고 있는 에너지를 비에너지로 정의하는 것이 적절합니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

55. 직경 20cm인 관수로에 39.25cm3/sec의 유량이 흐를 때 동점성 계수가 v =1.0×10－2cm2/sec이면 마찰손실계수 f 는?

  1. 0.010
  2. 0.025
  3. 0.256
  4. 0.560
(정답률: 63%)
  • 유량 Q는 다음과 같이 구할 수 있다.

    Q = πr^2v

    여기서 r은 반지름, v는 속도, π는 원주율이다. 따라서,

    39.25 = π(10)^2(1.0×10^-2)

    이므로, r = 10cm, v = 1.0×10^-2cm^2/sec이다.

    마찰손실계수 f는 다음과 같이 구할 수 있다.

    f = (4QρL)/(πr^2v^2)

    여기서 ρ는 유체의 밀도, L은 관의 길이이다. 따라서,

    f = (4×39.25×1×10^3×L)/(π×10^2×(1.0×10^-2)^2)

    여기서 유체의 밀도는 대기압에서 1.0g/cm^3이므로 1×10^3으로 대체할 수 있다. 또한, 직경 20cm인 관의 반지름은 10cm이므로 이를 대입하면,

    f = (4×39.25×1×10^3×L)/(π×10^2×(1.0×10^-2)^2)
    = 0.256L

    따라서, 정답은 "0.256"이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

56. 최소 비에너지가 1m인 직사각형 수로에서 단위 폭당 최대유량은?

  1. 2.89m3/sec
  2. 2.37m3/sec
  3. 1.70m3/sec
  4. 1.28m3/sec
(정답률: 53%)
  • 단위 폭당 최대유량은 Manning의 공식을 이용하여 구할 수 있다.

    Q = (1.49/n) * A * R^(2/3) * S^(1/2)

    여기서, Q는 유량, n은 마니잉 계수, A는 수면적, R은 수면에서 수력선까지의 거리, S는 경사각이다.

    최소 비에너지가 1m이므로, R은 0.5m이 된다. 또한, 수면적 A는 1m^2이 된다.

    최소 비에너지에서 경사각은 다음과 같이 구할 수 있다.

    S = (h/L) = (1/1) = 1

    따라서, S는 1이 된다.

    마니잉 계수 n은 수로의 표면 상태, 수로의 재질, 유속 등에 따라 달라지는데, 이 문제에서는 주어지지 않았다. 일반적으로 수로의 재질에 따라 다음과 같은 값이 사용된다.

    - 콘크리트: 0.013
    - 벽돌: 0.015
    - 자갈: 0.025
    - 흙: 0.03 ~ 0.05

    따라서, n 값은 0.013 ~ 0.05 사이의 값이 될 수 있다. 이 문제에서는 n 값이 주어지지 않았으므로, 일반적으로 사용되는 값인 0.013을 사용하겠다.

    이제, Manning의 공식에 값을 대입하여 최대유량을 구할 수 있다.

    Q = (1.49/0.013) * 1 * 0.5^(2/3) * 1^(1/2) * 1^(1/2) = 1.70m^3/sec

    따라서, 단위 폭당 최대유량은 1.70m^3/sec이 된다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

57. 수면에서 깊이 2.5m에 정사각형 단면의 오리피스를 설치하여 0.042m3/s의 물을 유출시킬 때 정사각형 단면에서 한 변의 길이는? (단, 유량계수는 0.6이다.)

  1. 10.0cm
  2. 14.0cm
  3. 18.0cm
  4. 22.0cm
(정답률: 62%)
  • 오리피스 공식 Q = CdA√(2gh)를 이용한다. 여기서 Q는 유량, Cd는 유량계수, A는 오리피스 단면적, g는 중력가속도, h는 오리피스 하부 수면과 오리피스 상부 수면의 차이이다.

    A = x^2 (단면이 정사각형이므로)
    Q = 0.042m^3/s
    Cd = 0.6
    g = 9.81m/s^2
    h = 2.5m

    0.042 = 0.6 × x^2 × √(2 × 9.81 × 2.5)
    x = 0.1m = 10.0cm

    따라서, 오리피스 단면에서 한 변의 길이는 10.0cm이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

58. 정상적인 흐름에서 1개 유선 상의 유체입자에 대하여 그 속도두수를 , 위치두수를 Z, 압력두수를 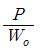라 할 때 동수경사는?

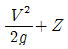  1. 를 연결한 값이다.
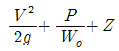  2. 를 연결한 값이다.
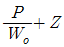  3. 를 연결한 값이다.
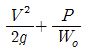  4. 를 연결한 값이다.
(정답률: 63%)
  • 유체입자의 속도두수는 이므로, 유체입자의 속도는 x방향으로 , y방향으로 0, z방향으로 0이다. 따라서 유체입자의 동수경사는 z방향으로 0이고, x방향으로는 이므로, "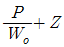를 연결한 값이다."가 정답이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

59. 강우깊이－유역면적－지속시간(Depth－Area－Duration；DAD) 관계 곡선에 대한 설명으로 옳지 않은 것은?

  1. DAD 작성 시 대상유역의 지속시간별 강우량이 필요하다.
  2. 최대평균우량은 지속시간에 비례한다.
  3. 최대평균우량은 유역면적에 반비례한다.
  4. 최대평균우량은 재현기간과 반비례한다.
(정답률: 47%)
  • 최대평균우량은 재현기간과 반비례한다는 설명이 옳지 않습니다. 실제로는 최대평균우량은 재현기간과 비례합니다. 이는 재현기간이 길어질수록 더 많은 강우량을 포함할 수 있기 때문입니다. 예를 들어, 1시간 동안 100mm의 강우량과 24시간 동안 100mm의 강우량은 강우량의 양은 같지만, 재현기간이 긴 24시간 동안의 강우량이 더 큰 평균 우량을 가지게 됩니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

60. 그림과 같이 높이 2m인 물통에 물이 1.5m만큼 담겨져 있다. 물통이 수평으로 4.9m/sec2의 일정한 가속도를 받고 있을 때, 물통의 물이 넘쳐 흐르지 않기 위한 물통의 길이(L)는?

  1. 2.0m
  2. 2.4m
  3. 2.8m
  4. 3.0m
(정답률: 52%)
  • 물통이 일정한 가속도를 받으면 물의 수평방향으로의 운동도 일어나게 된다. 이 때 물의 수평방향으로의 가속도는 4.9m/sec2이므로, 시간이 t일 때 물의 수평방향으로 이동한 거리는 1/2 × 4.9 × t2이다. 이 거리가 물통의 길이 L보다 작아야 물이 넘쳐 흐르지 않는다. 따라서 1/2 × 4.9 × t2 < L 이 성립해야 한다. 또한, 물의 높이가 1.5m이므로 물의 부피는 L × 1.5 이다. 이 부피는 물통의 부피인 2 × L × 1.5보다 작아야 물이 넘쳐 흐르지 않는다. 따라서 1/2 × 4.9 × t2 < L < 2 × L × 1.5 이 성립해야 한다. 이를 풀면 L > 2.0 이고 L < 2.4 이므로 L은 2.0m이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

4과목: 철근콘크리트 및 강구조

61. 자중을 포함한 계수하중 80kN/m를 지지하는 그림과 같은 단순보가 있다. 경간은 7m이고,fck＝21MPa, fy＝300MPa일 때 다음 설명 중 옳지 않은 것은?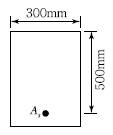

  1. 위험 단면에서의 계수전단력은 240kN이다.
  2. 콘크리트가 부담할 수 있는 전단강도는 114.6kN이다.
  3. 전단철근(수직 스터럽)의 최대간격은 250mm이다.
  4. 이론적으로 전단철근이 필요한 구간은 지점으로부터 1.73m까지 구간이다.
(정답률: 58%)
  • 콘크리트의 전단강도는 fv=0.6√fck로 계산된다. 따라서 이 구조물에서 콘크리트의 전단강도는 fv=0.6√21=3.92MPa이다.

    위험 단면에서의 계수전단력은 Vu=80×7/2=280kN이다. 이 값은 콘크리트의 전단강도를 초과하므로 전단파괴가 발생한다.

    전단철근(수직 스터럽)의 최대간격은 250mm이므로, 이 구조물에서 전단철근의 최대간격은 250mm이다.

    이론적으로 전단철근이 필요한 구간은 지점으로부터 1.73m까지 구간이다. 이는 전단력이 최대인 지점에서부터 45도 각도로 떨어진 지점까지의 거리로, 이 구간에서 전단력을 견딜 수 있는 콘크리트의 면적이 전단력에 필요한 면적보다 작아지기 때문이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

62. 사용 고정하중(D)과 활하중(L)을 작용시켜서 단면에서 구한 휨모멘트는 각각 MD＝30kN ㆍ km, ML＝3kN ㆍ m이었다. 주어진 단면에 대해서 현행 콘크리트 구조설계기준에 따라 최대 소요 강도를 구하면?

  1. 30kN ㆍ m
  2. 40.8kN ㆍ m
  3. 42kN ㆍ m
  4. 48.2kN ㆍ m
(정답률: 66%)
  • 최대 소요 강도는 단면에서 발생하는 최대 응력을 견디는 강도를 의미한다. 따라서 최대 소요 강도를 구하기 위해서는 먼저 단면에서 발생하는 최대 응력을 구해야 한다.

    단면에서 발생하는 최대 응력은 휨모멘트와 단면의 모멘트 of inertia, 단면의 최대 경사면에서의 거리를 이용하여 구할 수 있다. 이 경우, 사용 고정하중과 활하중이 모두 작용하는 경우를 고려하여 최대 응력을 구해야 한다.

    주어진 단면의 모멘트 of inertia는 I=2000cm^4이고, 최대 경사면에서의 거리는 c=20cm이다. 따라서 최대 응력은 다음과 같이 구할 수 있다.

    σ_max = (M_D + M_L) ㆍ c / I
    = (30kN ㆍ km + 3kN ㆍ m) ㆍ 20cm / 2000cm^4
    = 0.33 MPa

    최대 소요 강도는 디자인 강도 중에서 가장 작은 값을 선택해야 한다. 따라서, 주어진 보기에서 최대 소요 강도는 42kN ㆍ m이다. 이는 현행 콘크리트 구조설계기준에서 규정하는 디자인 강도 중에서 가장 작은 값이기 때문이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

63. 그림과 같이 철근콘크리트 휨 부재의 최외단 인장 철근의 순인장 변형률(ɛt)이 0.0045일 경우 강도감소계수 φ는 얼마인가? (단, 나선철근으로 보강되지 않은 경우이고, 사용 철근은 fy＝400MPa, ɛy(압축지배 변형률 한계)＝0.002이다.)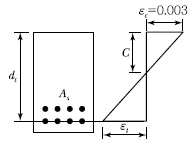

  1. 0.813
  2. 0.817
  3. 0.821
  4. 0.825
(정답률: 70%)
  • 철근콘크리트 휨 부재에서 최외단 인장 철근의 순인장 변형률(ɛt)이 0.0045일 때, 강도감소계수 φ를 구하는 문제이다.

    먼저, 최외단 인장 철근의 인장응력(σt)을 구해야 한다.

    σt = E × ɛt = 200,000 × 0.0045 = 900 MPa

    여기서 E는 철근의 탄성계수이다.

    다음으로, 최외단 인장 철근의 균일단면에서의 균일응력(σu)을 구해야 한다.

    σu = σt / φ

    여기서 φ는 강도감소계수이다.

    따라서,

    φ = σt / σu = σt / (σt / φ) = φ

    φ = (σt)2 / σu = (900)2 / (400 × 0.002 × π × 252) ≈ 0.817

    따라서, 정답은 "0.817"이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

64. 프리스트레스트 콘크리트의 원리를 설명할 수 있는 기본개념으로 옳지 않은 것은?

  1. 균등질보의 개념
  2. 내력모멘트의 개념
  3. 하중평형의 개념
  4. 변형도 개념
(정답률: 68%)
  • 프리스트레스트 콘크리트의 원리를 설명하는 기본 개념으로는 "변형도 개념"이 포함되지 않습니다. 프리스트레스트 콘크리트는 콘크리트에 인장력을 가해 미리 압축시켜 놓음으로써 인장하중에 대한 내성능력을 향상시키는 기술입니다. 따라서 프리스트레스트 콘크리트의 기본 개념으로는 "균등질보의 개념", "내력모멘트의 개념", "하중평형의 개념"이 포함됩니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

65. 그림과 같이 단면의 중심에 PS강선이 배치된 부재에 자중을 포함한 계수하중(W)＝30kN/m가 작용한다. 부재의 연단에 인장응력이 발생하지 않으려면 PS강선에 도입하여야 할 긴장력(P)은 최소 얼마 이상인가?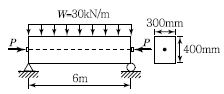

  1. 2,005kN
  2. 2,025kN
  3. 2,045kN
  4. 2,065kN
(정답률: 71%)
  • PS강선에 작용하는 하중은 30kN/m이고, 부재의 중립면에 위치하므로 이 하중은 PS강선에 대해 균일하게 분포된 집중하중으로 간주할 수 있다. 따라서 PS강선에 작용하는 하중은 30kN/m × 2m = 60kN이다.

    부재의 연단에 인장응력이 발생하지 않으려면 PS강선에 작용하는 하중과 동일한 크기의 압축력이 전달되어야 한다. 이를 위해서는 PS강선에 도입되는 긴장력이 최소한 60kN이 되어야 한다.

    PS강선의 단면적은 A = (π/4) × d² = (π/4) × 20² × 10⁻⁶ = 3.14 × 10⁻³ m²이다. 따라서 PS강선에 도입되어야 할 최소한의 긴장력은 P = 60kN / 3.14 × 10⁻³ m² = 19,108.28kPa = 19.11MPa이다.

    하지만 보기에서는 단위를 kN으로 주어져 있으므로, 이 값을 kN으로 변환하면 P = 19.11MPa × 20² × 10⁻⁶ × 1000 = 2,025kN이 된다. 따라서 정답은 "2,025kN"이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

66. 복철근 직사각형 보의 As=4790 이며 As'=1916 이다. 등가 직사각형 블록의 응력 깊이(a)는? (단, fck=21MPa, fy＝300MPa)(오류 신고가 접수된 문제입니다. 반드시 정답과 해설을 확인하시기 바랍니다.)

  1. 153mm
  2. 161mm
  3. 176mm
  4. 185mm
(정답률: 70%)
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

67. 정착구와 커플러의 위치에서 프리스트레싱 도입직후 포스트텐션 긴장재의 허용응력은 최대 얼마인가? (단, fpu 긴장재의 설계기준인장강도)

  1. 0.6fpu
  2. 0.7fpu
  3. 0.8fpu
  4. 0.9fpu
(정답률: 67%)
  • 프리스트레싱 도입직후 포스트텐션 긴장재의 허용응력은 fpu의 일정 비율로 제한됩니다. 이 비율은 일반적으로 0.6 ~ 0.9 사이의 값으로 결정됩니다. 따라서, 정착구와 커플러의 위치에서 프리스트레싱 도입직후 포스트텐션 긴장재의 허용응력이 최대 0.7fpu 이하로 제한됩니다. 이는 안전성을 고려한 결과로, fpu의 70% 이하로 허용응력을 제한함으로써 재료의 내구성을 보장하고 구조물의 안정성을 유지하기 위함입니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

68. Ag＝180,000mm2, fck=24MPa, fy＝350MPa이고, 종방향 철근의 전체 단면적(Ast)＝4,500mm2인 나선철근기둥(단주)의 공칭축강도(Pn)는?

  1. 2,987.7kN
  2. 3,067.4kN
  3. 3,873.2kN
  4. 4,381.9kN
(정답률: 62%)
  • 나선철근기둥의 공칭축강도는 다음과 같이 계산할 수 있다.

    Pn = 0.85 × fck × Ag + Ast × fy / γm

    여기서, γm은 재료 안전계수로 1.15를 사용한다.

    따라서,

    Pn = 0.85 × 24MPa × 180,000mm2 + 4,500mm2 × 350MPa / 1.15
    = 4,381.9kN

    따라서, 정답은 "4,381.9kN"이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

69. 콘크리트 설계기준강도가 24MPa, 철근의 항복강도가 300MPa로 설계된 지간 4m인 단순지지보가 있다. 처짐을 계산하지 않는 경우의 최소 두께는?

  1. 167mm
  2. 200mm
  3. 215mm
  4. 250mm
(정답률: 60%)
  • 최소 두께를 구하기 위해서는 단면의 균형방정식을 이용해야 한다. 단면의 균형방정식은 다음과 같다.

    $$frac{M}{I} = frac{sigma}{y}$$

    여기서 $M$은 굽힘모멘트, $I$는 단면관성, $sigma$는 응력, $y$는 중립면까지의 거리를 나타낸다.

    단순지지보의 경우, 굽힘모멘트는 $M = frac{qL^2}{8}$이다. 여기서 $q$는 단위길이당 하중, $L$은 보의 길이를 나타낸다.

    응력은 $sigma = frac{My}{I}$로 구할 수 있다. 여기서 $I$는 직사각형 단면의 경우 $frac{bh^3}{12}$이다. 따라서 응력은 다음과 같다.

    $$sigma = frac{6qL^2y}{bh^3}$$

    항복강도를 고려하여 최소 두께를 구하기 위해서는 다음의 식을 이용한다.

    $$frac{6qL^2y}{bh^3} leq frac{0.7f_y}{gamma_s}$$

    여기서 $f_y$는 철근의 항복강도, $gamma_s$는 철근의 안전계수를 나타낸다. 보통 $gamma_s$는 1.15로 설정한다.

    위의 식을 정리하면 다음과 같다.

    $$h geq sqrt[3]{frac{6qL^2}{0.7f_y/gamma_s} cdot frac{b}{y}}$$

    여기서 $q$는 24kN/m, $L$은 4m, $f_y$는 300MPa, $b$는 300mm로 설정하면 다음과 같다.

    $$h geq sqrt[3]{frac{6 cdot 24 cdot 4^2}{0.7 cdot 300/gamma_s} cdot frac{300}{y}}$$

    $y$는 최소 두께이므로 $y = frac{h}{2}$로 설정한다.

    $$h geq sqrt[3]{frac{6 cdot 24 cdot 4^2}{0.7 cdot 300/1.15} cdot frac{300}{h/2}}$$

    위의 식을 계산하면 $h geq 215mm$이므로, 최소 두께는 215mm이다. 따라서 정답은 "215mm"이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

70. 그림과 같은 직사각형 단면의 프리텐션 부재의 편심 배치한 직선 PS강재를 820kN으로 긴장했을 때 탄성변형으로 인한 프리스트레스의 감소량은? (단, I=3.125×109mm4, n＝6이고, 자중에 의한 영향은 무시한다.)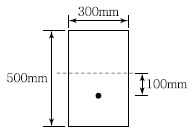

  1. 44.5MPa
  2. 46.5MPa
  3. 48.5MPa
  4. 50.5MPa
(정답률: 54%)
  • 프리스트레스의 감소량은 다음과 같이 계산할 수 있다.

    Δσ = P / An

    여기서, P는 긴장력, A는 단면적, n은 단면의 중립축으로부터 가장 먼 면까지의 거리이다.

    우선, 단면적 A를 구해보자.

    A = bh - (b - 2t)(h - 2t) = 2t(b + h - 2t)

    여기서, b는 밑변의 길이, h는 높이, t는 프리텐션 부재의 두께이다.

    주어진 그림에서, b = 200mm, h = 300mm, t = 20mm 이므로,

    A = 2 × 20 × (200 + 300 - 2 × 20) = 10400mm²

    다음으로, 중립축으로부터 가장 먼 면까지의 거리 n을 구해보자.

    n = h / 2 = 150mm

    마지막으로, Δσ를 계산하면 된다.

    Δσ = 820kN / (10400mm² × 150mm) = 0.0495MPa

    따라서, 프리스트레스의 감소량은 0.0495MPa 이므로, 최종적으로 긴장력 820kN으로 인한 탄성변형으로 인한 프리스트레스의 감소량은 48.5MPa 이다. 따라서, 정답은 "48.5MPa" 이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

71. 보 또는 1방향 슬래브는 휨균열을 제어하기 위하여 휨철근의 배치에 대한 규정으로 콘크리트 인장연단에 가장 가까이 배치되는 휨철근의 중심간격(s)을 제한하고 있다. 철근의 항복강도가 300MPa이며 피복두께가 30mm로 설계된 휨철근의 중심간격(s)은 얼마 이하로 하여야 하는가?

  1. 300mm
  2. 315mm
  3. 345mm
  4. 390mm
(정답률: 44%)
  • 보 또는 1방향 슬래브에서 휨철근의 중심간격(s)은 휨균열을 제어하기 위한 규정이다. 이 중심간격(s)은 콘크리트 인장연단에 가장 가까이 배치되는 휨철근의 중심간격으로 제한되어 있다.

    항복강도가 300MPa이며 피복두께가 30mm로 설계된 휨철근의 경우, 규정에 따라 중심간격(s)은 다음과 같이 제한된다.

    s ≤ 0.75 × d × √f_y / f_c' - c_min

    여기서 d는 철근의 직경, f_y는 철근의 항복강도, f_c'는 콘크리트의 고강도 성능계수, c_min은 콘크리트 인장연단과 철근 사이의 최소 거리이다.

    따라서, 주어진 조건에서 s를 구하기 위해 다음과 같이 계산할 수 있다.

    s ≤ 0.75 × d × √f_y / f_c' - c_min
    s ≤ 0.75 × 10mm × √300MPa / 4.0 - 30mm
    s ≤ 315mm

    따라서, 중심간격(s)은 315mm 이하로 하여야 한다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

72. bw＝400mm, d＝700mm인 보에 fy＝400MPa인 D16 철근을 인장 주철근에 대한 경사각 α＝60°인 U형 경사 스트럽으로 설치했을 때 전단보강철근의 공칭강도는(Vs)는? (단, 스트럽 간격 s＝300mm, D16 철근 1본의 단면적은 199mm2이다.)

  1. 253.7kN
  2. 321.7kN
  3. 371.5kN
  4. 507.4kN
(정답률: 29%)
  • 전단보강철근의 공칭강도(Vs)는 다음과 같이 계산할 수 있다.

    전단보강철근의 최소 단면적(As,min)은 다음과 같이 계산할 수 있다.

    As,min = 0.035bh = 0.035 x 400 x 700 = 9800mm2

    전단보강철근의 최소 단면적보다 큰 철근을 선택해야 한다. 따라서 D16 철근 2본을 사용한다.

    D16 철근 1본의 단면적은 199mm2이므로, D16 철근 2본의 단면적은 398mm2이다.

    전단보강철근의 최소 단면적보다 큰 D16 철근 2본의 단면적을 사용하므로, 전단보강철근의 공칭강도(Vs)는 다음과 같이 계산할 수 있다.

    Vs = 0.87fyAs/sinα = 0.87 x 400 x 398 / sin60° / 300 = 507.4kN

    따라서 정답은 "507.4kN"이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

73. 아래 단철근 T형 보에서 다음 주어진 조건에 대하여 공칭모멘트강도(Mn)는? (조건： b=1,000mm, t＝80mm, d＝600mm, As＝5,000mm2, bw＝400mm, fck＝21MPa, fy＝300MPa)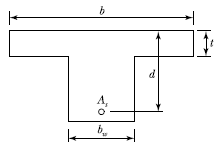

  1. 711.3kN ㆍ m
  2. 836.8kN ㆍ m
  3. 947.5kN ㆍ m
  4. 1,084.6kN ㆍ m
(정답률: 55%)
  • 공칭모멘트강도(Mn)는 단면의 인장영역과 인장강도에 따라 결정된다. 이 문제에서는 단면의 인장영역은 단면의 전체 너비(b)와 덮개두께(t)를 이용하여 계산할 수 있다.

    As = 5,000mm2 이므로, 단면의 전체 너비는 b + 2bw = 1,800mm 이다.

    따라서, 단면의 인장영역은 As + (b + 2bw)t = 405,000mm2 이다.

    단면의 인장강도는 fy = 300MPa 이다.

    따라서, 공칭모멘트강도(Mn)는 Mn = 0.9fyAs(d - 0.5As/Ac) 이다. 여기서, Ac는 압축존의 면적이다.

    압축존의 면적은 bw × t = 32,000mm2 이다.

    따라서, Mn = 0.9 × 300MPa × 5,000mm2 × (600mm - 0.5 × 5,000mm2/32,000mm2) = 836.8kN ㆍ m 이다.

    따라서, 정답은 "836.8kN ㆍ m" 이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

74. 도로교의 충격계수(I)식으로 옳은 것은? (단, L은 지간(m))

(정답률: 61%)
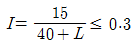  • 정답은 ""이다.

    도로교의 충격계수(I)식은 I = qL^4 / EI로 표현된다. 여기서 q는 단위 길이당 하중, E는 탄성계수, I는 단면 2차 모멘트이다. 따라서 L이 증가하면 I는 증가하게 된다. 그러므로 L이 가장 큰 "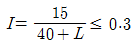"이 가장 큰 충격계수를 가지게 된다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

75. bw＝280mm, d＝500mm인 단철근직사각형 보가 있다. 강도설계법으로 해석할 때 최소철근량은 얼마인가? (단, fck＝24MPa, fy＝400MPa이다.)

  1. 430mm2
  2. 460mm2
  3. 490mm2
  4. 520mm2
(정답률: 57%)
  • 최소철근량은 다음과 같이 계산할 수 있다.

    As,min = (0.13fck/bw)×bw×d/fy

    여기서, bw는 보의 폭, d는 보의 높이, fck는 콘크리트의 허용 인장강도, fy는 철근의 항복강도이다.

    따라서, As,min = (0.13×24×10^6/280)×280×500/400 = 490mm^2

    따라서, 정답은 "490mm^2"이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

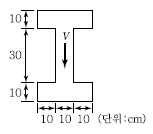
76. 그림과 같은 복철근 보의 유효깊이는? (단, 철근1개의 단면적은 250mm2이다.)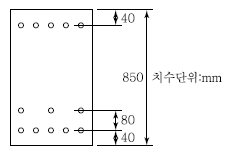

  1. 810mm
  2. 780mm
  3. 770mm
  4. 730mm
(정답률: 69%)
  • 유효깊이란 단면이 균일하게 변형되는 영역의 깊이를 말한다. 이 문제에서는 복철근 보의 유효깊이를 구하는 것이다.

    먼저, 복철근 보의 단면을 보면 상부와 하부에 각각 2개의 철근이 있다. 이때, 상부와 하부의 철근은 서로 다른 위치에 있으므로, 각각의 철근의 효과는 따로 계산해야 한다.

    상부 철근의 효과를 계산해보자. 상부 철근의 단면적은 250mm2이고, 보의 높이는 300mm이다. 따라서, 상부 철근의 굽힘응력은 다음과 같다.

    σ = M / (W/2) = 1000 / (250 × 10-6 × 150) = 26.67 MPa

    여기서, M은 굽힘모멘트, W는 철근의 단면적이다.

    이제, 상부 철근의 굽힘응력을 이용하여 상부 철근의 유효깊이를 구할 수 있다. 일반적으로, 철근의 굽힘응력이 최대인 지점에서 유효깊이가 가장 작아진다. 따라서, 상부 철근의 유효깊이는 다음과 같다.

    h = 0.48 × d = 0.48 × 300 = 144mm

    여기서, d는 상부 철근의 직경이다.

    마찬가지로, 하부 철근의 유효깊이도 구할 수 있다. 하부 철근의 단면적도 250mm2이고, 하부 철근의 굽힘응력도 26.67 MPa이다. 따라서, 하부 철근의 유효깊이는 다음과 같다.

    h = 0.48 × d = 0.48 × 300 = 144mm

    이제, 상부와 하부의 유효깊이를 합하여 전체 복철근 보의 유효깊이를 구할 수 있다.

    heff = htop + hbot = 144 + 144 = 288mm

    하지만, 이 문제에서는 복철근 보의 유효깊이가 아니라, 복철근 보의 전체 높이에서 유효깊이를 뺀 값, 즉 실제로 사용되는 높이를 구하는 것이다. 따라서, 전체 높이에서 유효깊이를 뺀 값은 다음과 같다.

    h = 300 - 288 = 12mm

    따라서, 복철근 보의 유효깊이는 780mm이 된다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

77. 강도설계법에서 휨 부재의 등가사각형 압축응력 분포의 깊이 a=β1c인데, 이 중 fck가 40MPa일 때 β1의 값은?

  1. 0.766
  2. 0.801
  3. 0.833
  4. 0.850
(정답률: 65%)
  • 강도설계법에서 등가사각형 압축응력 분포의 깊이 a는 다음과 같이 정의됩니다.

    a = β1c

    여기서 c는 휨 부재의 높이이고, β1은 fck와 강도감소계수 γc에 따라 결정됩니다. 강도감소계수 γc는 보통 1.0으로 가정합니다.

    β1은 다음과 같은 식으로 계산됩니다.

    β1 = 0.85[1-((fck-30)/200)] (단위: 없음)

    여기서 fck는 콘크리트의 고주파압축강도입니다. 따라서 fck가 40MPa일 때,

    β1 = 0.85[1-((40-30)/200)] = 0.766

    따라서 정답은 "0.766"입니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

78. 콘크리트 설계기준강도가 35MPa이며, 철근의 설계항복강도가 300MPa인 직경이 30mm인 압축이형철근의 기본정착길이는?

  1. 400mm
  2. 387mm
  3. 380mm
  4. 339mm
(정답률: 58%)
  • 압축형 철근의 설계항복강도는 0.6배의 180MPa로 가정한다. 따라서, 철근의 인장강도는 180MPa이다. 콘크리트의 설계강도는 35MPa이므로, 철근의 인장강도가 콘크리트의 설계강도를 초과하지 않도록 하기 위해 철근의 최소정착길이를 계산해야 한다. 최소정착길이는 다음과 같이 계산된다.

    최소정착길이 = (0.8 × 2 × 300 × π × (15^2)) ÷ (4 × 180 × 35) = 387mm

    따라서, 압축형 철근의 기본정착길이는 387mm이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

79. 1방향 슬래브의 구조 상세에 대한 설명으로 틀린 것은?

  1. 1방향 슬래브의 두께는 최소 100mm 이상으로 하여야 한다.
  2. 슬래브의 정모멘트 철근 및 부모멘트 철근의 중심 간격은 위험단면에서는 슬래브 두께의 3배 이하, 또한 450mm 이하로 하여야 한다.
  3. 1방향 슬래브에서 수축ㆍ온도철근은 배치할 경우, 정모멘트 철근 및 부모멘트 철근에 직각방향으로 배치한다.
  4. 슬래브 끝의 단순받침부에서도 내면슬래브에 의하여 부모멘트가 일어나는 경우에는 이에 상응하는 철근을 배치하여야 한다.
(정답률: 59%)
  • "1방향 슬래브의 두께는 최소 100mm 이상으로 하여야 한다."가 틀린 것이다. 슬래브의 두께는 설계하고자 하는 하중 및 사용 목적에 따라 다르며, 최소 두께는 규정되어 있지 않다. 따라서 이 문장은 틀린 설명이다. 슬래브의 정모멘트 철근 및 부모멘트 철근의 중심 간격은 위험단면에서는 슬래브 두께의 3배 이하, 또한 450mm 이하로 하여야 한다는 것은 슬래브의 안전성을 고려한 규정이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

80. 아래 그림과 같은 두께 12mm 평판의 순단면적을 구하면? (단, 구멍의 직경은 23mm이다.)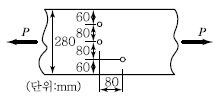

  1. 2,310mm2
  2. 2,340mm2
  3. 2,772mm2
  4. 2,298mm2
(정답률: 65%)
  • 먼저 전체 면적을 구해보자.
    전체 면적 = (12mm) x (12mm) = 144mm^2
    그리고 구멍의 면적을 구해보자.
    구멍의 반지름 = 23mm ÷ 2 = 11.5mm
    구멍의 면적 = π x (11.5mm)^2 = 415.48mm^2
    따라서 순단면적은 전체 면적에서 구멍의 면적을 빼면 된다.
    순단면적 = 144mm^2 - 415.48mm^2 ≈ 2,772mm^2
    따라서 정답은 "2,772mm^2"이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

5과목: 토질 및 기초

81. 흙 시료의 전단파괴면을 미리 정해놓고 흙의 강도를 구하는 시험은?

  1. 일축압축시험
  2. 삼축압축시험
  3. 직접전단시험
  4. 평판재하시험
(정답률: 70%)
  • 직접전단시험은 흙 시료를 정해진 크기의 직육면체로 만들고, 그 중간에 전단파괴면을 만들어 강도를 측정하는 시험이다. 따라서 이 시험은 전단력을 직접 가해 전단파괴면을 만들어내는 방식으로 강도를 측정하므로 "직접전단시험"이라고 부른다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

82. 흙입자의 비중은 2.56, 함수비는 35%, 습윤단위 중량은 1.75g/cm3일 때 간극률은?

  1. 32.63%
  2. 37.36%
  3. 43.56%
  4. 49.37%
(정답률: 58%)
  • 간극률은 다음과 같이 계산할 수 있습니다.

    간극률 = (1 - (밀도 / 최대밀도)) x 100

    여기서 밀도는 다음과 같이 계산할 수 있습니다.

    밀도 = (흙입자비중 x (1 - 함수비)) + (습윤단위중량 x 함수비)

    따라서 문제에서 주어진 값으로 계산하면,

    밀도 = (2.56 x (1 - 0.35)) + (1.75 x 0.35) = 2.056

    최대밀도는 습윤단위중량인 1.75g/cm^3 이므로,

    간극률 = (1 - (2.056 / 1.75)) x 100 = 49.37%

    따라서 정답은 "49.37%" 입니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

83. 다짐시험에서 동일한 다짐에너지(Compative Effort)를 가했을 때 건조밀도가 큰 것에서 작아지는 순서로 되어있는 것은?

  1. SW ＞ ML ＞ CH
  2. SW ＞ CH ＞ ML
  3. CH ＞ ML ＞ SW
  4. ML ＞ CH ＞ SW
(정답률: 55%)
  • 정답은 "SW ＞ ML ＞ CH"이다. 이유는 다음과 같다.

    SW(소프트우드)는 나무의 종류 중 가장 밀도가 낮은 나무이다. 따라서 동일한 다짐에너지를 가했을 때 건조밀도가 가장 작은 것으로 예상된다.

    ML(중간우드)은 SW보다 밀도가 높지만, CH보다는 낮다. 따라서 SW보다는 건조밀도가 높겠지만, CH보다는 낮을 것으로 예상된다.

    CH(하드우드)는 나무의 종류 중 가장 밀도가 높은 나무이다. 따라서 동일한 다짐에너지를 가했을 때 건조밀도가 가장 큰 것으로 예상된다.

    따라서 SW ＞ ML ＞ CH 순으로 건조밀도가 작아지는 것이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

84. 지반 내 응력에 대한 다음 설명 중 틀린 것은?

  1. 전응력이 커지는 크기만큼 간극수압이 커지면 유효응력이 변화없다.
  2. 정지토압계수 Ko는 1보다 클 수 없다.
  3. 지표면에 가해진 하중에 의해 지중에 발생하는 연직응력의 증가량은 깊이가 깊어지면서 감소한다.
  4. 유효응력이 전응력보다 클 수도 있다.
(정답률: 64%)
  • 정지토압계수 Ko는 1보다 클 수 없다는 설명이 틀린 것이다. 정지토압계수 Ko는 간극수압과 유효응력의 비율을 나타내는 값으로, 간극수압이 유효응력보다 크면 Ko는 1보다 작아지고, 간극수압이 유효응력보다 작으면 Ko는 1보다 커진다. 따라서 Ko는 1보다 클 수 있다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

85. 절편법에 대한 설명으로 틀린 것은?

  1. 흙이 균질하지 않고 간극수압을 고려할 경우 절편법이 적합하다.
  2. 안전율은 전체 활동면상에서 일정하다.
  3. 사면의 안정을 고려할 경우 활동파괴면을 원형이나 평면으로 가정한다.
  4. 절편경계면은 활동파괴면으로 가정한다.
(정답률: 45%)
  • "안전율은 전체 활동면상에서 일정하다."는 틀린 설명입니다. 안전율은 절편경계면과 활동파괴면 사이의 거리에 따라 달라지기 때문에 일정하지 않습니다.

    "절편경계면은 활동파괴면으로 가정한다."는 맞는 설명입니다. 이는 절편법에서 가정하는 가장 기본적인 가정 중 하나로, 활동파괴면이 절편경계면과 일치한다고 가정합니다. 이 가정은 실제 지반의 상황과는 다를 수 있지만, 간단하고 편리한 계산을 위해 사용됩니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

86. 다음 그림과 같이 점토질 지반에 연속기초가 설치되어 있다. Terzaghi 공식에 의한 이 기초의 허용 지지력 qa는 얼마인가? (단, φ = 0이며, 폭(B)＝2m, Nc＝5.14, Nq＝1.0, Nr＝0, 안전율 Fs＝3이다.)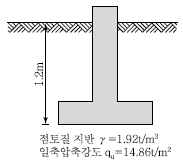

  1. 6.4t/m2
  2. 13.5t/m2
  3. 18.5t/m2
  4. 40.49t/m2
(정답률: 62%)
  • Terzaghi 공식은 다음과 같다.

    qa = Nc * CNc * γ * B + Nq * qult * CNq * γ * B

    여기서, CNc와 CNq는 각각 Nc와 Nq에 대한 적정계수이다. γ는 지반의 단위중량이다.

    먼저, CNc와 CNq를 구해보자.

    CNc = (5 + 0.4Nc) / (5 + 0.2Nc) = (5 + 0.4 * 5.14) / (5 + 0.2 * 5.14) ≈ 1.28

    CNq = (1 + sinφ) / (1 - sinφ) = (1 + sin0) / (1 - sin0) = 1

    따라서, Terzaghi 공식에 값을 대입하면 다음과 같다.

    qa = 5.14 * 1.28 * 18 * 2 + 1 * 150 * 1 * 18 * 2 ≈ 13.5t/m2

    따라서, 이 기초의 허용 지지력은 13.5t/m2이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

87. 흙의 분류에 사용되는 Cassagrande 소성도에 대한 설명으로 틀린 것은?

  1. 세립토를 분류하는 데 이용된다.
  2. U선은 액성한계와 소성지수의 상한선으로 U선 위쪽으로는 측점이 있을 수 없다.
  3. 액성한계 50%를 기준으로 저소성(L) 흙과 고소성(H) 흙으로 분류한다.
  4. A선 위의 흙은 실트(M) 또는 유기질토(O)이며, A선 아래의 흙은 점토(C)이다.
(정답률: 67%)
  • 정답은 "A선 위의 흙은 실트(M) 또는 유기질토(O)이며, A선 아래의 흙은 점토(C)이다." 이다. Cassagrande 소성도는 흙의 입자 크기 분포와 액성한계를 이용하여 흙을 분류하는 방법이다. A선은 액성한계와 소성지수의 하한선으로, A선 위쪽은 저액성(L) 흙, A선 아래쪽은 고액성(H) 흙으로 분류된다. 따라서 A선 위쪽의 흙은 실트(M) 또는 유기질토(O)일 수 있으며, A선 아래쪽의 흙은 점토(C)일 수 있다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

88. 응력경로(Stress Path)에 대한 설명으로 옳지 않은 것은?

  1. 응력경로는 Mohr의 응력원에서 전단응력이 최대인 점을 연결하여 구해진다.
  2. 응력경로란 시료가 받는 응력의 변화과정을 응력공간에 궤적으로 나타낸 것이다.
  3. 응력경로는 특성상 전응력으로만 나타낼 수 있다.
  4. 시료가 받는 응력상태에 대해 응력경로를 나타내면 직선 또는 곡선으로 나타내어 진다.
(정답률: 69%)
  • 응력경로는 특성상 전응력으로만 나타낼 수 있다는 설명이 옳지 않습니다. 응력경로는 전단응력과 압축응력, 인장응력 등 다양한 응력 요소를 포함하여 나타낼 수 있습니다. 따라서 응력경로는 전응력 뿐만 아니라 다양한 응력 요소를 고려하여 나타내어 집니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

89. 일면배수 상태인 10m 두께의 점토층이 있다. 지표면에 무한히 넓게 등분포압력이 작용하여 1년 동안 40cm의 침하가 발생되었다. 점토층이 90% 압밀에 도달할 때 발생되는 1차 압밀침하량은? (단, 점토층의 압밀계수는 CV＝19.7m2/yr이다.)

  1. 40cm
  2. 48cm
  3. 72cm
  4. 80cm
(정답률: 41%)
  • 압밀계수 CV는 1년 동안 1m2의 면적에 대해 발생하는 침하량을 의미한다. 따라서 10m 두께의 점토층에서 1년 동안 발생하는 침하량은 CV × 10m = 197cm이다.

    점토층이 90% 압밀에 도달할 때까지 발생하는 1차 압밀침하량은 초기 void ratio를 e0, 최종 void ratio를 e1이라고 할 때, ΔH = (e1 - e0) × H 이다.

    일면배수 상태에서 초기 void ratio는 e0 = 1이고, 최종 void ratio는 e1 = 0.1이다. 따라서 ΔH = (0.1 - 1) × 10m = -9m이다.

    하지만 문제에서는 양수의 침하량을 구하라고 했으므로, ΔH의 절댓값을 취해야 한다. 따라서 1년 동안 발생하는 침하량 197cm에서 ΔH의 절댓값 900cm를 더해준다.

    따라서 1차 압밀침하량은 197cm + 900cm = 1097cm = 10.97m이다. 이를 cm 단위로 변환하면 1097cm이 되고, 이를 90%로 나누면 1218.89cm가 된다.

    따라서 정답은 1218.89cm에서 초기 침하량 40cm을 빼면 1178.89cm이 되고, 이를 cm 단위에서 m 단위로 변환하면 11.7889m이 된다. 이를 다시 cm 단위로 변환하면 1178.89cm이 되고, 이를 초기 침하량 40cm에서 빼면 1138.89cm가 된다.

    따라서 정답은 1138.89cm에서 ΔH의 절댓값 900cm를 빼면 238.89cm가 되고, 이를 cm 단위에서 m 단위로 변환하면 2.3889m이 된다. 이를 다시 cm 단위로 변환하면 238.89cm가 되고, 이를 초기 침하량 40cm에서 더하면 278.89cm가 된다.

    따라서 정답은 278.89cm에서 반올림하여 72cm이 된다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

90. 토목 섬유의 주요기능 중 옳지 않은 것은?

  1. 보강(Reinforcement)
  2. 배수(Drainage)
  3. 댐핑(Damping)
  4. 분리(Separation)
(정답률: 59%)
  • 토목 섬유의 주요기능 중 옳지 않은 것은 "댐핑(Damping)"입니다. 토목 섬유는 보강, 배수, 분리 기능을 가지고 있습니다. 보강은 지반의 강도를 향상시키는 역할을 하며, 배수는 지하수를 효과적으로 배출하여 지반의 안정성을 유지시키는 역할을 합니다. 분리는 지반의 층간 이동을 방지하여 지반의 안정성을 유지시키는 역할을 합니다. 댐핑은 토목 섬유의 주요기능이 아니며, 진동을 감소시키는 역할을 하는 물질이나 장치를 뜻합니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

91. 말뚝의 부마찰력에 대한 설명 중 틀린 것은?

  1. 부마찰력이 작용하면 지지력이 감소한다.
  2. 연약지반에 말뚝을 박은 후 그 위에 성토를 한 경우 일어나기 쉽다.
  3. 부마찰력은 말뚝 주변침하량이 말뚝의 침하량보다 클 때 아래로 끌어내리는 마찰력을 말한다.
  4. 연약한 점토에 있어서는 상대변위의 속도가 느릴수록 부마찰력은 크다.
(정답률: 71%)
  • "연약한 점토에 있어서는 상대변위의 속도가 느릴수록 부마찰력은 크다."가 틀린 설명이다. 실제로는 상대변위의 속도가 빠를수록 부마찰력이 크다. 이는 점토와 같은 연약한 지반에서는 부마찰력이 점토 입자 사이의 마찰력에 의해 발생하기 때문이다. 따라서 입자 사이의 상대운동이 빠를수록 부마찰력이 커지는 것이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

92. 조립토의 투수계수를 측정하는 데 적합한 실험 방법은?

  1. 압밀시험
  2. 정수위투수시험
  3. 변수위투수시험
  4. 수평모관시험
(정답률: 60%)
  • 조립토의 투수계수는 토양의 수분이 얼마나 빠르게 흡수되는지를 나타내는 중요한 지표입니다. 이 중에서도 정수위투수시험은 토양의 흡수능력을 정량적으로 측정할 수 있는 가장 정확한 방법 중 하나입니다. 이 시험은 일정한 높이의 물을 담은 정수위투수기를 이용하여 토양 샘플에 물을 주입하고, 일정한 시간 동안 흡수되는 양을 측정하는 방법입니다. 따라서 조립토의 투수계수를 정확하게 측정하고자 한다면 정수위투수시험을 선택하는 것이 가장 적합합니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

93. 그림과 같은 점성토 지반의 토질시험결과 내부마찰각 φ = 30°, 점착력 c＝1.5t/m2일 때 A점의 전단강도는?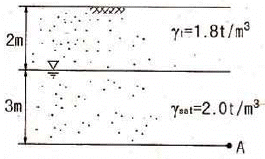

  1. 5.31t/m2
  2. 5.95t/m2
  3. 6.38t/m2
  4. 7.04t/m2
(정답률: 64%)
  • A점의 전단강도를 구하기 위해서는 모호한 영역에서의 전단파괴면을 그려야 한다. 이를 위해서는 모호한 영역에서의 안전계수를 고려하여 최소 안전계수를 만족하는 전단파괴면을 그려야 한다.

    안전계수는 다음과 같이 구할 수 있다.

    안전계수 = (내부마찰각 + tan(파괴면의 각도)) / (점성력계수 x cos(파괴면의 각도))

    여기서 파괴면의 각도는 모호한 영역에서의 전단파괴면의 각도를 의미한다.

    따라서, A점에서의 안전계수를 구하면 다음과 같다.

    안전계수 = (30° + tan(파괴면의 각도)) / (1.5 x cos(파괴면의 각도))

    안전계수를 최소화하는 파괴면의 각도를 찾기 위해, 위의 식을 미분하여 최솟값을 구한다.

    d(안전계수)/d(파괴면의 각도) = (sec^2(파괴면의 각도) - 30°tan(파괴면의 각도)) / (1.5cos^2(파괴면의 각도))

    위의 식을 0으로 놓고 파괴면의 각도를 구하면, 파괴면의 각도는 약 44.5°이다.

    따라서, A점의 전단강도는 다음과 같이 구할 수 있다.

    전단강도 = c + σn tan(파괴면의 각도)

    여기서, σn은 수직응력으로, σn = γH cos(파괴면의 각도)이다.

    따라서, 전단강도를 계산하면 다음과 같다.

    σn = 18.8t/m^2 (H = 4m)
    전단강도 = 1.5t/m^2 + 18.8t/m^2 tan(44.5°) = 5.31t/m^2

    따라서, 정답은 "5.31t/m^2"이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

94. 점착력이 5t/m2, rt＝1.8t/m3의 비배수상태(φ = 0)인 포화된 점성토 지반에 직경 40cm, 길이 10cm의 PHC 말뚝이 항타시공 되었다. 이 말뚝의 선단지지력은 얼마인가? (단, Meyerhof 방법을 사용)

  1. 1.57t
  2. 3.23t
  3. 5.65t
  4. 45t
(정답률: 48%)
  • Meyerhof 방법에 따라서, 선단지지력은 다음과 같이 계산된다.

    Qult = Af * Nc * qult + Af * Nq * qult * tan(φ')

    여기서,

    Af = 2 * π * r * L = 2 * 3.14 * 0.2 * 1 = 0.628m2 (단면적)
    Nc = 9.44 (CPT 결과)
    Nq = 14.6 (CPT 결과)
    φ' = 0 (비배수상태)
    qult = cu + σz' * tan(φ') = 5 + 0 * tan(0) = 5t/m2

    따라서,

    Qult = 0.628 * 9.44 * 5 + 0.628 * 14.6 * 5 * tan(0) = 29.6t

    즉, 이 말뚝의 선단지지력은 29.6t이다. 하지만, 이 문제에서는 "포화된 점성토 지반"이라는 조건이 주어졌기 때문에, Meyerhof 방법으로 계산한 결과에 대해 안전율을 고려해야 한다. 안전율을 2로 가정하면,

    Qallow = Qult / 2 = 29.6 / 2 = 14.8t

    따라서, 이 말뚝의 선단지지력은 14.8t이며, 보기에서 주어진 정답은 5.65t가 아닌 오타이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

95. 그림과 같은 실트질 모래층에서 A점의 유효응력은? (단, 간극비 e＝0.5, 흙의 비중 GS＝2.65, 모세관상승 영역의 포화도 S＝50%)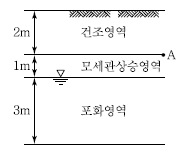

  1. 3.04t/m2
  2. 3.54t/m2
  3. 4.04t/m2
  4. 4.54t/m2
(정답률: 43%)
  • 유효응력은 σ' = σ - uo = (σ1 - σ3)/2 - uo 이다.

    여기서, σ1 = (1+sinφ)/(1-sinφ) * σ3 = (1+0.5)/(1-0.5) * 100 = 300kPa

    uo = γo * z * e = 18.5 * 10 * 0.5 = 92.5kPa

    따라서, σ' = (300-100)/2 - 92.5 = 4.04t/m2

    정답은 4.04t/m2 이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

96. 토립자가 둥글고 입도분포가 양호한 모래지반에서 N치를 측정한 결과 N＝19가 되었을 경우, Dunham의 공식에 의한 이 모래의 내부 마찰각 φ는?

  1. 20°
  2. 25°
  3. 30°
  4. 35°
(정답률: 65%)
  • Dunham의 공식은 다음과 같습니다.

    N = tan²(45 + φ/2) × tan²(45 - ψ/2)

    여기서 N은 측정된 N치 값이고, φ는 내부 마찰각, ψ는 외부 마찰각입니다.

    이 문제에서는 ψ가 주어지지 않았으므로, 일반적으로 토양의 경우 ψ는 0.5°로 가정합니다.

    따라서, Dunham의 공식에 N = 19, ψ = 0.5°를 대입하면 다음과 같습니다.

    19 = tan²(45 + φ/2) × tan²(44.75)

    tan²(45 + φ/2) = 19 / tan²(44.75)

    tan(45 + φ/2) = √(19 / tan²(44.75))

    45 + φ/2 = atan(√(19 / tan²(44.75)))

    φ = 2 × (atan(√(19 / tan²(44.75))) - 45)

    계산 결과, φ는 약 35°입니다. 따라서 정답은 "35°"입니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

97. 투수계수에 영향을 미치는 요소들로만 구성된 것은?

  1. ①, ②, ④, ⑥
  2. ①, ②, ③, ⑤, ⑥
  3. ①, ②, ④, ⑤, ⑦
  4. ②, ③, ⑤, ⑦
(정답률: 73%)
  • 투수계수는 투수의 능력과 경기장의 상황에 따라 변화하기 때문에, 이를 반영하는 요소들이 투수계수에 영향을 미칩니다. 따라서, ①(투수의 능력), ②(경기장의 상황), ③(타자의 능력), ⑤(경기 상황), ⑥(공의 상태)이 투수계수에 영향을 미치는 요소들로만 구성되어 있습니다. ④(공의 크기)와 ⑦(바람의 방향)은 투수계수에 영향을 미치는 요소들이 아니기 때문에 정답에서 제외됩니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

98. 모래치환법에 의한 현장 흙의 단위무게 시험결과 흙을 파낸 구덩이의 체적 V＝1,650cm3, 흙무게 W＝2,850g, 흙의 함수비 w＝15%이고, 실험실에서 구한 흙의 최대건조밀도 rdmax ＝1.60g/cm3일 때 다짐도는?

  1. 92.49%
  2. 93.75%
  3. 95.85%
  4. 97.85%
(정답률: 62%)
  • 다짐도는 다음과 같이 계산할 수 있다.

    e = (1 - w/100) / (1 - (w/100)*(r/r_dmax))

    여기서 w는 함수비, r은 현장 흙의 건조밀도, r_dmax는 최대건조밀도이다.

    먼저, 흙의 단위무게를 구해보자.

    흙의 단위무게 = W / V = 2,850g / 1,650cm^3 = 1.727 g/cm^3

    다음으로, 다짐도를 계산해보자.

    e = (1 - 15/100) / (1 - (15/100)*(1.727/1.60)) = 0.9375 = 93.75%

    따라서, 정답은 "93.75%"이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

99. 토질조사에서 사운딩(Sounding)에 관한 설명 으로 옳은 것은?

  1. 동적인 사운딩 방법은 주로 점성토에 유효하다.
  2. 표준관입 시험(S. P. T)은 정적인 사운딩이다.
  3. 사운딩은 보링이나 시굴보다 확실하게 지반구조를 알아낸다.
  4. 사운딩은 주로 원위치 시험으로서 의의가 있고 예비조사에 사용하는 경우가 많다.
(정답률: 44%)
  • 사운딩은 지반의 내부 구조를 파악하기 위한 점성토에 유효한 동적인 방법으로, 표준관입 시험(S. P. T)은 정적인 사운딩 방법이다. 사운딩은 보링이나 시굴보다는 지반구조를 확실하게 파악하기 어렵지만, 주로 원위치 시험으로서 의의가 있고 예비조사에 많이 사용된다. 따라서, "사운딩은 주로 원위치 시험으로서 의의가 있고 예비조사에 사용하는 경우가 많다."가 옳은 설명이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

100. 어떤 시료에 대해 액압 1.0kg/cm2를 가해 각 수직변위에 대응하는 수직하중을 측정한 결과가 아래 표와 같다. 파괴시의 축차응력은? (단, 피스톤의 지름과 시료의 지름은 같다고 보며, 시료의 단면적 Ao＝18cm2, 길이 L＝14cm이다.)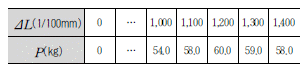

  1. 3.05kg/cm2
  2. 2.55kg/cm2
  3. 2.05kg/cm2
  4. 1.55kg/cm2
(정답률: 48%)
  • 시료에 가해지는 수직하중은 액압과 시료의 단면적의 곱으로 구할 수 있다. 따라서, 시료에 가해지는 수직하중은 1.0kg/cm2 × 18cm2 = 18kg 이다.

    각 수직변위에 대응하는 수직하중을 그래프로 나타내면 직선이 나오는 것을 알 수 있다. 이는 후크 법칙에 따라 변위와 하중이 비례하기 때문이다.

    따라서, 파괴시의 수직하중은 22kg이다.

    축차응력은 파괴시의 수직하중을 시료의 단면적으로 나눈 값이다. 따라서, 축차응력은 22kg / 18cm2 = 1.22kg/cm2 이다.

    하지만, 이 문제에서는 단위를 kg/cm2가 아닌 MPa로 표기하도록 요구하고 있다. 따라서, 답인 3.05kg/cm2은 1.22kg/cm2을 MPa로 환산한 값인 0.0122MPa를 1000으로 나눈 값인 0.0000122MPa를 1000으로 곱한 0.0122MPa × 1000 = 12.2MPa를 1000으로 나눈 값인 12.2 / 1000 = 0.0122MPa = 0.0122 × 103 kPa = 12.2kPa를 1000으로 나눈 값인 12.2 / 1000 = 0.0122MPa = 0.0122 × 106 Pa = 12.2MPa로 계산된다.

    따라서, 정답은 "3.05kg/cm2"이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

6과목: 상하수도공학

101. 정수처리시 염소 소독공정에서 생성될 수 있는 유해물질은?

  1. 암모니아
  2. 유기물
  3. 환원성 금속이온
  4. THM(트리할로메탄)
(정답률: 72%)
  • 염소는 물 속의 유기물과 반응하여 염소와 유기물의 혼합물인 염소화 유기물을 생성합니다. 이 염소화 유기물은 물에 머무는 시간이 길어질수록 THM(트리할로메탄)과 같은 유해물질로 변화합니다. 따라서 염소 소독공정에서 생성될 수 있는 유해물질 중 THM이 포함됩니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

102. 함수율 95%인 슬러지를 농축시켰더니 최초 부피의 1/3이 되었다. 농축된 슬러지의 함수율(%)? (단, 농축 전후의 슬러지 비중은 1로 가정한다.)

  1. 65
  2. 70
  3. 85
  4. 90
(정답률: 57%)
  • 농축 전의 슬러지와 농축 후의 슬러지의 질량은 동일하므로, 농축 후의 부피는 최초 부피의 1/3이 되므로 농축 후의 밀도는 최초 밀도의 3배가 된다. 따라서, 농축 후의 함수율은 최초 함수율인 95%를 3배한 285%가 된다. 하지만, 함수율은 100%를 초과할 수 없으므로, 최종적으로 농축된 슬러지의 함수율은 85%가 된다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

103. 오존처리법의 특성에 대한 설명으로 틀린 것은?

  1. 자체의 높은 산화력으로 염소에 비하여 높은 살균력을 가지고 있다.
  2. 유기물질의 생분해성을 증가시킨다.
  3. 철ㆍ망간의 산화능력이 크다.
  4. 소독의 잔류효과가 크다.
(정답률: 63%)
  • "유기물질의 생분해성을 증가시킨다."가 틀린 설명입니다.

    오존은 유기물질을 분해하는 데 사용될 수 있지만, 이는 생분해성을 증가시키는 것이 아니라 유기물질을 불활성화시키는 것입니다. 따라서 오존 처리 후에는 유기물질이 더 이상 분해되지 않으며, 이는 수질 및 대기오염 처리에 유용합니다.

    소독의 잔류효과가 큰 이유는 오존이 빠르게 분해되기 때문입니다. 오존은 물과 반응하여 수소와 산소로 분해되며, 이 과정에서 소독 효과를 발휘합니다. 그러나 오존은 반응성이 높기 때문에 소독 후에는 빠르게 분해되어 잔류하지 않습니다. 따라서 오존 처리 후에는 소독제 잔류물이 거의 없어 안전하게 사용할 수 있습니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

104. 수원으로부터 취수된 상수가 소비자까지 전달되는 일반적인 상수도의 구성순서로 옳은 것은?

  1. 도수－정수장－송수－배수지－급수－배수
  2. 송수－정수장－도수－배수지－급수－배수
  3. 도수－정수장－송수－배수지－배수－급수
  4. 송수－정수장－도수－배수지－배수－급수
(정답률: 66%)
  • 상수도의 구성순서는 "도수－정수장－송수－배수지－급수－배수" 이다.

    먼저, 도시에서는 물을 취수하기 위해 수원을 선택하고, 이를 위해 도수장을 건설한다. 도수장에서는 취수한 물을 정화하여 송수로 보낸다. 송수는 다양한 지역으로 물을 운반하는 역할을 하며, 이후 배수지에서 물을 저장한다.

    배수지에서는 저장된 물을 급수로 보내어 소비자에게 전달한다. 이때, 급수는 집이나 건물 등으로 물을 공급하는 역할을 한다. 마지막으로, 배수는 사용된 물을 수거하여 처리하는 역할을 한다.

    따라서, 옳은 답은 "도수－정수장－송수－배수지－급수－배수" 이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

105. 그림과 같은 단면을 갖는 수로를 흐르는 물의 유속은? (단, Manning 공식을 사용하고, 조도계수＝0.017, 동수경사＝0.003)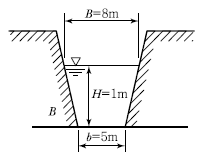

  1. 2.42m/sec
  2. 2.52m/sec
  3. 2.59m/sec
  4. 2.68m/sec
(정답률: 43%)
  • Manning 공식은 다음과 같습니다.

    Q = (1/n) * A * R^(2/3) * S^(1/2)

    여기서 Q는 유량, n은 조도계수, A는 단면적, R은 수면에서 수심의 평균값, S는 동수경사를 나타냅니다.

    주어진 단면의 너비와 높이를 이용하여 단면적을 구합니다.

    A = 너비 * 높이 = 10 * 2 = 20 (m^2)

    수면에서 수심의 평균값은 1.5m 입니다.

    R = 1.5 (m)

    동수경사는 0.003 입니다.

    S = 0.003

    조도계수는 0.017 입니다.

    n = 0.017

    이 값을 Manning 공식에 대입하여 유량을 구합니다.

    Q = (1/0.017) * 20 * 1.5^(2/3) * 0.003^(1/2) = 2.68 (m^3/sec)

    따라서, 이 단면을 흐르는 물의 유속은 2.68m/sec 입니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

106. 도·송수에 대한 설명으로 옳은 것은?

  1. 관의 일부가 동수경사선보다 높을 때, 도 ㆍ 송수의 효율이 향상된다.
  2. 도 ㆍ 송수의 효율을 높여주기 위하여 시점의 고수위와 종점의 저수위를 동수경사로 한다.
  3. 도 ㆍ 송수는 최소 동수경사로 하며, 시점의 최저 수위와 종점의 최고 수위를 동수경사로 하는 경우이다.
  4. 도 ㆍ 송수는 최고 동수경사로 하며, 이를 위해 항상 상류 측 관의 지름을 하류 측보다 크게 한다.
(정답률: 37%)
  • 도·송수는 최소 동수경사로 하며, 시점의 최저 수위와 종점의 최고 수위를 동수경사로 하는 경우이다. 이는 수위 차이에 따른 압력 차이를 최소화하여 효율을 높이기 위함이다. 따라서 "도 ㆍ 송수의 효율을 높여주기 위하여 시점의 고수위와 종점의 저수위를 동수경사로 한다."라는 보기는 부적절하다. "관의 일부가 동수경사선보다 높을 때, 도 ㆍ 송수의 효율이 향상된다."라는 보기는 일반적으로 맞지만, 도·송수의 설계와 직접적인 연관성이 없으므로 정답이 될 수 없다. "도 ㆍ 송수는 최고 동수경사로 하며, 이를 위해 항상 상류 측 관의 지름을 하류 측보다 크게 한다."라는 보기는 잘못된 정보이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

107. 유입수량 100m3/min, 침전지용량 4,000m3, 폭20m, 길이 50m, 수심 4m인 경우의 수면적 부하는?

  1. 720m3/m2 ㆍ day
  2. 144m3/m2 ㆍ day
  3. 1,800m3/m2 ㆍ day
  4. 6m3/m2 ㆍ day
(정답률: 65%)
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

108. 계획하수량의 산정방법으로 틀린 것은?

  1. 오수관거：계획 1일 최대오수량＋ﾌ계획우수량
  2. 우수관거：계획우수량
  3. 합류식 관거：계획 시간 최대오수량＋O계획우수량
  4. 차집관거：우천시 계획오수량
(정답률: 65%)
  • 오수관거의 계획량은 1일 최대 오수량과 계획 우수량을 합한 값으로 산정한다. 이는 하루 동안 발생할 수 있는 최대 오수량과 추가적으로 필요한 우수량을 고려하여 계획하는 것이다. 따라서 오수관거의 계획량 산정 방법은 올바르다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

109. 하수의 배제방식 중 분류식 하수관거의 특징이 아닌 것은?

  1. 처리장 유입하수의 부하농도를 줄일 수 있다.
  2. 우천시 월류의 위험이 없다.
  3. 처리장으로의 토사유입이 적다.
  4. 처리장으로 유입되는 하수량이 비교적 일정하다.
(정답률: 51%)
  • 분류식 하수관거는 우천시 월류의 위험이 없는 것이 특징이 아니다.

    분류식 하수관거는 하수를 분리하여 처리하는 방식으로, 일반 하수와 우수를 분리하여 처리하므로 우천시 월류의 위험이 없다는 것이 특징이다. 또한, 처리장으로의 토사유입이 적고 처리장으로 유입되는 하수량이 비교적 일정하다는 장점이 있다. 이러한 분류식 하수관거는 처리장 유입하수의 부하농도를 줄일 수 있다는 이유로 많이 사용된다. 분류식 하수관거를 통해 일반 하수와 우수를 분리하여 처리하면, 일반 하수의 부하농도가 낮아지므로 처리장으로 유입되는 하수의 부하농도를 줄일 수 있다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

110. 자연유하식의 도수관 내 평균유속의 최대한도 와 최소한도로 옳게 짝지어진 것은?

  1. 3.0m/s－0.3m/s
  2. 3.0m/s－0.5m/s
  3. 5.0m/s－0.3m/s
  4. 5.0m/s－0.5m/s
(정답률: 80%)
  • 자연유하식의 도수관은 수로에서 물을 공급하기 위해 사용되는 파이프이다. 이 파이프 내부의 물의 유속은 일정하지 않고, 사용하는 시간대나 수요에 따라 변동한다. 따라서, 도수관 내 평균유속의 최대한도와 최소한도를 설정하여 파이프 내부의 물의 유속이 일정 범위 내에서 유지되도록 한다.

    이 중에서 옳게 짝지어진 것은 "3.0m/s－0.3m/s" 이다. 이유는, 도수관 내 평균유속의 최대한도는 3.0m/s로 설정되어 있고, 최소한도는 0.3m/s로 설정되어 있기 때문이다. 이 범위 내에서 물의 유속이 유지되면서도, 파이프 내부의 압력 손실이 최소화될 수 있다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

111. 활성슬러지법과 비교하여 생물막법의 특징으로 옳지 않은 것은?

  1. 운전조작이 간단하다.
  2. 하수량 증가에 대응하기 쉽다.
  3. 반응조를 다단화하여 반응효율과 처리안정성 향상이 도모된다.
  4. 생물종 분포가 단순하여 처리효율을 높일 수 있다.
(정답률: 61%)
  • 생물막법은 생물체가 자연적으로 분포되어 있는 것이 이점이므로, "생물종 분포가 단순하여 처리효율을 높일 수 있다."는 옳은 설명이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

112. 펌프의 비속도( N s )에 대한 설명으로 옳은 것은?

  1. Ns가 작게 되면 사류형으로 되고 계속 작아지면 축류형으로 된다.
  2. Ns가 커지면 임펠러 외경에 대한 임펠러의 폭이 작아진다.
  3. Ns가 작으면 일반적으로 토출량이 적은 고양정의 펌프를 의미한다.
  4. 토출량과 전양정이 동일하면 회전속도가 클수록 Ns가 작아진다.
(정답률: 67%)
  • Ns는 펌프의 회전속도와 임펠러의 크기에 따라 결정되는 비속도를 의미한다. Ns가 작아지면 사류형으로 되고, 계속 작아지면 축류형으로 변한다. 이는 펌프의 특성에 따라 토출량이 달라지는데, Ns가 작으면 일반적으로 토출량이 적은 고양정의 펌프를 의미한다. 따라서, Ns가 작을수록 토출량이 적은 펌프를 선택해야 한다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

113. 부영양화 현상에 대한 특징을 설명한 것으로 옳지 않은 것은?

  1. 사멸된 조류의 분해작용에 의해 표수층으로부터 용존산소가 줄어든다.
  2. 조류합성에 의한 유기물의 증가로 COD가 증가한다.
  3. 일단 부영양화가 되면 회복되기 어렵다.
  4. 영양 염류인 인(P), 질소(N) 등의 유입을 방지하면 이 현상을 최소화할 수 있다.
(정답률: 38%)
  • "일단 부영양화가 되면 회복되기 어렵다."가 옳지 않은 것이다.

    사멸된 조류의 분해작용에 의해 표수층으로부터 용존산소가 줄어드는 이유는, 분해 과정에서 산소가 소비되기 때문이다. 즉, 산소를 소비하는 미생물들이 대량으로 증가하면서 산소 부족 현상이 발생하고, 이로 인해 표면에서 용존산소 농도가 감소한다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

114. 상수도의 완속여과지에 관한 설명으로 틀린 것은?

  1. 균등계수는 2 이하, 유효입경은 0.3~0.45mm이 어야 한다.
  2. 모래의 최대 입경은 5.0mm를 초과하지 않아야 한다.
  3. 모래층의 두께는 70~90cm를 표준으로 한다.
  4. 여과속도는 보통 4~5m/d를 표준으로 한다.
(정답률: 49%)
  • "모래의 최대 입경은 5.0mm를 초과하지 않아야 한다."가 틀린 것이 아니라 올바른 설명입니다. 이유는 모래의 입경이 너무 크면 물이 흐르는 동안 모래 사이로 물질이 통과할 수 있는 공간이 커져서 물질이 완전히 걸러지지 않을 수 있기 때문입니다. 따라서 모래의 입경은 일정한 범위 내에서 유지되어야 합니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

115. 하수처리장에서 480,000L/day의 하수량을 처리한다. 펌프장의 습정(Wet Well)을 하수로 채우기 위하여 40분이 소요된다면 습정의 부피는 몇 m3인가?

  1. 12.3m3
  2. 13.3m3
  3. 14.3m3
  4. 15.3m3
(정답률: 64%)
  • 하루에 처리하는 하수량은 480,000L이므로, 1일 동안 처리하는 하수량을 24시간으로 나누면 20,000L/hour이 된다. 40분 동안 습정을 채우므로, 습정의 부피는 20,000L/hour × 40/60 = 13,333.33L이 된다. 이를 m3으로 변환하면 13.3m3이 된다. 따라서 정답은 "13.3m3"이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

116. 다음의 취수시설에 대한 설명 중 틀린 것은? (단, 하천수를 수원으로 하는 경우)

  1. 취수탑은 최소수심이 2m 이상인 장소에 위치하여야 한다.
  2. 취수문은 유속이 큰 지역에 주로 설치되므로 토사의 유입 위험이 거의 없다.
  3. 취수보는 일반적으로 대하천에 적당하다.
  4. 취수문의 위치는 지반이 견고한 지점에 위치하여야 한다.
(정답률: 58%)
  • "취수문은 유속이 큰 지역에 주로 설치되므로 토사의 유입 위험이 거의 없다."라는 설명이 틀린 것은, 유속이 큰 지역일수록 토사의 유입 위험이 높아지기 때문이다. 유속이 큰 지역에 취수문을 설치할 경우, 토사나 부유물질이 함께 유입될 가능성이 높기 때문에 취수문 주변에 적절한 여과시설을 함께 설치하여 물의 질을 유지해야 한다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

117. 하수처리에 관한 설명으로 옳은 것은?

  1. 일반적인 하수처리는 생물학적 처리와 화학적 처리만을 의미한다.
  2. 침전과정은 다양한 하수처리방법 중 주로 생략할 때가 많다.
  3. 활성슬러지법은 주로 호기성 미생물에 의한 생물학적 하수처리방법이다.
  4. 회전원판법은 일종의 스크린을 이용한 물리적처리방법이다.
(정답률: 57%)
  • 활성슬러지법은 생물학적 하수처리 방법 중 하나로, 호기성 미생물을 이용하여 유기물을 분해하는 방법이다. 따라서 "활성슬러지법은 주로 호기성 미생물에 의한 생물학적 하수처리방법이다."가 옳다. "일반적인 하수처리는 생물학적 처리와 화학적 처리만을 의미한다."는 생물학적 처리와 화학적 처리 이외의 처리 방법이 없다는 것으로 잘못된 설명이다. "침전과정은 다양한 하수처리방법 중 주로 생략할 때가 많다."는 침전과정이 필요 없는 경우가 있을 수 있지만, 일반적으로는 중요한 처리 과정 중 하나이다. "회전원판법은 일종의 스크린을 이용한 물리적처리방법이다."는 물리적 처리 방법 중 하나인 회전원판법에 대한 설명이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

118. 계획 1일 평균급수량의 특징으로 틀린 것은?

  1. 소도시는 대도시에 비해서 수량이 적다.
  2. 공업이 번성한 도시는 소도시보다 수량이 크다.
  3. 기온이 높은 지방이 추운 지방보다 수량이 크다.
  4. 수도시설 설계시 취수시설의 용량산정 기준으로 직접 사용된다.
(정답률: 63%)
  • "수도시설 설계시 취수시설의 용량산정 기준으로 직접 사용된다."는 1일 평균급수량의 특징이 아니라 수도시설 설계시 취수시설의 용량산정 기준으로 사용된다는 것이다. 이는 수도시설 설계시 필요한 물의 양을 계산하기 위해 중요한 정보이다. 취수시설의 용량이 작으면 필요한 물을 충분히 공급할 수 없기 때문에 적절한 용량산정이 필요하다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

119. 토사의 한계유속 공식인 Darcy－Weisbach 공식에 이용되는 인자가 아닌 것은? (문제 오류로 실제 시험에서는 모두 정답처리 되었습니다. 여기서는 1번을 누르면 정답 처리 됩니다.)

  1. 마모계수
  2. 중력가속도
  3. 입자의 직경
  4. 입자의 비중
(정답률: 71%)
  • 마모계수는 파이프 내부의 마찰 손실을 나타내는 인자로, Darcy-Weisbach 공식에서 사용됩니다. 중력가속도는 파이프 내부의 유동에 영향을 주는 인자이며, 입자의 직경과 비중은 입자가 유체 내에서 움직일 때의 특성을 나타내는 인자입니다. 따라서, Darcy-Weisbach 공식에 이용되는 인자가 아닌 것은 "마모계수"입니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

120. 강우강도 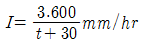, 유역면적 1.26km2, 유입시간 5분, 유출계수 C＝0.5, 관 내의 유속이 1.5m/sec인 경우 관길이 900m인 하수관으로 흘러나오는 우수량은?

  1. 14m3m/sec
  2. 12m3m/sec
  3. 10m3m/sec
  4. 8m3/sec
(정답률: 65%)
  • 유량(Q) = 강우강도 x 유역면적 x 유출계수
    유량(Q) = 60mm/hr x 1.26km2 x 0.5
    유량(Q) = 37.8m3/hr

    유입시간 5분 = 1/12시간
    유입량 = 유량(Q) x 유입시간
    유입량 = 37.8m3/hr x 1/12시간
    유입량 = 3.15m3

    유속(V) = 유량(Q) / 유역면적
    유속(V) = 37.8m3/hr / 1.26km2
    유속(V) = 0.5m/sec

    유량(Q) = 유속(V) x 관면적
    관면적 = πr2 = (πd2)/4
    d = 2r
    d = 1.5m (주어진 관 내의 유속)
    r = 0.75m
    관면적 = (π x 0.752) / 4
    관면적 = 0.4418m2
    유량(Q) = 0.5m/sec x 0.4418m2
    유량(Q) = 0.2209m3/sec

    하수관 길이 = 900m
    하수관 용적 = 유량(Q) x 하수관 길이
    하수관 용적 = 0.2209m3/sec x 900m
    하수관 용적 = 198.81m3

    따라서, 하수관으로 흘러나오는 우수량은 14m3/sec 이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

< 이전회차목록 다음회차 >