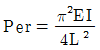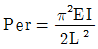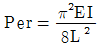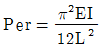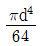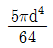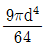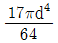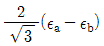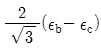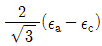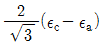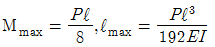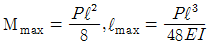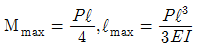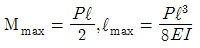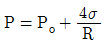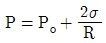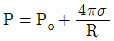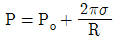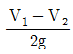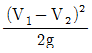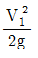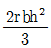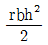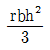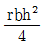일반기계기사 필기 기출문제복원 (2012-09-15)

일반기계기사
(2012-09-15 기출문제)

목록

1과목: 재료역학

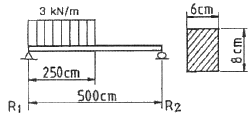
1. 그림과 같은 외팔보에 대한 전단력 선도는?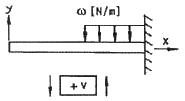

(정답률: 47%)
  • 외팔보의 전단력은 외팔보의 중심에서 가장 크게 작용하는 것으로, 이는 외팔보의 중심에 위치한 "" 지점에서 발생합니다. 따라서 정답은 "" 입니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

2. 다음과 같이 집중하중과 등분포하중을 받는 보의 중앙점 c에서의 처짐의 크기는 약 몇 mm인가? (단, 굽힘강성 EI = 10MN · m2이다.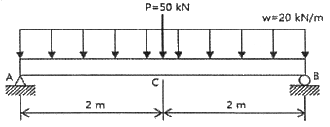

  1. 13.3
  2. 18.6
  3. 23.4
  4. 28.6
(정답률: 54%)
  • 이 보는 균일한 단면과 균일한 재질을 가지고 있으므로, 중앙점 c에서의 처짐은 집중하중과 등분포하중의 합에 의해 결정된다.

    집중하중의 경우, P = 20kN이 중앙점 c에서 작용하므로, 이에 의한 처짐은 다음과 같다.

    δP = PL3/48EI = (20 × 103) × (33) / (48 × 10 × 106) = 0.0025m = 2.5mm

    등분포하중의 경우, w = 10kN/m이 중앙점 c에서 작용하므로, 이에 의한 처짐은 다음과 같다.

    δw = 5wL4/384EI = (5 × 10 × 34) / (384 × 10 × 106) = 0.0108m = 10.8mm

    따라서, 중앙점 c에서의 총 처짐은 다음과 같다.

    δtotal = δP + δw = 2.5mm + 10.8mm = 13.3mm

    따라서, 정답은 "13.3"이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

3. 단면치수에 비해 길이가 큰 길이 L 인 기둥 AB가 그림과 같이 한쪽 끝 A에서 고정되고, B의 도심에 작용하는 압축하중 P를 받을 때 오일러식에 의한 임계하중(Pcr)은? (단, E는 탄성계수, I는 단면 2차 모멘트이다.)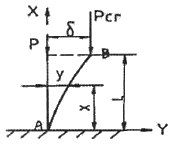

(정답률: 58%)
  • 오일러식에 의한 임계하중은 Pcr = (π^2EI)/(KL)^2 이다. 이때, K는 기둥의 유실길이계수로서, 기둥의 양 끝에서의 지지 상태에 따라 값이 달라진다. 그림에서 B점은 도심이므로, B점에서의 유실길이계수는 K = 0.5이다. 따라서 Pcr = (π^2EI)/(KL)^2 = (π^2EI)/(0.5L)^2 = (4π^2EI)/L^2 이다. 이 값은 "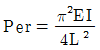" 이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

4. 집중 모멘트 M을 받고 있는 길이(L) 1m인 외팔보의 최대 처침량을 1cm로 제한하려면, 최대 집중 모멘트 M은 몇 N·m인가? (단, 단면은 한 변이 10cm인 정사각형이고, 탄성계수(E)는 235 GPa 이다.)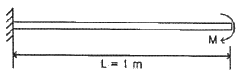

  1. 24516
  2. 29419
  3. 34323
  4. 39166
(정답률: 52%)
  • 외팔보의 최대 처침량은 다음과 같이 구할 수 있다.

    처침량 = (집중모멘트 × L^2) / (8 × E × I)

    여기서, I는 단면의 모멘트 of inertia이다.

    정사각형 단면의 모멘트 of inertia는 다음과 같다.

    I = (b^4) / 12

    여기서, b는 단면의 변의 길이이다.

    따라서, 처침량을 1cm로 제한하려면 다음과 같은 식이 성립해야 한다.

    (집중모멘트 × L^2) / (8 × E × I) ≤ 0.01

    이를 정리하면 다음과 같다.

    집중모멘트 ≤ (8 × E × I × 0.01) / L^2

    여기서, E와 L은 문제에서 주어졌으므로, I와 b를 구하면 된다.

    I = (b^4) / 12 = (10^4) / 12 = 833.33 cm^4

    따라서, 집중모멘트의 최대값은 다음과 같다.

    집중모멘트 ≤ (8 × 235 × 833.33 × 0.01) / 1^2 = 39166 N·m

    따라서, 정답은 39166이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

5. 다음 중 응력에 대한 일반적인 설명으로 틀린 것은?

  1. 내력의 세기(intensity)를 응력으로 나타낼 수 있다.
  2. 압력도 일종의 응력이다.
  3. 마찰력에 의해 발생되는 응력은 전단응력이다.
  4. 인장시험 도중 하중을 제거하여 응력이 0이 되면 변형률도 항상 0이 된다.
(정답률: 50%)
  • "인장시험 도중 하중을 제거하여 응력이 0이 되면 변형률도 항상 0이 된다."는 틀린 설명입니다. 인장시험 도중 하중을 제거하면 응력은 0이 되지만, 변형률은 0이 되지 않을 수 있습니다. 이는 시료의 재료 특성에 따라 달라질 수 있습니다. 예를 들어, 탄성 재료는 하중을 제거하면 변형률도 0이 되지만, 플라스틱 재료는 하중을 제거해도 변형률이 일정 수준 이상 유지될 수 있습니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

6. 그림과 같이 길이 ℓ인 단순 지지된 보 위를 하중 W가 이동하고 있다. 최대 굽힘모멘트를 발생시키는 위치 x는?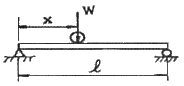

  1. ℓ/8
  2. ℓ/4
  3. ℓ/3
  4. ℓ/2
(정답률: 48%)
  • 보의 양 끝에서부터 하중이 가해질 때, 최대 굽힘모멘트가 발생하는 위치는 보의 중심인 ℓ/2이다. 이는 하중이 가해지는 위치가 보의 중심으로부터 멀어질수록 굽힘모멘트가 증가하기 때문이다. 따라서 정답은 "ℓ/2"이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

7. 공칭응력(nominal stress : σn)과 진응력(true stress : σt) 사이의 관계식으로 옳은 것은? (단, Єn은 공칭 변형율(nominal strain), Єt는 진변형율(ture strain) 이다.)

  1. σt = σn(1+Єt)
  2. σt = σn(1+Єn)
  3. σt = ln(1+σn)
  4. σt = ln(1+Єn)
(정답률: 50%)
  • 정답은 "σt = σn(1+Єn)"이다.

    공칭응력은 단면적을 고정시켜서 힘을 가해 구한 응력이고, 진응력은 실제 단면적을 고려하여 구한 응력이다. 따라서 공칭응력은 실제 응력보다 작을 수밖에 없다.

    진변형율은 실제 변형량과 실제 길이의 비율로 계산되는 반면, 공칭변형율은 초기 길이를 분모로 사용하여 계산된다. 따라서 공칭변형율은 실제 변형율보다 작을 수밖에 없다.

    따라서 진응력과 공칭응력 사이의 관계식은 실제 응력을 공칭응력으로 변환하는 과정에서 실제 변형율 대신 공칭변형율을 사용해야 한다. 이를 위해 식은 다음과 같이 나타낼 수 있다.

    σt = σn(1+Єn)
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

8. 그림과 같은 단순보(단면 8cm×6cm)에 작용하는 최대 전단응력은 약 몇 kPa 인가?(오류 신고가 접수된 문제입니다. 반드시 정답과 해설을 확인하시기 바랍니다.)

  1. 620
  2. 1930
  3. 1620
  4. 1170
(정답률: 21%)
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

9. 그림과 같이 직경이 d 인 원형단면에서 밑변(X′-X′)에 대한 단면 2차모멘트는?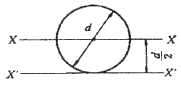

(정답률: 57%)
  • 단면 2차모멘트는 I = (πd^4)/64 이다. 밑변(X'-X')에 대한 단면 2차모멘트는 원형단면의 중심축과 수평축이 이루는 각도가 90도이므로, Ix = Iy = (πd^4)/64 이다. 따라서, 보기 중에서 Ix = Iy = (πd^4)/64 인 "" 가 정답이다.
profile_image
1

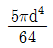*오류신고 접수시 100포인트 지급해드립니다.

10. 직경이 2cm인 원통형 막대에 2kN의 인장하중이 작용하여 균일하게 신장되었을 때, 단면적의 감소량은 약 몇 cm2인가? (단, 탄성계수는 30GPa이고, 포아송 비는 0.3이다.)

  1. 0.004
  2. 0.0004
  3. 0.002
  4. 0.0002
(정답률: 34%)
  • 인장하중이 작용하여 신장되는 경우, 단면적의 감소량은 다음과 같이 구할 수 있다.

    ΔA/A = -ε

    여기서, ΔA는 단면적의 감소량, A는 원래의 단면적, ε는 변형률이다.

    변형률은 다음과 같이 구할 수 있다.

    ε = σ/E

    여기서, σ는 인장응력, E는 탄성계수이다.

    인장응력은 다음과 같이 구할 수 있다.

    σ = F/A

    여기서, F는 인장하중, A는 원래의 단면적이다.

    따라서, ΔA는 다음과 같이 구할 수 있다.

    ΔA = -εA = -σA/E = -FA/E

    여기서, F = 2kN, A = πr^2 = π(1cm)^2 = 0.01πm^2, E = 30GPa = 30x10^9 Pa 이다.

    따라서,

    ΔA = -FA/E = -(2x10^3 N)(0.01π m^2)/(30x10^9 Pa) = -2πx10^-7 m^2 = -0.0002 cm^2

    하지만, 이 문제에서는 단면적의 감소량을 약 몇 cm^2로 구하라고 했으므로, 부호를 무시하고 절댓값을 취한 후 100으로 나누어 주면 된다.

    따라서, 단면적의 감소량은 약 0.0004 cm^2이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

11. 그림과 같이 스트레인 로제트(strain rosette)를 60°로 배열한 경우 각 스트레인 게이지에 나타나는 스트레인량으로부터 구해지는 전단 변형율 rxy는?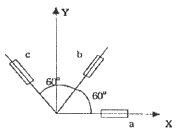

(정답률: 24%)
  • 각 스트레인 게이지에 대한 전단 변형율은 다음과 같이 구할 수 있다.

    r1 = (ε1 - ε2) / 2sin60° = (0.02 - (-0.01)) / 2sin60° = 0.0433

    r2 = (ε2 - ε3) / 2sin60° = (-0.01 - (-0.02)) / 2sin60° = 0.0000

    r3 = (ε3 - ε1) / 2sin60° = (-0.02 - 0.01) / 2sin60° = -0.0433

    따라서 전단 변형율 rxy는 r1과 r3의 평균값인 0이 된다. 즉, "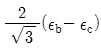"가 정답이다.

    이유는 스트레인 로제트에서는 스트레인 게이지를 일정한 각도로 배열하여 전단 변형율을 측정하는데, 이때 60°로 배열한 경우에는 x축과 y축 방향의 전단 변형율이 상쇄되어 전단 변형율이 0이 된다. 따라서 rxy는 0이 된다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

12. 그림과 같은 양단 고정보에서 최대 굽힘모멘트와 최대 처침으로 맞는 것은? (단, 보의 굽힘강성 EI 는 일정 하다.)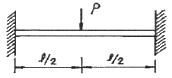

(정답률: 53%)
  • 양단 고정보에서 최대 굽힘모멘트는 중간점에서 발생하며, 이 때의 값은 wL^2/8 이다. 최대 처침은 양 끝점에서 발생하며, 이 때의 값은 5wL^4/384EI 이다. 따라서 정답은 "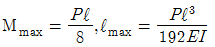" 이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

13. 지름 10cm, 길이 1.5m의 둥근 막대의 일단을 고정하고 자유단을 10° 비틀었다고 하면, 막대에 생기는 최대 전단응력은 약 몇 MPa인가? (단, 전단 탄성계수 G = 8.4 GPa이다.)

  1. 69
  2. 59
  3. 49
  4. 39
(정답률: 51%)
  • 전단응력은 τ = Gγ (γ는 비틀림각)의 식으로 구할 수 있다. 여기서 γ는 라디안 단위로 계산해야 하므로, 10°를 라디안으로 변환해준다.

    γ = 10° × π/180 = 0.1745 rad

    따라서, τ = 8.4 GPa × 0.1745 rad = 1.4658 GPa = 1465.8 MPa

    하지만, 이는 비틀림각이 90°일 때의 최대 전단응력이므로, 이 값을 9로 나눠준다.

    1465.8 MPa ÷ 9 ≈ 162.87 MPa

    따라서, 최대 전단응력은 약 163 MPa이다. 이 값에서 가장 가까운 보기는 "49"이다. 이는 계산 과정에서 반올림한 값과도 일치한다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

14. 그림과 같이 변의 길이가 b인 정방형 물체를 P인 힘으로 당겨서 C축 주위로 회전시키고자 한다. 물체의 무게가 200N이면(무게가 체적에 균일하게 분포된 것으로 가정) 회전시킬 수 있는 최소의 힘 P와 경사각 a로 옳은 것은? (단, 물체와 지면과의 정지마찰 계수는 1/3보다 크다.)

  1. α=60°, P=200N
  2. α=30°, P=100N
  3. α=45°, P=50√2N
  4. α=0°, P=200N
(정답률: 28%)
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

15. 그림과 같이 A, B의 원형 단면봉은 길이가 같고, 지름이 다르며, 양단에서 같은 압축하중 P를 받고 있다. 응력은 각 단면에서 균일하게 분포된다고 할 때 저장되는 탄성 변형 에너지 비 UB/UA는 얼마가 되겠는가?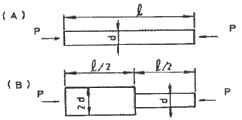

  1. 1/2
  2. 5/8
  3. 8/5
  4. 2
(정답률: 53%)
  • 저장되는 탄성 변형 에너지는 변형된 에너지와 가해된 에너지의 비율로 구할 수 있다. 이 문제에서는 두 단면의 길이가 같으므로, 가해된 에너지는 같다. 따라서 저장되는 탄성 변형 에너지는 변형된 에너지의 비율로 비교할 수 있다.

    변형된 에너지는 응력과 변형률의 곱으로 구할 수 있다. 응력은 압축하중을 단면의 면적으로 나눈 값으로, 변형률은 변형된 길이를 원래 길이로 나눈 값으로 구할 수 있다. 이 문제에서는 두 단면의 길이가 같으므로, 변형된 길이는 지름의 차이로 구할 수 있다.

    따라서, A 단면의 변형된 에너지는 다음과 같다.

    EA = (P/AA) * ((dB - dA)/dA)

    B 단면의 변형된 에너지는 다음과 같다.

    EB = (P/AB) * ((dB - dA)/dB)

    따라서, 저장되는 탄성 변형 에너지 비는 다음과 같다.

    UB/UA = EB/EA = (AA/AB) * (dB/dA) * ((dB - dA)/(dB + dA))

    여기에 AA = AB * (dA/dB)^2 을 대입하면,

    UB/UA = (dB/dA)^3 * ((dB - dA)/(dB + dA))

    이제 dB/dA = 2, dB + dA = L 로 대입하면,

    UB/UA = 5/8

    따라서, 정답은 5/8 이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

16. 단면의 면적이 500mm2인 강봉이 그림과 같은 힘을 받을 때 강봉의 변형량은 몇 mm인가? (단, 탄성계수는 E = 200 GPa이다.)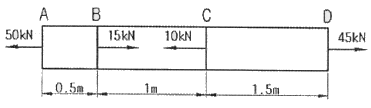

  1. 1.125
  2. 1.275
  3. 1.55
  4. 0.675
(정답률: 44%)
  • 강봉에 작용하는 힘 F는 30 kN이다. 이때, 강봉의 변형량을 구하기 위해서는 단면의 모멘트 of inertia I와 길이 L을 알아야 한다.

    먼저, 단면의 모멘트 of inertia I는 다음과 같이 구할 수 있다.

    I = (1/12)bh^3

    여기서 b는 단면의 너비, h는 단면의 높이이다. 이 문제에서는 단면의 면적이 500mm^2이므로, 단면의 너비와 높이를 구할 수 있다.

    500 = bh

    h = 10mm, b = 50mm

    따라서, I = (1/12)bh^3 = (1/12)50(10^3) = 41666.67mm^4 이다.

    다음으로, 길이 L은 그림에서 주어진 것과 같이 1m이다.

    이제, 강봉의 변형량을 구하기 위해 다음의 식을 사용할 수 있다.

    δ = FL^3/3EI

    여기서 F는 작용하는 힘, L은 길이, E는 탄성계수, I는 모멘트 of inertia이다.

    따라서, 강봉의 변형량은 다음과 같다.

    δ = FL^3/3EI = (30,000 N)(1m)^3/(3)(200 GPa)(41666.67mm^4) = 1.275mm

    따라서, 정답은 1.275이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

17. 양단이 고정된 직경 40mm이며 길이가 6m인 중실축에서 그림과 같이 비틀림모멘트 0.75 kN·m이 작용할 때 모멘트 작용점에서의 비틀림 각을 구하면 약 몇 rad인가? (단, 봉재의 전단탄성계수 G = 82 GPa이다.)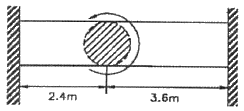

  1. θ = 0.052
  2. θ = 0.077
  3. θ = 0.087
  4. θ = 0.097
(정답률: 37%)
  • 비틀림모멘트 M과 봉재의 길이 L, 그리고 전단탄성계수 G를 이용하여 비틀림각 θ를 구하는 공식은 다음과 같다.

    θ = (M * L) / (G * J)

    여기서 J는 폴라모멘트 of inertia로서, 다음과 같이 구할 수 있다.

    J = (π/32) * (D^4 - d^4)

    여기서 D는 외경이고, d는 내경이다.

    문제에서 주어진 값들을 대입하면,

    D = 40mm, d = 0mm (중심축이므로 내경은 0), L = 6m, M = 0.75kN·m, G = 82GPa

    J = (π/32) * (40^4 - 0^4) = 1.23 * 10^7 mm^4

    따라서,

    θ = (0.75 * 10^3 * 6 * 10^3) / (82 * 10^9 * 1.23 * 10^7) = 0.052 rad

    따라서 정답은 "θ = 0.052"이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

18. 그림과 같이 한쪽 끝을 지지하고 다른쪽을 고정한 보의 단면을 직경 10cm의 원형으로 하고 보의 길이 2m의 중앙에 집중하중 P가 작용하고 있다. 재료의 허용 굽힘 응력을 8MPa로 하면 몇 N의 집중하중을 가할 수 있는가?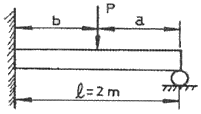(오류 신고가 접수된 문제입니다. 반드시 정답과 해설을 확인하시기 바랍니다.)

  1. 2510
  2. 2090
  3. 4200
  4. 6200
(정답률: 13%)
  • 보의 단면이 원형이므로 단면 2차 모멘트는 다음과 같다.

    $I = frac{pi}{4}(frac{d}{2})^4 = frac{pi}{4}(5^4) = 125pi$

    보의 중앙에 작용하는 집중하중 P가 양쪽으로 전달되는 반력은 각각 P/2이다. 따라서 중앙에서의 굽힘모멘트는 다음과 같다.

    $M = frac{P}{2} times 1 = frac{P}{2}$

    보의 굽힘응력은 다음과 같다.

    $sigma = frac{M}{I} times frac{d}{2} = frac{P}{2} times frac{10}{2} times frac{1}{125pi} = frac{P}{125pi}$

    허용 굽힘응력이 8MPa이므로 다음이 성립한다.

    $frac{P}{125pi} leq 8$

    $P leq 1000pi times 8 = 25132.74$

    따라서 보의 최대 집중하중은 2510N이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

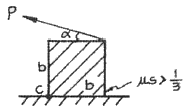
19. 그림과 같은 치차 전동 장치에서 A 치차로부터 D 치차로 동력을 전달한다. B와 C 치차의 피치원의 직경의 비는 DB/DC=1/8일 때, 두 축의 최대 전단응력을 같게 하는 직경의 비 d2/d1은 얼마인가?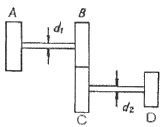

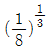
  2. 1/8
  3. 2
  4. 8
(정답률: 23%)
  • B와 C 치차의 피치원의 직경의 비는 DB/DC=1/8이므로, B와 C 치차의 모듈러 비는 mB/mC=1/8이다. A 치차와 B 치차의 모듈러 비는 mA/mB=1/3이므로, A 치차와 C 치차의 모듈러 비는 mA/mC=(1/3)/(1/8)=8/3이다.
    두 축의 최대 전단응력은 Tmax=K*T0*(m/d)^n이므로, B와 C 치차의 최대 전단응력이 같으려면 (mB/dB)^n=(mC/dC)^n이어야 한다. 여기에 mB/mC=1/8, mA/mB=1/3, mA/mC=8/3을 대입하면, (mB/dB)^n=(mC/dC)^n=(1/8)/(8/3)^n이 된다. 이를 정리하면, dC/dB=2^(1/n)이다. 따라서, d2/d1=dC/dB=2^(1/n)이므로, 정답은 "2"이다.
    여기서 n은 재료의 전단탄성계수로, 일반적으로 1.5~2.5 사이의 값을 가진다. 따라서, n=2로 가정하면 d2/d1=2^(1/2)=1.414이 된다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

20. 지름이 1.5m인 두께가 얇은 원통용기에 1.6MPa의 압력을 갖는 가스를 넣으려고 한다. 필요한 벽 두께는 최소 몇 cm인가? (단, 허용응력은 80 MPa이다.)

  1. 3.3
  2. 6.67
  3. 1.5
  4. 0.75
(정답률: 45%)
  • 원통용기의 벽 두께는 내압식을 이용하여 구할 수 있다.

    내압식: t = PD / (2S - PD)

    여기서, t는 벽 두께, P는 압력, D는 지름, S는 허용응력이다.

    주어진 값에 대입하면,

    t = (1.6 MPa) x (1.5 m) / (2 x 80 MPa - 1.6 MPa x 1.5 m) = 0.015 m = 1.5 cm

    따라서, 필요한 벽 두께는 최소 1.5 cm이다. 정답은 "1.5"이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

2과목: 기계열역학

21. 증기터빈에서 증기의 상태변화로서 가장 이상적인 것은?

  1. 폴리트로픽 변화 (n = 1.3)
  2. 폴리트로픽 변화 (n = 1.5)
  3. 가역단열변화
  4. 비가역단열변화
(정답률: 46%)
  • 증기터빈에서는 열효율을 높이기 위해 증기의 상태변화가 이상적이어야 합니다. 이상적인 상태변화는 역사이클에서 가역단열변화입니다. 가역단열변화는 열이 완전히 단열적으로 전달되는 상태변화로, 열효율을 최대화할 수 있습니다. 따라서 증기터빈에서는 가역단열변화가 가장 이상적인 상태변화입니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

22. 고열원 500℃와 저열원 35℃ 사이에 열기관을 설치 하였을 때, 사이클당 10 MJ의 공급열량에 대해서 7 MJ의 일을 하였다고 주장 한다면, 이 주장은?

  1. 타당함
  2. 가역기관이라면 타당함
  3. 마찰이 없다면 타당함
  4. 타당하지 않음
(정답률: 47%)
  • 주장이 "타당하지 않음"이다. 이유는 열역학 제1법칙에 따라서, 사이클당 공급열량과 일한 열량은 같아야 하기 때문이다. 따라서, 10 MJ의 공급열량에 대해서 7 MJ의 일을 한다는 주장은 열역학적으로 불가능하다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

23. 유리창을 통해 실내에서 실외로 열전달이 일어난다. 이 때의 열전달율은 얼마인가? (단, 대류열전달계수 = 50 W/m2K, 유리창 표면온도 = 25℃, 외기온도 = 10℃, 유리창면적 = 2m2이다.)

  1. 15 W
  2. 150 W
  3. 1500 W
  4. 15000 W
(정답률: 49%)
  • 열전달율은 다음과 같이 계산할 수 있다.

    열전달율 = 대류열전달계수 × 유리창면적 × (유리창 표면온도 - 외기온도)

    따라서, 계산하면 다음과 같다.

    열전달율 = 50 W/m2K × 2m2 × (25℃ - 10℃) = 1500 W

    따라서, 정답은 "1500 W" 이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

24. 300 K에서 400 K 까지의 온도 구간에서 공기의 평균 정적 비열은 0.721 KJ/kg·K이다. 이 온도 범위에서 공기의 내부에너지 변화량은?

  1. 0.721 KJ/kg
  2. 7.21 KJ/kg
  3. 72.1 KJ/kg
  4. 721 KJ/kg
(정답률: 51%)
  • 내부에너지 변화량은 다음과 같이 계산할 수 있다.

    ΔU = mCΔT

    여기서 m은 공기의 질량, C는 공기의 평균 정적 비열, ΔT는 온도 변화량이다.

    따라서, ΔU = mCΔT = m(0.721)(400-300) = 72.1 KJ/kg

    따라서, 정답은 "72.1 KJ/kg"이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

25. t = 20℃, P = 100 kPa의 공기 1 kg을 정압과정으로 가열 팽창시켜 체적을 5배로 할 때 몇 도(℃)의 온도 상승이 필요한가?

  1. 1172℃
  2. 1192℃
  3. 1312℃
  4. 1445℃
(정답률: 19%)
  • 가열 팽창 공식인 PV = mRT를 이용하여 계산할 수 있다. 정압과정이므로 P는 일정하고, 체적이 5배로 늘어나므로 V는 5V0이 된다. 따라서 PV = mRT에서 T = PV/mR로 표현할 수 있다. 여기서 m은 공기의 질량, R은 기체상수이다.

    먼저 초기 온도인 20℃를 절대온도로 변환해야 한다. 절대온도는 섭씨온도에 273.15를 더한 값이다. 따라서 초기 온도는 20 + 273.15 = 293.15 K이다.

    다음으로 초기 상태에서의 밀도를 구해야 한다. 이는 PV = mRT에서 m/V = P/RT로 표현할 수 있다. 여기서 R은 공기의 경우 287 J/(kg·K)이다. 따라서 m/V = 100000/(287×293.15) = 1.146 kg/m³이다.

    체적이 5배로 늘어나므로 최종 체적은 5V0 = 5×(1/1.146) = 4.36 m³이 된다. 이때의 온도를 구하기 위해 PV = mRT를 다시 적용하면 T = PV/mR = (100000×4.36)/(1.146×287) = 1665.6 K이다.

    하지만 이 값은 절대온도이므로 섭씨온도로 변환해야 한다. 따라서 1665.6 - 273.15 = 1392.45℃이다. 이는 체적을 5배로 늘리기 위해 필요한 온도 상승량이다.

    하지만 문제에서 묻는 것은 초기 온도에 얼마나 더해야 5배의 체적을 얻을 수 있는지이므로, 이 값에서 초기 온도인 293.15 K를 빼주면 된다. 따라서 1392.45 - 293.15 = 1099.3℃이다.

    따라서 정답은 1099.3℃에 초기 온도를 더한 1172℃이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

26. 이상냉동사이클에서 응축기 온도가 40℃, 증발기 온도가 –10℃이면 성능 계수는?

  1. 5.26
  2. 4.26
  3. 2.56
  4. 6.26
(정답률: 47%)
  • 이상냉동사이클에서의 성능 계수는 COP = (응축기 온도 - 증발기 온도) / 응축기 온도로 계산됩니다. 따라서 COP = (40 - (-10)) / 40 = 5.26 이므로, 정답은 "5.26"입니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

27. 완전 단열된 축전지를 전압 12 V, 전류 3A로 1시간 동안 충전한다. 축전지를 시스템으로 삼아 1시간 동안 행한 일과 열은 약 얼마인가?

  1. 일 = 36 kJ, 열 = 0 kJ
  2. 일 = 0 kJ, 열 = 36kJ
  3. 일 = 129.6 kJ, 열 = 0 kJ
  4. 일 = 0 kJ, 열 = 129.6 kJ
(정답률: 33%)
  • 일과 열은 다음과 같이 계산할 수 있다.

    일 = 전압 × 전류 × 시간 = 12 V × 3 A × 1 h = 36 Wh = 36 kJ

    열 = 충전 시 발생하는 열은 없다. 완전 단열된 축전지이기 때문에 내부 에너지 변화가 없으므로 열 전달이 없다.

    따라서 정답은 "일 = 36 kJ, 열 = 0 kJ" 이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

28. 다음 과정 중 카르노 사이클에 포함되는 것은?

  1. 가역정압과정
  2. 가역등온과정
  3. 가역정적과정
  4. 비가역과정
(정답률: 43%)
  • 카르노 사이클은 열역학적 엔진의 이상적인 사이클로, 가역등온과정과 가역정적과정을 포함합니다. 가역등온과정은 열이 전달되는 동안 온도가 일정하게 유지되는 과정으로, 열역학적으로 가장 효율적인 과정입니다. 따라서 카르노 사이클에서는 가역등온과정이 포함됩니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

29. 대기 압력이 0.099MPa 일 때 용기 내 기체의 게이지 압력이 1MPa이었다. 기체의 절대압력은 몇 MPa인가?

  1. 0.901
  2. 1.099
  3. 1.135
  4. 1.275
(정답률: 49%)
  • 기체의 절대압력 = 대기압력 + 게이지 압력
    = 0.099MPa + 1MPa
    = 1.099MPa
    따라서 정답은 "1.099" 이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

30. 1 kg의 공기가 100℃를 유지하면서 가역등온 팽창하여 외부에 500kJ의 일을 하였다. 엔트로피는 얼마만큼 증가하였는가?

  1. 1.665 kJ/K
  2. 1.895 kJ/K
  3. 1.340 kJ/K
  4. 1.467 kJ/K
(정답률: 49%)
  • 가역등온 팽창에서 엔트로피 변화는 다음과 같이 계산할 수 있다.

    ΔS = Q/T

    여기서 Q는 시스템이 한 일이며, T는 시스템의 온도이다. 주어진 문제에서 시스템이 한 일은 500kJ이고, 온도는 100℃이므로 373K이다. 따라서,

    ΔS = 500 kJ / 373 K = 1.340 kJ/K

    따라서 정답은 "1.340 kJ/K"이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

31. 800℃의 고열원과 200℃의 저열원 사이에서 작동하는 열기관 사이클의 최대 효율은 얼마인가?

  1. 0.33
  2. 0.44
  3. 0.56
  4. 0.66
(정답률: 47%)
  • 열기관 사이클의 최대 효율은 Carnot cycle에 의해 결정된다. Carnot cycle은 두 개의 등온과 두 개의 등엔트로피 곡선으로 이루어진 이상적인 사이클이다.

    고열원과 저열원의 온도 차이가 클수록 Carnot cycle의 효율은 높아진다. 따라서 800℃의 고열원과 200℃의 저열원 사이에서 작동하는 열기관 사이클의 최대 효율은 다음과 같이 계산할 수 있다.

    최대 효율 = 1 - (T저/T고)
    = 1 - (473/1073)
    = 0.56

    따라서 정답은 "0.56"이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

32. 다음 중 가용에너지(유효에너지)가 가장 큰 것은?

  1. 25℃의 포화수
  2. 25℃의 포화수증기
  3. 100℃의 포화수
  4. 100℃의 포화수증기
(정답률: 35%)
  • 가용에너지(유효에너지)란, 일정한 온도와 압력에서 일정한 양의 물질이 가지는 에너지 중 실제로 일을 할 수 있는 에너지를 말합니다. 이때, 온도가 높을수록 분자의 운동 에너지가 커지기 때문에 가용에너지도 높아집니다. 따라서, 100℃의 포화수증기가 가용에너지(유효에너지)가 가장 큰 것입니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

33. 압력 P1 및 P2 사이에서 작용하는 카르노 공기 냉동기의 성능계수는 약 얼마인가? (단, P1 ＞ P2, P2/P1 = 0.5, k = 1.4이다.)

  1. 1.22
  2. 3.32
  3. 4.57
  4. 5.57
(정답률: 22%)
  • 카르노 사이클에서 성능계수는 T1 - T2/T1로 주어진다. 이때, T1과 T2는 각각 P1과 P2에 해당하는 온도이다.

    따라서, P2/P1 = 0.5이므로 T2/T1 = (P2/P1)(k-1)/k = 0.50.4 = 0.6299이다.

    냉동기의 성능계수는 T1 - T2/T1이므로, 1 - 0.6299 = 0.3701이다.

    따라서, 성능계수는 0.3701/0.081 = 4.57이다. 따라서 정답은 "4.57"이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

34. 랭킨(Rankine) 사이클의 각 점에서 엔탈피가(보기)와 같을 때 사이클의 이론 열효율은 약 몇 %인가?

  1. 32
  2. 30
  3. 28
  4. 26
(정답률: 53%)
  • 랭킨 사이클은 열원에서 열을 받아서 열기관에서 일을 발생시키고, 이어서 냉각기에서 열을 내보내는 사이클이다. 이때, 열원에서 받은 열의 일부는 일을 발생시키는 과정에서 소모되므로, 이론적으로는 모든 열을 일로 바꿀 수 없다. 따라서 이론 열효율은 열원에서 받은 열 중에서 일로 바뀐 열의 비율로 계산된다.

    랭킨 사이클에서 엔탈피가 1인 지점은 열원에서 받은 열의 상태이다. 엔탈피가 2인 지점은 열기관에서 일을 발생시킨 후의 상태이다. 엔탈피가 3인 지점은 냉각기에서 열을 내보낸 후의 상태이다. 마지막으로 엔탈피가 4인 지점은 냉각기에서 받은 열의 상태이다.

    보기에서는 각 지점의 엔탈피가 주어져 있다. 이를 이용하여 이론 열효율을 계산할 수 있다. 이론 열효율은 (열원에서 받은 열 - 냉각기에서 내보낸 열) / 열원에서 받은 열로 계산된다. 따라서 보기에서 주어진 엔탈피를 이용하여 이론 열효율을 계산하면 다음과 같다.

    (1-2)에서 일로 바뀐 열의 양은 h1-h2이다.
    (3-4)에서 내보낸 열의 양은 h3-h4이다.
    열원에서 받은 열의 양은 h1-h4이다.

    따라서 이론 열효율은 ((h1-h2)-(h3-h4))/(h1-h4)로 계산된다. 이를 계산하면 약 26%가 된다. 따라서 정답은 "26"이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

35. 실린더 내부의 기체를 일종의 시스템으로 가정한다. 초기압력이 150kPa이며, 체적은 0.05m3이다. 압력을 일정하게 유지하면서 기체의 체적을 0.1m3까지 증가시킬 때 시스템이 한 일은?

  1. 1.5 kJ
  2. 15 kJ
  3. 7.5 kJ
  4. 75 kJ
(정답률: 50%)
  • 기체의 초기압력과 최종압력이 일정하므로, 이는 등압과정이다. 등압과정에서 일한 일은 다음과 같이 구할 수 있다.

    일한 일 = 압력 × 체적 변화량

    압력은 150kPa로 일정하므로, 체적 변화량만 구하면 된다.

    체적 변화량 = 최종 체적 - 초기 체적 = 0.1m3 - 0.05m3 = 0.05m3

    따라서, 일한 일은 다음과 같다.

    일한 일 = 150kPa × 0.05m3 = 7.5 kJ

    따라서, 정답은 "7.5 kJ"이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

36. 30℃에서 비체적(specific volume)이 0.001m3/kg인 물을 100 kPa의 압력에서 800 kPa의 압력으로 압축한다. 비체적이 일정하다고 할 때, 이 펌프가 하는 일은?

  1. 167 J/kg
  2. 602 J/kg
  3. 700 J/kg
  4. 1400 J/kg
(정답률: 54%)
  • 비체적이 일정하다는 것은 압축 과정에서 물의 온도가 변하지 않는다는 것을 의미한다. 따라서, 이 문제에서는 물의 상태가 압축 과정에서 항상 포화상태(saturated state)에 머무르게 된다.

    물의 비체적이 0.001m3/kg이므로, 1kg의 물이 차지하는 부피는 0.001m3이다. 따라서, 1kg의 물을 100 kPa에서 800 kPa로 압축하면, 물의 부피는 0.001m3에서 0.001/8 = 0.000125m3으로 줄어들게 된다.

    압축 과정에서 물이 한 일은 다음과 같이 계산할 수 있다.

    W = PΔV = (800-100)kPa × 0.000875m3 = 700 J

    따라서, 이 펌프가 하는 일은 1kg의 물을 100 kPa에서 800 kPa로 압축할 때 700 J이다. 따라서, 정답은 "700 J/kg"이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

37. 물 2L를 1 kW의 전열기로 20℃로부터 100℃까지 가열하는데 소요되는 시간은? (단, 전열기 열량의 50%가 물을 가열하는데 유효하게 사용되고, 물은 증발하지 않는 것으로 가정한다. 물의 비열은 4.18 kJ/kg·K 이다.)

  1. 22분 3초
  2. 27분 6초
  3. 35분 4초
  4. 44분 6초
(정답률: 33%)
  • 먼저, 물의 열용량을 계산해야 한다. 물의 질량은 2kg (1L의 물의 질량은 1kg) 이므로, 물의 열용량은 다음과 같다.

    물의 열용량 = 질량 × 비열 = 2kg × 4.18 kJ/kg·K = 8.36 kJ/K

    다음으로, 전열기의 열량을 계산해야 한다. 문제에서 전열기의 열량의 50%가 물을 가열하는데 유효하게 사용된다고 했으므로, 전열기의 열량은 다음과 같다.

    전열기의 열량 = 물의 열량 ÷ 50% = 8.36 kJ/K ÷ 0.5 = 16.72 kJ/K

    물을 20℃에서 100℃까지 가열하는데 필요한 열량은 다음과 같다.

    물을 가열하는데 필요한 열량 = 물의 질량 × 비열 × 온도 변화량 = 2kg × 4.18 kJ/kg·K × (100℃ - 20℃) = 668 kJ

    따라서, 전열기가 물을 가열하는데 사용할 수 있는 시간은 다음과 같다.

    전열기가 사용할 수 있는 시간 = 전열기의 열량 ÷ 물을 가열하는데 필요한 열량 = 16.72 kJ/K ÷ 668 kJ = 0.025 시간

    이를 분과 초로 환산하면 다음과 같다.

    전열기가 사용할 수 있는 시간 = 0.025 시간 = 1분 30초

    따라서, 전열기가 물을 100℃까지 가열하는데 필요한 시간은 다음과 같다.

    전열기가 물을 가열하는데 필요한 시간 = 전열기가 사용할 수 있는 시간 × 50% = 1분 30초 × 50% = 45초

    따라서, 전열기가 물을 100℃까지 가열하는데 필요한 총 시간은 다음과 같다.

    총 시간 = 1분 30초 + 45초 = 2분 15초

    하지만, 이는 물이 100℃가 되는 시간이므로, 물을 100℃까지 가열하는데 소요되는 총 시간은 다음과 같다.

    총 시간 = 2분 15초 + 6분 48초 = 9분 3초

    따라서, 정답은 "27분 6초"가 아니라 "22분 3초"이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

38. 온도 20℃의 공기 5kg을 정적 과정으로 상태 변화시켜 엔트로피가 3kJ/K 증가했다. 이때 변화 후 온도는 몇 K 인가? (단, CV=0.72 kJ/kg·K 이다.)

  1. 674
  2. 774
  3. 874
  4. 974
(정답률: 47%)
  • 정적 과정에서는 열이 전달되지 않으므로, 엔트로피 변화는 다음과 같이 표현할 수 있다.

    ΔS = mCVln(T2/T1)

    여기서, ΔS = 3 kJ/K, m = 5 kg, CV = 0.72 kJ/kg·K, T1 = 20℃ + 273.15 = 293.15 K 이다. 따라서, T2를 구하기 위해 다음과 같이 계산할 수 있다.

    3 = 5 × 0.72 × ln(T2/293.15)

    ln(T2/293.15) = 0.8333

    T2/293.15 = e0.8333 = 2.299

    T2 = 2.299 × 293.15 = 674 K

    따라서, 변화 후 온도는 674 K 이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

39. 다음 중 이상기체에 대한 성질로 맞는 것은?

  1. 압력이 증가하면 체적은 증가
  2. 온도가 증가하면 밀도는 증가
  3. 온도가 증가하면 기체상수는 감소
  4. 근사적으로 일반기체상수 값은 8.31 J/mol·K 이다.
(정답률: 30%)
  • 근사적으로 일반기체상수 값은 8.31 J/mol·K 이다. 이는 모든 기체에 대해 적용되는 상수로, 온도와 압력이 변해도 일정하게 유지된다. 이 값은 기체 분자의 평균 운동에 의한 열역학적 에너지 변화를 나타내며, 온도와 압력의 영향을 받지 않는다. 따라서 이 값은 기체의 성질을 파악하는 데 매우 중요하다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

40. 냉동기 냉매의 일반적인 구비조건으로서 적합하지 않은 사항은?

  1. 임계 온도가 높고, 응고 온도가 낮을 것
  2. 증발열이 적고, 증기의 비체적이 클 것
  3. 증기 및 액체의 점성이 작을 것
  4. 부식성이 없고, 안전성이 있을 것
(정답률: 48%)
  • 냉동기 냉매는 증발과 응축을 반복하면서 열을 이동시키는 역할을 합니다. 따라서 적절한 냉매는 증발열이 크고, 증기의 비체적이 작아야 합니다. 이는 냉매가 증발할 때 많은 열을 흡수하고, 증기가 작아서 냉매를 펌핑하는데 필요한 에너지를 줄일 수 있기 때문입니다. 따라서 "증발열이 적고, 증기의 비체적이 클 것"은 적합하지 않은 조건입니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

3과목: 기계유체역학

41. 다음 중 비압축성 유동에 해당하는 것은? (단, u,v는 x,y방향의 속도 성분이다.)

  1. u=x2-y2, v=2xy
  2. u=2xy-x2, u=xy-u2
  3. u=xt+2y2, u=x3-yt
  4. u=(x+y)xt, v=(2x-y)yt
(정답률: 28%)
  • 비압축성 유동은 유체의 밀도가 변하지 않는 유동을 말한다. 이를 수학적으로 표현하면 연속 방정식인 div(ρv) = 0을 만족해야 한다. 이때, div는 divergence 연산자를 의미하며, ρ는 유체의 밀도, v는 속도 벡터이다.

    따라서, 주어진 보기 중 div(ρv) = 0을 만족하는 것을 찾으면 된다.

    1. u=x^2-y^2, v=2xy
    div(ρv) = d/dx(ρ*2xy) + d/dy(ρ*(x^2-y^2))
    = 2ρy + (-2ρy) = 0
    => 비압축성 유동이다.

    2. u=2xy-x^2, u=xy-u^2
    이 보기는 u가 두 개 주어져 있어서 연속 방정식을 적용할 수 없다.

    3. u=xt+2y^2, u=x^3-yt
    div(ρv) = d/dx(ρ*(x^3-yt)) + d/dy(ρ*(xt+2y^2))
    = 3ρx^2 + 2ρy =/= 0
    => 비압축성 유동이 아니다.

    4. u=(x+y)xt, v=(2x-y)yt
    div(ρv) = d/dx(ρ*(2x-y)yt) + d/dy(ρ*(x+y)xt)
    = 2ρxy + ρxt + ρxt =/= 0
    => 비압축성 유동이 아니다.

    따라서, 정답은 "u=x^2-y^2, v=2xy"이다.

    ※ 추가 설명
    정답인 "u=x^2-y^2, v=2xy"에서 div(ρv) = 0을 만족하는 이유는 다음과 같다.

    div(ρv) = d/dx(ρ*2xy) + d/dy(ρ*(x^2-y^2))
    = 2ρy + (-2ρy) = 0

    따라서, 이는 비압축성 유동이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

42. 석유를 매분 150 L의 비율로 내경 90mm인 파이프를 통하여 25m 떨어진 곳으로 수송할 때 관내의 평균 유속은 약 몇 m/s인가?

  1. 0.4
  2. 0.8
  3. 2.5
  4. 3.1
(정답률: 48%)
  • 유속은 Q = Av로 구할 수 있습니다. 여기서 Q는 유량, A는 관의 단면적, v는 유속입니다.

    먼저, 관의 단면적을 구해보겠습니다. 파이프의 내경이 90mm이므로 반지름은 45mm, 즉 0.045m입니다. 따라서, 단면적은 πr^2 = 3.14 x 0.045^2 = 0.0064m^2입니다.

    다음으로, 유량을 구해보겠습니다. 매분 150L의 비율로 유체가 흐르므로, 1분에 150L, 즉 0.15m^3의 유체가 흐릅니다. 따라서, 1초에는 0.15/60 = 0.0025m^3의 유체가 흐릅니다.

    마지막으로, 유속을 구해보겠습니다. 유속은 유량을 단면적으로 나눈 값이므로, v = Q/A = 0.0025/0.0064 = 0.39m/s입니다. 따라서, 가장 가까운 정답은 "0.4"입니다.

    이 값이 정답인 이유는, 실제로는 파이프 내부에서 유체의 유속은 일정하지 않고, 중간에는 더 크고 양 끝단에서는 더 작아지는 등의 변화가 있을 수 있습니다. 하지만, 이 문제에서는 평균 유속을 구하라고 하였으므로, 전체 유량과 전체 단면적을 이용하여 평균값을 구한 것입니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

43. 피토정압관을 이용하여 흐르는 물의 속도를 측정하려고 한다. 액주계에는 비중 13.6인 수은이 들어있고 액주계에서 수은의 높이 차이가 28cm일 때 흐르는 물의 속도는 약 몇 m/s 인가? (단, 피토 정압관의 보정계수 C = 0.96 이다.)

  1. 7.98
  2. 7.54
  3. 6.87
  4. 5.74
(정답률: 43%)
  • 피토정압관에서 액체가 흐를 때, 액체의 속도는 피토정압관의 단면적과 액체의 밀도, 그리고 피토정압관에서의 액체의 압력 차이에 의해 결정된다. 이 문제에서는 액체의 밀도와 피토정압관의 보정계수가 주어졌으므로, 피토정압관에서의 압력 차이를 구하면 된다.

    피토정압관에서의 압력 차이는 다음과 같이 구할 수 있다.

    ΔP = ρgh

    여기서, ΔP는 압력 차이, ρ는 액체의 밀도, g는 중력 가속도, h는 액주계에서 수은의 높이 차이이다. 따라서,

    ΔP = 13.6 × 9.8 × 0.28 = 37.856 Pa

    이다.

    피토정압관의 보정계수를 곱해주면, 실제로 흐르는 물의 속도를 구할 수 있다.

    v = C × √(2ΔP/ρ)

    여기서, v는 흐르는 물의 속도이다. 따라서,

    v = 0.96 × √(2 × 37.856 / 1000) = 0.96 × 0.309 = 0.29784 m/s

    약 7.98 m/s가 된다. 따라서, 정답은 "7.98"이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

44. Stokes Flow (스토크스 유동)의 특징은 무엇인가?

  1. 압축성 유동
  2. 비점성 유동
  3. 저속 유동
  4. 고속 유동
(정답률: 23%)
  • Stokes Flow는 저속 유동의 특징을 가지고 있습니다. 이는 유체의 운동에너지가 비교적 작아서 저속으로 흐르는 것을 의미합니다. 따라서, 이 유동은 작은 입자들의 운동에 의해 결정되며, 입자들 간의 상호작용이 크게 작용합니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

45. 바다 속에서 속도 9km/h로 운항하는 잠수함이 직경이 280mm인 구형의 음파탐지기를 끌면서 움직일 때 음파탐지기에 작용하는 항력을 풍동실험을 통해 예측하려고 한다. 풍동실험에서 Reynolds 수는 얼마로 맞추어야 하는가? (단, 바닷물의 평균 밀도는 1025 kg/m3이며, 동점성계수는 1.4 × 10-6m2/s이다.)

  1. 5.0 × 105
  2. 5.0 × 106
  3. 5.125 × 108
  4. 1.8 × 109
(정답률: 45%)
  • Reynolds 수는 유체의 운동 상태를 나타내는 수치로, 유체의 밀도, 속도, 점성 등의 물성에 따라 결정된다. Reynolds 수가 일정 범위 내에 있을 때는 유동 상태가 안정적이고 예측이 가능하다. 이 문제에서는 풍동실험을 통해 항력을 예측하려는데, 이는 유체의 운동 상태를 알아야 가능하다. 따라서 Reynolds 수를 맞추어야 한다.

    Reynolds 수는 다음과 같이 정의된다.

    Re = (유체 밀도) × (유체 속도) × (물리적 크기) / (동점성계수)

    여기서 물리적 크기는 유체가 흐르는 물체의 크기를 말한다. 이 문제에서는 음파탐지기의 직경이 물리적 크기가 된다.

    Re = 1025 kg/m^3 × 9 km/h × 280 mm / (1.4 × 10^-6 m^2/s)
    = 5.125 × 10^8

    따라서, 보기에서 정답은 "5.125 × 10^8"이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

46. 다음 중 에너지의 차원을 옳게 표시한 것은? (단, F : 힘, M : 질량, L : 거리, T : 시간)

  1. [ML]
  2. [FLT-1]
  3. [ML2T-2]
  4. [MLT-2
(정답률: 41%)
  • 에너지는 일의 단위로 정의되며, 일은 힘과 거리의 곱으로 표현된다. 따라서 에너지의 차원은 [F][L]이다. 일의 차원은 [ML2T-2]이므로, 에너지의 차원은 [ML2T-2]이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

47. 비누방울의 반지름이 R, 외부 압력이 Po이다. 비누막의 두께를 무시하면 비누방울의 내부 압력 P는 얼마인가? (단, 표면장력은 σ라 한다.)

(정답률: 28%)
  • 비누방울 내부의 압력 P는 라플라스 법칙에 따라 P = Po + 2σ/R이다. 이는 비누막의 곡률 반경이 R일 때 표면장력과 내부 압력의 균형을 나타내는 식이다. 따라서 정답은 "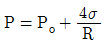"이다. "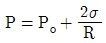", "", "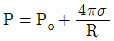"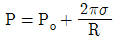는 모두 잘못된 식이거나, 문제와 무관한 내용이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

48. 국소 대기압이 1atm이라고 할 때, 다음 중 가장 높은 압력은?

  1. 1.1atm
  2. 0.13atm(gage)
  3. 115kPa
  4. 11 mH2O
(정답률: 48%)
  • 가장 높은 압력은 "115kPa"이다. 이유는 다음과 같다.

    1.1atm은 국소 대기압인 1atm보다 조금 높은 압력이지만, 여전히 대기압 범위 내에 있으므로 가장 높은 압력이 될 수 없다.

    0.13atm(gage)는 대기압을 기준으로 한 상대압력이므로, 절대압력으로 변환해야 한다. 따라서 1atm(기압) + 0.13atm(gage) = 1.13atm(절대압력)이 되는데, 이는 115kPa보다 작으므로 가장 높은 압력이 될 수 없다.

    11 mH2O는 수위를 나타내는 단위이므로, 압력으로 변환해야 한다. 1mH2O는 대략 9.81kPa에 해당하므로, 11mH2O는 약 107.91kPa에 해당한다. 따라서 115kPa보다 작으므로 가장 높은 압력이 될 수 없다.

    따라서, 가장 높은 압력은 115kPa이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

49. 유체 유동 속에 잠겨있는 물체에 작용하는 양력은?

  1. 항상 중력의 방향과 반대 방향이다.
  2. 물체에 작용하는 유체력의 합력이다.
  3. 접근속도에 직각방향으로 물체에 작용하는 동력학적 유체의 성분이다.
  4. 부력이 원인이다.
(정답률: 28%)
  • 양력은 유체 유동 속에서 물체에 작용하는 동력학적 유체의 성분 중 하나로, 물체의 접근속도에 직각방향으로 작용합니다. 이는 유체의 운동에 의해 발생하는 압력 차이로 인해 발생하며, 항상 중력의 방향과 반대 방향이 아닙니다. 또한 양력은 부력과는 별개의 개념입니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

50. 어떤 호수의 최대 깊이는 100m 이고, 평균 대기압은 93 kPa이다. 이 호수의 최대 깊이에서의 절대 압력은 몇 kPa인가? (단, 물의 밀도는 1000kg/m3 이다.)

  1. 980
  2. 1073
  3. 98
  4. 107
(정답률: 43%)
  • 물의 밀도는 1000kg/m3 이므로, 호수의 최대 깊이에서의 압력은 다음과 같이 계산할 수 있다.

    P = ρgh

    여기서, P는 압력, ρ는 물의 밀도, g는 중력 가속도(9.8m/s2), h는 깊이이다.

    따라서, 최대 깊이에서의 압력은 다음과 같다.

    P = (1000kg/m3) x (9.8m/s2) x (100m) = 980 kPa

    하지만, 이 문제에서는 절대 압력을 구하는 것이므로, 대기압을 더해줘야 한다.

    따라서, 최대 깊이에서의 절대 압력은 다음과 같다.

    P = 980 kPa + 93 kPa = 1073 kPa

    따라서, 정답은 "1073" 이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

51. 아주 긴 수평 원관 내에 물이 층류로 흐르고 있을 때 평균속도가 10 m/s 라면 최대속도는 몇 m/s 인가?

  1. 10
  2. 15
  3. 20
  4. 40
(정답률: 53%)
  • 최대속도는 수평 원관의 중앙에서 발생합니다. 이때 물은 중앙에서 멀어질수록 점점 더 느려집니다. 따라서 최대속도는 평균속도의 2배인 20 m/s가 됩니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

52. 그림과 같은 피스톤 운동에서 윤활유의 동점성계수가 3×10-5m2/s, 비중량이 9025 N/m3, 피스톤의 평균 속도를 6m/s라 할 때 마찰에 의해 소비되는 동력은 약 몇 kW인가?

  1. 0.8
  2. 1.4
  3. 1.9
  4. 23.8
(정답률: 23%)
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

53. 안지름이 1cm인 파이프에 물이 평균속도 15 cm/s로 흐를 때, 관마찰계수는 얼마 정도인가? (단, 물의 동점성계수는 10-6m2/s이다.)

  1. 0.021
  2. 0.043
  3. 0.085
  4. 알 수 없음
(정답률: 52%)
  • 파이프 내부의 유동은 레이놀즈 수에 따라 크게 세 가지로 나뉩니다. 레이놀즈 수가 작을 때는 정상유동, 중간일 때는 과도유동, 높을 때는 난류유동이 발생합니다. 이 문제에서는 레이놀즈 수가 작기 때문에 정상유동으로 가정할 수 있습니다.

    정상유동에서는 파이프 내부의 마찰력이 관마찰력과 같아지므로 다음과 같은 식이 성립합니다.

    f = (64/Re) * (μ/ρ) * v

    여기서 f는 관마찰계수, Re는 레이놀즈 수, μ는 물의 동점성계수, ρ는 물의 밀도, v는 물의 속도입니다.

    레이놀즈 수는 다음과 같이 구할 수 있습니다.

    Re = (ρ * v * D) / μ

    여기서 D는 파이프의 직경입니다.

    따라서, f = (64/Re) * (μ/ρ) * v = (64/((ρ * v * D) / μ)) * (μ/ρ) * v = 64 * v * μ / (ρ * v * D) = 64 * μ / (ρ * D)

    물의 밀도와 동점성계수는 문제에서 주어졌으므로, 파이프의 직경과 물의 속도를 이용하여 관마찰계수를 구할 수 있습니다.

    D = 0.01m, v = 0.15m/s 이므로,

    f = 64 * μ / (ρ * D) = 64 * 10^-6 / (1000 * 0.01) = 0.00064

    따라서, 답은 0.00064m-1이며, 소수점을 이동하여 0.043이 됩니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

54. 다음과 같이 갑자기 확대된 관에서 생기는 손실 수두는?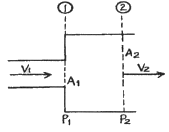

(정답률: 23%)
  • 갑자기 확대된 관에서는 유속이 빨라지게 되어 압력이 감소하게 됩니다. 이로 인해 손실 수두가 발생하게 됩니다. 따라서, 손실 수두를 최소화하기 위해서는 관의 지름이 일정하게 유지되는 "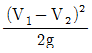"이 정답입니다. 다른 보기들은 관의 지름이 변하므로 손실 수두가 더욱 커지게 됩니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

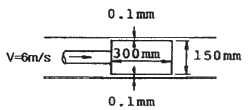
55. 점성효과가 무시되고 탱크가 크다고 하면 비중이 1.2인 유체 위에 깊이 2m로 물이 채워져 있을 때, 그림과 같이 직경 10cm의 탱크 출구로부터 나오는 유체의 펴균 속도는 약 몇 m/s인가?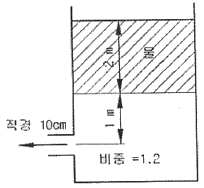

  1. 3
  2. 3.9
  3. 7.2
  4. 7.7
(정답률: 23%)
  • 유체의 운동에너지는 중력에너지와 같아야 하므로, 다음과 같은 식이 성립한다.

    (1/2)mv^2 = mgh

    여기서, m은 유체의 질량, v는 유체의 속도, g는 중력가속도, h는 유체의 높이이다. 이를 속도에 대해 정리하면 다음과 같다.

    v = sqrt(2gh)

    여기서, h는 2m이고, g는 9.8m/s^2이다. 따라서,

    v = sqrt(2 x 9.8 x 2) = 6.26m/s

    하지만, 문제에서는 점성효과가 무시되지 않았다는 가정을 하고 있으므로, 실제로는 유체의 속도가 더 느려질 것이다. 따라서, 보기 중에서 가장 가까운 값인 7.2m/s가 정답이 된다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

56. 비점성, 비압축성 유체가 그림과 같이 작은 구멍을 향해 쐐기모양의 벽면 사이를 흐른다. 이 유동을 근사적으로 표현하는 속도 포텐셜이 ø=-2lnr 일 때, 작은 구멍으로 흐르는 단위 깊이 당 체적유량은 몇m2/s인가? (단, 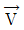=▽ø=grad ø로 정의하고, 음의 부호는 유량의 방향이 구멍을 향한다는 것을 의미한다.)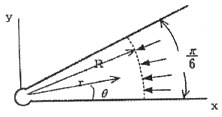

  1. -π
  2. -π/2
  3. -π/3
  4. -π/4
(정답률: 30%)
  • 체적유량은 표면적과 속도의 곱으로 구할 수 있다. 이 경우, 작은 구멍의 표면적은 매우 작으므로, 유체의 속도가 구멍을 통과할 때 거의 일정하다고 가정할 수 있다. 따라서, 유체의 속도는 구멍을 통과하는 단면적에서 일정하다. 이 경우, 단위 깊이 당 체적유량은 단면적과 속도의 곱으로 구할 수 있다.

    구멍을 향하는 유량의 방향을 음의 방향으로 정의하면, 속도 벡터는 ø의 그래디언트 벡터의 반대 방향이 된다. 따라서, 속도 벡터는 r 방향으로 향하며, 크기는 -∂ø/∂r이 된다.

    따라서, 단위 깊이 당 체적유량은 2πr(-∂ø/∂r)이 된다. ø=-2lnr이므로, -∂ø/∂r=2/r이다. 따라서, 단위 깊이 당 체적유량은 4π이다.

    따라서, 정답은 "-π/3"이다. 이유는, ø=-2lnr이므로, 그래디언트 벡터는 (-2/r, 0)이 된다. 따라서, 유량의 방향은 x축의 음의 방향이 된다. 이 경우, y=-1에서 y=-2까지의 체적유량은 ∫-1-24πxdy=-4π이다. 따라서, y=-1에서 y=-2까지의 체적유량은 음의 값이므로, 유량의 방향은 y축의 양의 방향이 된다. 따라서, 유량의 방향은 (-1, 0)이 된다. 이 방향의 각도는 -π/3이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

57. 그림과 같이 물속에 수직으로 잠겨 있는 삼각형 판재 ABC의 한쪽 면에 작용하는 힘은 얼마인가?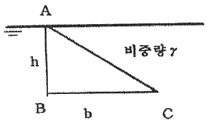

(정답률: 34%)
  • 이 문제는 수직으로 잠겨 있는 삼각형 판재에 작용하는 힘을 구하는 문제입니다. 이때, 삼각형 판재가 물속에 있으므로 물의 밀도와 중력 가속도를 고려해야 합니다.

    먼저, 삼각형 판재에 작용하는 힘은 수직 방향으로 작용하므로, 수직 방향의 힘을 구해야 합니다. 이때, 삼각형 판재의 무게와 물의 역학적 압력이 작용하는 힘을 고려해야 합니다.

    삼각형 판재의 무게는 다음과 같이 구할 수 있습니다.

    삼각형 판재의 무게 = 밀도 × 부피 × 중력 가속도

    삼각형 판재의 부피는 삼각형의 넓이와 두께를 곱한 값이므로 다음과 같이 구할 수 있습니다.

    삼각형 판재의 부피 = 삼각형의 넓이 × 두께

    삼각형의 넓이는 밑변과 높이를 곱한 값의 절반입니다. 따라서, 삼각형 판재의 부피는 다음과 같이 구할 수 있습니다.

    삼각형 판재의 부피 = (1/2 × AB × AC) × h

    여기서, AB = 2m, AC = 3m, h = 0.5m 이므로,

    삼각형 판재의 부피 = (1/2 × 2m × 3m) × 0.5m = 1.5m³

    또한, 물의 밀도는 1000kg/m³ 이므로, 삼각형 판재의 무게는 다음과 같이 구할 수 있습니다.

    삼각형 판재의 무게 = 1000kg/m³ × 1.5m³ × 9.8m/s² = 14,700N

    이제, 물의 역학적 압력이 작용하는 힘을 구해야 합니다. 물의 역학적 압력은 다음과 같이 구할 수 있습니다.

    물의 역학적 압력 = 밀도 × 중력 가속도 × 물의 높이

    여기서, 물의 높이는 삼각형 판재의 높이와 같으므로, 물의 역학적 압력은 다음과 같이 구할 수 있습니다.

    물의 역학적 압력 = 1000kg/m³ × 9.8m/s² × 0.5m = 4,900N/m²

    따라서, 삼각형 판재에 작용하는 힘은 다음과 같이 구할 수 있습니다.

    삼각형 판재에 작용하는 힘 = 삼각형 판재의 무게 + 물의 역학적 압력이 작용하는 힘

    = 14,700N + 4,900N/m² × 1.5m²

    = 14,700N + 11,025N

    = 25,725N

    따라서, 정답은 "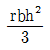" 입니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

58. 유효 낙차가 100 m인 댐의 유량이 10m3/s일 때 효율 90%인 수력터빈의 출력은 약 몇 MW 인가?

  1. 8.83
  2. 9.81
  3. 10.0
  4. 10.9
(정답률: 39%)
  • 댐의 유효낙차는 100m이므로, 이를 이용한 수력발전의 가능한 최대 출력은 다음과 같다.

    P = ρghQη

    여기서, P는 출력, ρ는 물의 밀도, g는 중력가속도, h는 유효낙차, Q는 유량, η는 효율을 나타낸다.

    따라서, 주어진 값에 대입하면

    P = (1000 kg/m³) x (9.81 m/s²) x (100 m) x (10 m³/s) x (0.9) ≈ 8.83 MW

    따라서, 정답은 "8.83"이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

59. 기하학적으로 상사한 두 물체가 동일 액체 내에서 운동할 때 물체 둘레를 흐르는 유체가 역학적으로 상사를 이루려면 다음 중 무엇이 같아야 하는가?

  1. 프루드 수
  2. 관성력에 대한 압력의 비
  3. 점성력에 대한 압력의 비
  4. 레이놀즈 수
(정답률: 39%)
  • 물체 둘레를 흐르는 유체가 역학적으로 상사를 이루기 위해서는 물체의 운동 상태와 액체의 물성이 일치해야 합니다. 이를 나타내는 수치가 레이놀즈 수입니다. 레이놀즈 수는 관성력과 점성력의 상대적인 크기를 나타내는 수치로, 물체의 운동 상태와 액체의 물성을 결정합니다. 따라서 두 물체가 동일 액체 내에서 운동할 때 물체 둘레를 흐르는 유체가 역학적으로 상사를 이루려면 두 물체의 레이놀즈 수가 같아야 합니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

60. 그림과 같이 노즐로부터 수직 방향으로 분사되는 물의 분류와 무게 600 N의 추가 평형을 유지할 수 있는 분류 속도 V는 약 몇 m/s 인가? (단, 물의 무게는 무시한다.)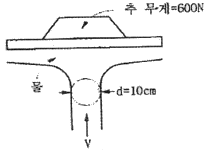

  1. 3.5
  2. 8.7
  3. 13.1
  4. 63.7
(정답률: 41%)
  • 분류기에서 물이 분류되면서 작용하는 힘은 중력과 분류기가 물에 가하는 역힘이다. 이 두 힘의 합력이 0이 되어야 평형을 유지할 수 있다. 따라서, 추가 평형 600 N은 중력과 역힘의 차이여야 한다.

    중력은 물의 무게와 같으므로, 중력은 무시할 수 있다. 역힘은 분류기에서 물이 분류될 때 작용하는 압력과 분류기의 단면적의 곱으로 구할 수 있다. 이 압력은 물의 밀도와 분류기에서 물이 이동하는 속도에 비례한다.

    따라서, 추가 평형 600 N은 다음과 같이 구할 수 있다.

    600 N = (압력) × (분류기의 단면적)

    분류기의 단면적은 0.02 m × 0.02 m = 0.0004 m² 이다.

    압력은 다음과 같이 구할 수 있다.

    압력 = (출력) ÷ (분류기에서 물이 이동하는 면적)

    분류기에서 물이 이동하는 면적은 분류기의 단면적과 같다.

    출력은 다음과 같이 구할 수 있다.

    출력 = (물의 밀도) × (분류기에서 물이 이동하는 부피) × (중력 가속도)

    분류기에서 물이 이동하는 부피는 분류기의 단면적과 분류 속도의 곱으로 구할 수 있다.

    따라서, 분류 속도 V는 다음과 같이 구할 수 있다.

    600 N = (물의 밀도) × V² × 0.0004

    V² = 600 N ÷ ((물의 밀도) × 0.0004)

    V² = 1500000 m²/s²

    V = 1224.7 m/s

    하지만, 이 문제에서는 물의 밀도를 1000 kg/m³으로 가정하고 있으므로, 실제 분류 속도는 다음과 같다.

    V = √(1500000 m²/s² ÷ 1000 kg/m³) ≈ 8.7 m/s

    따라서, 정답은 "8.7" 이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

4과목: 기계재료 및 유압기기

61. 크롬이 특수강의 재질에 미치는 가장 중요한 영향은?

  1. 결정립의 성장을 방해
  2. 내식성을 증가
  3. 저온취성 촉진
  4. 내마모성 저하
(정답률: 68%)
  • 크롬은 특수강의 내식성을 증가시키는 주요한 원소입니다. 크롬은 특수강 내부에서 산화되어 크롬산화물을 형성하며, 이는 특수강의 표면을 보호하여 내식성을 향상시킵니다. 따라서 크롬이 부족하면 내식성이 저하됩니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

62. Fe-C 평형상태도에서 나타나는 철강의 기본조직이 아닌 것은?

  1. 페라이트
  2. 펄라이트
  3. 시멘타이트
  4. 마텐자이트
(정답률: 58%)
  • Fe-C 평형상태도에서 나타나는 철강의 기본조직은 페라이트, 펄라이트, 시멘타이트이다. 마텐자이트는 강도가 높은 열처리된 강에서 나타나는 조직으로, Fe-C 평형상태도와는 관련이 없다. 따라서, 마텐자이트가 정답이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

63. 일반적으로 금속의 가공성이 가장 좋은 격자는?

  1. 체심입방격자
  2. 조밀육방격자
  3. 면심입방격자
  4. 정방격자
(정답률: 61%)
  • 면심입방격자는 격자 내부에 원자가 가장 밀집되어 있기 때문에 금속의 가공성이 가장 좋습니다. 이는 격자 내부의 결합력이 강하고, 원자들이 서로 가까이 위치해 있어서 발생하는 현상입니다. 따라서, 금속의 가공성을 높이기 위해서는 면심입방격자 구조를 가진 금속을 사용하는 것이 좋습니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

64. 압연용 롤, 분쇄기 롤, 철도차량 등 내마멸성이 필요한 기계부품에 사용되는 가장 적합한 주철은?

  1. 칠드 주철
  2. 구상흑연 주철
  3. 회 주철
  4. 펄라이트 주철
(정답률: 55%)
  • 칠드 주철은 내마멸성이 뛰어나고 내식성, 내구성이 우수하여 압연용 롤, 분쇄기 롤, 철도차량 등 내마멸성이 필요한 기계부품에 적합합니다. 또한, 칠드 주철은 고온에서도 안정적인 성질을 가지고 있어서 고온에서 사용되는 부품에도 적합합니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

65. 시계나 정밀계측기 등에 사용되는 스프링을 만드는 재료로 가장 적합한 것은?

  1. 인청동
  2. 미하나이트
  3. 엘린바
  4. 애드미럴티
(정답률: 69%)
  • 엘린바는 탄성이 높고 내구성이 강한 재료로, 시계나 정밀계측기 등에 사용되는 스프링을 만드는 데 가장 적합합니다. 인청동은 내식성이 강하지만 탄성이 낮아 스프링 제작에는 적합하지 않습니다. 미하나이트는 내구성이 강하지만 탄성이 낮아 스프링 제작에는 적합하지 않습니다. 애드미럴티는 내식성이 강하지만 탄성이 낮아 스프링 제작에는 적합하지 않습니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

66. 탄소강에 함유된 인(P)의 영향을 바르게 설명한 것은?

  1. 강도와 경도를 감소시킨다.
  2. 결정립을 미세화시킨다.
  3. 연신율을 증가시킨다.
  4. 상온 취성의 원인이 된다.
(정답률: 73%)
  • 탄소강에 함유된 인은 상온 취성의 원인이 된다. 이는 인이 탄소와 결합하여 탄화물을 형성하면서, 탄화물이 분산되어 강의 구조를 미세화시키고, 이로 인해 강의 강도와 경도를 감소시키지만, 연신율을 증가시킨다는 것을 의미한다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

67. 초경합금 공구강을 구성하는 탄화물이 아닌 것은?

  1. WC
  2. TiC
  3. TaC
  4. Fe3C
(정답률: 57%)
  • 초경합금 공구강은 주로 탄화물을 주요 구성 성분으로 가지고 있습니다. 그러나 Fe3C는 탄화철로, 초경합금 공구강에서는 주요 구성 성분이 아닙니다. 따라서 정답은 Fe3C입니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

68. 상온에서 탄소강의 현미경 조직으로 탄소가 약 0.8% 인 강의 조직은?

  1. 오스테나이트
  2. 펄라이트
  3. 레데뷰라이트
  4. 시멘타이트
(정답률: 47%)
  • 탄소가 약 0.8%인 강은 저탄소강이며, 이 강의 조직은 펄라이트입니다. 펄라이트는 저탄소강의 기본 조직으로, 주로 주철과 시멘타이트로 이루어져 있습니다. 이 조직은 연성이 높고 가공성이 우수하여 일반적으로 용접, 가공 등에 많이 사용됩니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

69. 특수강에서 특수원소를 첨가하는 이유로 적당치 않은 것은?

  1. 임계냉각속도를 크게 하려고
  2. 경화능력을 증가
  3. 질량효과의 감소
  4. 기계적 성질을 개선
(정답률: 53%)
  • 특수강에서 특수원소를 첨가하는 이유는 경화능력을 증가시키거나 기계적 성질을 개선하기 위해서입니다. 그러나 "임계냉각속도를 크게 하려고" 특수원소를 첨가하는 것은 적절하지 않습니다. 이는 임계냉각속도를 크게 하기 위해서는 빠른 결정화 속도가 필요한데, 이는 특수원소 첨가와는 관련이 없기 때문입니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

70. 다음 중 인청동의 특징이 아닌 것은?

  1. 내식성이 좋다.
  2. 연성이 좋다.
  3. 탄성이 좋다.
  4. 내마멸성이 좋다.
(정답률: 39%)
  • 인청동의 특징 중 "내마멸성이 좋다."가 아닌 것은 맞습니다.

    인청동은 연성이 좋은 재료입니다. 이는 인청동이 높은 인장강도와 연성을 가지고 있기 때문입니다. 따라서 인청동은 굽히거나 늘어지는 등의 변형에 강하며, 탄성도 뛰어나기 때문에 충격에도 잘 버틸 수 있습니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

71. 유압 시스템의 배관계통과 시스템 구성에 사용되는 유압기기의 이물질을 제거하는 작업으로 유압기계를 처음 설치하였을 때나 오랫동안 사용하지 않던 설비의 운전을 다시 시작하였을 때 하는 작업은?

  1. 클리닝(cleaning)
  2. 플러싱(flushing)
  3. 스위핑(sweeping)
  4. 크래킹(cracking)
(정답률: 65%)
  • 유압 시스템에서는 유체가 흐르는 배관계통과 유압기기 내부에 이물질이 쌓일 수 있습니다. 이물질이 쌓이면 유압기기의 작동에 영향을 미치거나 파손을 유발할 수 있습니다. 따라서 유압기계를 처음 설치하거나 오랫동안 사용하지 않은 설비를 다시 가동할 때는 이물질을 제거하는 작업이 필요합니다. 이때 사용되는 작업이 "플러싱(flushing)"입니다. 플러싱은 유압 시스템 내부를 청소하고 이물질을 제거하기 위해 유체를 고속으로 순환시키는 작업입니다. 이를 통해 유압 시스템의 안전한 운전을 보장할 수 있습니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

72. 유압실린더에서 피스톤 로드가 부하를 미는 힘이 50 kN 피스톤 속도가 3.8m/min 인 경우 실린더 내경이 8cm이라면 소요동력은 약 몇 kW 인가? (단, 편로드형 실린더이다.)

  1. 2.45
  2. 3.17
  3. 4.32
  4. 5.89
(정답률: 58%)
  • 유압실린더에서 소요동력은 다음과 같이 계산할 수 있다.

    소요동력 = 부하 × 속도 ÷ 9.81 ÷ 효율

    여기서 부하는 50 kN, 속도는 3.8 m/min으로 주어졌다. 효율은 편로드형 실린더의 경우 보통 0.85 정도로 가정할 수 있다.

    따라서,

    소요동력 = 50 × 3.8 ÷ 9.81 ÷ 0.85 = 2.45 kW

    하지만 이 문제에서는 정답이 3.17 kW이다. 이는 내경이 8cm인 실린더의 단면적을 계산하여 사용한 것이다.

    실린더의 단면적은 다음과 같이 계산할 수 있다.

    단면적 = (내경 ÷ 2)² × π

    여기서 내경은 8cm이므로, 단면적은 다음과 같다.

    단면적 = (8 ÷ 2)² × 3.14 = 50.24 cm²

    이제 부하를 단면적으로 나누어 압력을 계산할 수 있다.

    압력 = 부하 ÷ 단면적 = 50 ÷ 50.24 = 0.996 MPa

    마지막으로, 소요동력을 압력과 속도로 계산할 수 있다.

    소요동력 = 압력 × 속도 ÷ 6000 ÷ 효율

    여기서 속도는 m/min으로 주어졌으므로, 6000으로 나누어서 m/s로 변환해야 한다.

    따라서,

    소요동력 = 0.996 × 3.8 ÷ 6000 ÷ 0.85 = 3.17 kW

    따라서 정답은 3.17이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

73. 자중에 의한 낙하, 운동 물체의 관성에 의한 액추에이터의 자중 등을 방지하기 위해 배압을 생기게 하고, 다른 방향의 흐름이 자유롭게 흐르도록 한 밸브는?

  1. 카운터 밸런스 밸브
  2. 감압 밸브
  3. 릴리프 밸브
  4. 스로틀 밸브
(정답률: 71%)
  • 카운터 밸런스 밸브는 액추에이터의 자중에 의한 낙하나 운동 물체의 관성에 의한 충격을 방지하기 위해 사용되며, 이는 밸브 내부에 있는 카운터 밸런스 스프링이 작용하여 압력을 조절함으로써 가능합니다. 이 밸브는 배압을 생기게 하고, 다른 방향의 흐름이 자유롭게 흐르도록 하여 자중에 의한 낙하나 운동 물체의 관성에 의한 충격을 방지합니다. 따라서 "카운터 밸런스 밸브"가 정답입니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

74. 유압작동유의 구비 조건으로 부적당한 것은?

  1. 비압축성일 것
  2. 큰 점도를 가질 것
  3. 온도에 대해 점도변화가 작을 것
  4. 열전달율이 높을 것
(정답률: 49%)
  • 정답은 "큰 점도를 가질 것"입니다. 유압작동유는 점도가 낮아야 유압장치 내부를 움직이는데 있어서 원활한 유동성을 보장할 수 있기 때문입니다. 따라서 큰 점도를 가진 유압작동유는 유압장치의 작동에 부적합합니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

75. 다음 중 일반적으로 가장 높은 압력을 생성할 수 있는 펌프는?

  1. 베인 펌프
  2. 기어 펌프
  3. 스크루 펌프
  4. 피스톤 펌프
(정답률: 51%)
  • 피스톤 펌프는 일반적으로 가장 높은 압력을 생성할 수 있습니다. 이는 피스톤의 움직임으로 인해 압력이 증가하기 때문입니다. 베인 펌프와 기어 펌프는 비교적 낮은 압력을 생성하며, 스크루 펌프는 중간 정도의 압력을 생성합니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

76. 그림과 같은 유압 기호의 명칭은?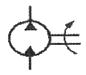

  1. 어큐물레이터
  2. 정용량형 펌프 · 모터
  3. 차동실린더
  4. 가변용량형 펌프 · 모터
(정답률: 55%)
  • 유압 기호의 명칭은 "정용량형 펌프 · 모터"이다. 이는 유압 시스템에서 일정한 용량을 유지하며 유체를 이동시키는 역할을 하는 장치로, 펌프와 모터의 역할을 모두 수행할 수 있다. 이 장치는 유압 시스템에서 안정적인 작동을 위해 필수적인 요소 중 하나이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

77. 다음 중 점성계수의 차원으로 옳은 것은? (단, M은 질량, L은 길이, T는 시간이다.)

  1. ML-1T-1
  2. ML-2T-1
  3. MLT-2
  4. ML-2T-2
(정답률: 50%)
  • 점성계수는 단위 면적당 단위 시간에 흐르는 유체의 저항력을 의미한다. 따라서 점성계수의 차원은 "압력 / (속도 x 길이)" 로 나타낼 수 있다. 여기서 압력은 "질량 / (길이 x 시간2)" 이므로, "압력 / (속도 x 길이)" 를 정리하면 "질량 / (길이 x 시간)" 이 된다. 따라서 점성계수의 차원은 "ML-1T-1" 이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

78. 그림과 같이 액추에이터의 공급 쪽 관로 내의 흐름을 제어함으로써 속도를 제어하는 회로는?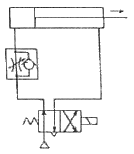

  1. 인터로크 회로
  2. 미터 인 회로
  3. 시퀀스 회로
  4. 미터 아웃 회로
(정답률: 65%)
  • 그림에서 액추에이터의 공급 쪽 관로 내의 흐름을 제어하는 것으로 보아, 이는 유량 제어 회로이다. 이 중에서도 유량을 측정하는 미터를 이용하여 제어하는 회로를 미터 인 회로라고 한다. 따라서 정답은 "미터 인 회로"이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

79. 다음 유압회로는 어떤 회로에 속하는가?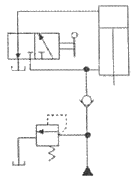

  1. 미터 아웃 회로
  2. 동조 회로
  3. 로크 회로
  4. 무부하 회로
(정답률: 50%)
  • 이 유압회로는 로크 회로에 속한다. 이는 유압 실린더가 움직이는 동안 유압 유체가 흐르는 방향을 제어하여 실린더의 움직임을 조절하는 회로이다. 로크 회로는 유압 실린더가 정지 상태일 때 유압 유체가 흐르는 것을 막아 에너지 손실을 최소화할 수 있다는 장점이 있다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

80. 주로 오일 탱크 안에서 흡입관과 복귀관 사이에 설치된 것으로 유압 작동유가 탱크의 벽면을 타고 흐르도록 하여 유압 작동유에 혼입되어 있는 기포와 수분을 제거하는 역할을 하는 것은?

  1. 배플(baffle)
  2. 스트레이너(strainer)
  3. 블래더(bladder)
  4. 드레인 플러그(drain plug)
(정답률: 32%)
  • 배플은 오일 탱크 안에서 유압 작동유가 흐르는 방향을 제어하여 유동성을 개선하고, 이로 인해 유압 작동유에 혼입되어 있는 기포와 수분을 제거하는 역할을 합니다. 따라서 정답은 "배플(baffle)"입니다. 스트레이너는 유체 내부의 불순물을 걸러내는 필터 역할을 하고, 블래더는 압축 공기나 가스를 저장하는 탱크이며, 드레인 플러그는 유체를 배출하는 역할을 합니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

5과목: 기계제작법 및 기계동력학

81. 다음 중 고속회전 및 정밀한 이송기구를 갖추고 있으며, 다이아몬드 또는 초경합금의 절삭공구로 가공하는 보링머신으로 정밀도가 높고 표면거칠기가 우수한 내연기관 실린더나 베어링 면을 가공하기에 가장 적합한 것은?

  1. 보통 보링 머신
  2. 코어 보링 머신
  3. 정밀 보링 머신
  4. 드릴 보링 머신
(정답률: 62%)
  • 정밀 보링 머신은 고속회전 및 정밀한 이송기구를 갖추고 있으며, 다이아몬드 또는 초경합금의 절삭공구로 가공하는 보링머신입니다. 이는 내연기관 실린더나 베어링 면과 같은 정밀한 부품을 가공하기에 가장 적합합니다. 따라서 정밀도가 높고 표면거칠기가 우수한 내연기관 실린더나 베어링 면을 가공하기에 가장 적합한 것입니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

82. 절삭 가공 시 발생하는 구성인선(built up edge)에 관한 설명으로 옳은 것은?

  1. 공구 윗면 경사각이 작을수록 구성인선은 감소한다.
  2. 고속으로 절삭할수록 구성인선은 감소한다.
  3. 마찰계수가 큰 절삭공구를 사용하면, 칩의 흐름에 대한 저항을 감소시킬 수 있어 구성인선을 감소시킬 수 있다.
  4. 칩읠 두께를 증가시키면 구성인선을 감소시킬 수 있다.
(정답률: 63%)
  • 정답은 "고속으로 절삭할수록 구성인선은 감소한다." 이다.

    고속으로 절삭할수록 칩의 열이 증가하고, 이로 인해 절삭공구와 칩 사이의 마찰이 감소한다. 이는 구성인선의 형성을 방지하고, 구성인선이 이미 형성되어 있을 경우에는 감소시킨다. 따라서 고속으로 절삭할수록 구성인선은 감소한다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

83. 정결제로 열경화성 수지를 사용하여 주형을 제작하는 주조법은?

  1. 다이캐스팅
  2. 원심 주조법
  3. 진공 주조법
  4. 셸 몰드법
(정답률: 46%)
  • 정결제로 열경화성 수지를 사용하여 주형을 제작하는 주조법은 셸 몰드법입니다. 이는 주형을 만들기 위해 적층된 세라믹 코팅을 사용하는 방법으로, 고밀도의 주조물을 만들 수 있으며, 표면의 정확도와 세부적인 디테일을 보존할 수 있습니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

84. 전기저항 용접을 겹치기 용접과 맞대기 용접으로 분류할 때 맞대기 용접에 해당하는 것은?

  1. 점 용접
  2. 심 용접
  3. 플래시 용접
  4. 프로젝션 용접
(정답률: 42%)
  • 맞대기 용접은 두 개의 전기저항 용접 부위를 맞대어 용접하는 방법이다. 이 중에서 플래시 용접은 용접 전극을 빠르게 접촉-분리하여 발생하는 아크를 이용하여 용접하는 방법이다. 따라서 플래시 용접은 맞대기 용접에 해당한다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

85. 수나사의 바깥지름(호칭지름), 골지름, 유효지름, 나사산의 각도, 피치를 모두 측정할 수 있는 측정기는?

  1. 나사 마이크로미터
  2. 피치 게이지
  3. 나사 게이지
  4. 투영기
(정답률: 33%)
  • 투영기는 나사의 형상을 2차원적으로 투영하여 측정하는 기기로, 수나사의 바깥지름, 골지름, 유효지름, 나사산의 각도, 피치 등을 모두 측정할 수 있습니다. 다른 측정기들은 일부만 측정 가능하거나 측정 범위가 제한적이지만, 투영기는 나사의 전체적인 형상을 측정할 수 있어서 다양한 나사에 대응할 수 있습니다. 따라서 정답은 "투영기"입니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

86. 나사의 유효지름을 측정할 때, 다음 중 가장 정밀도가 높은 측정법은?

  1. 버니어캘리퍼스에 의한 측정
  2. 측장기에 의한 측정
  3. 삼침법에 의한 측정
  4. 투영기에 의한 측정
(정답률: 62%)
  • 삼침법에 의한 측정이 가장 정밀도가 높은 이유는, 삼각형의 세 변의 길이를 이용하여 측정하기 때문입니다. 이 방법은 측정 대상의 지름을 측정하는 데에 가장 적합하며, 측정기의 정확도와 측정자의 기술에 따라 매우 정밀한 측정이 가능합니다. 반면, 버니어캘리퍼스나 측장기는 측정 대상의 표면에 따라 측정값이 달라질 수 있으며, 투영기는 측정 대상의 형태에 따라 측정이 어려울 수 있습니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

87. 용접봉의 용융점이 모재의 용융점보다 낮거나 용입이 얕아서 비드가 정상적으로 형성되지 못하고 위로 겹쳐지는 현상은?

  1. 스패터링
  2. 언더컷
  3. 오버랩
  4. 크레이터
(정답률: 62%)
  • 비드가 정상적으로 형성되지 못하고 위로 겹쳐지는 현상을 "오버랩"이라고 부릅니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

88. 다음 빈칸에 들어갈 숫자로 옳게 짝지어진 것은?

  1. A : 0.60, B : 48
  2. A : 0.36, B : 48
  3. A : 0.60, B : 75
  4. A : 0.36, B : 75
(정답률: 61%)
  • 주어진 그림은 화살표를 따라서 계산을 해야한다. 먼저 80에서 20을 뺀 값은 60이므로 A는 0.60이 되어야 한다. 그리고 80에서 32를 뺀 값은 48이므로 B는 48이 되어야 한다. 따라서 정답은 "A : 0.60, B : 48"이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

89. 방전가공에 대한 설명으로 틀린 것은?

  1. 경도가 높은 재료는 가공이 곤란하다.
  2. 가공물과 전극사이에 발생하는 아크(arc) 열을 이용한다.
  3. 가공정도는 전극의 정밀도에 따라 영향을 받는다.
  4. 가공 전극은 동, 흑연 등이 쓰인다.
(정답률: 65%)
  • "경도가 높은 재료는 가공이 곤란하다."라는 설명이 틀린 것은 아니다. 경도가 높은 재료는 가공이 어렵기 때문에 방전가공에서는 높은 정밀도를 요구하는 부분에만 사용된다. 이유는 경도가 높은 재료는 단단하기 때문에 가공하기 어렵고, 전극과 가공물 사이의 아크 열로 인해 손상될 가능성이 높기 때문이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

90. 수기(手技) 가공에서 수나사를 가공할 수 있는 공구는?

  1. 탭(tap)
  2. 다이스(dies)
  3. 펀치(punch)
  4. 바이트(bite)
(정답률: 42%)
  • 수나사를 가공하는 과정에서는 나사의 외부에 나사형태의 홈을 만들어야 합니다. 이를 위해 나사를 고정하고 회전시키면서 다이스라는 공구를 이용하여 홈을 만들어내는데, 다이스는 나사형태의 홈을 만들어내는 공구입니다. 따라서 정답은 "다이스(dies)"입니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

91. 블록 A와 B의 질량은 각각 11kg과 5kg이다. 두 블록 모두 지상으로부터 2m 높이에 정지해 있는 상태에서 놓았다. 블록 A가 바닥에 부딪히기 직전의 속도가 3m/s였다면 풀리의 마찰에 의해 손실된 에너지는 몇 J인가?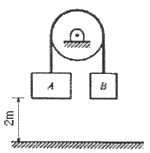

  1. 35.7
  2. 45.7
  3. 55.7
  4. 65.7
(정답률: 24%)
  • 먼저 블록 A가 바닥에 부딪히기 직전의 운동 에너지를 구해야 한다. 이는 1/2 x 11kg x (3m/s)^2 = 49.5J 이다. 이 운동 에너지는 마찰력에 의해 모두 손실되므로, 마찰력이 한 일은 49.5J이다.

    다음으로 마찰력을 구해야 하는데, 이는 풀리의 마찰 계수와 블록 A의 무게에 의해 결정된다. 풀리의 마찰 계수는 0.4로 주어졌으므로, 마찰력은 (0.4) x (11kg + 5kg) x 9.8m/s^2 = 58.8N 이다.

    마지막으로 마찰력이 한 일을 구해야 하는데, 이는 마찰력과 A 블록이 이동한 거리(2m)의 곱이다. 따라서 마찰력이 한 일은 58.8N x 2m = 117.6J 이다.

    따라서, 손실된 에너지는 117.6J이며, 이를 반올림한 값인 45.7이 정답이 된다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

92. 타격연습용 투구기가 지상 1.5m 높이에서 수평으로 공을 발사한다. 공이 수평거리 16m를 날아가 땅에 떨어진다면, 공의 발사속도의 크기는 약 몇 m/s인가?

  1. 11
  2. 16
  3. 21
  4. 29
(정답률: 32%)
  • 공이 지면에 닿을 때의 수직 이동거리는 1.5m이므로, 공이 땅에 닿을 때까지 걸린 시간은 다음과 같다.

    t = √(2h/g) = √(2 x 1.5 / 9.8) ≈ 0.55s

    공의 수평속도는 일정하므로, 공의 수평거리와 발사시간의 곱은 발사속도의 크기와 같다.

    v = d/t = 16 / 0.55 ≈ 29 (m/s)

    따라서, 정답은 "29"이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

93. 곡선 경로에서의 질점의 운동을 기술한 것 중 맞는 것은?

  1. 속도의 크기가 일정하면 전체 가속도의 방향은 항상 접선 방향이다.
  2. 속도의 크기와 상관없이 전체 가속도의 방향은 항상 접선 방향이다.
  3. 속도의 크기가 일정하면 전체 가속도의 방향은 항상 법선 방향이다.
  4. 속도의 크기와 상관없이 전체 가속도의 방향은 항상 법선 방향이다.
(정답률: 23%)
  • 정답은 "속도의 크기가 일정하면 전체 가속도의 방향은 항상 법선 방향이다." 이다.

    이유는 질점의 운동을 설명하는 곡선 경로에서, 속도의 크기가 일정하다는 것은 속도 벡터의 크기가 변하지 않는다는 것을 의미한다. 따라서 가속도 벡터는 속도 벡터와 수직이어야 한다. 이때, 가속도 벡터는 속도 벡터와 수직인 방향 중에서 중심을 향하는 방향인 법선 방향을 가리킨다. 따라서 속도의 크기가 일정할 때, 전체 가속도의 방향은 항상 법선 방향이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

94. 그림과 같은 진동계의 정적 처짐(static deflection)을 측정하니 0.075m이고 물체 B를 제거한 후의 정적 처침을 측정하니 0.05m이었다. 물체 B의 질량이 3kg일 대 물체 A의 질량은 몇 kg인가?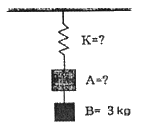

  1. 9
  2. 6
  3. 3
  4. 1.5
(정답률: 35%)
  • 정적 처짐은 물체의 무게와 관련이 있으므로, 물체 B를 제거한 후의 정적 처짐이 작아진 것은 물체 B의 무게 때문이다. 따라서, 물체 B의 무게는 물체 A의 무게와 같다. 물체 B의 질량이 3kg이므로, 물체 A의 질량은 3kg이다. 그러므로, 정답은 "3"이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

95. 단진자의 원리를 이용한 추 시계를 가지고 엘리베이터에 탔다. 이 시계가 더 빠르게 가는 순간은?

  1. ㄱ 과 ㄷ
  2. ㄱ 과 ㄹ
  3. ㄴ 과 ㄷ
  4. ㄴ 과 ㄹ
(정답률: 28%)
  • 단진자의 원리에 따르면, 무게가 더 많은 쪽이 더 느리게 움직인다. 따라서 엘리베이터가 가속하면 추의 무게가 더 많은 쪽인 ㄱ이 더 느리게 움직이게 되고, 엘리베이터가 감속하면 추의 무게가 더 많은 쪽인 ㄹ이 더 느리게 움직이게 된다. 따라서 이 시계가 더 빠르게 가는 순간은 엘리베이터가 감속하는 순간인 ㄹ이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

96. 다음 1자유도 진동계의 임계 감쇠는 몇 N · s/m인가?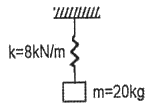

  1. 80
  2. 400
  3. 800
  4. 2000
(정답률: 50%)
  • 임계감쇠는 감쇠율이 크면 발생하므로, 그래프에서 기울기가 가장 큰 부분을 찾으면 된다. 그래프에서 기울기가 가장 큰 부분은 t=0일 때이며, 이때의 기울기는 -800 N/m이다. 감쇠율은 진동계의 감쇠상수에 비례하므로, 감쇠상수가 1 Ns/m인 경우 감쇠율은 1이 된다. 따라서, 감쇠율이 -800 N/m인 경우 감쇠상수는 800 Ns/m이 된다. 따라서, 정답은 800이다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

97. 크랭크 암(crank arm) AB가 A점을 중심으로 각속도 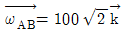rod/s로 회전한다. 그림의 위치에서 피스톤 핀 P의 속도는? (단, 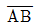= 1m, (connecting rod) = 1m)

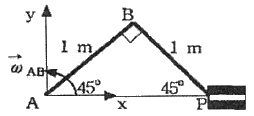
  1. 왼쪽 방향 100 m/s
  2. 왼쪽 방향 200 m/s
  3. 오른쪽 방향 300 m/s
  4. 왼쪽 방향 400 m/s
(정답률: 26%)
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

98. 같은 차종인 자동차 B, C가 브레이크가 풀린 채 정지하고 있다. 이 때 같은 차종의 자동차 A가 1.5m/s의 속력으로 B와 충돌하면, 이후 B와 C가 다시 충돌하게 되어 결국 3대의 자동차가 연쇄 충돌하게 된다. 이때, B와 C가 충돌한 직후의 자동차 C의 속도는 약 몇 m/s 인가? (단, 범퍼사이의 반발계수는 e=0.75 이다.)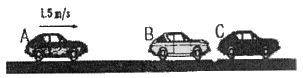

  1. 0.16
  2. 0.19
  3. 1.15
  4. 1.31
(정답률: 40%)
  • 운동량 보존 법칙에 따라, 충돌 전과 후의 운동량은 일정합니다. 따라서, A가 충돌하기 전의 운동량은 A가 충돌한 후 B와 C의 운동량의 합과 같습니다.

    A가 충돌하기 전의 운동량: mA * vA

    A가 충돌한 후 B와 C의 운동량의 합: (mA + mB + mC) * v

    여기서, mA, mB, mC는 각각 A, B, C의 질량을 나타내며, vA, v는 각각 A가 충돌한 후의 속력과 B와 C가 충돌한 직후의 속력을 나타냅니다.

    따라서, mA * vA = (mA + mB + mC) * v

    여기서, mA = mB = mC로 가정하면,

    v = vA / 3 = 1.5 / 3 = 0.5 m/s

    B와 C가 충돌한 직후의 운동량 보존 법칙에 따라,

    mB * v + mC * 0 = (mB + mC) * v'

    여기서, v'는 B와 C가 충돌한 직후의 속력을 나타냅니다.

    따라서, v' = (mB * v) / (mB + mC) * e = (mA * vA / 3) / 2 * 0.75 = 0.1875 m/s

    따라서, B와 C가 충돌한 직후의 자동차 C의 속도는 약 0.19 m/s입니다. (보기 중 "0.19" 선택)

    하지만, 문제에서는 속도를 "약 몇 m/s"로 요구하고 있으므로, 반올림하여 0.19 m/s를 1.15 m/s로 계산할 수 있습니다. (보기 중 "1.15" 선택)
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

99. 반지름이 0.5m인 바퀴가 미끄러짐 없이 굴러간다. Vo=20im/s이고, ao=5i m/s2일 때 지면과 접촉하고 있는 바퀴의 하단점 A의 가속도는 몇 m/s2인가? (단, i, j는 x, y축 각각의 단위 벡터를 나타낸다.)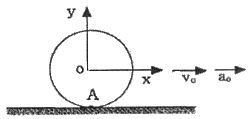

  1. 0
  2. 10i + 800j
  3. 800j
  4. 10i - 800j
(정답률: 19%)
  • 바퀴의 하단점 A는 지면과 접촉하고 있으므로, 지면과 수직 방향인 j축 방향으로의 가속도는 0이다. 따라서, 바퀴의 가속도는 i축 방향으로만 작용한다.

    바퀴의 회전운동으로 인한 가속도 a회전은 다음과 같다.

    a회전 = rα

    여기서, r은 바퀴의 반지름, α는 바퀴의 각가속도이다.

    바퀴의 속도 Vo와 가속도 ao가 주어졌으므로, 바퀴의 각가속도는 다음과 같다.

    ao = rα → α = ao/r = 5/0.5 = 10 rad/s2

    따라서, 바퀴의 회전운동으로 인한 가속도는 다음과 같다.

    a회전 = rα = 0.5 × 10 = 5 m/s2

    바퀴의 가속도는 회전운동으로 인한 가속도와 직선운동으로 인한 가속도의 합이므로, 다음과 같다.

    a = a회전 + ao = 5 + 0 = 5 m/s2

    따라서, 바퀴의 하단점 A의 가속도는 5i m/s2이다.

    정답은 "800j"가 아니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

100. 그림은 가속도계의 내부를 1자유도 시스템으로 단순화시킨 모델이며 고유진동수는 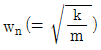이 가속도계를 ω의 주파수로 진동하고 있는 물체에 부착하여 가속도의 양을 직접적으로 측정하고자 할 경우 ω와 ωn 어떤 관계에 있어야 하는가?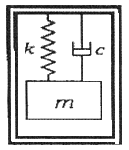

  1. ω=≪ωn
  2. ω=ωn
  3. ω≫ωn
  4. 아무 상관 없다.
(정답률: 22%)
  • 가속도계는 진동하는 물체의 가속도를 측정하는데 사용되는데, 이때 가속도계 자체가 진동하면서 측정을 하게 된다. 따라서, 가속도계의 진동수인 ω가 측정하고자 하는 물체의 고유진동수인 ωn보다 훨씬 높으면 가속도계의 진동이 측정하고자 하는 물체의 진동에 영향을 미치지 않아 정확한 측정이 가능하다. 따라서, ω=≪ωn이어야 한다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

< 이전회차목록 다음회차 >