1과목: 재료역학
1. 그림과 같은 막대가 있다. 길이는 4 m이고 힘은 지면에 평행하게 200 N 만큼 주었을 때 o점에 작용하는 힘과 모멘트는?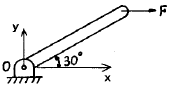
- Fox=0, Foy=200N, Mz=200Nㆍm
- Fox=200N, Foy=0, Mz=400Nㆍm
- Fox=200N, Foy=200N, Mz=200Nㆍm
- Fox=0, Foy=0, Mz=400Nㆍm
2. 두께 8 mm의 강판으로 만든 안지름 40 cm의 얇은 원통에 1 MPa의 내압이 작용할 때 강판에 발생하는 후프 응력(원주 응력)은 몇 MPa인가?
- 25
- 37.5
- 12.5
- 50
3. 그림과 같은 균일단면을 갖는 부정정보가 단순 지지단에서 모멘트 M0를 받는다. 단순지지단에서의 반력 Ra는? (단, 굽힘강성 EI는 일정하고, 자중은 무시한다.)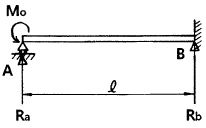
4. 진변형률(εT)과 진응력(σT)를 공칭 응력(σn)과 공칭 변형률(εn)로 나타낼 때 옳은 것은?
5. 폭 b=60 mm, 길이 L=340 mm의 균일강도 외팔보의 자유단에 집중하중 P=3 kN이 작용한다. 허용 굽힘응력을 65 MPa이라 하면 자유단에서 250 mm되는 지점의 두께 h는 약 몇 mm인가? (단, 보의 단면은 두께는 변하지만 일정한 폭 b를 갖는 직사각형이다.)
- 24
- 34
- 44
- 54
6. 부재의 양단이 자유롭게 회전할 수 있도록 되어있고, 길이가 4 m인 압축 부재의 좌굴 하중을 오일러 공식으로 구하면 약 몇 kN인가? (단, 세로탄성계수는 100 GPa이고, 단면 b × h=100 mm×50 mm이다.)
- 52.4
- 64.4
- 72.4
- 84.4
7. 평면 응력상태의 한 요소에 σx=100 MPa, σy=-50 MPa, τxy=0을 받는 평판에서 평면내에서 발생하는 최대 전단응력은 몇 MPa인가?
- 75
- 50
- 25
- 0
8. 탄성 계수(영계수) E, 전단 탄성 계수 G, 체적 탄성 계수 K사이에 성립되는 관계식은?
9. 바깥지름 50 cm, 안지름 30 cm의 속이 빈 축은 동일한 단면적을 가지며 같은 재질의 원형축에 비하여 약 몇 배의 비틀림 모멘트에 견딜 수 있는가? (단, 중공축과 중실축의 전단응력은 같다.)
- 1.1배
- 1.2배
- 1.4배
- 1.7배
10. 그림과 같은 단면에서 대칭축 n-n에 대한 단면 2차 모멘트는 약 몇 cm4인가?
- 535
- 635
- 735
- 835
11. 단면적이 2 cm2이고 길이가 4 m인 환봉에 10 kN의 축 방향 하중을 가하였다. 이때 환봉에 발생한 응력은 몇 N/m2인가?
- 5000
- 2500
- 5×105
- 5×107
12. 양단이 고정된 직경 30 mm, 길이가 10 m인 중실축에서 그림과 같이 비틀림 모멘트 1.5 kN ㆍ m가 작용할 때 모멘트 작용점에서의 비틀림 각은 약 몇 rad인가? (단, 봉재의 전단탄성계수 G=100 GPa이다.)(오류 신고가 접수된 문제입니다. 반드시 정답과 해설을 확인하시기 바랍니다.)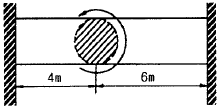
- 0.45
- 0.56
- 0.63
- 0.77
13. 그림과 같이 길이 ℓ인 단순 지지된 보 위를 하중 W가 이동하고 있다. 최대 굽힘응력은?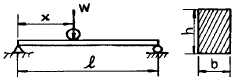
14. 그림과 같은 트러스가 점 B에서 그림과 같은 방향으로 5 kN의 힘을 받을 때 트러스에 저장되는 탄성에너지는 약 몇 kJ인가? (단, 트러스의 단면적은 1.2 cm2, 탄성계수는 106 Pa이다.)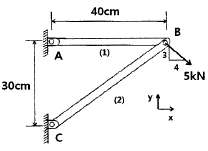
- 52.1
- 106.7
- 159.0
- 267.7
15. 길이 1 m인 외팔보가 아래 그림처럼 q=5 kN/m의 균일 분포하중과 P=1 kN의 집중 하중을 받고 있을 때 B점에서의 회전각은 얼마인가? (단, 보의 굽힘강성은 EI이다.)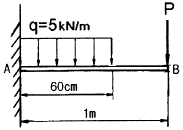
16. 그림과 같은 단순지지보에서 2 kN/m의 분포하중이 작용할 경우 중앙의 처짐이 0이 되도록 하기 위한 힘 P의 크기는 몇 kN인가?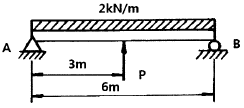
- 6.0
- 6.5
- 7.0
- 7.5
17. 그림과 같이 길이 ℓ=4 m의 단순보에 균일 분포하중 ω가 작용하고 있으며 보의 최대 굽힘응력 σmax=85 N/cm2일 때 최대 전단응력은 약 몇 kPa인가? (단, 보의 단면적은 지름이 11 cm인 원형단면이다.)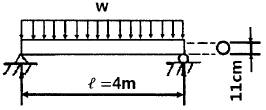
- 1.7
- 15.6
- 22.9
- 25.5
18. 그림과 같은 치차 전동 장치에서 A치차로부터 D치차로 동력을 전달한다. B와 C치 차의 피치원의 직경의 비가 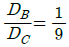 일 때, 두 축의 최대 전단응력들이 같아지게 되는 직경의 비
일 때, 두 축의 최대 전단응력들이 같아지게 되는 직경의 비 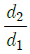 은 얼마인가?
은 얼마인가?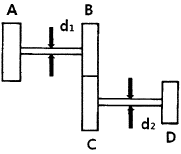
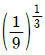
- 1/9
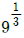
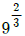
19. 그림과 같은 외팔보에 균일분포하중 ω가 전 길이에 걸쳐 작용할 때 자유단의 처짐 δ는 얼마인가? (단, E: 탄성계수, I: 단면2차모멘트이다.)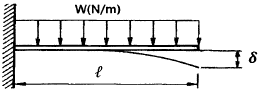
20. 그림과 같이 단면적이 2 cm2인 AB및 CD막대의 B점과 C점이 1 cm만큼 떨어져 있다. 두 막대에 인장력을 가하여 늘인 후 B점과 C점에 핀을 끼워 두 막대를 연결하려고 한다. 연결 후 두 막대에 작용하는 인장력은 약 몇 kN인가? (단, 재료의 세로탄성계수는 200 GPa이다.)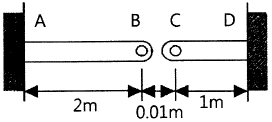
- 33.3
- 66.6
- 99.9
- 133.3
2과목: 기계열역학
21. 압력 2 MPa, 300 ℃의 공기 0.3 kg이 폴리트로픽 과정으로 팽창하여, 압력이 0.5 MPa로 변화하였다. 이때 공기가 한 일은 약 몇 kJ인가? (단, 공기는 기체상수가 0.287 kJ/(kg ㆍ K)인 이상기체이고, 폴리트로픽 지수는 1.3이다.)
- 416
- 157
- 573
- 45
22. 다음 중 기체상수(gas constant, R[kJ/(kg ㆍ K)] 값이 가장 큰 기체는?
- 산소(O2)
- 수소(H2)
- 일산화탄소(CO)
- 이산화탄소(CO2)
23. 이상기체 1 kg이 초기에 압력 2 kPa, 부피 0.1 m3를 차지하고 있다. 가역등온과정에 따라 부피가 0.3 m3로 변화했을 때 기체가 한 일은 약 몇 J인가?
- 9540
- 2200
- 954
- 220
24. 이상적인 오토사이클에서 열효율을 55 %로 하려면 압축비를 약 얼마로 하면 되겠는가? (단, 기체의 비열비는 1.4이다.)
- 5.9
- 6.8
- 7.4
- 8.5
25. 밀폐계가 가역정압 변화를 할 때 계가 받은 열량은?
- 계의 엔탈피 변화량과 같다.
- 계의 내부에너지 변화량과 같다.
- 계의 엔트로피 변화량과 같다.
- 계가 주위에 대해 한 일과 같다.
26. 유리창을 통해 실내에서 실외로 열전달이 일어난다. 이때 열전달량은 약 몇 W인가? (단, 대류열전달계수는 50 W/(m2 ㆍ K), 유리창 표면온도는 25 ℃, 외기온도는 10 ℃, 유리창면적은 2 m2이다.)
- 150
- 500
- 1500
- 5000
27. 어느 내연기관에서 피스톤의 흡기과정으로 실린더 속에 0.2 kg의 기체가 들어 왔다. 이것을 압축할 때 15 kJ의 일이 필요하였고, 10 kJ의 열을 방출하였다고 한다면, 이 기체 1 kg당 내부에너지의 증가량은?
- 10 kJ/kg
- 25 kJ/kg
- 35 kJ/kg
- 50 kJ/kg
28. 다음 중 강도성 상태량(intensive property)이 아닌 것은?
- 온도
- 압력
- 체적
- 밀도
29. 600 kPa, 300 K 상태의 이상기체 1 kmol이 엔탈피가 등온과정을 거쳐 압력이 200 kPa로 변했다. 이 과정동안의 엔트로피 변화량은 약 몇 kJ/K인가? (단, 일반기체상수 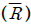 은 8.31451 kJ/(kmol ㆍ K)이다.)
은 8.31451 kJ/(kmol ㆍ K)이다.)
- 0.782
- 6.31
- 9.13
- 18.6
30. 그림과 같은 단열된 용기 안에 25 ℃의 물이 0.8 m3 들어있다. 이 용기 안에 100 ℃, 50 kg의 쇳덩어리를 넣은 후 열적 평형이 이루어졌을 때 최종 온도는 약 몇 ℃인가? (단, 물의 비열은 4.18 kJ/(kg ㆍ K), 철의 비열은 0.45 kJ/(kg ㆍ K)이다.)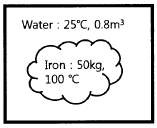
- 25.5
- 27.4
- 29.2
- 31.4
31. 실린더에 밀폐된 8 kg의 공기가 그림과 같이 P1=800 kPa, 체적 V1=0.27m3에서 P2=350 kPa, 체적 V2=0.80 m3으로 직선 변화하였다. 이 과정에서 공기가 한 일은 약 몇 kJ인가?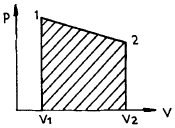
- 305
- 334
- 362
- 390
32. 어떤 기체 동력장치가 이상적인 브레이턴 사이클로 다음과 같이 작동할 때 이 사이클의 열효율은 약 몇 %인가? (단, 온도(T)-엔트로피(s) 선도에서 T1=30 ℃, T2=200 ℃, T3=1060 ℃, T4=160 ℃이다.)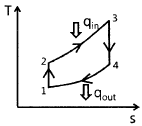
- 81 %
- 85 %
- 89 %
- 92 %
33. 이상기체에 대한 다음 관계식 중 잘못된 것은? (단, Cu는 정적비열, Cp는 정압비열, u는 내부에너지, T는 온도, V는 부피, h는 엔탈피, R은 기체상수, k는 비열비이다.)
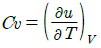
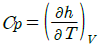
- Cp-Cu=R
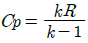
34. 열역학 제2법칙에 관해서는 여러 가지 표현으로 나타낼 수 있는데, 다음 중 열역학 제2법칙과 관계되는 설명으로 볼 수 없는 것은?
- 열을 일로 변환하는 것은 불가능하다.
- 열효율이 100 %인 열기관을 만들 수 없다.
- 열은 저온 물체로부터 고온 물체로 자연적으로 전달되지 않는다.
- 입력되는 일 없이 작용하는 냉동기를 만들 수 없다.
35. 계의 엔트로피 변화에 대한 열역학적 관계식 중 옳은 것은? (단, T는 온도, S는 엔트로피, U는 내부에너지, V는 체적, P는 압력, H는 엔탈피를 나타낸다.)
- Tds=dU-PdV
- Tds=dH-PdV
- Tds=dU-VdP
- Tds=dH-VdP
36. 공기 1 kg이 압력 50 kPa, 부피 3 m3인 상태에서 압력 900 kPa, 부피 0.5 m3인 상태로 변화할 때 내부 에너지가 160 kJ 증가하였다. 이 때 엔탈피는 약 몇 kJ이 증가하였는가?
- 30
- 185
- 235
- 460
37. 체적이 일정하고 단열된 용기 내에 80 ℃, 320 kPa의 헬륨 2 kg이 들어 있다. 용기 내에 있는 회전날개가 20 W의 동력으로 30분 동안 회전한다고 할 때 용기 내의 최종 온도는 약 몇 ℃인가? (단, 헬륨의 정적비열은 3.12 kJ/(kg ㆍ K)이다.)
- 81.9 ℃
- 83.3 ℃
- 84.9 ℃
- 85.8 ℃
38. 그림과 같은 Rankine 사이클로 작동하는 터빈에서 발생하는 일은 약 몇 kJ/kg인가? (단, h는 엔탈피, s는 엔트로피를 나타내며, h1=191.8 kJ/kg, h2=193.8 kJ/kg, h3=2799.5 kJ/kg, h4=2007.5 kJ/kg이다.)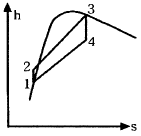
- 2.0 kJ/kg
- 792.0 kJ/kg
- 2605.7 kJ/kg
- 1815.7 kJ/kg
39. 시간당 380000 kg의 물을 공급하여 수증기를 생산하는 보일러가 있다. 이 보일러에 공급하는 물의 엔탈피는 830 kJ/kg이고, 생산되는 수증기의 엔탈피는 3230 kJ/kg이라고 할 때, 발열량이 32000 kJ/kg인 석탄을 시간당 34000 kg씩 보일러에 공급한다면 이 보일러의 효율은 약 몇 %인가?
- 66.9 %
- 71.5 %
- 77.3 %
- 83.8 %
40. 터빈, 압축기, 노즐과 같은 정상 유동장치의 해석에 유용한 몰리에(Molier) 선도를 옳게 설명한 것은?
- 가로축에 엔트로피, 세로축에 엔탈피를 나타내는 선도이다.
- 가로축에 엔트로피, 세로축에 온도를 나타내는 선도이다.
- 가로축에 엔트로피, 세로축에 밀도를 나타내는 선도이다.
- 가로축에 비체적, 세로축에 압력을 나타내는 선도이다.
3과목: 기계유체역학
41. 원관에서 난류로 흐르는 어떤 유체의 속도가 2배로 변하였을 때, 마찰계수가 변경 전 마찰계수의 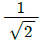 로 줄었다. 이때 압력손실은 몇 배로 변하는가?
로 줄었다. 이때 압력손실은 몇 배로 변하는가?
- √2배
- 2√2배
- 2배
- 4배
42. 점성계수가 0.3 N ㆍ s/m2이고, 비중이 0.9인 뉴턴유체가 지름 30 mm인 파이프를 통해 3 m/s의 속도로 흐를 때 Reynolds수는?
- 24.3
- 270
- 2700
- 26460
43. 어떤 액체의 밀도는 890 kg/m3, 체적 탄성계수는 2200 MPa이다. 이 액체 속에서 전파되는 소리의 속도는 약 몇 m/s인가?
- 1572
- 1483
- 981
- 345
44. 펌프로 물을 양수할 때 흡입측에서의 압력이 진공 압력계로 75 mmHg(부압)이다. 이 압력은 절대 압력으로 약 몇 kPa인가? (단, 수은의 비중은 13.6이고, 대기압은 760 mmHg이다.)
- 91.3
- 10.4
- 84.5
- 23.6
45. 동점성계수가 10 cm2/s이고 비중이 1.2인 유체의 점성계수는 몇 Pa ㆍ s인가?
- 0.12
- 0.24
- 1.2
- 2.4
46. 평판 위를 어떤 유체가 층류로 흐를 때, 선단으로부터 10 cm 지점에서 경계층두께가 1 mm일 때, 20 cm 지점에서의 경계층두께는 얼마인가?
- 1 mm
- √2 mm
- √3 mm
- 2 mm
47. 온도 27 ℃, 절대압력 380 kPa인 기체가 6 m/s로 지름 5 cm인 매끈한 원관 속을 흐르고 있을 때 유동상태는? (단, 기체상수는 187.8 N ㆍ m/(kg ㆍ K), 점성계수는 1.77×10-5 kg/(m ㆍ s), 상, 하 임계 레이놀즈수는 각각 4000, 2100이라 한다.)
- 층류영역
- 천이영역
- 난류영역
- 포텐셜영역
48. 2 m×2 m×2 m의 정육면체로 된 탱크 안에 비중이 0.8인 기름이 가득 차 있고, 위 뚜껑이 없을 때 탱크의 한 옆면에 작용하는 전체 압력에 의한 힘은 약 몇 kN인가?
- 7.6
- 15.7
- 31.4
- 62.8
49. 일정 간격의 두 평판 사이에 흐르는 완전 발달된 비압축성 정상유동에서 x는 유동방향, y는 평판 중심을 0으로 하여 x방향에 직교하는 방향의 좌표를 나타낼 때 압력강하와 마찰손실의 관계로 옳은 것은? (단, P는 압력, τ는 전단응력, μ는 점성계수(상수)이다.)
50. 비중 0.85인 기름의 자유표면으로부터 10 m 아래에서의 계기압력은 약 몇 kPa인가?
- 83
- 830
- 98
- 980
51. 물을 사용하는 원심 펌프의 설계점에서의 전양정이 30 m이고, 유량은 1.2 m3/min이다. 이 펌프를 설계점에서 운전할 때 필요한 축 동력이 7.35 kW라면 이 펌프의 효율은 약 얼마인가?
- 75 %
- 80 %
- 85 %
- 90 %
52. 그림과 같은 원형관에 비압축성 유체가 흐를 때 A단면의 평균속도가 V1일 때 B단면에서의 평균속도 V는?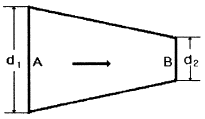
53. 유속 3 m/s로 흐르는 물 속에 흐름방향의 직각으로 피토관을 세웠을 때, 유속에 의해 올라가는 수주의 높이는 약 몇 m인가?
- 0.46
- 0.92
- 4.6
- 9.2
54. 2차원 유동장이  로 주어질 때, 가속도장
로 주어질 때, 가속도장 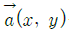 는 어떻게 표시되는가? (단, 유동장에서 c는 상수를 나타낸다.)
는 어떻게 표시되는가? (단, 유동장에서 c는 상수를 나타낸다.)
55. 그림과 같이 유속 10 m/s인 물 분류에 대하여 평판을 3 m/s의 속도로 접근하기 위하여 필요한 힘은 약 몇 N인가? (단, 분류의 단면적은 0.01 m2이다.)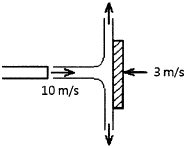
- 130
- 490
- 1350
- 1690
56. 물(비중량 9800 N/m3) 위를 3 m/s의 속도로 항진하는 길이 2 m인 모형선에 작용하는 조파저항이 54 N이다. 길이 50 m인 실선을 이것과 상사한 조파상태인 해상에서 항진시킬 때 조파 저항은 약 얼마인가? (단, 해수의 비중량은 10075 N/m3이다.)
- 43 kN
- 433 kN
- 87 kN
- 867 kN
57. 골프공 표면의 딤플(dimple, 표면 굴곡)이 항력에 미치는 영향에 대한 설명으로 잘못된 것은?
- 딤플은 경계층의 박리를 지연시킨다.
- 딤플이 층류경계층을 난류경계층으로 천이시키는 역할을 한다.
- 딤플이 골프공의 전체적인 항력을 감소시킨다.
- 딤플은 압력저항보다 점성저항을 줄이는데 효과적이다.
58. 다음과 같은 베르누이 방정식을 적용하기 위해 필요한 가정과 관계가 먼 것은? (단, 식에서 P는 압력, ρ는 밀도, V는 유속, γ는 비중량, Z는 유체의 높이를 나타낸다.)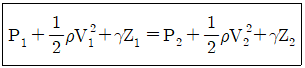
- 정상 유동
- 압축성 유체
- 비점성 유체
- 동일한 유선
59. 중력은 무시할 수 있으나 관성력과 점성력 및 표면장력이 중요한 역할을 하는 미세구조물 중 마이크로 채널 내부의 유동을 해석하는데 중요한 역할을 하는 무차원 수 만으로 짝지어진 것은?
- Reynolds 수, Froude 수
- Reynolds 수, Mach 수
- Reynolds 수, Weber 수
- Reynolds 수, Cauchy 수
60. 정상, 2차원, 비압축성 유동장의 속도성분이 아래와 같이 주어질 때 가장 간단한 유동함수(Ψ)의 형태는? (단, u는 x방향, υ는 y방향의 속도성분이다.)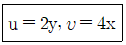
- Ψ=-2x2+Y2
- Ψ=-x2+y2
- Ψ=-x2+2y2
- Ψ=4x2+4y2
4과목: 기계재료 및 유압기기
61. S곡선에 영향을 주는 요소들을 설명한 것 중 틀린 것은?
- Ti, Al 등이 강재에 많이 함유될수록 S곡선은 좌측으로 이동된다.
- 강중에 첨가원소로 인하여 편석이 존재하면 S곡선의 위치도 변화한다.
- 강재가 오스테나이트 상태에서 가열온도가 상당히 높으면 높을수록 오스테나이트 결정립은 미세해지고, S곡선의 코(nose) 부근도 왼쪽으로 이동한다.
- 강이 오스테나이트 상태에서 외부로부터 응력을 받으면 응력이 커지게 되어 변태 시간이 짧아져 S곡선의 변태 개시선은 좌측으로 이동한다.
62. 구상흑연주철에서 나타나는 페딩(Fading) 현상이란?
- Ce, Mg첨가에 의해 구상 흑연화를 촉진하는 것
- 구상화처리 후 용탕상태로 방치하면 흑연구상화 효과가 소멸하는 것
- 코크스비를 낮추어 고온 용해하므로 용탕에 산소 및 황의 성분이 낮게 되는 것
- 두께가 두꺼운 주물이 흑연 구상화처리 후에도 냉각속도가 늦어 편상흑연조직으로 되는 것
63. 순철의 변태에 대한 설명 중 틀린 것은?
- 동소변태점은 A3점과 A4점이 있다.
- Fe의 자기변태점은 약 768 ℃ 정도이며, 퀴리(curie)점이라고도 한다.
- 동소변태는 결정격자가 변화하는 변태를 말한다.
- 자기변태는 일정온도에서 급격히 비연속으로 일어난다.
64. Fe-C 평형 상태도에서 γ고용체가 시멘타이트를 석출 개시하는 온도선은?
- Acm선
- A3선
- 공석선
- A2선
65. Mg-Al계 합금에 소량의 Zn과 Mn을 넣은 합금은?
- 엘렉트론(elektron) 합금
- 스텔라이트(stellite) 합금
- 알클래드(alclad) 합금
- 자마크(zamak) 합금
66. 경도시험에서 압입체의 다이아몬드 원추각이 120°이며, 기준하중이 10 kgf인 시험법은?
- 쇼어 경도시험
- 브리넬 경도시험
- 비커스 경도시험
- 로크웰 경도시험
67. 다음 금속 중 재결정 온도가 가장 높은 것은?
- Zn
- Sn
- Fe
- Pb
68. 아름답고 매끈한 플라스틱 제품을 생산하기 위한 금형재료의 요구되는 특성이 아닌것은?
- 결정입도가 클 것
- 편석 등이 적을 것
- 핀홀 및 흠이 없을 것
- 비금속 개재물이 적을 것
69. 심냉(sub-zero) 처리의 목적을 설명한 것 중 옳은 것은?
- 자경강에 인성을 부여하기 위한 방법이다.
- 급열ㆍ급냉 시 온도 이력현상을 관찰하기 위한 것이다.
- 항온 담금질하여 베이나이트 조직을 얻기 위한 방법이다.
- 담금질 후 변형을 방지하기 위해 잔류 오스테나이트를 마텐자이트 조직으로 얻기 위한 방법이다.
70. Al합금 중 개량처리를 통해 Si의 조대한 육각 판상을 미세화시킨 합금의 명칭은?
- 라우탈
- 실루민
- 문쯔메탈
- 두랄루민
71. 감압밸브, 체크밸브, 릴리프밸브 등에서 밸브시트를 두드려 비교적 높은 음을 내는 일종의 자려 진동 현상은?
- 유격 현상
- 채터링 현상
- 폐입 현상
- 캐비테이션 현상
72. 유압 파워유닛의 펌프에서 이상 소음 발생의 원인이 아닌 것은?
- 흡입관의 막힘
- 유압유에 공기 혼입
- 스트레이너가 너무 큼
- 펌프의 회전이 너무 빠름
73. 지름이 2 cm인 관속을 흐르는 물의 속도가 1 m/s이면 유량은 약 몇 cm3/s인가?
- 3.14
- 31.4
- 314
- 3140
74. 한 쪽 방향으로 흐름은 자유로우나 역방향의 흐름을 허용하지 않는 밸브는?
- 체크 밸브
- 셔틀 밸브
- 스로틀 밸브
- 릴리프 밸브
75. 다음 중 유량제어밸브에 의한 속도제어회로를 나타낸 것이 아닌 것은?
- 미터 인 회로
- 블리드 오프 회로
- 미터 아웃 회로
- 카운터 회로
76. 유체를 에너지원 등으로 사용하기 위하여 가압 상태로 저장하는 용기는?
- 디퓨져
- 액추에이터
- 스로틀
- 어큐뮬레이터
77. 점성계수(coefficient of viscosity)는 기름의 중요 성질이다. 점도가 너무 낮을 경우 유압기기에 나타나는 현상은?
- 유동저항이 지나치게 커진다.
- 마찰에 의한 동력손실이 증대된다.
- 각 부품 사이에서 누출 손실이 커진다.
- 밸브나 파이프를 통과할 때 압력손실이 커진다.
78. 저 압력을 어떤 정해진 높은 출력으로 증폭하는 회로의 명칭은?
- 부스터 회로
- 플립플롭 회로
- 온오프제어 회로
- 레지스터 회로
79. 베인펌프의 일반적인 구성 요소가 아닌 것은?
- 캠링
- 베인
- 로터
- 모터
80. 유공압 실린더의 미끄러짐 면의 운동이 간헐적으로 되는 현상은?
- 모노 피딩(Mono-feeding)
- 스틱 슬립(Stick-slip)
- 컷 인 다운(Cut in-down)
- 듀얼 액팅(Dual acting)
5과목: 기계제작법 및 기계동력학
81. 무게 20 N인 물체가 2개의 용수철에 의하여 그림과 같이 놓여 있다. 한 용수철은 1cm 늘어나는데 1.7 N이 필요하며 다른 용수철은 1 cm 늘어나는데 1.3 N이 필요하다. 변위 진폭이 1.25 cm가 되려면 정적 평형 위치에 있는 물체는 약 얼마의 초기속도(cm/s)를 주어야 하는가? (단, 이 물체는 수직 운동만 한다고 가정한다.)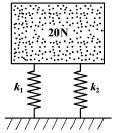
- 11.5
- 18.1
- 12.4
- 15.2
82. 전동기를 이용하여 무게 9800 N의 물체를 속도 0.3 m/s로 끌어올리려 한다. 장치의 기계적 효율을 80 %로 하면 최소 몇 kW의 동력이 필요한가?
- 3.2
- 3.7
- 4.9
- 6.2
83. 그림과 같이 Coulomb 감쇠를 일으키는 진동계에서 지면과의 마찰계수는 0.1, 질량 m= 100 kg, 스프링 상수 k=981 N/cm이다. 정지상태에서 초기 변위를 2 cm 주었다가 놓을 때 4 cycle후의 진폭은 약 몇 cm가 되겠는가?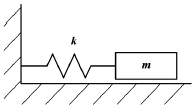
- 0.4
- 0.1
- 1.2
- 0.8
84. 단순조화운동(Harmonic motions)일 때 속도와 가속도의 위상차는 얼마인가?
- π/2
- π
- 2π
- 0
85. 어떤 물체가 정지 상태로부터 다음 그래프와 같은 가속도(a)로 속도가 변화한다. 이때 20초 경과 후의 속도는 약 몇 m/s인가?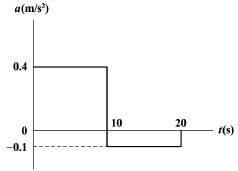
- 1
- 2
- 3
- 4
86. 그림은 스프링과 감쇠기로 지지된 기관(engine, 총 질량 m)이며, m1은 크랭크 기구의 불평형 회전 질량으로 회전 중심으로부터 r만큼 떨어져 있고, 회전주파수는 ω이다. 이 기관의 운동 방정식을 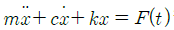 라고 할 때 F(t)로 옳은 것은?
라고 할 때 F(t)로 옳은 것은?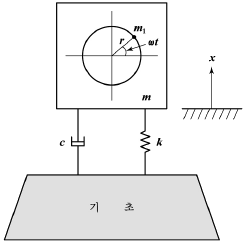
87. 반지름이 r인 균일한 원판의 중심에 200 N의 힘이 수평방향으로 가해진다. 원판의 미끄러짐을 방지하는데 필요한 최소 마찰력(F)은?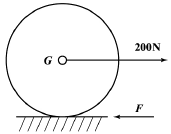
- 200 N
- 100 N
- 66.67 N
- 33.33 N
88. 축구공을 지면으로부터 1 m의 높이에서 자유낙하 시켰더니 0.8 m 높이까지 다시 튀어 올랐다. 이 공의 반발계수는 얼마인가?
- 0.89
- 0.83
- 0.80
- 0.77
89. 길이가 1 m이고 질량이 3 kg인 가느다란 막대에서 막대 중심축과 수직하면서 질량 중심을 지나는 축에 대한 질량 관성모멘트는 몇 kg ㆍ m2인가?
- 0.20
- 0.25
- 0.30
- 0.40
90. 아이스하키 선수가 친 퍽이 얼음 바닥 위에서 30 m를 가서 정지하였는데, 그 시간이 9초가 걸렸다. 퍽과 얼음 사이의 마찰계수는 얼마인가?
- 0.046
- 0.056
- 0.066
- 0.076
91. 다음 인발가공에서 인발 조건의 인자로 가장 거리가 먼 것은?
- 절곡력(folding force)
- 역장력(back tension)
- 마찰력(friction force)
- 다이각(die angle)
92. 다음 중 나사의 유효지름 측정과 가장 거리가 먼 것은?
- 나사 마이크로미터
- 센터게이지
- 공구현미경
- 삼침법
93. 구성인선(built up edge)의 방지 대책으로 틀린 것은?
- 공구 경사각을 크게 한다.
- 절삭 깊이를 작게 한다.
- 절삭 속도를 낮게 한다.
- 윤활성이 좋은 절삭유제를 사용한다.
94. 다음 중 전주가공의 특징으로 가장 거리가 먼 것은?
- 가공시간이 길다.
- 복잡한 형상, 중공축 등을 가공할 수 있다.
- 모형과의 오차를 줄일 수 있어 가공 정밀도가 높다.
- 모형 전체면에 균일한 두께로 전착이 쉽게 이루어진다.
95. 주조에서 탕구계의 구성요소가 아닌 것은?
- 쇳물받이
- 탕도
- 피이더
- 주입구
96. 다음 중 저온 뜨임의 특성으로 가장 거리가 먼 것은?
- 내마모성 저하
- 연마균열 방지
- 치수의 경년 변화 방지
- 담금질에 의한 응력 제거
97. TIG 용접과 MIG 용접에 해당하는 용접은?
- 불활성가스 아크 용접
- 서브머지드 아크 용접
- 교류 아크 셀룰로스계 피복 용접
- 직류 아크 일미나이트계 피복 용접
98. 다이(die)에 탄성이 뛰어난 고무를 적층으로 두고 가공 소재를 형상을 지닌 펀치로 가압하여 가공하는 성형가공법은?
- 전자력 성형법
- 폭발 성형법
- 엠보싱법
- 마폼법
99. 연강을 고속도강 바이트로 세이퍼 가공할 때 바이트의 1분간 왕복횟수는? (단, 절삭속도=15 m/min이고 공작물의 길이(행정의 길이)는 150 mm, 절삭행정의 시간과 바이트 1왕복의 시간과의 비 k=3/5이다.)
- 10회
- 15회
- 30회
- 60회
100. 드릴링 머신으로 할 수 있는 기본 작업 중 접시머리 볼트의 머리 부분이 묻히도록 원뿔자리 파기 작업을 하는 가공은?
- 태핑
- 카운터 싱킹
- 심공 드릴링
- 리밍






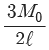
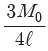

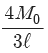
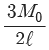 "이 정답이다.
"이 정답이다.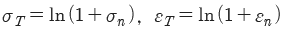
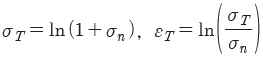
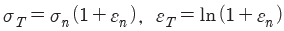
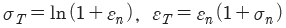
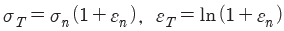 "이다.
"이다. 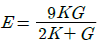

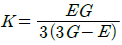
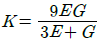
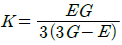 "이 정답인 이유는, 체적 탄성 계수 K를 구하는 식에서 탄성 계수 E와 v(포아송 비율)이 사용되기 때문입니다. 따라서 E와 v가 주어졌을 때 K를 구할 수 있으므로, K가 "
"이 정답인 이유는, 체적 탄성 계수 K를 구하는 식에서 탄성 계수 E와 v(포아송 비율)이 사용되기 때문입니다. 따라서 E와 v가 주어졌을 때 K를 구할 수 있으므로, K가 "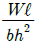
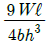
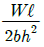
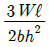
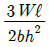 "이다.
"이다.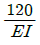
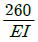
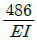
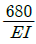
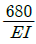 "이다.
"이다.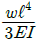
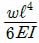
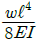
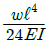
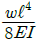 "은 δ가 L^4에 비례한다는 것을 나타내는 것이다. 다른 보기들은 δ와 관련이 없는 내용들이다.
"은 δ가 L^4에 비례한다는 것을 나타내는 것이다. 다른 보기들은 δ와 관련이 없는 내용들이다.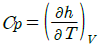 " 이다. 이유는 이 식에서 Cp와 Cv가 바뀌어 있기 때문이다. Cp는 정압비열이고 Cv는 정적비열이다. 따라서 올바른 식은 "
" 이다. 이유는 이 식에서 Cp와 Cv가 바뀌어 있기 때문이다. Cp는 정압비열이고 Cv는 정적비열이다. 따라서 올바른 식은 "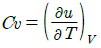 " 이다.
" 이다.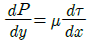
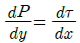
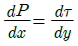
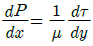
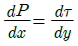 "이 맞는 이유이다. "
"이 맞는 이유이다. "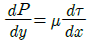 "은 압력강하와 마찰손실이 반비례 관계이므로 틀린 보기이고, "
"은 압력강하와 마찰손실이 반비례 관계이므로 틀린 보기이고, "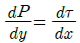 "와 "
"와 "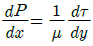 "는 압력강하와 마찰손실과는 직접적인 연관이 없는 보기이므로 틀린 보기이다.
"는 압력강하와 마찰손실과는 직접적인 연관이 없는 보기이므로 틀린 보기이다.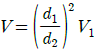
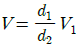
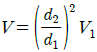
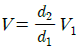
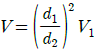 "입니다.
"입니다.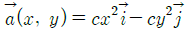
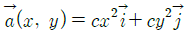

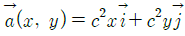
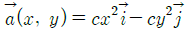 이므로, 이를 x와 y에 대해 각각 미분하면 가속도장은
이므로, 이를 x와 y에 대해 각각 미분하면 가속도장은 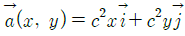 이 된다.
이 된다.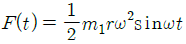
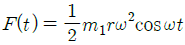
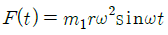
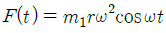
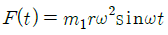 "이다.
"이다.