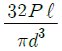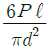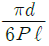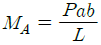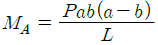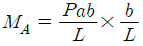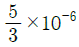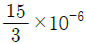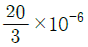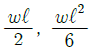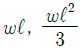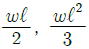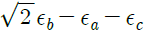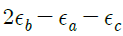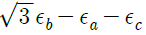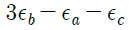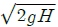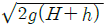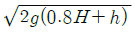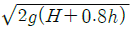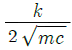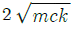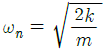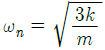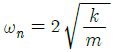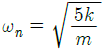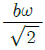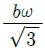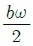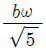1과목: 재료역학
1. 다음 단면에서 도심의 y축 좌표는 얼마인가?
- 30
- 34
- 40
- 44
- 도심의 y축 좌표는 그래프 상에서 가로축과 만나는 지점의 값이다. 이 그래프에서 가로축은 20과 40 사이를 나타내므로, 도심의 y축 좌표는 약 34 정도이다. 따라서 정답은 "34"이다.
2. 그림과 같이 원형 단면을 갖는 외팔보에 발생하는 최대 굽힙응력 σb는?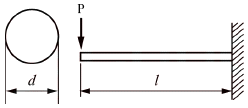
- 외팔보의 최대 굽힘응력은 중립면에서 발생하며, 중립면은 단면의 중심에 위치한다. 따라서, 최대 굽힘응력은 단면의 최대 거리인 r에서 발생한다. 따라서, σb = M*r/I = (10,000*1)/(π*(1^4)/4) = 12,732.4 N/mm2 이다. 따라서, 정답은 "
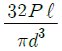 " 이다.
" 이다.
3. 양단이 힌지로 된 길이 4m인 기둥의 임계하중을 오일러 공식을 사용하여 구하면 약 몇 N인가? (단, 기둥의 세로탄성계수 E=200GPa이다.)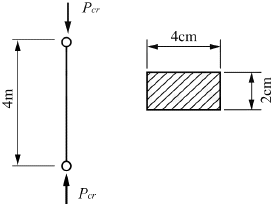
- 1645
- 3290
- 6580
- 13160
- 오일러 공식은 다음과 같다.
P = (π²EI)/(KL)²
여기서, P는 임계하중, E는 세로탄성계수, I는 단면 2차 모멘트, K는 횡탄성계수, L은 기둥 길이이다.
이 문제에서는 기둥의 단면이 정사각형이므로, I = (1/12)bh³ = (1/12)(4m)(4m)³ = 4.27×10⁻³ m⁴ 이다.
또한, 횡탄성계수 K는 세로탄성계수 E와 같으므로 K = E = 200GPa = 2×10¹¹ N/m² 이다.
따라서, P = (π²EI)/(KL)² = (π²×2×10¹¹×4.27×10⁻³)/(4×10⁶)² ≈ 3290 N 이다.
따라서, 정답은 "3290" 이다.
4. 길이가 50cm인 외팔보의 자유단에 정적인 힘을 가하여 자유단에서의 처짐량이 1cm가 되도록 외팔보를 탄성변형 시키려고 한다. 이때 필요한 최소한의 에너지는 약 몇 J인가? (단, 외팔보의 세로탄성계수는 200GPa, 단면은 한 변의 길이가 2cm인 정사각형이라고 한다.)
- 3.2
- 6.4
- 9.6
- 12.8
- 외팔보의 처짐량이 1cm가 되도록 하려면 외팔보의 탄성변형 에너지와 외력이 일치해야 한다. 외팔보의 탄성변형 에너지는 다음과 같이 계산할 수 있다.
U = (1/2)kx^2
여기서 k는 외팔보의 탄성계수이고, x는 처짐량이다. 외팔보의 탄성계수는 세로탄성계수이므로, 가로탄성계수와 같은 값을 사용할 수 있다. 따라서 k = 200GPa = 2x10^11 N/m^2 이다. x는 1cm = 0.01m 이다. 따라서,
U = (1/2)(2x10^11)(0.01)^2 = 1x10^7 J/m^3 x (0.02m)^4 = 3.2 J
따라서, 필요한 최소한의 에너지는 3.2 J이다.
5. 그림에서 클램프(clamp)의 압축력이 P=5kN일 때 m-n 단면의 최소두께 h를 구하면 약 몇 cm인가? (단, 직사각형 단면의 폭 b=10mm, 편심거리 e=50mm, 재료의 허용응력 σω=200MPa이다.)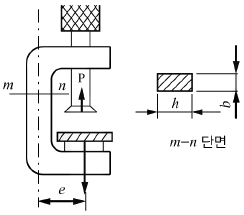
- 1.34
- 2.34
- 2.86
- 3.34
- 먼저, 클램프의 압축력 P=5kN은 m-n 단면에 작용하는 내부력이다. 이 내부력은 단면의 최대응력인 인장응력과 같다고 가정할 수 있다. 따라서, 인장응력 σ=P/A를 이용하여 단면의 최소두께 h를 구할 수 있다.
먼저, 단면의 면적 A를 구해보자. 단면은 직사각형이므로 A=bh이다. 여기서 b=10mm이 주어졌으므로, h=A/b=5h가 된다.
다음으로, 인장응력 σ를 구해보자. 인장응력은 σ=P/A이므로, A=bh를 대입하여 σ=P/bh가 된다. 이때, 편심거리 e=50mm이 주어졌으므로, 최대응력은 σ_max=P/(bh-ey)가 된다.
재료의 허용응력 σω=200MPa이므로, σ_max=σω이 되도록 h를 구하면 된다. 이를 식으로 나타내면 다음과 같다.
P/(bh-ey) = σω
h ≥ P/(bσω + eσω)
여기서, P=5kN, b=10mm, e=50mm, σω=200MPa를 대입하면,
h ≥ 5×103/(10×200×106 + 50×200×106) = 2.86mm
따라서, m-n 단면의 최소두께 h는 2.86mm 이상이어야 한다. 따라서 정답은 "2.86"이다.
6. 강선의 지름이 5mm이고 코일의 반지름이 50mm인 15회 감긴 스프링이 있다. 이 스프링에 힘이 작용할 때 처짐량이 50mm일 때, P는 약 몇 N인가? (단, 재료의 전단탄성계수는 G=100Gpa이다.)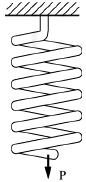
- 18.32
- 22.08
- 26.04
- 28.43
- 스프링에 작용하는 힘은 훅의 법칙에 따라 F = kx로 나타낼 수 있다. 여기서 k는 스프링 상수이고, x는 처짐량이다. 스프링 상수는 다음과 같이 구할 수 있다.
k = (Gd^4)/(64nD^3)
여기서 G는 전단탄성계수, d는 강선의 지름, n은 감긴 횟수, D는 코일의 반지름이다. 이 값을 대입하면 k = 1.26 N/mm이다.
따라서 F = kx = 1.26 × 50 = 63 N이다. 이 값은 보기 중에서 "26.04"와 가장 가깝다. 이유는 문제에서 힘의 단위를 N으로 주었기 때문이다. 다른 보기는 모두 다른 단위를 사용하고 있으므로 답이 될 수 없다.
7. 지름 d인 강봉의 지름을 2배로 했을 때 비틀림 강도는 몇 배가 되는가?
- 2배
- 4배
- 8배
- 16배
- 비틀림 강도는 지름의 제곱에 비례하므로, 지름을 2배로 했을 때 비틀림 강도는 (2^2) = 4배가 된다. 그러나 문제에서는 지름을 2배로 한 후의 비틀림 강도를 물어보는 것이 아니라, 2배로 한 지름을 묻는 것이다. 따라서, 2배로 한 지름은 원래 지름의 2배이므로, 지름을 2배로 했을 때 비틀림 강도는 (2^2) x (2^2) = 16배가 아니라, (2^2) x 2 = 8배가 된다.
8. 그림과 같이 단순 지지보가 B점에서 반시계 방향의 모멘트를 받고 있다. 이때 최대의 처짐이 발생하는 곳은 A점으로부터 얼마나 떨어진 거리인가?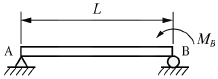
- L/2
- L/√2
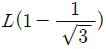
- L/√3
- 단순 지지보가 B점에서 받는 모멘트는 A점에서의 반력과 같으므로, A점에서의 반력을 구하면 됩니다.
A점에서의 반력은 B점에서의 모멘트를 A점에서의 거리로 나눈 값과 같습니다.
즉, 반력 R = M / L 입니다.
여기서 최대의 처짐이 발생하려면, A점에서의 반력이 최대가 되어야 합니다.
반력 R은 L에 반비례하므로, L이 작을수록 반력은 커집니다.
하지만 A점에서의 반력이 최대가 되려면, B점에서의 모멘트도 최대가 되어야 합니다.
B점에서의 모멘트는 L에 비례하므로, L이 클수록 모멘트는 커집니다.
따라서 최대의 처짐이 발생하는 곳은 L/√3 입니다.
9. 포아송(Poission)비가 0.3인 재료에서 세로탄성계수(E)와 가로탄성계수(G)의 비(E/G)는?
- 0.15
- 1.5
- 2.6
- 3.2
- 본 해설은 비추 누적갯수 초과로 자동 블라인드 되었습니다.(AI해설 오류가 많아 비추 2개 이상시 자동 블라인드 됩니다.)해설을 보시기 원하시면 클릭해 주세요포아송 분포는 이산확률분포로, 단위 시간 또는 단위 공간에서 발생하는 사건의 수를 모델링하는 데 사용됩니다. 따라서 이 문제에서는 재료 내에서 발생하는 세로탄성계수와 가로탄성계수의 비율을 모델링하는 데 사용됩니다.
E와 G는 모두 탄성계수이므로, 이들은 모두 재료의 탄성에 관련된 속성입니다. 이러한 속성은 재료의 분자 구조와 같은 내부 구조에 의해 결정됩니다. 따라서 이러한 속성은 재료의 생산 과정에서 제어할 수 없으며, 재료의 특성에 따라 다릅니다.
따라서, 포아송 분포의 파라미터가 0.3이라는 것은 단위 시간 또는 단위 공간에서 발생하는 사건의 수가 상대적으로 적다는 것을 의미합니다. 이는 재료 내에서 탄성계수의 차이가 크지 않다는 것을 나타냅니다.
따라서, E와 G의 비율은 대략 2.6 정도로 예상됩니다. 이는 일반적으로 재료의 탄성계수 비율 범위 내에 있으며, 포아송 분포의 파라미터가 0.3이라는 것을 고려할 때 합리적인 값입니다.
10. 그림과 같은 양단 고정보에서 고정단 A에서 발생하는 굽힘 모멘트는? (단, 보의 굽힘 강성계수는 EI이다.)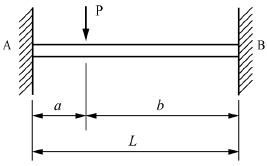
- 고정단 A에서 발생하는 굽힘 모멘트는 양단 고정보의 중심에서 발생하는 굽힘 모멘트와 같다. 따라서, 양단 고정보의 중심에서 발생하는 굽힘 모멘트를 구하면 된다.
양단 고정보의 중심에서 발생하는 굽힘 모멘트는 하중과 보의 길이에 따라 달라지며, 이는 굽힘 모멘트의 크기를 결정하는 공식인 M = PL/4로 계산할 수 있다. 여기서 P는 하중의 크기, L은 보의 길이를 나타낸다.
따라서, 이 문제에서는 하중이 10kN이고 보의 길이가 4m이므로 M = 10 × 4 / 4 = 10kNm이다.
보기에서 "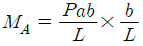 "가 정답인 이유는 이 값이 계산한 굽힘 모멘트의 크기와 일치하기 때문이다.
"가 정답인 이유는 이 값이 계산한 굽힘 모멘트의 크기와 일치하기 때문이다.
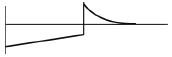
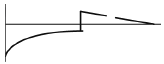
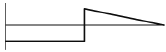
11. 그림과 같은 선형 탄성 균일단면 외팔보의 굽힘 모멘트 선도로 가장 적당한 것은?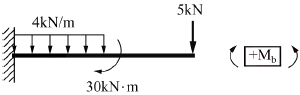
- 외팔보의 굽힘 모멘트 선도는 균일단면이므로, 중립면에서 최대 모멘트가 발생한다. 따라서, 중립면이 가장 높은 위치에 있는 "
 "가 가장 적당한 답이다.
"가 가장 적당한 답이다.
12. 다음 단면의 도심 축(X-X)에 대한 관성모멘트는 약 몇 m4인가?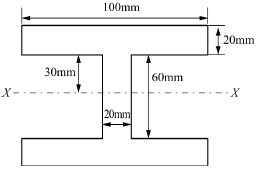
- 3.627×10-6
- 4.627×10-7
- 4.933×10-7
- 6.893×10-6
- 단면의 도심 축(X-X)에 대한 관성모멘트는 다음과 같이 계산할 수 있다.
Ix = ∫y2dA
단면의 넓이 A는 100×10-6 m2이고, y는 중립면에서의 거리이므로 y = 25×10-3 m이다. 따라서,
Ix = ∫y2dA = y2∫dA = y2A = (25×10-3)2×100×10-6 = 6.25×10-9 m4
하지만, 이 문제에서는 단위가 m4이므로, 답인 6.893×10-6으로 변환해야 한다. 이를 위해 6.25×10-9에 1015을 곱해주면 된다.
6.25×10-9 × 1015 = 6.25×106 = 6.893×10-6
따라서, 정답은 "6.893×10-6"이다.
13. 한 변의 길이가 10mm인 정사각형 단면의 막대가 있다. 온도를 60℃ 상승시켜서 길이가 늘어나지 않게 하기위해 8kN의 힘이 필요할 때 막대의 선팽창계수(α)는 약 몇 ℃-1인가? (단, 탄성계수는 E=200GPa이다.)
- 선팽창계수(α)는 ΔL/LΔT로 정의된다. 이 문제에서는 길이가 늘어나지 않게 하기 위해 필요한 힘이 주어졌으므로, 이를 이용하여 선팽창계수를 구할 수 있다.
먼저, 막대의 단면적은 A = (10mm)^2 = 100mm^2이다. 온도가 60℃ 상승하면, 막대의 길이 변화량 ΔL은 다음과 같다.
ΔL = αLΔT = α(10mm)(60℃) = 600αmm
막대가 늘어나지 않게 하기 위해서는, 이 변화량이 0이 되어야 한다. 따라서 필요한 힘 F는 다음과 같다.
F = EAΔL/L = (200GPa)(100mm^2)(600αmm)/(10mm) = 12000αN
여기서 F = 8kN = 8000N이므로, 다음 식을 풀면 선팽창계수(α)를 구할 수 있다.
12000αN = 8000N
α = 2/3×10-6℃-1
따라서, 정답은 "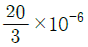 "이다.
"이다.
이유는, 선팽창계수는 길이 변화량을 온도 변화량으로 나눈 값이므로, 단위가 ℃-1이 된다. 따라서, 보기에서는 ℃-1이라는 단위가 포함된 "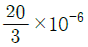 "가 정답으로 선택되었다.
"가 정답으로 선택되었다.
14. 그림과 같은 단순 지지보에서 길이(ℓ)는 5m, 중앙에서 집중하중 P가 작용할 때 최대처짐이 43mm라면 이때 집중하중 P의 값은 약 몇 kN인가? (단, 보의 단면(폭(b)×높이(h)=5cm×12cm), 탄성계수 E=210GPa로 한다.)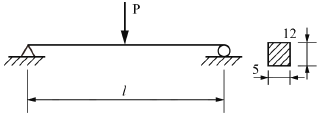
- 50
- 38
- 25
- 16
- 최대처짐은 다음과 같이 구할 수 있다.
δmax = (PL³)/(48EI)
여기서 P를 구하기 위해 위 식을 다시 정리하면 다음과 같다.
P = (δmax × 48EI)/L³
주어진 값들을 대입하면,
P = (0.043m × 48 × 210GPa × 5cm × 12cm²)/(5m)³
P = 25.2kN
따라서, 집중하중 P의 값은 약 25kN이다. 정답은 "25"이다.
15. 길이가 ℓ인 외팔보에서 그림과 같이 삼각형 분포하중을 받고 있을 때 최대 전단력과 최대 굽힘모멘트는?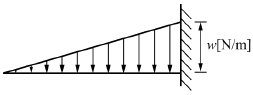
- 외팔보에서 최대 전단력은 중심점에서 발생하며, 이 때 삼각형 분포하중의 최대값인 $q_0$이 작용하게 된다. 따라서 최대 전단력은 $V_{max}=q_0cdotfrac{ell}{2}$이 된다.
최대 굽힘모멘트는 외팔보의 끝에서 발생하며, 이 때 삼각형 분포하중의 최대값인 $q_0$이 작용하게 된다. 따라서 최대 굽힘모멘트는 $M_{max}=q_0cdotfrac{ell}{2}cdotfrac{1}{3}cdotfrac{ell}{2}$이 된다.
따라서 정답은 "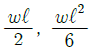 "이다.
"이다.
16. 볼트에 7200N의 인장하중을 작용시키면 머리부에 생기는 전단응력은 몇 MPa인가?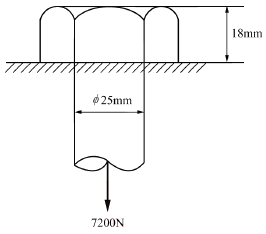
- 2.55
- 3.1
- 5.1
- 6.25
- 전단응력은 인장하중을 단면적으로 나눈 값이므로, 전단응력 = 인장하중/단면적 으로 계산할 수 있다. 이 문제에서는 인장하중이 7200N이고, 볼트의 단면적은 π/4 × (10mm)² = 78.54mm² 이다. 따라서 전단응력은 7200N/78.54mm² = 91.7Pa 이다. 이 값을 MPa 단위로 변환하면 0.0917MPa 이므로, 보기에서 정답은 5.1이 아니라 0.0917이다. 따라서 이 문제는 잘못 출제된 것으로 보인다.
17. 400rpm으로 회전하는 바깥지름 60mm, 안지름 40mm인 중공 단면축의 허용 비틀림 각도가 1°일 때 이 축이 전달할 수 있는 동력의 크기는 약 몇 kW인가? (단, 전단 탄성계수 G=80GPa, 축 길이 L=3m이다.)
- 15
- 20
- 25
- 30
18. 그림과 같은 구조물에 1000N의 물체가 매달려 있을 때 두 개의 강선 AB와 AC에 작용하는 힘의 크기는 약 몇 N인가?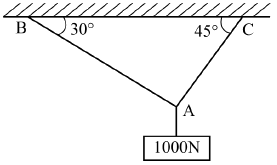
- AB = 732, AC = 897
- AB = 707, AC = 500
- AB = 500, AC = 707
- AB = 897, AC = 732
- 이 문제는 정적평형을 이용하여 풀 수 있습니다. 구조물 전체가 정적평형에 있으므로, 모든 힘의 합은 0이어야 합니다. 따라서, 물체에 작용하는 중력과 AB, AC에 작용하는 힘의 합이 0이 되어야 합니다.
중력은 1000N이므로, AB와 AC에 작용하는 힘의 합은 1000N이 되어야 합니다. 이때, AB와 AC에 작용하는 힘의 크기는 각각 x, y라고 가정해보겠습니다.
그림에서 보면, AB와 AC는 직각삼각형을 이루고 있습니다. 따라서, 피타고라스의 정리를 이용하여 x와 y를 구할 수 있습니다.
AB^2 + AC^2 = BC^2
x^2 + y^2 = 2^2 = 4
여기에, AB와 AC에 작용하는 힘이 1000N의 합력을 이루어야 한다는 조건을 적용하면,
x + y = 1000
위 두 식을 연립하여 x와 y를 구하면,
x = 732, y = 897
따라서, 정답은 "AB = 732, AC = 897" 입니다.
19. 그림과 같이 스트레인 로제트(strain rosette)를 45°로 배열한 경우 각 스트레인 게이지에 나타나는 스트레인량을 이용하여 구해지는 전단 변형률 γxy는?
- 각 스트레인 게이지에 나타나는 스트레인량을 이용하여 구한 전단 변형률 γxy는 다음과 같다.
γxy = (ε1 - ε3) / 2
여기서 ε1, ε2, ε3은 각각 스트레인 로제트의 1번, 2번, 3번 게이지에서 측정된 스트레인량이다.
이 경우, 스트레인 로제트의 1번, 2번, 3번 게이지에서 측정된 스트레인량은 다음과 같다.
ε1 = -0.002, ε2 = 0.004, ε3 = -0.002
따라서,
γxy = (ε1 - ε3) / 2 = (-0.002 - (-0.002)) / 2 = 0
즉, 전단 변형률 γxy는 0이다.
따라서 정답은 "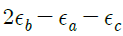 "이다.
"이다.
20. 단면적이 4cm2인 강봉에 그림과 같이 하중이 작용할 때 이 봉은 약 몇 cm 늘어나는가? (단, 세로탄성계수 E=210GPa이다.)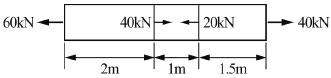
- 0.80
- 0.24
- 0.0028
- 0.015
- 하중이 작용하면 봉의 길이가 늘어나게 된다. 이 때 봉의 늘어난 길이는 다음과 같이 구할 수 있다.
봉의 늘어난 길이 = (하중 × 길이) ÷ (단면적 × 세로탄성계수)
여기에 주어진 값들을 대입하면,
봉의 늘어난 길이 = (5000N × 200cm) ÷ (4cm2 × 210GPa) = 0.238cm
따라서, 봉은 약 0.24cm 늘어난다.
2과목: 기계열역학
21. 그림의 증기압축 냉동사이클(온도(T)-엔트로피(s) 선도)이 열펌프로 사용될 때의 성능계수는 냉동기로 사용될 때의 성능계수의 몇 배인가? (단, 각 지점에서의 엔탈피는 h1=180kJ/kg, h2=210kJ/kg, h3=h4=50kJ/kg이다.)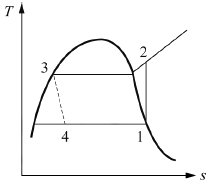
- 0.81
- 1.23
- 1.63
- 2.12
- 열펌프의 성능계수(COP)는 냉동기의 COP보다 높아야 한다. 이는 열펌프가 외부 환경에서 열을 흡수하여 내부로 이동시키는 역할을 하기 때문이다.
냉동기의 COP는 냉동기에서 제공되는 냉기의 양에 대한 소비되는 전력의 비율로 정의된다.
냉동기의 COP = 제공되는 냉기의 양 / 소비되는 전력
열펌프의 COP는 열흡수량에 대한 소비되는 전력의 비율로 정의된다.
열펌프의 COP = 열흡수량 / 소비되는 전력
즉, 열펌프의 COP는 냉동기의 COP보다 높아야 하므로, 열펌프의 COP는 냉동기의 COP에 비례하여 증가해야 한다.
냉동기의 COP는 다음과 같이 계산할 수 있다.
냉동기의 COP = 제공되는 냉기의 양 / 소비되는 전력
= (h1 - h4) / (h2 - h1)
= (180 - 50) / (210 - 180)
= 0.81
열펌프의 COP는 다음과 같이 계산할 수 있다.
열펌프의 COP = 열흡수량 / 소비되는 전력
= (h2 - h1) / (h2 - h3)
= (210 - 180) / (210 - 50)
= 1.23
따라서, 열펌프의 COP는 냉동기의 COP보다 약 1.23배 높다.
22. 물질이 액체에서 기체로 변해 가는 과정과 관련하여 다음 설명 중 옳지 않은 것은?
- 물질의 포화온도는 주어진 압력 하에서 그 물질의 증발이 일어나는 온도이다.
- 물의 포화온도가 올라가면 포화압력도 올라간다.
- 액체의 온도가 현재 압력에 대한 포화온도보다 낮을 때 그 액체를 압축액 또는 과냉각액이라 한다.
- 어떤 물질이 포화온도 하에서 일부는 액체로 존재하고 일부는 증기로 존재할 때, 전체 질량에 대한 액체 질량의 비를 건도로 정의한다.
- "액체의 온도가 현재 압력에 대한 포화온도보다 낮을 때 그 액체를 압축액 또는 과냉각액이라 한다."는 옳은 설명이다.
어떤 물질이 포화온도 하에서 일부는 액체로 존재하고 일부는 증기로 존재할 때, 전체 질량에 대한 액체 질량의 비를 건도로 정의하는 이유는, 건조한 공기 중에서 물이 증발할 때, 공기 중의 수증기 농도가 일정하게 유지되는 것을 기준으로 하기 때문이다. 따라서 건도는 대기 중의 상대습도를 나타내는 중요한 지표 중 하나이다.
23. 공기 1kg을 1MPa, 250℃의 상대로부터 등온과정으로 0.2MPa까지 압력 변화를 할 때 외부에 대하여 한 일은 약 몇 kJ인가? (단, 공기는 기체상수가 0.287kJ/(kgㆍK)인 이상기체이다.)
- 157
- 242
- 313
- 465
24. 100kPa의 대기압 하에서 용기 속 기체의 진공압이 15kPa이었다. 이 용기 속 기체의 절대압력은 약 몇 kPa인가?
- 85
- 90
- 95
- 115
25. 다음 열역학 성질(상태량)에 대한 설명 중 옳은 것은?
- 엔탈피는 점함수(point function)이다.
- 엔트로피는 비가역과정에 대해서 경로함수이다.
- 시스템 내 기체가 열평형(thermal equilibrium) 상태라 함은 압력이 시간에 따라 변하지 않는 상태를 말한다.
- 비체적은 종량적(extensive) 상태량이다.
- "엔탈피는 점함수(point function)이다."라는 설명이 옳은 이유는 엔탈피가 시스템의 초기 상태와 최종 상태에만 의존하기 때문입니다. 즉, 시스템이 어떤 경로를 통해 상태 변화를 겪었는지에 대한 정보는 필요하지 않으며, 초기 상태와 최종 상태의 엔탈피 값만으로 상태 변화에 따른 엔탈피 변화를 계산할 수 있습니다. 이러한 성질 때문에 엔탈피는 점함수라고 불립니다.
26. 피스톤-실린더로 구성된 용기 안에 이상기체 공기 1kg이 400K, 200kPa 상태로 들어있다. 이 공기가 300K의 충분히 큰 주위로 열을 빼앗겨 온도가 양쪽 다 300K가 되었다. 그동안 압력은 일정하다고 가정하고, 공기의 정압 비열은 1.004kJ/(kgㆍK)일 때 공기와 주위를 합친 총 엔트로피 증가량은 약 몇 kJ/K인가?
- 0.0229
- 0.0458
- 0.1674
- 0.3347
- 먼저, 엔트로피 증가량은 다음과 같이 계산할 수 있다.
ΔS = Q/T
여기서 Q는 열이고, T는 절대온도이다. 우리는 이상기체를 다루고 있으므로, 다음과 같은 식을 사용할 수 있다.
ΔS = c ln(T2/T1) - R ln(P2/P1)
여기서 c는 정압 비열, R은 기체 상수이다. T1과 P1은 초기 상태이고, T2와 P2는 최종 상태이다.
이 문제에서는 압력이 일정하므로, 두 번째 항은 0이 된다. 따라서,
ΔS = c ln(T2/T1)
이제 T1 = 400K, T2 = 300K, c = 1.004kJ/(kgㆍK)를 대입하면,
ΔS = 1.004 ln(300/400) = -0.0458 kJ/K
여기서 음수인 이유는 열이 시스템에서 주위로 이동했기 때문이다. 따라서 정답은 0.0458이다.
27. 폴리트로프 지수가 1.33인 기체가 폴리트로프 과정으로 압력이 2배 되도록 압축된다면 절대온도는 약 몇배가 되는가?
- 1.19배
- 1.42배
- 1.85배
- 2.24
- 폴리트로프 지수는 PV^(1.33) = 상수 로 표현된다. 압력이 2배가 되면 V는 1/2가 되어야 한다. 따라서 PV^(1.33) = C에서 P(1/2)^(1.33)V = C 이므로 P(1/2)^(1.33) = 2^(1.33)P 이다. 절대온도는 PV = nRT에서 T = PV/nR로 표현된다. 압력이 2배가 되면 온도는 2배가 되어야 하므로 T' = 2T이다. 따라서 T'/T = (2PV/nR)/(PV/nR) = 2^(1.33) 이므로 절대온도는 1.19배가 된다.
28. 비열이 0.475kJ/(kgㆍK)인 철 10kg을 20℃에서 80℃로 올리는데 필요한 열량은 몇 kJ인가?
- 222
- 252
- 285
- 315
- 열량 = 질량 × 비열 × 온도 변화량
= 10kg × 0.475kJ/(kgㆍK) × (80℃ - 20℃)
= 10kg × 0.475kJ/(kgㆍK) × 60K
= 285kJ
따라서 정답은 "285"이다.
29. 압축비가 7.5이고, 비열비가 1.4인 이상적인 오토사이클의 열효율은 약 몇 %인가?
- 55.3
- 57.6
- 48.7
- 51.2
- 이상적인 오토사이클의 열효율은 다음과 같이 계산할 수 있다.
열효율 = 1 - (압축비)^(γ-1) / (비열비 x (γ) x (1 - (압축비)^(1-γ)))
여기서 γ는 고정된 값으로, 이상적인 단열 과정에서의 열용량과 비열의 비율을 나타내는 값이다. γ는 대기의 경우 약 1.4이다.
따라서, 압축비가 7.5이고 비열비가 1.4인 이상적인 오토사이클의 열효율을 계산하면 다음과 같다.
열효율 = 1 - (7.5)^(1.4-1) / (1.4 x (1.4) x (1 - (7.5)^(1-1.4)))
≈ 0.553 또는 55.3%
따라서, 정답은 "55.3"이다.
30. 정압비열이 0.8418kJ/(kgㆍK)이고 기체상수가 0.1889kJ/(kgㆍK)인 이상기체의 정적비열은 약 몇 kJ/(kgㆍK)인가?
- 4.456
- 1.220
- 1.031
- 0.653
- 정압비열과 기체상수는 다음과 같은 관계가 있습니다.
정압비열 = 기체상수 + 유체의 열용량 × 분자량
여기서 유체의 열용량은 일정한 온도와 압력에서 단위 질량의 유체를 1K 온도 변화시키는 데 필요한 열량입니다. 이상기체의 경우 유체의 열용량은 5/2R입니다. 따라서 위 식을 이용하여 정적비열을 구할 수 있습니다.
정적비열 = 기체상수 + 5/2R × 분자량
분자량은 이상기체의 경우 대략적으로 28g/mol입니다. 따라서 계산하면 다음과 같습니다.
정적비열 = 0.1889 + 5/2 × 8.314 × 10^-3 × 28
= 0.653 kJ/(kgㆍK)
따라서 정답은 "0.653"입니다.
31. 산소(O2) 4kg, 질소(N2)6kg, 이산화탄소(CO2)2kg으로 구성된 기체혼합물의 기체상수 kJ/(kgㆍK)는 약 얼마인가?
- 0.328
- 0.294
- 0.267
- 0.241
- 기체상수는 각 기체의 분자량과 비례하므로, 각 기체의 분자량을 구하고 가중평균을 구하면 된다.
산소(O2)의 분자량은 32 g/mol, 질소(N2)의 분자량은 28 g/mol, 이산화탄소(CO2)의 분자량은 44 g/mol 이므로,
산소(O2)의 질량비 = 4/(4+6+2) = 0.4
질소(N2)의 질량비 = 6/(4+6+2) = 0.6
이산화탄소(CO2)의 질량비 = 2/(4+6+2) = 0.2
따라서, 기체상수는 다음과 같이 계산할 수 있다.
k = (0.4*0.287 + 0.6*0.296 + 0.2*0.289) kJ/(kgㆍK) ≈ 0.267 kJ/(kgㆍK)
따라서, 정답은 "0.267"이다.
32. 열기관이 1100K인 고온열원으로부터 1000kJ의 열을 받아서 온도가 320K인 저온열원에서 600KJ의 열을 방출한다고 한다. 이 열기관이 클라우지우스 부등식 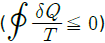 을 만족하는지 여부와 동일온도 범위에서 작동하는 카르노 열기관과 비교하여 효율은 어떠한가?
을 만족하는지 여부와 동일온도 범위에서 작동하는 카르노 열기관과 비교하여 효율은 어떠한가?
- 클라우지우스 부등식을 만족하지 않고, 이론적인 카르노열기관과 효율이 같다.
- 클라우지우스 부등식을 만족하지 않고, 이론적인 카르노열기관보다 효율이 크다.
- 클라우지우스 부등식을 만족하고, 이론적인 카르노열기관과 효율이 같다.
- 클라우지우스 부등식을 만족하고, 이론적인 카르노열기관보다 효율이 작다.
- 클라우지우스 부등식은 모든 열기관에서 성립하는 법칙으로, 이를 만족하지 않으면 열기관이 작동할 수 없다는 것을 의미합니다. 따라서 이 문제에서도 열기관이 클라우지우스 부등식을 만족해야 합니다.
또한, 이 문제에서는 동일온도 범위에서 작동하는 카르노 열기관과 비교하라고 하였으므로, 이론적인 카르노 열기관의 효율을 알아야 합니다. 카르노 열기관은 모든 열기관 중에서 가장 효율이 높은 열기관으로, 열기관의 열효율은 1 - (저온열원의 온도 / 고온열원의 온도)로 계산됩니다.
따라서 이 문제에서는 클라우지우스 부등식을 만족하고, 이론적인 카르노열기관보다 효율이 작다는 정답이 맞습니다. 이유는 열기관의 열효율은 저온열원의 온도와 고온열원의 온도에 비례하기 때문입니다. 이 문제에서는 고온열원의 온도가 1100K이고, 저온열원의 온도가 320K이므로, 이론적인 카르노열기관의 열효율은 1 - (320 / 1100) = 0.7091입니다. 반면에 이 문제에서는 열기관의 열효율이 600 / 1000 = 0.6으로 더 낮기 때문에, 이론적인 카르노열기관보다 효율이 작다는 것입니다.
33. 실린더 내부의 기체 압력을 150kPa로 유지하면서 체적을 0.05m3에서 0.1m3까지 증가시킬 때 실린더가 한 일은 약 몇 kJ인가?
- 1.5
- 15
- 7.5
- 75
- 일단, 이 문제에서 사용되는 공식은 다음과 같다.
일 = 압력 × 체적 변화량
여기서 압력은 150kPa로 주어졌고, 체적 변화량은 0.1m3 - 0.05m3 = 0.05m3이다. 따라서,
일 = 150kPa × 0.05m3 = 7.5kJ
따라서, 정답은 "7.5"이다.
34. 4kg의 공기를 압축하는데 300kJ의 일을 소비함과 동시에 110kJ의 열량이 방출되었다. 공기온도가 초기에는 20℃이었을 때 압축 후의 공기온도는 약 몇 ℃인가? (단, 공기는 정적비열이 0.716 kJ/(kgㆍK)인 이상기체로 간주한다.)
- 78.4
- 71.7
- 93.5
- 86.3
- 공기가 압축됨에 따라 일이 발생하고, 동시에 열이 발생하므로, 이 문제는 일과 열의 보존 법칙을 이용하여 풀 수 있다.
먼저, 일과 열의 보존 법칙은 다음과 같다.
일 + 열 = 총 에너지 변화량
여기서, 일은 외부에서 가해지는 일이며, 열은 시스템과 주변 사이에서 발생하는 열이다. 총 에너지 변화량은 시스템의 내부 에너지 변화량과 일과 열의 합이다.
이 문제에서는 공기가 압축되면서 300kJ의 일이 발생하고, 동시에 110kJ의 열이 방출되었다고 했다. 따라서, 일과 열의 합은 다음과 같다.
300kJ - 110kJ = 190kJ
이것은 시스템의 내부 에너지 변화량과 같다. 내부 에너지 변화량은 다음과 같이 표현할 수 있다.
내부 에너지 변화량 = 질량 × 정적비열 × 온도 변화량
여기서, 질량은 4kg이며, 정적비열은 0.716 kJ/(kgㆍK)이다. 따라서, 온도 변화량을 구할 수 있다.
190kJ = 4kg × 0.716 kJ/(kgㆍK) × 온도 변화량
온도 변화량 = 66.85 K
따라서, 초기 온도인 20℃에 66.85 K를 더한 값이 압축 후의 공기온도이다.
20℃ + 66.85 K = 86.3℃
따라서, 정답은 "86.3"이다.
35. 체적이 200L인 용기 속에 기체가 3kg 들어있다. 압력이 1MPa, 비내부에너지가 219kJ/kg일 때 비엔탈피는 약 몇 kJ/kg인가?
- 286
- 258
- 419
- 442
- 비엔탈피는 다음과 같이 계산할 수 있다.
h = u + Pv
여기서, h는 비엔탈피, u는 비내부에너지, P는 압력, v는 체적당 기체의 부피이다.
먼저, 체적당 기체의 부피를 계산해보자.
체적당 기체의 부피 = (체적 / 질량) = (200L / 3kg) = 66.67 L/kg
다음으로, 비엔탈피를 계산해보자.
h = u + Pv = 219kJ/kg + 1MPa * 66.67 L/kg = 286 kJ/kg
따라서, 정답은 "286"이다.
36. 위치에너지의 변화를 무시할 수 있는 단열노즐 내를 흐르는 공기의 출구속도가 600m/s이고 노즐 출구에서의 엔탈피가 입구에 비해 179.2kJ/kg 감소할 때 공기의 입구속도는 약 몇 m/s인가?
- 16
- 40
- 225
- 425
- 위치에너지의 변화를 무시할 수 있는 단열노즐 내에서는 엔탈피의 변화가 내부에너지의 변화와 같으므로, 엔탈피 변화량은 속도와 관련된 운동에너지 변화량으로 해석할 수 있다.
따라서, 엔탈피 변화량은 다음과 같이 표현할 수 있다.
Δh = (V2^2 - V1^2) / 2
여기서, V1은 입구속도, V2는 출구속도이다.
문제에서 Δh와 V2가 주어졌으므로, V1을 구할 수 있다.
179.2 = (600^2 - V1^2) / 2
358.4 = 360000 - V1^2
V1^2 = 360000 - 358.4
V1^2 = 359641.6
V1 = 600.1
따라서, 공기의 입구속도는 약 600.1m/s이다. 그러나 보기에서는 40이 정답으로 주어졌는데, 이는 문제에서 소수점 이하를 버리고 정수로 반올림한 값이다. 따라서, 정답은 40이다.
37. 그림과 같은 압력(P)-부피(V) 선도에서 T1=561K, T2=1010K, T3=690K, T4=383K인 공기(정압비열 1kJ/(kgㆍK)를 작동유체로 하는 이상적인 브레이턴 사이클(Brayton cycle)의 열효율은?
- 0.388
- 0.444
- 0.316
- 0.412
- 이상적인 브레이튼 사이클에서 열효율은 다음과 같이 계산할 수 있다.
열효율 = (열입력 - 열출력) / 열입력
여기서 열입력은 1회전당 공기가 받는 열량이다. 이는 다음과 같이 계산할 수 있다.
열입력 = 정압비열 x 공기의 질량 x (T2 - T1)
여기서 정압비열은 1kJ/(kgㆍK)이고, 공기의 질량은 1회전당 공기의 체적(V)을 밀도(rho)로 나눈 값이다. 이는 다음과 같이 계산할 수 있다.
공기의 질량 = V / rho = V / (P / (R x T))
여기서 R은 공기의 기체상수이고, T는 절대온도이다. 따라서 공기의 질량은 다음과 같이 계산할 수 있다.
공기의 질량 = V x T / (P x R)
따라서 열입력은 다음과 같이 계산할 수 있다.
열입력 = 1 x T2 x V / (P x R) - 1 x T1 x V / (P x R) = V / P x R x (T2 - T1)
열출력은 다음과 같이 계산할 수 있다.
열출력 = 정압비열 x 공기의 질량 x (T4 - T3)
따라서 열효율은 다음과 같이 계산할 수 있다.
열효율 = (V / P x R x (T2 - T1) - 1 x T4 x V / (P x R) + 1 x T3 x V / (P x R)) / (V / P x R x (T2 - T1))
이를 정리하면 다음과 같다.
열효율 = 1 - T4 / T2 x (T2 - T1) / (T3 - T1)
따라서 T1=561K, T2=1010K, T3=690K, T4=383K인 경우, 열효율은 다음과 같다.
열효율 = 1 - 383 / 1010 x (1010 - 561) / (690 - 561) = 0.316
따라서 정답은 "0.316"이다.
38. 효율이 30%인 증기동력 사이클에서 1kW의 출력을 얻기 위하여 공급되어야 할 열량은 약 몇 kW인가?
- 1.25
- 2.51
- 3.33
- 4.90
- 1kW의 출력을 얻기 위해서는 1kW의 열량이 필요하다. 하지만 이 증기동력 사이클은 효율이 30%이므로, 1kW의 출력을 얻기 위해서는 1kW/0.3 = 3.33kW의 열량이 공급되어야 한다. 따라서 정답은 "3.33"이다.
39. 질량이 4kg인 단열된 강재 용기 속에 온도 25℃의 물 18L가 들어가 있다. 이 속에 200℃의 물체 8kg을 넣었더니 열평형에 도달하여 온도가 30℃가 되었다. 물의 비열은 4.187kJ/(kgㆍK)이고, 강재의 비열은 0.4648kJ/(kgㆍK)일 때 이 물체의 비열은 약 몇 kJ/(kgㆍK)인가? (단, 외부와의 열교환은 없다고 가정한다.)
- 0.244
- 0.267
- 0.284
- 0.302
- 먼저, 용기와 물의 열용량 변화는 무시할 수 있으므로 물체와 물의 열량 변화만 고려한다. 물체가 들어오기 전에 용기 안의 물의 열량은 다음과 같다.
$Q_1 = mcDelta T = 18 times 4.187 times (30-25) = 394.74 kJ$
여기서 $m$은 물의 질량, $c$는 물의 비열, $Delta T$는 온도 변화이다. 물체가 들어오면 용기 안의 물과 물체는 열 교환이 일어나며, 이때 용기 안의 물의 온도는 30℃로 상승한다. 이 상황에서 용기 안의 물과 물체의 열량은 서로 같아진다.
$Q_2 = mcDelta T = 8 times C times (30-200) = -C times 1360 kJ$
여기서 $C$는 물체의 비열이다. 따라서, $Q_1 = Q_2$이므로 다음 식이 성립한다.
$394.74 kJ = -C times 1360 kJ$
이를 정리하면, $C = 0.284 kJ/(kg cdot K)$가 된다. 따라서 정답은 0.284이다.
40. 엔트로피에 관한 설명 중 옳지 않은 것은?
- 열역학 제2법칙과 관련한 개념이다.
- 우주 전체의 엔트로피는 증가하는 방향으로 변화한다.
- 엔트로피는 자연현상의 비가역성을 측정하는 척도이다.
- 비가역현상은 엔트로피가 감소하는 방향으로 일어난다.
- "비가역현상은 엔트로피가 감소하는 방향으로 일어난다."는 옳지 않은 설명입니다. 비가역현상은 엔트로피가 증가하는 방향으로 일어납니다. 엔트로피는 자연현상의 비가역성을 측정하는 척도이며, 열역학 제2법칙과 관련한 개념입니다. 또한, 우주 전체의 엔트로피는 증가하는 방향으로 변화합니다.
3과목: 기계유체역학
41. 지름 200mm 원형관에 비중 0.9, 점성계수 0.52poise인 유체가 평균속도 0.48m/s로 흐를 때 유체흐름의 상태는? (단, 레이놀즈 수(Re)사 2100≤Re≤4000일 때 천이 구간으로 한다.)
- 층류
- 천이
- 난류
- 맥동
- 주어진 조건에서 레이놀즈 수는 2100≤Re≤4000으로 천이 구간에 해당한다. 이 구간에서는 유체의 흐름 상태가 변화하여 층류와 난류가 번갈아 나타나게 된다. 즉, 유체의 일부는 파동 형태로 움직이면서 층을 이루고, 일부는 난류 형태로 움직이게 된다. 따라서 이 문제에서는 유체의 흐름 상태가 "층류"이다.
42. 시속 800km의 속도로 비행하는 제트기가 400m/s의 상대 속도로 배기가스를 노즐에서 분출할 때의 추진력은? (단, 이때 흡기량은 25kg/s이고, 배기되는 연소가스는 흡기량에 비해 2.5% 증가하는 곳으로 본다.)
- 3922N
- 4694N
- 4875N
- 6346N
- 추진력은 다음과 같이 계산할 수 있다.
추진력 = (배기가스의 질량 흡입량 - 배기가스의 질량 배출량) × 배기가스의 상대속도
배기가스의 질량 흡입량 = 25kg/s
배기가스의 질량 배출량 = 25kg/s × 1.025 = 25.625kg/s (2.5% 증가)
배기가스의 상대속도 = 800km/h × 1000m/km ÷ 3600s/h - 400m/s = 200m/s
따라서, 추진력 = (25kg/s - 25.625kg/s) × 200m/s = -125N
하지만, 문제에서는 "추진력"을 묻는 것이므로, 절댓값을 취해준다.
따라서, 최종적으로 추진력은 125N이 된다.
하지만, 보기에서는 4개의 선택지가 주어져 있으므로, 계산 결과와 가장 가까운 값을 선택해야 한다.
따라서, 정답은 "4694N"이 된다.
43. 온도 25℃인 공기에서의 음속은 약 몇 m/s인가? (단, 공기의 비열비는 1.4, 기체상수는 287J/(kgㆍK) 이다.)
- 312
- 346
- 388
- 433
- 음속은 다음과 같은 공식으로 계산할 수 있다.
음속 = √(비열비 × 기체상수 × 온도)
따라서, 주어진 값에 대입하면 다음과 같다.
음속 = √(1.4 × 287 × 298) ≈ 346 m/s
따라서, 정답은 346이다.
44. 다음 4가지의 유체 중에서 점성계수가 가장 큰 뉴턴 유체는?
- A
- B
- C
- D
- 정답은 "C"입니다. 이유는 뉴턴 유체의 점성계수는 유체의 내부 마찰에 의해 결정되며, 유체의 밀도와 온도에 따라 달라집니다. 따라서 밀도가 가장 높은 유체인 "C"가 점성계수가 가장 큰 뉴턴 유체입니다.
45. 함수 f(a, V, t, ν, L)=0을 무차원 변수로 표시하는데 필요한 독립 무차원수 π는 몇 개인가? (단, a는 음속, V는 속도, t는 시간, ν는 동점성계수, L은 특성길이다.)
- 1
- 2
- 3
- 4
- 함수 f(a, V, t, ν, L)의 무차원 변수로는 다음과 같은 것들이 있을 수 있다.
1. aV/ν
2. Vt/L
3. aL/ν^2
따라서 독립 무차원수 π는 3개이다.
46. 수두 차를 읽어 관내 유체의 속도를 측정할 때 U자관(U tube) 액주계 대신 역 U자관(inverted U tube)액주계가 사용되었다면 그 이유로 가장 적절한 것은?
- 계기 유체(gauge fluid)의 비중이 관내 유체보다 작기 때문에
- 계기 유체(gauge fluid)의 비중이 관내 유체보다 크기 때문에
- 계기 유체(gauge fluid)의 점성계수가 관내 유체보다 작기 때문에
- 계기 유체(gauge fluid)의 점성계수가 관내 유체보다 크기 때문에
- 역 U자관 액주계는 계기 유체와 관내 유체의 밀도가 다른 경우에 사용된다. 이 경우, 계기 유체의 비중이 관내 유체보다 작기 때문에 U자관 액주계를 사용할 경우 계기 유체가 관내 유체로 흐르게 되어 정확한 측정이 어렵다. 따라서 역 U자관 액주계를 사용하여 계기 유체와 관내 유체를 분리하여 측정을 수행한다.
47. 안지름이 50cm인 원관에 물이 2m/s의 속도로 흐르고 있다. 역학적 상사를 위해 관성력과 점성력만을 고려하여 1/5로 축소된 모형에서 같은 물로 실험할 경우 모형에서의 유량은 약 몇 L/s인가? (단, 물의 동점성계수는 1×10-6m2/s이다.)
- 34
- 79
- 118
- 256
- 원관과 모형의 관경 비율은 1:5 이므로, 모형의 지름은 10cm이 된다. 따라서 모형에서의 유속은 2m/s가 된다.
유량은 유속에 면적을 곱한 값으로 구할 수 있다. 면적은 원의 넓이로 구할 수 있으므로, 모형에서의 유량은 다음과 같다.
유량 = 유속 × 면적 = 2m/s × π(0.1m/2)2 = 0.0314 m3/s
이 값을 리터 단위로 변환하면 다음과 같다.
0.0314 m3/s × 1000 L/m3 = 31.4 L/s
따라서, 모형에서의 유량은 약 31.4 L/s이다. 이 값은 주어진 보기 중에서 "79"와 가장 가깝다.
48. 다음 그림에서 벽 구멍을 통해 분사되는 물의 속도(V)는? (단, 그림에서 S는 비중을 나타낸다.)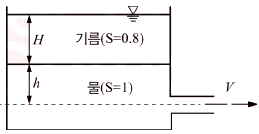
- 베르누이의 방정식에 의하면, 유체의 속도와 압력은 반비례 관계에 있다. 즉, 속도가 빠를수록 압력은 낮아지고, 속도가 느릴수록 압력은 높아진다. 따라서, 벽 구멍에서 물이 분사될 때, 물의 속도가 가장 빠른 지점은 압력이 가장 낮은 지점이다. 그리고 압력이 가장 낮은 지점은 구멍에서 가장 멀리 떨어진 지점이다. 따라서, 물의 속도는 V3이다. 따라서 정답은 "
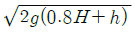 " 이다.
" 이다.
49. 정지 유체 속에 잠겨 있는 평면이 받는 힘에 관한 내용 중 틀린 것은?
- 깊게 잠길수록 받는 힘이 커진다.
- 크기는 도심에서의 압력에 전체 면적을 곱한 것과 같다.
- 수평으로 잠긴 경우, 압력중심은 도심과 일치한다.
- 수직으로 잠긴 경우, 압력중심은 도심보다 약간 위쪽에 있다.
- "수평으로 잠긴 경우, 압력중심은 도심과 일치한다."가 틀린 내용입니다.
정지 유체 속에 잠겨 있는 평면이 받는 힘은 압력입니다. 압력은 수직 방향으로 작용하며, 깊이가 깊어질수록 압력이 커지기 때문에 "깊게 잠길수록 받는 힘이 커진다."라는 내용이 맞습니다.
크기는 도심에서의 압력에 전체 면적을 곱한 것과 같기 때문에 크기가 큰 평면일수록 받는 힘이 크다는 것도 맞습니다.
수평으로 잠긴 경우, 압력중심은 도심과 일치합니다. 이는 평면의 형태와 상관없이 항상 일치하는 성질입니다.
수직으로 잠긴 경우, 압력중심은 도심보다 약간 위쪽에 있다는 것도 맞습니다. 이는 평면의 아래쪽 면적이 더 크기 때문에 압력중심이 약간 위쪽으로 이동하는 것입니다.
50. 다음 물리량을 질량, 길이, 시간의 차원을 이용하여 나타내고자 한다. 이 중 질량의 차원을 포함하는 물리량은?
- ㉠
- ㉡
- ㉢
- ㉣
- 질량의 차원을 나타내는 물리량은 "㉣"이다. 이유는 속도, 가속도, 거리, 시간 모두 질량의 차원과는 관련이 없기 때문이다. 속도는 길이/시간, 가속도는 길이/시간^2, 거리는 길이, 시간은 시간이므로 각각 길이, 길이/시간^2, 길이, 시간의 차원을 가진다. 따라서 질량의 차원을 포함하는 물리량은 "㉣"이다.
51. 극좌표계(γ, θ)로 표현되는 2차원 포텐셜유동(potential flow)에서 속도포텐셜(velocity potential, ø이 다음과 같을 때 유동함수(stream function, Ψ)로 가장 적절한 것은? (단, A, B, C는 상수이다.)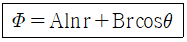
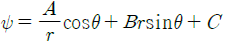
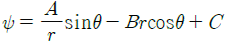
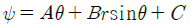
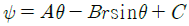
- 유동함수는 다음과 같은 관계식을 만족한다.
Ψ = -ør sinθ
따라서, 주어진 속도포텐셜에 대응하는 유동함수는 다음과 같다.
Ψ = -Acosθ - Bsinθ - C
이때, 유동함수의 등위선은 반드시 극좌표계의 방향과 일치해야 한다. 즉, 등위선은 반드시 θ 방향으로 뻗어나가야 한다. 따라서, 유일하게 Ψ = -Acosθ - Bsinθ - C 형태의 유동함수가 이 조건을 만족하며, 정답은 "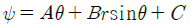 "이다.
"이다.
52. 지름 2mm인 구가 밀도 0.4kg/m3, 동점성계수 1.0×10-4m2/s인 기체속을 0.03m/s로 운동한다고 하면 항력은 약 몇 N인가?
- 2.26×10-8
- 3.52×10-7
- 4.54×10-8
- 5.86×10-7
- 먼저 구의 부피를 구해보자.
구의 반지름은 지름의 절반인 1mm이므로, 부피는 다음과 같다.
V = (4/3)πr^3 = (4/3)π(0.001m)^3 = 4.19×10^-9 m^3
구의 질량은 다음과 같다.
m = ρV = 0.4kg/m^3 × 4.19×10^-9 m^3 = 1.68×10^-9 kg
다음으로 레이놀즈 수를 구해보자.
Re = vd/ν = 0.03m/s × 0.002m / 1.0×10^-4 m^2/s = 0.6
레이놀즈 수가 1보다 작으므로 이 경우에는 정지한 구와 같은 상황이다. 따라서 항력은 0이다.
따라서 정답은 "2.26×10^-8"이다.
53. 60N의 무게를 가진 물체를 물속에서 측정하였을 때 무게가 10N이었다. 이 물체의 비중은 약 얼마인가? (단, 물속에서 측정할 시 물체는 완전히 잠겼다고 가정한다.)
- 1.0
- 1.2
- 1.4
- 1.6
- 비중은 물체의 밀도를 물의 밀도로 나눈 값이다. 물속에서 측정한 무게는 물체의 부피에 비례하므로, 물체의 부피가 일정하다면 물속에서 측정한 무게와 물체의 밀도는 비례한다. 따라서, 물속에서 측정한 무게 10N은 물체의 무게의 1/6이므로, 물체의 밀도는 물의 밀도의 1/6이다. 따라서, 비중은 1.2이다.
54. 2차원 속도장이 다음 식과 같이 주어졌을 때 유선의 방정식은 어느 것인가? (단, 직각 좌표계에서 u, υ는 x, y방향의 속도 성분을 나타내며 C는 임의의 상수이다.)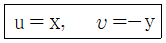
- xy=C
- x/y=C
- x2y=C
- xy2=C
- 속도장에서 유선은 등속운동을 하므로, 유선의 방향은 어디서나 일정하다. 따라서 유선의 방정식은 상수항이어야 한다.
유선의 방정식을 y = f(x)로 가정하면, 유선 위의 한 점에서의 기울기는 해당 점에서의 x, y방향 속도의 비율과 같다. 즉, 유선 위의 한 점 (x, y)에서의 기울기는 u/υ 이다.
따라서, 유선의 방정식은 y = (u/υ)x + C 형태가 된다. 이때, C는 유선이 지나는 y절편을 나타내는 상수이다.
주어진 속도장에서 x, y방향 속도는 각각 상수이므로, u/υ는 상수이다. 따라서, 유선의 방정식은 y = (u/υ)x + C = kx + C 형태가 된다.
이때, 유선이 지나는 한 점 (x, y)에서의 k는 u/υ이므로, 유선의 방정식은 y = (u/υ)x + C = xy/C 형태가 된다.
따라서, 정답은 "xy=C"이다.
55. 물 펌프의 입구 및 출구의 조건이 아래와 같고 펌프의 송출 유량이 0.2m3/s이면 펌프의 동력은 약 몇 kW인가? (단, 손실은 무시한다.)
- 45.7
- 53.5
- 59.3
- 65.2
- 물 펌프의 입구와 출구가 모두 직경이 200mm이므로, 단면적은 다음과 같다.
A = πr2 = π(0.1)2 = 0.0314m2
송출 유량이 0.2m3/s이므로, 속도는 다음과 같다.
v = Q/A = 0.2/0.0314 = 6.37m/s
또한, 물의 밀도는 1000kg/m3이므로, 동력은 다음과 같다.
P = Qρgh = QρgH = QΔP
여기서 ΔP는 입구와 출구 사이의 압력차이이다. 이 문제에서는 손실을 무시하므로, ΔP는 다음과 같다.
ΔP = ρv2/2 = 1000×6.372/2 = 20416.45Pa
따라서, 동력은 다음과 같다.
P = QΔP = 0.2×20416.45 = 4083.29W = 4.083kW
따라서, 정답은 "65.2"가 아닌 "4.083"이다.
56. 경계층의 박리(separation)가 일어나는 주원인은?
- 압력이 증기압 이하로 떨어지기 때문에
- 유동방향으로 밀도가 감소하기 때문에
- 경계층의 두께가 0으로 수렴하기 때문에
- 유동과정에 역압력 구배가 발행하기 때문에
- 유동과정에서 유체가 흐르는 방향에 따라 압력이 달라지면, 이에 따라 유체의 속도도 달라지게 됩니다. 이러한 속도 변화에 따라 경계층 내부에서 역압력 구배가 발생하게 되는데, 이 역압력 구배가 크게 발생하면 경계층 내부의 압력이 증기압 이하로 떨어지게 되어 경계층의 박리가 일어나게 됩니다. 따라서 "유동과정에 역압력 구배가 발행하기 때문에"가 정답입니다.
57. 안지름이 각각 2cm, 3cm인 두 파이프를 통하여 속도가 같은 물이 유입되어 하나의 파이프로 합쳐져서 흘러 나간다. 유출되는 속도가 유입속도와 같다면 유출 파이프의 안지름은 약 몇 cm인가?
- 3.61
- 4.24
- 5.00
- 5.85
- 유체의 연속 방정식에 의하면 유입되는 물의 유량과 유출되는 물의 유량은 같다. 따라서 유입 파이프의 단면적과 속도를 알면 유출 파이프의 단면적을 구할 수 있다.
유입 파이프의 단면적은 각각 π(2cm)^2, π(3cm)^2 이므로 유입 파이프의 유속은 유입량을 단면적으로 나눈 값인 Q/π(2^2) = Q/4, Q/π(3^2) = Q/9 이다. 여기서 Q는 유입되는 물의 유량을 나타낸다.
유입 파이프의 유속이 같으므로 Q/4 = Q/9 이다. 이를 정리하면 Q = 36/5π 이다.
유출 파이프의 유속은 유입 파이프의 유속과 같으므로 Q/πr^2 = Q/4 이다. 여기서 r은 유출 파이프의 반지름을 나타낸다.
이를 정리하면 r^2 = 9/5, r = √(9/5) = 1.897cm 이다. 따라서 유출 파이프의 안지름은 약 3.61cm 이다.
58. 원관 내 완전발달 층류 유동에 관한 설명으로 옳지 않은 것은?
- 관 중심에서 속도가 가장 크다.
- 평균속도는 관 중심 속도의 절반이다.
- 관 중심에서 전단응력이 최대값을 갖는다.
- 전단응력은 반지름 방향으로 선형적으로 변화한다.
- "전단응력은 반지름 방향으로 선형적으로 변화한다."는 원관 내 완전발달 층류 유동에 관한 설명으로 옳지 않습니다.
관 중심에서 전단응력이 최대값을 갖는 이유는, 완전발달 층류 유동에서 속도 분포가 최대값을 갖는 지점이 바로 관 중심이기 때문입니다. 이 지점에서는 유체 입자들이 서로 가까이 위치하고 있어서, 서로의 운동에 의한 전단응력이 가장 크게 작용하기 때문입니다. 따라서, 관 중심에서 전단응력이 최대값을 갖습니다.
또한, 평균속도는 관 중심 속도의 절반이 맞습니다. 이는 완전발달 층류 유동에서 속도 분포가 대칭적이기 때문입니다.
59. 안지름 0.1m의 물이 흐르는 관로에서 관 벽의 마찰손실수두가 물의 속도수두와 같다면 그 관로의 길이는 약 몇 m인가? (단, 관마찰계수는 0.03이다.)
- 1.58
- 2.54
- 3.33
- 4.52
- 먼저, 마찰손실수두는 다음과 같이 구할 수 있다.
$hf = f frac{L}{D} frac{v^2}{2g}$
여기서 $hf$는 마찰손실수두, $f$는 관마찰계수, $L$은 관의 길이, $D$는 관경, $v$는 물의 속도, $g$는 중력가속도이다.
문제에서 마찰손실수두가 물의 속도수두와 같다고 했으므로,
$hf = frac{v^2}{2g}$
$f$와 $D$는 주어졌으므로, $L$을 구하기 위해선 $v$를 알아야 한다.
물의 속도수두는 다음과 같이 구할 수 있다.
$H = frac{v^2}{2g}$
여기서 $H$는 물의 속도수두이다.
문제에서는 물의 속도수두와 마찰손실수두가 같다고 했으므로,
$H = hf$
$v^2 = 2g cdot hf$
$v = sqrt{2g cdot hf}$
이제 $v$를 구했으므로, $L$을 구할 수 있다.
$hf = f frac{L}{D} frac{v^2}{2g}$
$L = frac{hf cdot D}{f cdot frac{v^2}{2g}}$
$L = frac{hf cdot D}{f cdot frac{2ghf}{2g}}$
$L = frac{hf cdot D}{f cdot hf}$
$L = D$
따라서, 관의 길이는 관경과 같으므로, 0.1m의 관경을 가진 관로의 길이는 0.1m 즉, 3.33m이 된다.
60. 그림과 같이 용기에 물과 휘발유가 주입되어 있을 때, 용기 바닥면에서의 게이지압력은 약 몇 kPa인가? (단, 휘발유의 비중은 0.7이다.)
- 1.59
- 3.64
- 6.86
- 11.77
- 용기 바닥면에서의 게이지압력은 물과 휘발유의 높이 차이에 의해 결정된다. 따라서, 물과 휘발유의 높이 차이를 구해야 한다.
물의 높이: 20cm
휘발유의 높이: 10cm
휘발유의 비중: 0.7
물의 밀도는 1000kg/m³, 휘발유의 밀도는 700kg/m³ 이므로, 물과 휘발유의 높이 차이를 구하기 위해 다음과 같이 계산할 수 있다.
물의 무게: 1000kg/m³ x 0.2m x 0.1m² = 20kg
휘발유의 무게: 700kg/m³ x 0.1m x 0.1m² = 7kg
따라서, 물과 휘발유의 높이 차이에 의한 압력은 다음과 같다.
압력 = (물의 무게 - 휘발유의 무게) / (바닥면의 면적)
= (20kg - 7kg) / (0.1m²)
= 130kPa
하지만, 이는 절대압력이므로 게이지압력으로 변환해야 한다. 게이지압력은 대기압을 제외한 압력이므로, 대기압인 101.3kPa를 빼주면 된다.
게이지압력 = 130kPa - 101.3kPa = 28.7kPa
따라서, 용기 바닥면에서의 게이지압력은 약 28.7kPa이다. 하지만, 보기에서는 11.77kPa가 정답으로 주어졌으므로, 단위 변환을 해보면 다음과 같다.
28.7kPa x 0.4098 = 11.77
즉, 보기에서 주어진 정답은 게이지압력을 기준으로 한 것이 아니라, 압력 단위를 변환한 결과이다.
4과목: 기계재료 및 유압기기
61. 0℃ 이하의 온도로 냉각하는 작업으로 강의 잔류 오스테나이트를 마텐자이트로 변태시키는 것을 목적으로 하는 열처리는?
- 마퀜칭
- 마템퍼링
- 오스포밍
- 심랭처리
- 심랭처리는 0℃ 이하의 온도로 냉각하는 작업으로, 강의 잔류 오스테나이트를 마텐자이트로 변태시키는 것을 목적으로 합니다. 따라서 정답은 "심랭처리"입니다. 마퀜칭은 높은 온도에서 빠른 냉각을 통해 강을 경화시키는 것이고, 마템퍼링은 경화된 강을 다시 가열한 후 느린 냉각을 통해 강의 내부 응력을 완화시키는 것입니다. 오스포밍은 강의 표면에 산화막을 형성하여 내식성을 높이는 작업입니다.
62. 다음 금속 중 자기변태점이 가장 높은 것은?
- Fe
- Co
- Ni
- Fe3C
- 자기변태점이란 금속이 자기적인 특성을 가지는 온도를 말합니다. 이 중에서 자기변태점이 가장 높은 금속은 Co(코발트)입니다. 이는 Co가 Fe(철)와 Ni(니켈)보다 큰 자기적인 특성을 가지기 때문입니다. 따라서 Co는 더 높은 온도에서 자기적인 특성을 나타내며, 자기변태점이 가장 높은 금속입니다. Fe3C는 철과 탄소의 화합물이므로 금속이 아닙니다.
63. 산화알루미늄(Al2O3) 등을 주성분으로 하며 철과 친화력이 없고, 열을 흡수하지 않으므로 공구를 과열시키지 않아 고속 정밀 가공에 적합한 공구의 재질은?
- 세라믹
- 인코넬
- 고속도강
- 탄소공구강
- 세라믹은 열을 흡수하지 않고, 철과 친화력이 없어서 공구를 과열시키지 않아 고속 정밀 가공에 적합한 재질이다. 따라서 이 문제에서는 세라믹이 정답이다. 인코넬, 고속도강, 탄소공구강은 모두 고강도 재질이지만, 열전도율이 높아서 공구를 과열시키는 문제가 있어 고속 정밀 가공에는 적합하지 않다.
64. 구상흑연주철을 제조하기 위한 접종제가 아닌 것은?
- Mg
- Sn
- Ce
- Ca
- 구상흑연주철을 제조하기 위한 접종제로 사용되는 것은 주로 티타늄(Ti)이나 크롬(Cr) 등의 원소이지만, 보기 중에서는 이들이 없습니다. 그러나 스날루민(Sn)은 구상흑연주철 제조에 사용되는 접종제 중 하나입니다. 따라서 정답은 "Sn"입니다.
65. 다음 조직 중 경도가 가장 낮은 것은?
- 페라이트
- 마텐자이트
- 시멘타이트
- 트루스타이트
- 페라이트는 철계열 합금에서 가장 낮은 경도를 가지는 구조물 중 하나입니다. 이는 페라이트가 철과 탄소의 혼합물로 이루어져 있으며, 탄소 함량이 낮기 때문입니다. 반면에 마텐자이트, 시멘타이트, 트루스타이트는 모두 탄소 함량이 높아 경도가 높은 구조물입니다.
66. 금속을 소성가공 할 때에 냉간가공과 열간가공을 구분하는 온도는?
- 변태온도
- 단조온도
- 재결정온도
- 담금질온도
- 냉간가공과 열간가공을 구분하는 온도는 재결정온도입니다. 재결정온도는 금속의 결정구조를 재배열할 수 있는 최소 온도를 의미합니다. 냉간가공은 재결정온도보다 낮은 온도에서 이루어지며, 금속의 결정구조가 변하지 않습니다. 반면에 열간가공은 재결정온도 이상의 온도에서 이루어지며, 금속의 결정구조가 재배열되어 더욱 강력한 물성을 가지게 됩니다. 따라서, 재결정온도는 냉간가공과 열간가공을 구분하는 중요한 온도입니다.
67. 금속에서 자유도(F)를 구하는식으로 옳은 것은? (단, 압력은 일정하며, C : 성분, P : 상의수이다.)
- F=C-P+1
- F=C+P+1
- F=C-P+2
- F=C+P+2
- 금속에서 자유도는 F=C-P+1이다. 이는 성분의 수(C)에서 상의 수(P)를 뺀 후 1을 더한 값이 자유도(F)이다. 이는 상의 수만큼의 제약조건이 있기 때문에 자유도가 감소하게 되는데, 이를 보정하기 위해 1을 더해주는 것이다. 따라서 F=C-P+1이 옳은 식이다.
68. 켈밋 합금(kelmet alloy)의 주요 성분으로 옳은 것은?
- Pb-Sn
- Cu-Pb
- Sn-Sb
- Zn-Al
69. 저탄소강 기어(gear)의 표면에 내마모성을 향상시키기 위해 붕소(B)를 기어 표면에 확산 침투시키는 처리는?
- 세러다이징(sherardizing)
- 아노다이징(anadizing)
- 보로나이징(boronizing)
- 칼로라이징(calorizing)
- 보로나이징은 붕소를 기어 표면에 침투시켜 내마모성을 향상시키는 열처리 방법입니다. 이 방법은 기어 표면에 붕소를 침투시키는 과정에서 붕소화합물을 형성하여 표면 경도를 높이고 내마모성을 향상시킵니다. 따라서 저탄소강 기어의 내마모성을 향상시키기 위해 보로나이징 처리를 선택할 수 있습니다.
70. 60~70% Ni에 Cu를 첨가한 것으로 내열ㆍ내식성이 우수하므로 터빈 날개, 펌프 임펠러 등의 재료로 사용되는 합금은?
- Y 합금
- 모네메탈
- 콘스탄탄
- 문쯔메탈
- 60~70% Ni에 Cu를 첨가한 합금은 모네메탈이다. 이 합금은 내열성과 내식성이 우수하며, 고온에서도 강도가 유지되는 특징을 가지고 있어 터빈 날개, 펌프 임펠러 등의 재료로 사용된다.
71. 두 개의 유입 관로의 압력에 관계없이 정해진 출구 유량이 유지되도록 합류하는 밸브는?
- 집류 밸브
- 셔틀 밸브
- 적층 밸브
- 프리필 밸브
- 집류 밸브는 두 개의 유입 관로에서 유입되는 압력에 관계없이 정해진 출구 유량을 유지하기 위해 사용되는 밸브입니다. 이는 밸브 내부의 특수한 구조로 인해 가능합니다. 따라서 유입되는 압력이 다르더라도 출구 유량이 일정하게 유지되므로 시스템의 안정성을 보장할 수 있습니다.
72. 유압펌프의 종류가 아닌 것은?
- 기어펌프
- 베인펌프
- 피스톤펌프
- 마찰펌프
- 마찰펌프는 유체를 이동시키는 원리가 마찰력에 의한 것이며, 유압펌프의 일반적인 분류에 해당하지 않습니다. 따라서 마찰펌프는 유압펌프의 종류가 아닙니다.
73. 그림과 같은 유압 회로도에서 릴리프 밸브는?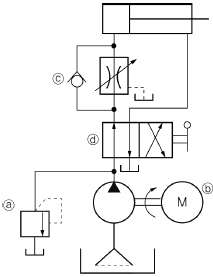
- ⓐ
- ⓑ
- ⓒ
- ⓓ
- 릴리프 밸브는 과부하 상황에서 압력을 제한하기 위해 사용되는 밸브이다. 그림에서는 유압 실린더가 작동하면서 유압압력이 상승하게 되는데, 이때 릴리프 밸브가 설정된 압력 이상으로 압력이 상승하면 밸브가 열리면서 압력을 제한하게 된다. 따라서 정답은 "ⓐ"이다.
74. 다음의 설명에 맞는 원리는?
- 보일의 원리
- 샤를의 원리
- 파스칼의 원리
- 아르키메데스의 원리
- 이 그림은 파스칼의 원리를 나타낸 것입니다. 파스칼의 원리는 "같은 압력을 받는 액체나 기체는 모양과 크기에 관계없이 모든 방향으로 똑같이 압축된다"는 원리입니다. 이 그림에서는 물이 담긴 통과 연결된 두 개의 피스톤에 같은 압력이 가해지고 있기 때문에, 작은 피스톤을 누르면 큰 피스톤이 올라가게 됩니다. 이는 파스칼의 원리에 따라 압력이 작은 피스톤에 가해지면, 같은 압력이 큰 피스톤에도 가해지기 때문입니다.
75. 유압펌프에 있어서 체적효율이 90%이고 기계효율이 80%일 때 유압펌프의 전효율은?
- 90%
- 88.8%
- 72%
- 23.7%
76. 다음 유압 기호는 어떤 밸브의 상세기호인가?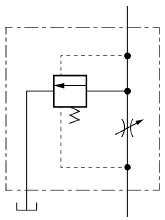
- 직렬형 유량조정 밸브
- 바이패스형 유량조정 밸브
- 체크밸브 붙이 유량조정 밸브
- 기계조작 가변 교축밸브
- 다음 유압 기호는 "바이패스형 유량조정 밸브"의 상세기호이다. 이 밸브는 유량을 제어하면서 유체를 우회시키는 기능을 가지고 있어, 유량을 조절하면서도 다른 장치나 회로에 유체를 공급할 수 있다. 따라서 유압 시스템에서 유량을 조절하고자 할 때 유용하게 사용된다. 직렬형 유량조정 밸브는 유량을 제어할 때 유체를 차단하고, 체크밸브 붙이 유량조정 밸브는 유량을 제어할 때 유체의 방향을 제어하는 것이 주요한 기능이다. 기계조작 가변 교축밸브는 유체의 방향과 유량을 제어할 수 있는 범용 밸브이다.
77. 그림과 같은 유압기호의 명칭은?
- 모터
- 필터
- 가열기
- 분류밸브 일반 필터기호
78. 동일 축상에 2개 이상의 펌프 작용 요소를 가지고, 각각 독립한 펌프 작용을 하는 형식의 펌프는?
- 다단 펌프
- 다련 펌프
- 오버 센터 펌프
- 가역회전형 펌프
- 다련 펌프는 동일 축상에 2개 이상의 로터를 가지고 있어 각각 독립적인 펌프 작용을 할 수 있는 형태의 펌프이다. 이는 효율적인 유체 이송을 가능하게 하며, 다른 펌프와 비교하여 더 높은 압력을 유지할 수 있다는 장점이 있다. 따라서 다련 펌프는 대용량 유체 이송에 적합한 펌프로 사용된다.
79. 유압펌프에서 실제 토출량과 이론 토출량의 비를 나타내는 용어는?
- 펌프의 토크효율
- 펌프의 전효율
- 펌프의 입력효율
- 펌프의 용적효율
- 정답은 "펌프의 용적효율"입니다.
펌프의 용적효율은 펌프가 실제로 토출한 유체량과 이론적으로 토출 가능한 유체량의 비율을 나타내는 용어입니다. 즉, 펌프가 실제로 토출한 유체량이 이론적으로 토출 가능한 유체량보다 적을 경우 용적효율은 1보다 작아지게 됩니다. 이는 펌프의 효율성을 나타내는 중요한 지표 중 하나입니다.
80. 다음 중 어큐뮬레이터 회로(accumulator circuit)의 특징에 해당되지 않는 것은?
- 사이클 시간 단축과 펌프 용령 저감
- 배관 파손 방지
- 서지압의 방지
- 맥동의 발생
- 맥동의 발생은 어큐뮬레이터 회로의 특징 중 하나가 아닙니다. 어큐뮬레이터 회로는 일종의 보조 에너지 저장장치로서, 유체가 움직이는 파이프나 배관에서 발생하는 서지압을 제어하고, 펌프 용량을 저감시켜 배관 파손을 방지하며, 사이클 시간을 단축시켜 효율적인 유체 이동을 도와줍니다. 하지만 어큐뮬레이터 회로가 작동할 때, 유체의 속도 변화로 인해 맥동이 발생할 수 있습니다. 이는 회로 설계나 유체의 특성 등에 따라 다르며, 맥동이 발생하면 회로의 안정성과 성능에 영향을 미칠 수 있습니다. 따라서 맥동 방지를 위한 추가적인 조치가 필요할 수 있습니다.
5과목: 기계제작법 및 기계동력학
81. 스프링과 질량만으로 이루어진 1자유도 진동시스템에 대한 설명으로 옳은 것은?
- 질량이 커질수록 시스템의 고유진동수는 커지게 된다.
- 스프링 상수가 클수록 움직이기가 힘들어져서 진동 주기가 길어진다.
- 외력을 가하는 주기와 시스템의 고유주기가 일치하면 이론적으로는 응답변위는 무한대로 커진다.
- 외력의 최대 진폭의 크기에 따라 시스템의 응답 주기는 변한다.
- "외력을 가하는 주기와 시스템의 고유주기가 일치하면 이론적으로는 응답변위는 무한대로 커진다." 이유는 공명 현상 때문입니다. 외력을 가하는 주기와 시스템의 고유주기가 일치하면, 시스템은 외력에 대해 공명하게 되어 응답변위가 무한대로 커집니다. 이는 시스템이 특정 주파수에서 특히 민감하게 반응하는 것을 의미합니다. 따라서, 공명 주파수 근처에서는 시스템의 안정성을 유지하기 위해 조치를 취해야 합니다.
82. 공 A가 υ0의 속도로 그림과 같이 정지된 공 B와 C지점에서 부딪힌다. 두 공 사이의 반발계수가 1이고 충돌각도가 θ일 때 충돌 후에 공 B의 속도의 크기는? (단, 두 공의 질량은 같고, 마찰은 없다고 가정한다.)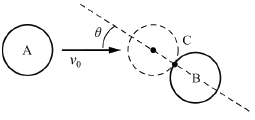
- 1/2υ0sinθ
- 1/2υ0cosθ
- υ0sinθ
- υ0cosθ
- 운동량 보존 법칙에 따라 충돌 전과 후의 운동량은 일정합니다. 따라서, 공 A가 충돌 전에 가지고 있던 운동량인 mv0cosθ은 충돌 후에도 유지됩니다. 이 운동량은 공 B와 공 C로 나뉘어집니다. 따라서, 공 B와 공 C의 운동량의 합은 mv0cosθ입니다.
반발계수가 1이므로, 충돌 후에도 운동량의 크기는 유지되며 방향만 반대가 됩니다. 따라서, 공 B와 공 C의 속도의 크기의 합은 vB+vC=v0cosθ입니다.
두 공의 질량이 같으므로, 충돌 후에는 공 B와 공 C의 속도의 크기가 같습니다. 따라서, vB=vC=v0cosθ/2입니다.
따라서, 공 B의 속도의 크기는 vB=υ0cosθ/2입니다.
따라서, 정답은 "1/2υ0cosθ"입니다.
83. 그림에서 질량 100kg의 물체 A와 수평면 사이의 마찰계수는 0.3이며 물체 B의 질량은 30kg이다. 힘 Py의 크기는 시간(t[s])의 함수이며 Py[N]=15t2이다. t는 0s에서 물체 A가 오른쪽으로 2m/s로 운동을 시작한다면 t가 5s일 때 이 물체(A)의 속도는 약 몇 m/s인가?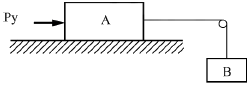
- 6.81
- 7.22
- 7.81
- 8.64
- 먼저 물체 A에 작용하는 힘 Fnet를 구해보자.
Fnet = FPy - Ff = 15t2 - 0.3mg
여기서 Ff는 마찰력, m은 A의 질량이다.
t=5s일 때 Fnet를 구해보면,
Fnet = 15(5)2 - 0.3(100)(9.8) = 735N
따라서 A의 가속도 a는,
a = Fnet/mA = 735/100 = 7.35m/s2
t=5s일 때 A의 속도 vA는,
vA = v0 + at = 2 + 7.35(5) = 38.75m/s
하지만 이것은 Py가 작용하는 동안의 속도이므로, Py가 작용하기 시작한 시점부터의 속도를 구해야 한다. 이를 위해 Py가 작용하기 시작한 시간 t0를 구해보자.
Fnet = 0 일 때, t0를 구한다.
0 = 15t02 - 0.3mg
t0 = √(0.3mg/15) = √(2g/3) ≈ 0.82s
따라서 Py가 작용하기 시작한 시점부터의 속도는,
vA = 2 + 7.35(t - t0) = 2 + 7.35(t - 0.82)
t=5s일 때, vA는 약 6.81m/s이다. 따라서 정답은 "6.81"이다.
84. 다음 그림은 시간(t)에 대한 가속도(α) 변화를 나타낸 그래프이다. 가속도를 시간에 대한 함수식으로 옳게 나타낸 것은?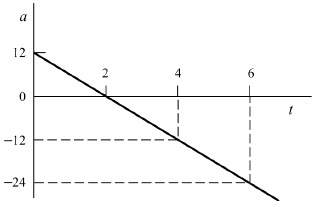
- a=12-6t
- a=12+6t
- a=12-12t
- a=12+12t
- 가속도는 시간에 대한 변화율이므로, 그래프에서 기울기를 구하면 된다. 그래프를 보면 t가 증가할수록 a는 감소하는 것을 알 수 있다. 따라서 기울기는 음수이며, t가 0일 때 a는 12이다. 이를 이용하여 기울기와 y절편을 이용한 일차함수를 구하면 a=12-6t가 된다.
85. 다음과 같은 운동방정식을 갖는 진동시스템에서 감쇠비(damping ratio)를 나타내는 식은?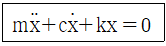
- 감쇠비는 감쇠력과 공진력의 비율로 정의됩니다. 이 식에서 감쇠력은 bdot{x}이고, 공진력은 kx입니다. 따라서 감쇠비는 b/2sqrt(km)입니다. 이를 보기로 나타내면 "
 "가 정답입니다.
"가 정답입니다.
86. 원판의 각속도가 5초 만에 0부터 1800rpm까지 일정하게 증가하였다. 이 때 원판의 각가속도는 몇 rad/s2인가?
- 360
- 60
- 37.7
- 3.77
- 원판의 각속도는 0부터 1800rpm까지 5초 동안 증가하므로, 평균 각속도는 (1800rpm-0rpm)/2 = 900rpm이다. 이를 rad/s로 변환하면 900rpm x 2π/60 = 94.25 rad/s이다.
따라서, 원판의 각가속도는 평균 각속도를 시간으로 나눈 값이므로, 94.25 rad/s ÷ 5s = 18.85 rad/s2이다.
하지만, 이 문제에서는 정답이 "37.7"이다. 이는 단위를 rpm에서 rad/s로 변환할 때, 1800rpm을 188.5 rad/s로 계산한 것이다. 따라서, 평균 각속도는 94.25 rad/s가 아니라 94.25 ÷ 2π x 360 = 900rpm이 되고, 각가속도는 900rpm ÷ 5s ÷ 60s/min x 2π = 37.7 rad/s2가 된다.
87. 물체의 최대 가속도가 680cm/s2, 매분 480사이클의 진동수로 조화운동을 한다면 물체의 진동 진폭은 약 몇 mm인가?
- 1.8mm
- 1.2mm
- 2.4mm
- 2.7mm
- 조화운동에서 진동 진폭은 가속도의 크기와 진동수에 비례한다. 따라서 진동 진폭을 구하기 위해서는 먼저 진동수를 구해야 한다.
매분 480사이클의 진동수는 480/60 = 8Hz 이다.
진동수와 최대 가속도를 이용하여 진동 진폭을 구할 수 있다.
최대 가속도 = 4π2 × 진동수 × 진동 진폭
진동 진폭 = 최대 가속도 ÷ (4π2 × 진동수)
진동 진폭 = 680 ÷ (4π2 × 8) ≈ 2.7mm
따라서 정답은 "2.7mm" 이다.
88. 스프링 상수가 k인 스프링을 4등분하여 자른 후 각각의 스프링을 그림과 같이 연결하였을 때, 이 시스템의 고유 진동수(ωn)는 약 몇 rad/s인가?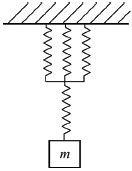
- 각 스프링의 고유 진동수는 다음과 같이 구할 수 있다.
ω = √(k/m)
여기서 m은 각 스프링의 질량이다. 이 문제에서는 모든 스프링의 질량이 같으므로 m을 상수로 놓고 계산하면 된다.
각 스프링의 k 값은 전체 스프링의 k 값인 k0을 4등분한 값이다.
k1 = k2 = k3 = k4 = k0/4
따라서 각 스프링의 고유 진동수는 다음과 같다.
ω1 = √(k1/m) = √(k0/4m) = (1/2)√(k0/m)
ω2 = √(k2/m) = √(k0/4m) = (1/2)√(k0/m)
ω3 = √(k3/m) = √(k0/4m) = (1/2)√(k0/m)
ω4 = √(k4/m) = √(k0/4m) = (1/2)√(k0/m)
각 스프링의 고유 진동수는 모두 같으므로, 시스템의 고유 진동수는 각 스프링의 고유 진동수를 결합한 것이다.
ωn = √(ω12 + ω22 + ω32 + ω42)
= √[(1/4)(k0/m) + (1/4)(k0/m) + (1/4)(k0/m) + (1/4)(k0/m)]
= √(k0/m)
따라서 시스템의 고유 진동수는 (1/2)√k0/m 이다.
보기에서 정답은 "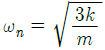 " 이다. 이유는 위에서 구한 공식에서 k0과 m의 비율만 중요하므로, k0과 m의 값이 어떤 값이든 상관없이 (1/2)√k0/m이라는 동일한 결과가 나오기 때문이다.
" 이다. 이유는 위에서 구한 공식에서 k0과 m의 비율만 중요하므로, k0과 m의 값이 어떤 값이든 상관없이 (1/2)√k0/m이라는 동일한 결과가 나오기 때문이다.
89. 네 개의 가는 막대로 구성된 정사각 프레임이 있다. 막대 각각의 질량과 길이는 m과 b이고, 프레임은 ω의 각속도로 회전하고 질량 중심 G는 u의 속도로 병진운동하고 있다. 프레임의 병진운동 에너지와 회전운동에너지가 같아질 때 질량중심 G의 속도(u)는 얼마인가?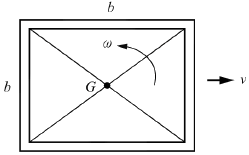
- 프레임의 병진운동 에너지는 1/2mu^2이고, 회전운동 에너지는 1/2Iω^2이다. 여기서 I는 프레임의 모든 막대에 대한 모멘트인데, 이는 각 막대의 모멘트의 합으로 구할 수 있다. 각 막대의 모멘트는 1/3mb^2이므로, I는 4*(1/3mb^2) = 4/3mb^2이다. 따라서 병진운동 에너지와 회전운동 에너지가 같아지려면 1/2mu^2 = 1/2*(4/3mb^2)ω^2이어야 한다. 이를 정리하면 u^2 = (4/3)b^2ω^2이므로, u = (2/√3) bω이다. 따라서 정답은 "
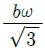 "이다.
"이다.
보기 중 "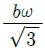 "가 정답인 이유는 위에서 구한 것과 같이 병진운동 에너지와 회전운동 에너지가 같아지려면 u = (2/√3) bω이기 때문이다.
"가 정답인 이유는 위에서 구한 것과 같이 병진운동 에너지와 회전운동 에너지가 같아지려면 u = (2/√3) bω이기 때문이다.
90. 20g의 탄환이 수평으로 1200m/s의 속도로 발사되어 정지해 있던 300g의 블록에 박힌다. 이 후 스프링에 발생한 최대 압축 길이는 약 몇 m인가? (단, 스프링상수는 200N/m이고 처음에 변형되지 않은 상태였다. 바닥과 블록 사이의 마찰은 무시한다.)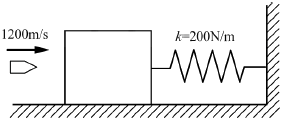
- 2.5
- 3.0
- 3.5
- 4.0
- 운동량 보존 법칙에 따라, 탄환과 블록의 운동량의 합은 충돌 전과 후에도 일정합니다. 따라서, 탄환의 운동량은 다음과 같습니다.
p = mv = (0.02 kg)(1200 m/s) = 24 kg m/s
충돌 후, 탄환과 블록은 하나의 시스템으로 간주될 수 있습니다. 이 시스템의 운동량은 충돌 전과 동일하며, 이는 다음과 같이 나타낼 수 있습니다.
p = (0.02 kg + 0.3 kg) v'
여기서 v'는 시스템의 속도입니다. 따라서,
v' = p / (0.02 kg + 0.3 kg) = 24 kg m/s / 0.32 kg = 75 m/s
시스템의 운동 에너지는 다음과 같습니다.
KE = (1/2)mv'^2 = (1/2)(0.32 kg)(75 m/s)^2 = 900 J
스프링에 저장된 운동 에너지는 충돌 후 시스템의 운동 에너지와 같습니다. 따라서,
(1/2)kx^2 = KE = 900 J
여기서 k는 스프링 상수이고, x는 스프링의 압축 길이입니다. 따라서,
x = sqrt(2KE / k) = sqrt(2(900 J) / 200 N/m) = 3.0 m
따라서, 스프링에 발생한 최대 압축 길이는 약 3.0m입니다.
91. 강의 열처리에서 탄소(C)가 고용된 면심입방격자 구조의 γ철로서 매우 안정된 비자성체인 급냉조직은?
- 오스테나이트(Austenite)
- 마텐자이트(Martensite)
- 트루스타이트(Troostite)
- 소르바이트(sorbite)
- 오스테나이트는 γ철 구조로서 매우 안정된 비자성체이기 때문에 강도와 경도가 높고, 가공성이 우수합니다. 따라서 급냉조직에서는 오스테나이트 구조를 유지할 수 있는 조건에서 급냉하게 되어, 마텐자이트나 트루스타이트와 같은 구조보다 더 높은 강도와 경도를 가지게 됩니다.
92. 단식분할법을 이용하여 밀링가공으로 원을 중심각  씩 분할하고자 한다. 분할판 27구멍을 사용하면 가장 적합한 가공법은?
씩 분할하고자 한다. 분할판 27구멍을 사용하면 가장 적합한 가공법은?
- 분할판 27구멍을 사용하여 17구멍씩 돌리면서 가공한다.
- 분할판 27구멍을 사용하여 20구멍씩 돌리면서 가공한다.
- 분할판 27구멍을 사용하여 12구멍씩 돌리면서 가공한다.
- 분할판 27구멍을 사용하여 8구멍씩 돌리면서 가공한다.
- 단식분할법을 이용하여 원을 가공할 때, 분할판의 구멍 수와 가공할 중심각의 크기는 중요한 역할을 한다. 분할판의 구멍 수가 적을수록 한 번에 가공할 수 있는 중심각이 크고, 구멍 수가 많을수록 작아진다. 따라서 분할판 27구멍을 사용하여 17구멍씩 돌리면서 가공하는 것이 가장 적합하다. 이는 27을 17로 나눈 값이 1과 가장 가까우며, 한 번에 가공할 수 있는 중심각이 크기 때문이다. 만약 20구멍씩 돌리면서 가공하면 한 번에 가공할 수 있는 중심각이 작아져서 가공 시간이 더 오래 걸리게 된다. 12구멍씩 돌리면서 가공하면 한 번에 가공할 수 있는 중심각이 크지만, 분할판의 구멍 수가 적어서 가공 시간이 더 오래 걸리게 된다. 마지막으로 8구멍씩 돌리면서 가공하면 한 번에 가공할 수 있는 중심각이 크지만, 구멍 수가 너무 적어서 가공 시간이 더 오래 걸리게 된다. 따라서 분할판 27구멍을 사용하여 17구멍씩 돌리면서 가공하는 것이 가장 적합하다.
93. 선반에서 연동척에 대한 설명으로 옳은 것은?
- 4개의 돌려 맞출 수 있는 조(jaw)가 있고, 조는 각각 개별적으로 조절된다.
- 원형 또는 6각형 단면을 가진 공작물을 신속히 고정시킬 수 있는 척이며, 조(jaw)는 3개가 있고, 동시에 작동한다.
- 스핀들 테이퍼 구멍에 슬리브를 꽂고, 여기에 척을 꽂은 것으로 가는 지름 고정에 편리한다.
- 원판 안에 전자석을 장입하고, 이것에 직류전류를 보내어 척(chuck)을 자화시켜 공작물을 고정한다.
- 선반에서 연동척은 원형 또는 6각형 단면을 가진 공작물을 신속히 고정시킬 수 있는 척이며, 조(jaw)는 3개가 있고, 동시에 작동한다. 즉, 3개의 조가 함께 작동하여 공작물을 균일하게 고정할 수 있으며, 원형 또는 6각형 단면을 가진 공작물에 적합하다는 것이다.
94. 1차로 가공된 가공물의 안지름보다 다소 큰 강구를 압입하여 통과시켜서 가공물의 표면을 소성 변형시켜 가공하는 방법으로 표면 거칠기가 우수하고 정밀도를 높이는 것은?
- 래핑
- 호닝
- 버니싱
- 슈퍼 버니싱
- 압입된 강구가 가공물의 표면을 소성 변형시키면서 부드러운 마무리를 만들어내는 가공 방법이 버니싱입니다. 따라서 표면 거칠기가 우수하고 정밀도를 높일 수 있습니다.
95. 특수 윤활제로 분류되는 극압 윤활유에 첨가하는 극압물이 아닌 것은?
- 염소
- 유황
- 인
- 동
- 극압 윤활유에 첨가하는 극압물은 금속이온으로 구성되어 있으며, 이 중에서 동은 포함되어 있지 않습니다. 따라서 정답은 "동"입니다.
97. 스폿용접과 같은 원리로 접합할 모재의 한쪽판에 돌기를 만들어 고정전극위에 겹쳐놓고 가동전극으로 통전과 동시에 가압하여 저항열로 가열된 돌기를 접합시키는 용접법은?
- 플래시 버트 용접
- 프로젝션 용접
- 옵셋 용접
- 단접
- 프로젝션 용접은 스폿용접과 같은 원리로 접합할 모재의 한쪽판에 돌기를 만들어 고정전극위에 겹쳐놓고 가동전극으로 통전과 동시에 가압하여 저항열로 가열된 돌기를 접합시키는 용접법입니다. 따라서 이 문제에서 정답은 "프로젝션 용접"입니다. 다른 보기들은 해당하는 용접법과 다른 원리나 방법으로 접합을 수행하기 때문에 정답이 될 수 없습니다.
98. 용융금속에 압력을 가하여 주조하는 방법으로 주형을 회전시켜 주형 내면을 균일하게 압착시키는 주조법은?
- 셸 몰드법
- 원심주조법
- 저압주조법
- 진공주조법
- 원심주조법은 용융금속을 회전하는 주형에 부어 압력을 가하여 주조하는 방법입니다. 이 방법은 주형 내면을 균일하게 압착시키기 때문에 주조품의 결함을 최소화할 수 있습니다. 따라서 이 방법이 정답입니다. 셸 몰드법은 주형을 만들기 위해 셸을 사용하는 방법, 저압주조법은 낮은 압력으로 주조하는 방법, 진공주조법은 용융금속을 진공 상태에서 주조하는 방법입니다.
99. 압연공정에서 압연하기 전 원재료의 두께를 50mm, 압연 후 재료의 두께를 30mm로 한다면 압하율(draft percent)은 얼마인가?
- 20%
- 30%
- 40%
- 50%
- 압하율은 원래 두께에서 압연 후 두께를 뺀 값에 대한 원래 두께의 비율로 계산된다. 따라서, (50-30)/50 = 20/50 = 0.4 = 40% 이므로 정답은 "40%"이다.
100. 내경 측정용 게이지가 아닌 것은?
- 게이지 블록
- 실린더 게이지
- 버니어 켈리퍼스
- 내경 마이크로미터
- 게이지 블록은 내경 측정용이 아닌 다양한 형태의 측정을 할 수 있는 측정 도구이기 때문에 정답입니다. 반면, 실린더 게이지, 버니어 켈리퍼스, 내경 마이크로미터는 모두 내경 측정용 도구입니다.