1과목: 수학
1. 세 실수 가 x, ,y, z가 x+y+z=4, xy+yz+zx=-14, xyz=-12를 만족시킬 때, (x+y)(y+z)(z+x)의 값은?
- -40
- -44
- -48
- -52
2. 이차방정식 x2-5x+5=0의 두 근을 α, β라고 할 때, (5α2-α3-β)(5β2-β3-α)의 값은?
- 40
- 45
- 50
- 55
3. 다항식 (2x+1)6을 4x2-1로 나누었을 때의 나머지를 R(x)라고 할 때, R(-1)의 값은?
- -32
- -16
- 16
- 32
4. 실수 x, y가 x2+y2=25를 만족시킬 때, y2+4x의 최댓값과 최솟값의 합은?
- 3
- 6
- 9
- 12
5. 두 점 A(-3, 1), B(2, 4) 와 직선 y=x 위의 점 P에 대하여 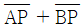 의 최솟값은? (단,
의 최솟값은? (단, 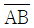 는 선분 AB의 길이이다.)
는 선분 AB의 길이이다.)
- √2
- 5√2
- 9√2
- 13√2
6. 이차함수 f(x)=-x2+2x+7에 대하여 방정식 (f(x)-a){f(x)-(a+2)}=0 이 서로 다른 세 실근을 가질 때, 상수 a의 값은?
- 2
- 4
- 6
- 8
7. 원점에서 원 x2+(y-a)2=9에 그은 두 접선이 수직일 때, 상수 a의 값은? (단, a>3 이다.)
- 3√2
- 4√2
- 5√2
- 6√2
8. x에 대한 항등식 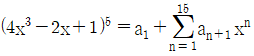 에 대하여,
에 대하여, 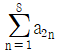 의 값은? (단, 1≤n≤16 인 자연수 n에 대하여 an은 상수이다.)
의 값은? (단, 1≤n≤16 인 자연수 n에 대하여 an은 상수이다.)
- 119
- 122
- 125
- 128
9. 유리함수 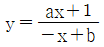 의 그래프가 두 직선 x=7, y=2와 만나지 않을 때, a+b의 값은? (단, a, b는 ab≠-1인 상수이다.)
의 그래프가 두 직선 x=7, y=2와 만나지 않을 때, a+b의 값은? (단, a, b는 ab≠-1인 상수이다.)
- 3
- 5
- 7
- 9
10. 직선 y=mx+n이 곡선 y=x2+2ax+a2+2a에 실수 a의 값에 관계없이 항상 접할 때, 점(8,3) 과 직선 y=mx+n 사이의 거리는? (단, m, n은 상수이다.)
- √5
- 2√5
- 3√5
- 4√5
11. 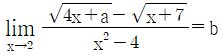 일 때, a/b의 값은? (단, a, b는 상수이고 b≠0 이다.)
일 때, a/b의 값은? (단, a, b는 상수이고 b≠0 이다.)
- 1/8
- 1/4
- 4
- 8
12. 함수 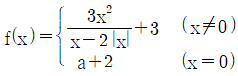 가 실수 전체의 집합에서 연속일 때, 상수 a의 값은?
가 실수 전체의 집합에서 연속일 때, 상수 a의 값은?
- 1
- 2
- 3
- 4
13. 다항함수 f(x)에 대하여 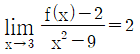 일 때, 곡선 y=f(x) 위의 점(3, f(3)) 에서의 접선의 방정식은?
일 때, 곡선 y=f(x) 위의 점(3, f(3)) 에서의 접선의 방정식은?
- y = 12x + 26
- y = 12x - 34
- y = 4x - 10
- y = 4x + 10
14. 원점을 출발하여 수직선 위를 움직이는 두 점 P,Q의 시각 t에서의 위치 x1, x2가 각각 x1=2t3-6t2, x2=3t2+24t 이다. 두 점 사이의 거리의 최댓값은? (단, 0≤t≤5 이다.)
- 68
- 95
- 112
- 128
15. 다항함수 f(x)가 임의의 두 실수 x, y에 대하여, f(x+y)=f(x)+f(y)+2xy-1 을 만족시킨다. 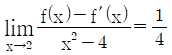 일 때, f′(2)의 값은?
일 때, f′(2)의 값은?
- -3
- -1
- 1
- 3
16. 모든 실수 x에 대하여 다항함수 f(x)는 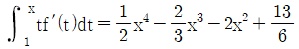 을 만족시킨다. 함수 f(x)가 x=α, β(α<β)에서 극값을 갖고 f(0)=1일 때,
을 만족시킨다. 함수 f(x)가 x=α, β(α<β)에서 극값을 갖고 f(0)=1일 때, 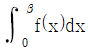 의 값은?
의 값은?
- -12
- -6
- 0
- 6
17. 함수 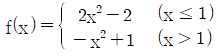 에 대하여
에 대하여 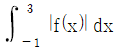 의 값은?
의 값은?
- 8
- 26/3
- 28/3
- 10
18. 집합 U={1, 2, 3, 4, 5, 6}에 대하여, 다음 세 조건을 만족시키는 순서쌍 (A, B)의 개수는?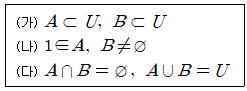
- 31
- 32
- 63
- 64
19. 한 개의 주사위를 두 번 던진다. 5의 눈이 한 번도 나오지 않을 때, 나온 두 눈의 수의 합이 3의 배수일 확률은?
- 2/25
- 4/25
- 8/25
- 16/25
20. 한 개의 주사위를 750번 던질 때, 짝수의 눈이 나오는 횟수를 확률변수 X라 하자. X의 평균을 a, 분산을 b라 할 때, a+2b의 값은? (단, a, b는 상수이다.)
- 375
- 500
- 650
- 750






또한, (x+y+z)^2 = x^2+y^2+z^2+2(xy+yz+zx) = 16이므로, x^2+y^2+z^2 = 16+2(xy+yz+zx) = -4이다.
이를 이용하여 x(y^2+z^2) + y(z^2+x^2) + z(x^2+y^2)을 계산하면, x(y^2+z^2) + y(z^2+x^2) + z(x^2+y^2) = (x+y+z)(x^2+y^2+z^2) - (x^3+y^3+z^3) = -64 - 3xyz = -28이다.
따라서, (x+y)(y+z)(z+x) = -12 - 28 + 2(xy^2+xz^2+yz^2) = -40 + 2(xy^2+xz^2+yz^2)이다.
이제 xy+yz+zx=-14를 이용하여 xy^2+xz^2+yz^2을 구해보자.
(xy+yz+zx)^2 = x^2y^2+y^2z^2+z^2x^2+2xyz(x+y+z) = (xy^2+xz^2+yz^2)xyz + 2xyz(x+y+z) + (xy+yz+zx)^2 = (xy^2+xz^2+yz^2)(-12) - 28^2 = 196
따라서, xy^2+xz^2+yz^2 = -49/3이다.
따라서, (x+y)(y+z)(z+x) = -40 + 2(xy^2+xz^2+yz^2) = -40 + 2(-49/3) = -44이다.
즉, 정답은 "-44"이다.