1과목: 수학
1. 다음 등식이 x에 대한 항등식일 때, abc의 값은? 2x2+ax+4=x(x-1)+b(x-1)(x-2)+cx(x-2) (단, a, b, c는 상수이다.)
- 10
- 20
- 30
- 40
2. 20214-1을 2020×20212+2020으로 나누었을 때의 몫은?
- 2019
- 2020
- 2021
- 2022
3. 이차방정식 x2-6x+1=0의 두 근을 α, β라고 할 때, 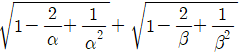 의 값은?
의 값은?
- 4√2
- 5√2
- 6√2
- 7√2
4. 이차방정식 f(x)=0의 두 근의 합이 2이고 곱이 k일 때, 함수 y=xf(x)의 그래프가 x축과 만나는 점의 개수가 2 이상이 되도록 하는 실수 k의 최댓값은?
- -1
- 0
- 1
- 2
5. 두 점 A(a, b), B(3, 4)를 이은 선분 AB 위의 점 P(1, 0)에 대하여 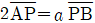 일 때, ab의 값은? (단, a, b는 상수이고
일 때, ab의 값은? (단, a, b는 상수이고 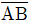 는 선분 AB의 길이이다.)
는 선분 AB의 길이이다.)
- -1
- -1/2
- 1/2
- 1
6. 원 x2+y2=25와 직선 x-y+3=0의 두 교점과 원점을 꼭짓점으로 하는 삼각형의 넓이는?
7. 중심이 (3, 4)이고 반지름이 5인 원의 방정식을 f=(x-1, y+1)=0이라고 할 때, 방정식 f(x+2, y-2)=0이 나타내는 원의 중심과 직선 x-y+3=0 사이의 거리는?
- 1
- √2
- √3
- 2√2
8. 유리함수  의 그래프와 무리함수
의 그래프와 무리함수 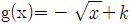 의 그래프가 한 점에서 만나도록 하는 실수 k의 최솟값은?
의 그래프가 한 점에서 만나도록 하는 실수 k의 최솟값은?
- -1/3
- 0
- 1/3
- 2/3
9. 이차방정식 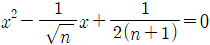 (n은 자연수)의 두 근을 αn, βn이라고 할 때,
(n은 자연수)의 두 근을 αn, βn이라고 할 때, 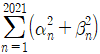 의 값은?
의 값은?
- 2018/2019
- 2019/2020
- 2020/2021
- 2021/2022
10. a1=1, nan+1=2(n+1)an (n=1, 2, 3, …) 으로 정의된 수열 {an}의 첫째항부터 제n항까지의 합을 Sn이라고 하자. S5를 10으로 나눈 나머지는?
- 6
- 7
- 8
- 9
11. 2x=5y=100z일 때, 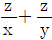 의 값은? (단, x, y, z는 xyz≠0 인 실수이다.)
의 값은? (단, x, y, z는 xyz≠0 인 실수이다.)
- 1/4
- 1/2
- 1
- 2
12. 함수 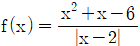 에 대하여
에 대하여 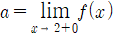 ,
, 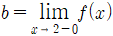 라고 할 때, ab의 값은?
라고 할 때, ab의 값은?
- -25
- -20
- -15
- -10
13. 함수 f(x)가 f(x)=x2-3x+5일 때, 함수 (x2-9)f(x)의 x=3에서의 미분계수는?
- 25
- 30
- 35
- 40
14. 함수 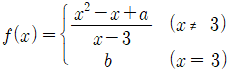 가 모든 실수 x에 대하여 연속일 때, a+b의 값은? (단, a, b는 상수이다.)
가 모든 실수 x에 대하여 연속일 때, a+b의 값은? (단, a, b는 상수이다.)
- -3
- -2
- -1
- 0
15. 곡선 y=x2-2x+3 위의 임의의 점에서 직선 y=4x-7까지의 거리 중 최단거리는?
16. 실수 a, b에 대하여 함수 f(x)가 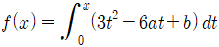 로 실수 전체의 집합에서 정의되어 있다. 함수 f(x)가 극값을 갖지 않을 때, f(1)의 최솟값은?
로 실수 전체의 집합에서 정의되어 있다. 함수 f(x)가 극값을 갖지 않을 때, f(1)의 최솟값은?
- 1/16
- 1/8
- 1/4
- 1/2
17. 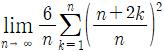 의 값은?
의 값은?
- 22
- 24
- 26
- 28
18. 수직선 위를 움직이는 어떤 물체의 시각 t에서의 속도 v(t)가 v(t)=3t2-18t+24 일 때, 시각 t=1에서 t=3까지 물체가 움직인 거리는?
- 4
- 6
- 8
- 10
19. 명중률이 각각 3/4, 2/5인 두 사람 A, B가 같은 표적을 향해 사격을 했을 때, 적어도 한 사람이 명중시킬 확률은?
- 4/5
- 17/20
- 9/10
- 19/20
20. 한 번의 시행에서 사건 A가 일어날 확률은 사건 Ac이 일어날 확률의 3배일 때, 5회의 독립시행에서 사건 A가 2회 일어날 확률은? (단, Ac은 A의 여사건이다.)
- 39/512
- 41/512
- 43/512
- 45/512






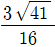
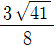
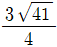
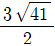
 =
= 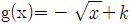
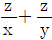 을 계산해보자. 100=102 이므로,
을 계산해보자. 100=102 이므로, 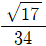
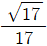

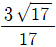
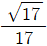 "이다.
"이다.
그리고 2021²-1은 (2021+1)(2021-1)로 인수분해할 수 있습니다.
따라서 20214-1은 (2021+1)(2021-1)(2021²+1)로 인수분해할 수 있습니다.
이제 문제에서 주어진 2020×20212+2020을 인수분해해보면 2020(2021²+1)로 나타낼 수 있습니다.
따라서, 20214-1을 2020×20212+2020으로 나누면
(2021+1)(2021-1)(2021²+1) ÷ 2020(2021²+1)
= (2021+1)(2021-1) ÷ 2020
= 2022
따라서, 몫은 2022가 됩니다.