1과목: 과목 구분 없음
1. 축이음에 대한 설명으로 옳지 않은 것은?
- 분할원통커플링은 고정커플링의 일종이다.
- 클러치는 운전 중에 단속이 가능한 축이음이다.
- 플랜지커플링은 약간의 축심 어긋남과 축의 팽창 및 수축을 흡수할 수 있다.
- 유니버설 조인트는 일반적으로 두 축이 30° 이하로 교차할 때 사용하는 축이음이다.
2. 보기의 키 중 전달 가능한 토크가 가장 큰 키와 가장 작은 키를 올바르게 짝 지은 것은? (단, 키의 종류 및 키 홈의 모양 외 나머지 조건은 동일하다)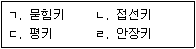
- ㄱ, ㄴ
- ㄱ, ㄷ
- ㄴ, ㄷ
- ㄴ, ㄹ
3. 리벳에 대한 설명으로 옳지 않은 것은?
- 리벳의 호칭지름은 리벳 자루의 끝부분에서 측정한다.
- 리벳구멍이 없는 판에 대한 리벳구멍이 있는 판의 인장강도 비를 판의 효율이라고 한다.
- 리벳의 머리모양에 따라 둥근머리, 접시머리, 납작머리, 냄비머리, 둥근접시머리 리벳 등으로 구분한다.
- 보일러와 같이 기밀이 필요할 때는 리벳머리 둘레와 강판의 가장자리를 정과 같은 공구로 코킹작업을 한다.
4. 용접이음에 대한 설명으로 옳지 않은 것은?
- 용접의 종류에는 압접, 융접 등이 있다.
- 열응력에 의한 잔류변형이 생기지 않는다.
- 정밀한 작업 시 작업자의 숙련도가 요구된다.
- 리벳이음에 비하여 기밀성과 수밀성이 양호하다.
5. 안쪽 반지름이 2m이며 두께가 얇은 원통형 압력 용기에서 원통 벽면의 원주방향 허용응력이 80MPa이다. 다음 중 1,000kPa의 내압이 작용할 때, 원주방향 허용응력을 넘지 않는 조건에서 최소 벽 두께[mm]에 가장 가까운 값은?
- 15
- 30
- 45
- 60
6. 길이 50 mm, 지름 20mm, 포아송비(ν) 0.3인 봉에 1,200kN의 인장하중이 작용하여 봉의 횡방향 압축변형률(εd)이 0.006이 되었을 때, 이 봉의 세로탄성계수 E[GPa]는? (단, π=3이고 봉의 변형은 비례한도 내에 있다)
- 100
- 150
- 200
- 250
7. 벨트의 장력비 1.6, 벨트의 이완측 장력 500N, 벨트의 허용응력 1MPa, 벨트의 폭 10cm, 벨트의 이음효율 80%일 때, 필요한 벨트의 최소 두께[mm]는? (단, 벨트의 원심력 및 굽힘응력은 무시한다)
- 5
- 10
- 15
- 20
8. 원동차와 종동차의 지름이 각각 200mm, 600mm이며 서로 외접하는 원통마찰차가 있다. 원동차가 1,200rpm으로 회전하면서 종동차를 10kN으로 밀어붙여 접촉한다면 최대 전달동력[kW]은? (단, 마찰계수는 μ=0.2이다)
- 2π
- 4π
- 8π
- 12π
9. 접촉면 평균지름(Dm)이 200mm, 면압이 0.2 N/mm2인 단판 마찰클러치가 80πN⋅m의 토크를 전달하기 위해 필요한 접촉면의 최소 폭(b)[mm]은? (단, 접촉면의 마찰계수는 μ=0.2이고, 축방향 힘은 균일 압력조건, 토크는 균일 마모조건으로 한다)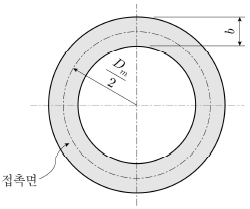
- 5
- 10
- 50
- 100
10. 강도를 고려하여 지름 d인 끝저널(엔드저널)을 설계하기 위해 베어링 폭이 l인 미끄럼베어링 내의 평균압력 pm을 길이 l인 저널 중앙지점에 작용하는 집중하중 P로 대체하고 저널을 외팔보로 취급하여 설계한다면 l/d은? (단, 저널의 허용굽힘응력은 σa이다)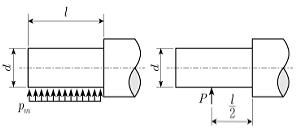
11. 외접하는 표준 스퍼기어 두 개의 잇수가 각각 40, 60개이고 원주피치가 3πmm일 때, 두 축 사이의 중심거리[mm]는?
- 100
- 150
- 200
- 250
12. 클러치의 종류에 관한 설명으로 옳지 않은 것은?
- 맞물림클러치: 양쪽의 턱이 서로 맞물려서 미끄럼 없이 동력이 전달된다.
- 원심클러치: 원동축의 원심력으로 전자코일에서 기전력을 발생시켜 동력을 전달한다.
- 유체클러치: 일정한 용기 속에 유체를 넣어서 구동축을 회전시키면 유체를 통해 종동축에 동력이 전달된다.
- 마찰클러치: 원동축과 종동축에 붙어 있는 접촉면을 서로 접촉시킬 때 발생하는 마찰력에 의해 동력을 전달한다.
13. 전위기어의 사용 목적으로 옳지 않은 것은?
- 언더컷을 방지하려고 할 때 사용한다.
- 최소 잇수를 줄이려고 할 때 사용한다.
- 물림률을 감소시키려고 할 때 사용한다.
- 이의 강도를 증가시키려고 할 때 사용한다.
14. 원통 또는 원뿔의 플러그를 90° 회전시켜 유체의 흐름을 개폐시킬 수 있는 밸브는?
- 콕
- 스톱밸브
- 슬루스밸브
- 버터플라이밸브
15. 짝 지어진 두 개의 물리량을 SI 기본단위(m, kg, s)로 환산할 경우, 동일한 단위로 연결되지 않은 것은?
- PS -J
- mmHg -Pa
- kgf/m2 - N/m2
- kgf⋅m/s -W
16. 다음 그림은 두 개의 기어로 이루어진 감속장치 개념도이다. 입력축은 10rad/s의 각속도로 10kW의 동력을 받아 모듈 5mm, 압력각 30°인 두 개의 표준 스퍼기어(G1, G2)를 통하여 출력축으로 내보낸다. 입력축에서 G1 기어와 B1, B2 베어링 사이의 수평거리가 각각 100mm일 때, B1 베어링에 작용하는 하중[N]은? (단, 입력축 G1 기어의 잇수는 40개이다)
- 5,000
- 5,000 / √3
- 10,000 / √3
- 20,000 / √3
17. 동일 재료로 제작된 길이 l, 지름 d인 중실축과 길이 2l, 지름 2d인 중실축이 각각 T1과 T2의 비틀림 모멘트를 받아 동일한 비틀림각이 발생하였다면 T1/T2은?
- 1/2
- 1/4
- 1/8
- 1/16
18. 나사산 높이가 2mm이고 바깥지름이 40mm이며, 2회전할 때 축 방향으로 8mm 이동하는 한 줄 사각나사가 있다. 나사를 조일 때 나사 효율은? (단, 마찰각은 ρ이며, 자리면 마찰은 무시한다)
19. 질량 40kg인 원판형 플라이휠이 장착된 절단기는 강판을 한 번 절단할 때 플라이휠의 회전속도가 2,000rpm에서 1,000rpm으로 줄어들어 30kJ의 운동에너지가 소모된다. 이 플라이휠의 반지름[m]은? (단, π=3이고, 플라이휠의 재료는 균일하다)
- 1/√5
- 1/√10
- 1/√20
- 1/√40
20. 다음 그림과 같이 길이가 l이며 폭, 높이가 각각 b, h인 직사각형 단면으로 한쪽 끝이 고정된 단판스프링이 있다. 다른 한쪽 끝에 수직하중 P가 작용할 때, 단판스프링에 작용하는 최대굽힘응력 σmax와 끝단 처짐에 따른 등가 스프링상수 k는? (단, E는 단판스프링 재료의 세로탄성계수이다)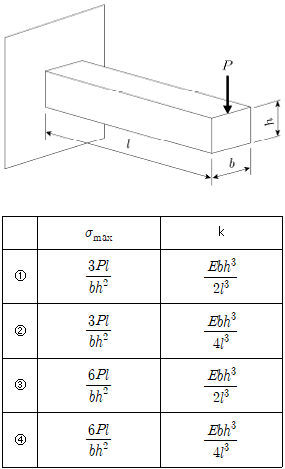
- ①
- ②
- ③
- ④






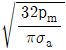
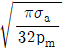
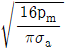
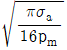
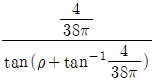
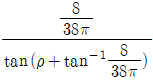
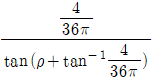

플랜지커플링은 약간의 축심 어긋남과 축의 팽창 및 수축을 흡수할 수 있습니다. 이는 커플링 내부의 유연한 소재로 인해 가능합니다. 따라서 축의 진동이나 축의 이동에도 유연하게 대처할 수 있습니다.
분할원통커플링은 고정커플링의 일종으로, 두 축을 정확하게 일직선으로 맞추어 연결하는 역할을 합니다.
유니버설 조인트는 두 축이 서로 다른 각도로 교차할 때 사용하는 축이음입니다. 이는 자동차의 구동축과 바퀴축을 연결하는데 사용됩니다.
반면, 클러치는 엔진과 변속기 사이에 위치하여 엔진의 동력을 변속기로 전달하거나 차량을 정지시키는 역할을 합니다. 축이음과는 관련이 없습니다.