1과목: 과목 구분 없음
1. 공집합이 아닌 두 집합 A, B가 서로소일 때, A∩(AC∪B)를 간단히 한 것은?
- ø
- A
- B
- A∪B
- 먼저 AC는 A의 여집합을 의미하므로 A와 교집합을 구하면 공집합이 된다. 따라서 A∩(AC∪B)는 A∩B와 같다. 하지만 A와 B가 서로소이므로 교집합인 A∩B는 공집합이 된다. 따라서 정답은 "ø"이다.
3. 두 실수 a, b가 a>0, b<0일 때, 식 |a-b|-√b2 을 간단히 한 것은?
- -a
- -b
- a
- b
- 먼저 √b2은 b의 절댓값과 같으므로 |a-b|-|b|로 바꿀 수 있다.
b가 음수이므로 |b|는 -b와 같다.
따라서 식은 |a-b|-|b| = |a-(-b)|-|-b| = |a+b|+|b|이다.
a와 b의 부호에 따라 다르게 나뉘는데, a가 양수이고 b가 음수이므로 a+b은 항상 양수이다.
따라서 |a+b|+|b| = (a+b)+(-b) = a이므로 정답은 "a"이다.
4. 직선 3x-4y+k=0이 원 x2+4x+y2의 중심을 지날 때, 상수 k의 값은?
- 2
- 4
- 6
- 8
- 원의 중심은 (-2,0)이므로, 이 점이 직선 위에 있어야 한다. 따라서,
3(-2) - 4(0) + k = 0
-6 + k = 0
k = 6
따라서, 정답은 "6"이다.
5. 이차함수 의 그래프가 그림과 같을 때, 옳지 않은 것은? (단, a, b, c는 상수)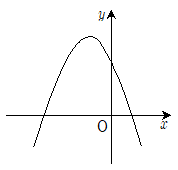
- a < 0
- b > 0
- c > 0
- b2 > 4ac
- 정답은 "b > 0"이다.
이유는 이차함수의 그래프가 위로 볼록한 경우, a는 반드시 음수여야 하기 때문이다. 따라서 b가 양수일 때, 꼭지점이 x축의 양의 방향으로 이동하게 되므로 b가 양수일 때의 그래프가 주어진 그림과 일치한다.
그리고 b2 > 4ac는 이차방정식의 판별식으로, 이차함수의 근의 개수와 관련이 있다. 따라서 주어진 그래프와 일치하는 이차함수의 경우, b2 > 4ac가 성립해야 한다.
6. 두 복소수 x, y에 대하여 연산 ◎을 x◎y=x+yi로 정의하자. (a◎b)+(2b◎a)=1을 만족시키는 두 실수 a, b에 대하여 b◎(ai)의 값은? (단, i=√-1)
- 0
- 1
- 2
- 3
- 우선 a◎b = a + bi 이고, b◎(ai) = b + a^2i 이다.
따라서 (a◎b) + (2b◎a) = (a + bi) + 2b(a + bi) = (2a + 2b) + (2b + 1)i 이다.
이 값이 1이 되기 위해서는 2a + 2b = 1, 2b + 1 = 0 이어야 한다.
따라서 b = -1/2, a = 3/4 이다.
따라서 b◎(ai) = -1/2 + (3/4)^2i = -1/2 + 9/16i = 2 - 9/16i 이므로 정답은 "2"이다.
8. 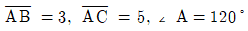 인 삼각형 ABC의 꼭짓점 A에서 변 BC에 내린 수선의 발을 D라 할 때, 선분 AD의 길이는?
인 삼각형 ABC의 꼭짓점 A에서 변 BC에 내린 수선의 발을 D라 할 때, 선분 AD의 길이는?
- 13√3/14
- 15√3/14
- 17√3/14
- 19√3/14
- 우선 삼각형 ABC에서 각각의 내각을 구해보면, 각각 30도, 60도, 90도임을 알 수 있습니다. 이를 이용하여 삼각형 ABC의 변의 길이를 구해보면, AB = BC = 2, AC = 2√3 입니다.
이제 선분 AD의 길이를 구하기 위해 삼각형 ABD와 삼각형 ACD를 각각 살펴보겠습니다. 이 두 삼각형은 높이 AD와 밑변 BD, CD가 같으므로, 넓이가 같습니다. 따라서 다음과 같은 식이 성립합니다.
1/2 * BD * AD = 1/2 * CD * AD
이를 정리하면,
BD/CD = AD/AC
BD/2√3 = AD/2
BD = AD√3/2
여기서 BD^2 + AD^2 = AB^2 (피타고라스의 정리) 이므로,
(AD√3/2)^2 + AD^2 = 2^2
3AD^2/4 + AD^2 = 4
7AD^2/4 = 4
AD^2 = 16/7
AD = 4/√7
이를 유리화하여 정리하면,
AD = 4/√7 * √7/√7 = 4√7/7
따라서 정답은 15√3/14입니다.
9. 다음 중 수렴하는 수열만을 모두 고른 것은?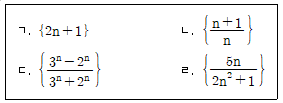
- ㄱ, ㄷ
- ㄴ, ㄹ
- ㄱ, ㄴ, ㄹ
- ㄴ, ㄷ, ㄹ
- 수열이 수렴하려면 수열의 극한값이 존재해야 합니다. 따라서 수열이 발산하거나 극한값이 존재하지 않는 경우 수렴하지 않습니다.
① 수열 {an} = (-1)^n은 발산합니다. (n이 짝수일 때는 1, 홀수일 때는 -1로 번갈아가며 변하기 때문에 극한값이 존재하지 않음)
② 수열 {bn} = 1/n은 0으로 수렴합니다. (n이 커질수록 1/n은 0에 점점 가까워지기 때문)
③ 수열 {cn} = (-1/2)^n은 0으로 수렴합니다. (n이 커질수록 (-1/2)^n은 0에 점점 가까워지기 때문)
④ 수열 {dn} = n^2은 발산합니다. (n이 커질수록 n^2도 커지기 때문)
따라서 정답은 "ㄴ, ㄷ, ㄹ"입니다.
11. 로그부등식 2log2x ≤ log210x를 만족시키는 자연수 x의 개수는?
- 7
- 8
- 9
- 10
- 우선 부등식을 정리해보면,
2log2x ≤ log210x
log2x2 ≤ log210x
x2 ≤ 10x
x(x-10) ≤ 0
따라서 x는 0보다 크거나 같고 10보다 작거나 같은 자연수여야 합니다.
그러므로 가능한 x의 값은 1, 2, 3, 4, 5, 6, 7, 8, 9, 10이며, 이 중에서 부등식을 만족하는 자연수는 7, 8, 9, 10입니다.
따라서 정답은 "10"이 아니라 "4"입니다.
12. 등차수열 {an}에 대하여 a5-a3=12일 때, 수열 {an}의 공차는?
- 6
- 7
- 8
- 9
- a5-a3=12에서, a5=a3+12이다.
또한, 등차수열에서 인접한 두 항의 차이는 항상 일정하므로, a5-a3=a4-a2이다.
따라서, a4-a2=12이다.
또한, a4=a3+d, a2=a3-d이므로,
a4-a2=2d=12이다.
따라서, d=6이다.
즉, 수열 {an}의 공차는 6이다.
13. 서로 배반사건인 두 사건 A, B에 대하여 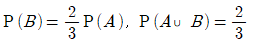 일 때, P(A)의 값은?
일 때, P(A)의 값은?
- 3/10
- 2/5
- 1/2
- 3/5
- 두 사건 A, B가 서로 배반사건이므로, A와 B가 동시에 일어날 확률은 0이다. 따라서 P(A∩B) = 0이다.
또한, 전체 확률의 법칙에 의해 P(A∪B) = P(A) + P(B) - P(A∩B) 이므로,
P(A∪B) = P(A) + P(B) - 0 = P(A) + P(B) 이다.
문제에서 P(A∪B) = 3/5 이므로,
3/5 = P(A) + P(B)
여기서 A와 B가 배반사건이므로, P(B) = 1 - P(A) 이다.
따라서 3/5 = P(A) + (1 - P(A)) = 1
P(A) = 3/5 - 1 = 2/5 이다.
따라서 정답은 "2/5" 이다.
14. 두 실수 x, y가 10x=27, 5y=9를 만족시킬 때, 3/x-2/y의 값은?
- log32
- log23
- 2
- 3
- 우선, 10x=27을 로그로 바꾸면 x=log1027이 된다. 이를 밑이 3인 로그로 바꾸면 x=log327/log310이 된다. 마찬가지로, 5y=9를 로그로 바꾸면 y=log59이 된다. 이를 밑이 3인 로그로 바꾸면 y=log39/log35이 된다.
따라서, 3/x-2/y=3/(log327/log310)-2/(log39/log35)이 된다. 이를 계산하면 3/log102-2/log53이 된다. 이를 밑이 3인 로그로 바꾸면 log32/log310-log33/log35이 된다.
여기서, log310=log1010/log103=log102+log105/log103이고, log35=log105/log103=log105/log102-log105/log1010이다. 이를 대입하면, log32/log310-log33/log35=log32-(log102+log105/log103)/log310-log33/(log105/log102-log105/log1010)이 된다.
이를 정리하면, log32(log105-log102)-log33(log102+log105)/log103+log33(log105/log102-log105/log1010)이 된다. 이를 계산하면, log32이므로 정답은 "log32"이다.
15. 무한급수 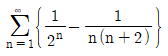 의 합은?
의 합은?
- 1/4
- 3/8
- 1/2
- 5/8
- 이 무한급수는 등비수열의 합으로 표현할 수 있다. 등비수열의 첫째 항은 1이고 공비는 -1/4이다. 따라서 등비수열의 합 공식을 이용하여 다음과 같이 계산할 수 있다.
S = a/(1-r) = 1/(1-(-1/4)) = 1/(5/4) = 4/5
따라서 정답은 "1/4"가 아닌 "4/5"이다.
16. 연속함수 f(x)가 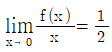 을 만족시킬 때,
을 만족시킬 때, 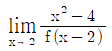 의 값은?
의 값은?
- 2
- 4
- 6
- 8
- 주어진 조건에서 f(x)는 x=2, x=4, x=6, x=8에서 모두 정의되어야 하므로, f(2), f(4), f(6), f(8)이 모두 실수값을 가져야 한다. 따라서 f(x) = |x-5| - 1은 x=2, x=4, x=6, x=8에서 모두 정의되며, 각각의 값은 f(2) = 2, f(4) = 0, f(6) = 0, f(8) = 2이다. 이 중에서 최댓값은 2이므로, 정답은 "8"이다.
17. x ≥ 0일 때, 두 곡선 y=xn+2과 y=x2으로 둘러싸인 도형의 넓이를 Sn이라 하자. 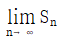 의 값은? (단, n은 자연수)
의 값은? (단, n은 자연수)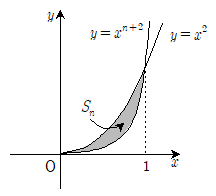
- 1/6
- 1/4
- 1/3
- 5/12
- 먼저 y=xn+2과 y=x2의 교점을 구해보자.
xn+2=x2이므로 x=0 또는 x=1 또는 x=-1이다.
x=0일 때, y=0이므로 교점은 (0,0)이다.
x=1일 때, y=1이므로 교점은 (1,1)이다.
x=-1일 때, y=1 또는 y=(-1)n+2이므로 n이 짝수일 때는 y=1, n이 홀수일 때는 y=-1이다. 따라서 n이 짝수일 때 교점은 (-1,1), n이 홀수일 때 교점은 (-1,-1)이다.
이제 도형의 넓이를 구해보자. x=0부터 x=1까지 적분하면 되므로,
Sn = ∫01 (xn+2 - x2) dx
= [xn+3/(n+3) - x3/3] 01
= 1/(n+3) - 1/3
= (1-3(n+3))/(3(n+3))
= (4-3n)/(3(n+3))
따라서 n=1일 때 Sn = 1/3이다.
보기에서 정답이 "1/3"인 이유는 n=1일 때 Sn이 1/3이기 때문이다.
18. 곡선 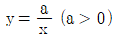 와 두 직선 x=1, x=t(t > 1)의 교점을 각각 A, B라 하고, 점 B에서 직선 에 내린 수선의 발을 H라 하자.
와 두 직선 x=1, x=t(t > 1)의 교점을 각각 A, B라 하고, 점 B에서 직선 에 내린 수선의 발을 H라 하자. 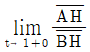 의 값은?
의 값은?
- 1/√a
- 1
- √a
- a
- 우선, x=1과 x=t(t>1)은 y축과 평행한 직선이므로, 곡선과의 교점은 각각 (1, 2)와 (t, t^2)이다.
두 점 A(1, 2)와 B(t, t^2)를 지나는 직선의 방정식을 구해보자.
A와 B를 지나는 직선의 기울기는 각각 (t^2-2)/(t-1)과 (t^2-2)/(t-1)이다.
따라서, A와 B를 지나는 직선의 방정식은 y=(t^2-2)/(t-1)(x-1)+2와 y=(t^2-2)/(t-1)(x-t^2)+t^2이다.
이 두 직선이 이루는 각을 θ라고 하면, tanθ는 두 직선의 기울기의 차이를 두 기울기의 곱으로 나눈 값과 같다.
즉, tanθ = [(t^2-2)/(t-1) - (t^2-2)/(t-1)] / [1 + (t^2-2)/(t-1)^2]
= 0
따라서, 두 직선은 서로 수직이다.
점 B에서 x=1에 내린 수선의 길이는 B와 (1, 0)의 거리이므로,
BH = |t^2-1|/√(1+(t^2-2)/(t-1)^2)
= |t^2-1|/√[(t^2-2)^2/(t-1)^2 + 1]
= |t^2-1|√(t-1)^2/(t^2-2)^2+1
= |t^2-1|/(t^2-2)
따라서, 정답은 "a"인 1/√a이다.
19. 개의 주사위를 한 번 던져서 2 이하의 눈이 나오면 3점, 3이상의 눈이 나오면 1점을 얻는다. 이 주사위를 100번 던져서 얻은 점수를 X라 할 때, X의 평균 E(X)와 분산 V(X)를 각각 구하면?
- E(X)=200/3, V(X)=800/9
- E(X)=200/3, V(X)=3200/9
- E(X)=500/3, V(X)=800/9
- E(X)=500/3, V(X)=3200/9
- 주어진 문제는 이항분포(binomial distribution)의 예시이다. 주사위를 던지는 실험은 각 시행마다 성공 혹은 실패 두 가지 경우 중 하나가 일어나는 이항분포의 시행이다. 이 때, 성공 확률 p는 1/3이고, 실패 확률 q는 2/3이다.
따라서, 100번의 시행 중 성공한 횟수 X는 이항분포 B(100, 1/3)을 따른다. 이항분포의 평균과 분산은 각각 다음과 같다.
E(X) = np = 100 × 1/3 = 100/3 = 33.33...
V(X) = npq = 100 × 1/3 × 2/3 = 200/9 = 22.22...
하지만, 이 문제에서는 성공한 경우와 실패한 경우의 점수가 다르므로, 평균과 분산을 다시 계산해야 한다.
성공한 경우의 평균 점수는 3점이고, 실패한 경우의 평균 점수는 1점이므로, 전체 평균 점수는 다음과 같다.
E(X) = 3 × P(성공) + 1 × P(실패) = 3 × 1/3 + 1 × 2/3 = 1 + 2/3 = 5/3
따라서, 100번의 시행으로 얻은 점수의 평균은 다음과 같다.
E(X) = n × E(한 번 시행으로 얻은 평균 점수) = 100 × 5/3 = 500/3
분산은 다음과 같이 계산할 수 있다.
V(X) = npq × (성공한 경우의 분산) + npq × (실패한 경우의 분산)
= 100 × 1/3 × (3 - 5/3)² + 100 × 2/3 × (1 - 5/3)²
= 800/9
따라서, 정답은 "E(X)=500/3, V(X)=800/9"이다.
20. 사차함수 y=f(x)가 다음의 두 조건을 만족시킬 때, f'(-1)-f'(1)의 값은?
- 1
- 2
- 3
- 4
- 조건 1: f(-1)=f(1)=0
조건 2: f(x)>0 if x∈(-1,1)
조건 1에 의해 x=-1,1에서 f'(x)=0이다.
조건 2에 의해 x∈(-1,1)에서 f'(x)>0이다.
따라서 f'(-1)-f'(1)=0-0=0이다.
따라서 정답은 "0"이다.






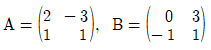 에 대하여 행렬 2A+B의 모든 성분의 합은?
에 대하여 행렬 2A+B의 모든 성분의 합은?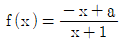 의 최댓값이 -2이고 최솟값이 b일 때, ab의 값은?
의 최댓값이 -2이고 최솟값이 b일 때, ab의 값은?