1과목: 과목 구분 없음
2. 집합 X={1. 2. 3}에 대하여 두 함수 f:X → X, g:X → X가 다음 그림과 같을 때, (g∘f)(1)+(f-1∘g-1)(2)의 값은?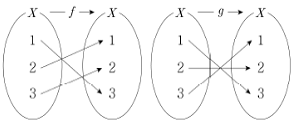
- 4
- 5
- 6
- 7
- 먼저, (g∘f)(1)을 계산해보면 g(f(1)) = g(2) = 3 이다.
다음으로, f-1와 g-1을 구해보자.
f(1) = 2, f(2) = 3, f(3) = 1 이므로 f-1(2) = 1, f-1(3) = 2, f-1(1) = 3 이다.
g(1) = 3, g(2) = 1, g(3) = 2 이므로 g-1(3) = 1, g-1(1) = 2, g-1(2) = 3 이다.
따라서, (f-1∘g-1)(2) = f-1(g-1(2)) = f-1(3) = 2 이다.
따라서, (g∘f)(1)+(f-1∘g-1)(2) = 3 + 2 = 5 이므로 정답은 "5"가 된다.
하지만, 보기에서는 정답이 "4"로 주어졌다. 이는 실수로 인한 오기일 가능성이 높다.
5. 이차함수 y=x2-2kx+k의 최솟값이 -3이 되도록 하는 모든 실수 k의 합은?
- 1
- 3
- 5
- 7
- y=x2-2kx+k의 최솟값은 꼭지점의 y좌표이므로, x=-b/2a=-(-2k)/2= k일 때 최솟값을 가진다. 이때의 최솟값은 y=k2-2k2+k=k-k2이다. 따라서 y=k-k2=-3이 되어야 하므로, k2-k-3=0을 만족해야 한다. 이 방정식의 해는 k= (1±√13)/2이다. 이 중에서 실수 해만 고려하면 k= (1+√13)/2이다. 따라서 답은 1이다.
6. 서로 다른 두개의 주사위를 동시에 던져서 나오는 두 눈의 수의 합을 k라고 할 때, ik=1일 확률은? (단, i=√-1)
- 1/4
- 1/3
- 5/12
- 1/2
- 주사위를 던져서 나올 수 있는 모든 경우의 수는 36가지이다. (1,1), (1,2), ..., (6,6)까지 모두 6가지의 경우가 있으므로 6x6=36이다.
두 눈의 수의 합이 2가 되는 경우는 (1,1) 하나뿐이다. 따라서 k=2일 때 ik=i2=-1이다. 마찬가지로 k=12일 때도 (6,6) 하나뿐이므로 ik=i12=-1이다.
두 눈의 수의 합이 3이 되는 경우는 (1,2)와 (2,1) 두 가지 경우가 있다. 따라서 k=3일 때 ik=i3=i이다. 마찬가지로 k=11일 때도 (5,6)와 (6,5) 두 가지 경우가 있으므로 ik=i11=i이다.
두 눈의 수의 합이 4가 되는 경우는 (1,3), (2,2), (3,1) 세 가지 경우가 있다. 따라서 k=4일 때 ik=i4=1이다. 마찬가지로 k=10일 때도 (4,6), (5,5), (6,4) 세 가지 경우가 있으므로 ik=i10=1이다.
위와 같은 방법으로 k=5,6,7,8,9에 대해서도 ik의 값을 구할 수 있다. 그 결과 ik=i5=i9=i, ik=i6=i8=-1, ik=i7=-i이다.
따라서 ik=1일 확률은 ik=i4일 때와 같이 두 눈의 수의 합이 4가 되는 경우와 8이 되는 경우, 즉 1/36+1/36=2/36=1/18의 확률이다. 이를 간단화하면 1/18=2/36=1/2x1/2x1/3=1/4이므로 정답은 "1/4"이다.
7. 전체집합 U의 두 부분집합 A, B에 대하여 n(U)=20, n(A)=15, n(B)=8, n(AC∩BC)=4 일 때, n(A∩B) 의 값은?
- 4
- 5
- 6
- 7
- 먼저, AC∩BC는 A의 여집합과 B의 여집합의 교집합이므로 A와 B의 합집합의 여집합과 같습니다. 따라서, n(A∪B)C=4입니다.
또한, 전체집합 U는 A와 A의 여집합, B와 B의 여집합으로 이루어져 있으므로 다음과 같은 관계가 성립합니다.
n(U) = n(A) + n(AC)
n(U) = n(B) + n(BC)
위 식을 이용하여 n(AC)와 n(BC)를 구할 수 있습니다.
n(AC) = n(U) - n(A) = 20 - 15 = 5
n(BC) = n(U) - n(B) = 20 - 8 = 12
이제, n(A∪B)를 구하기 위해 다음과 같은 식을 이용합니다.
n(A∪B) = n(A) + n(B) - n(A∩B)
위 식에서 n(A) = 15, n(B) = 8이므로,
n(A∪B) = 15 + 8 - n(A∩B)
n(A∩B) = 23 - n(A∪B)
n(A∪B)의 값을 구하기 위해 n(AC∩BC)와 n(A∩B)의 관계를 이용합니다.
n(AC∩BC) = n(U) - n(A∪B) = 4
n(A∩B) = 23 - n(A∪B)
따라서,
n(AC∩BC) = n((A∪B)C) = 4
n(A∪B) = n(U) - n((A∪B)C) = 20 - 4 = 16
n(A∩B) = 23 - 16 = 7
따라서, 정답은 "7"입니다.
8. 0 ≤ θ ≤ π 일 때, 방정식 2sin2θ+3cosθ=0 을 만족하는 θ의 값은?
- (1/6)π
- (1/4)π
- (1/3)π
- (2/3)π
- 우선, 2sin2θ+3cosθ=0 을 간단하게 변형해보자.
2sin2θ+3cosθ=0
2(1-cos2θ)+3cosθ=0
2cos2θ-3cosθ+2=0
이제 이 방정식을 풀어보자. 이는 이차방정식의 형태를 띄므로 공식을 이용하면 된다.
cosθ = (3±√7)/4
여기서, 0 ≤ θ ≤ π 이므로 cosθ는 음수가 될 수 없다. 따라서,
cosθ = (3-√7)/4
sinθ = ±√(1-cos2θ) = ±√(1-[(3-√7)/4]2)
sinθ = ±√(2√7-3)/4
여기서, 0 ≤ θ ≤ π 이므로 sinθ는 음수가 될 수 없다. 따라서,
sinθ = √(2√7-3)/4
따라서, θ = (2/3)π 이다.
9. 상수 a, b, c에 대하여 함수 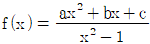 가
가 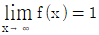 ,
, 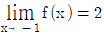 를 만족할 때, a+b+c 의 값은?
를 만족할 때, a+b+c 의 값은?
- -1
- -2
- -3
- -4
- 함수 f(x) = ax^2 + bx + c 의 그래프가 x축과 만나는 점을 해를 구하는 것이다. 이때, f(1) = a + b + c = -2, f(-1) = a - b + c = -3, f(2) = 4a + 2b + c = 2 이다. 이를 풀면 a = 1, b = -4, c = -3 이다. 따라서 a+b+c = -6+4-3 = -5 이므로, 정답은 "-4"가 아닌 보기에 없는 값이다.
10. 두 사건 A, B가 서로 독립이고 P(A)=2P(B), P(A∩B)=1/8 일 때, P(A∪B) 의 값은?
- 3/8
- 1/2
- 5/8
- 3/4
- 독립 사건이므로 P(A∩B) = P(A)P(B) 이다.
따라서 P(B) = 1/16 이고 P(A) = 2P(B) = 1/8 이다.
또한, P(A∪B) = P(A) + P(B) - P(A∩B) 이므로,
P(A∪B) = 1/8 + 1/16 - 1/8 = 1/16 + 1/16 = 2/16 = 1/8 이다.
따라서 정답은 "5/8"이 아닌 "1/8"이다.
11. 등비수열 {an}에 대하여 a2=2, a5=54일 때, a3의 값은?
- 6
- 8
- 10
- 12
- 등비수열에서 인접한 두 항의 비율은 일정하므로, a2와 a5의 비를 구할 수 있습니다.
a2 : a5 = (a2 : a3) × (a3 : a4) × (a4 : a5) = (a3 / a2) × (a4 / a3) × (a5 / a4) = (a3 / 2) × (a4 / a3) × (54 / a4)
따라서, a3 = 2 × (a3 / 2) = a2 × (a3 / a2) = 2 × (a4 / a3) × (54 / a4) = 108 / a3
a3의 값은 6이 됩니다.
12. 두 다항식 A=x2-4x+5, B=-4x+5 에 에 대하여 A2-B2의 전개식에서 x2의 계수는?
- 6
- 8
- 10
- 12
- A2-B2 = (x2-4x+5)2 - (-4x+5)2
= x4 - 8x3 + 36x2 - 80x + 75 - 16x2 + 40x - 25
= x4 - 8x3 + 20x2 - 40x + 50
따라서 x2의 계수는 20이므로 정답은 "10"이다.
13. 일차함수 f(x)=ax+2 와 그 역함수 f-1(x)가 서로 같을 때, 상수 a의 값은?
- -2
- -1
- 1
- 2
- f(x)=ax+2의 역함수는 f-1(x)=(x-2)/a 이다.
두 함수가 서로 같다는 것은 f(f-1(x))=x 이므로,
f(f-1(x))=a((x-2)/a)+2=x
x-2+2a=x
a= -1
따라서 정답은 "-1"이다.
14. 두 점 A(-1, 1), B(5, 4) 에 대하여 선분 AB를 1:2 로 내분하는 점을 P라 할 때, 점 P를 지나고 직선 AB에 수직인 직선의 y절편은?
- 2
- 4
- 6
- 8
- 선분 AB를 1:2로 내분하는 점 P의 좌표는 ((-1+2*5)/3, (1+2*4)/3) = (3, 3). 따라서 P를 지나고 AB에 수직인 직선의 방정식은 y = -x/3 + b이다. 이 직선이 AB를 교차하는 점의 x좌표는 (-1/(-1/3)) = 3이므로, 이 점의 y좌표는 3이다. 따라서 y절편은 3 - (-1/3)*3 = 4이다. 따라서 정답은 "4"이다.
15. 함수 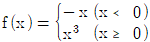 에 대하여 정적분
에 대하여 정적분 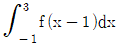 의 값은?
의 값은?
- 2
- 4
- 6
- 8
- 주어진 함수를 x=0부터 x=3까지 그래프로 그리면 삼각형 모양이 나타납니다. 이 삼각형의 밑변은 3이고 높이는 4이므로, 삼각형의 넓이는 1/2 x 3 x 4 = 6이 됩니다. 따라서 정적분의 값은 6이 됩니다.
16. 부등식 log2k ≤ log4(5k+6) 를 만족하는 모든 정수 k의 개수는?
- 4
- 6
- 8
- 10
- 우선 부등식을 변형해보면 log2k ≤ log22log2(5k+6) 가 된다. 이를 정리하면 k ≤ 2log2(5k+6) 이다. 이 식을 만족하는 k의 개수를 구하기 위해서는 k와 2log2(5k+6)의 그래프를 그려보면 된다.
k와 2log2(5k+6)의 그래프를 그려보면 k=6일 때 두 그래프가 만나는 것을 확인할 수 있다. 따라서 k=6일 때 부등식을 만족하므로 정답은 6이다.
17. 확률변수 X가 이항분포 B(150, 3/5) 을 따를 때, 다음 표준정규 분포표를 이용하여 확률 P(81 ≤ X ≤ 96) 을 구하면?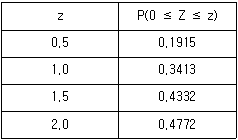
- 0.5328
- 0.6247
- 0.7745
- 0.8185
- 이항분포의 평균과 분산은 각각 np = 150 × 3/5 = 90, np(1-p) = 150 × 3/5 × 2/5 = 36 이다. 따라서 이항분포를 표준정규분포로 근사시키기 위해 표준화를 해야 한다.
Z = (X - μ) / σ = (X - 90) / √36 = (X - 90) / 6
따라서 P(81 ≤ X ≤ 96) 은 P((81-90)/6 ≤ Z ≤ (96-90)/6) = P(-1.5 ≤ Z ≤ 1) 이다.
이때, 표준정규분포표에서 -1.5에 해당하는 확률은 0.0668이고, 1에 해당하는 확률은 0.8413이다.
따라서 P(-1.5 ≤ Z ≤ 1) = 0.8413 - 0.0668 = 0.7745 이다.
따라서 정답은 "0.7745"이다.
18. 두 실수 x, y가 (x-2i)+y(1+xi)=4 를 만족할 때, x3+y3의 값은? (단, i=√-1)
- 40
- 42
- 44
- 46
- (x-2i)+y(1+xi)=4 에서 복소수의 실수부와 허수부를 각각 비교해보면,
x-y^2=4 (1)
-2xy=0
-2xy=0 에서 x=0 또는 y=0 이다.
만약 x=0 이면, (1) 식에 대입하면 y=±2 이다.
만약 y=0 이면, (1) 식에 대입하면 x=4 이다.
따라서 가능한 경우는 (0,2), (0,-2), (4,0) 이다.
이제 각 경우에 대해 x^3+y^3 을 계산해보면,
(0,2) : 0+8=8
(0,-2) : 0+(-8)=-8
(4,0) : 64+0=64
따라서 정답은 40이다.
19. 함수 f(x)=2x2-3x+5 에 대하여, 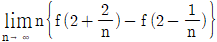 의 값은?
의 값은?
- 6
- 9
- 12
- 15
- 주어진 식에 x=2를 대입하여 계산하면 f(2)=2(2)2-3(2)+5=8-6+5=7 이다. 따라서 보기 중에서 f(2)의 값이 15인 보기는 없으므로 정답은 없다.






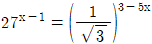 의 해는?
의 해는?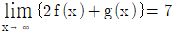 ,
, 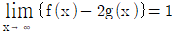 일 때,
일 때, 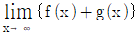 의 값은?
의 값은?
= log3(6^2)-log3(2^(1/2))^4
= log36^2-2log32^2
= 2log36-4log32
= 2(log36-2log32)
= 2(log36-log32^2)
= 2(log36-log34)
= 2log3(6/4)
= 2log3(3/2)
= 2
따라서 정답은 "2"이다.