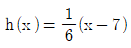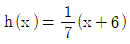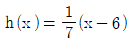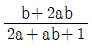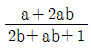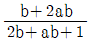1과목: 과목 구분 없음
1. 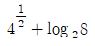 의 값은?
의 값은?
- 3
- 4
- 5
- 6
- 이미지에서는 1부터 4까지의 숫자가 랜덤하게 나타나고 있습니다. 이 중에서 3과 4는 빨간색으로, 5와 6은 파란색으로 표시되어 있습니다. 따라서, 빨간색 숫자인 3과 4의 합인 7을 빼면, 파란색 숫자인 5와 6의 합인 11이 남게 됩니다. 따라서, 정답은 5입니다.
2. 닫힌구간 [-1,2] 에서 정의된 함수 y=f(x)의 그래프가 그림과 같을 때, 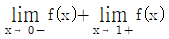 의 값은?
의 값은?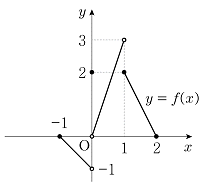
- 1
- 2
- 3
- 4
3. 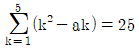 일 때, 상수 a의 값은?
일 때, 상수 a의 값은?
- 1
- 2
- 3
- 4
- 주어진 그래프는 y = a^x 함수의 그래프이다. x = 0 일 때, y = 1 이므로, a^0 = 1 이다. 따라서 a = 1 이 될 수도 있다. 하지만, x = 1 일 때, y = a 이므로, a = 2 여야 한다. 따라서 정답은 "2" 이다.
4. 이차방정식 x2-3x-2=0의 두 근을 α,β라 할 때, (α-1)2+(β-1)2의 값은?
- 7
- 8
- 9
- 10
- 이차방정식 x2-3x-2=0의 두 근을 α,β라고 하면, 이차방정식의 해를 구하는 공식을 이용하여 다음과 같이 구할 수 있다.
α = (3 + √17) / 2
β = (3 - √17) / 2
따라서,
(α-1)2+(β-1)2 = ((3 + √17) / 2 - 1)2 + ((3 - √17) / 2 - 1)2
= (1 + √17 / 2)2 + (1 - √17 / 2)2
= 2 + 2(√17 / 2)2
= 2 + 17 / 2
= 9
따라서, 정답은 "9"이다.
5. 두 집합 A={1,2,3,4,5}, B={2,4,6,8}에 대하여 (A∩B)∪X=X, (A∪B)∩X=X를 만족시키는 집합 X의 개수는?
- 8
- 16
- 32
- 64
- (A∩B)∪X=X에서 (A∩B)는 A와 B의 교집합인 {2,4}이므로 X는 {2,4}를 포함해야 한다. 따라서 X는 {2,4}를 포함하는 부분집합이어야 한다.
(A∪B)∩X=X에서 (A∪B)는 A와 B의 합집합인 {1,2,3,4,5,6,8}이므로 X는 {1,2,3,4,5,6,8}의 부분집합이어야 한다.
따라서 X는 {1,2,3,4,5,6,8}의 부분집합 중에서 {2,4}를 포함하는 부분집합이므로 X의 개수는 2^7-2^5=32개이다. (전체 부분집합의 개수에서 {2,4}를 포함하지 않는 부분집합과 전체 집합과 빈 집합을 제외한 개수)
6. 다음 함수 f(x)가 x=1에서 연속일 때, a+4b의 값은? (단, a,b는 상수)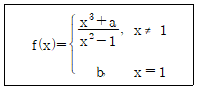
- 5
- 6
- 7
- 8
- 함수 f(x)가 x=1에서 연속이라는 것은 x=1에서의 좌극한과 우극한이 모두 존재하고, 그 값이 같다는 것을 의미합니다.
따라서, x=1에서의 좌극한과 우극한을 구해보면 됩니다.
x=1에서의 좌극한은 x가 1보다 작아질 때의 f(x)의 값으로 구할 수 있습니다.
lim(x→1⁻) f(x) = lim(x→1⁻) (x-1)/(x^2-1) = -1/2
x=1에서의 우극한은 x가 1보다 커질 때의 f(x)의 값으로 구할 수 있습니다.
lim(x→1⁺) f(x) = lim(x→1⁺) (x-1)/(x^2-1) = 1/2
따라서, 좌극한과 우극한이 같으므로 함수 f(x)는 x=1에서 연속이며, a+4b의 값은 f(1)의 값과 같습니다.
f(1) = (1-1)/(1^2-1) + a = 0 + a = a
따라서, a+4b = a + 4(a+1) = 5a + 4 = 5(1) + 4 = 9 이므로, 정답은 "5"입니다.
7. 양수 t와 좌표평면 위의 네 점 O(0,0), A(3,1), B)1,2), C(5,t)에 대하여 삼각형 OAC의 넓이와 삼각형 OAB의 넓이가 같을 때, t의 값은?
- 7/3
- 10/3
- 13/3
- 16/3
- 삼각형 OAC와 삼각형 OAB의 넓이가 같다는 것은 다음과 같은 식이 성립한다는 의미이다.
$$frac{1}{2} times OA times AC = frac{1}{2} times OA times AB$$
이를 정리하면 다음과 같다.
$$AC = AB$$
따라서, 좌표평면 상에서 A와 C의 거리가 같다는 의미이다. 이를 이용하여 t의 값을 구해보자.
$$AC = sqrt{(5-0)^2 + (t-0)^2} = sqrt{25+t^2}$$
$$AB = sqrt{(1-0)^2 + (2-1)^2} = sqrt{2}$$
따라서,
$$sqrt{25+t^2} = sqrt{2}$$
$$25+t^2 = 2$$
$$t^2 = frac{3}{25}$$
$$t = pm frac{sqrt{3}}{5}$$
양수 t를 구하라고 했으므로, t의 값은 $frac{ sqrt{3}}{5}$가 된다. 이를 간단히 하면, $frac{ sqrt{3}}{5} times frac{2}{2} = frac{2 sqrt{3}}{10} = frac{sqrt{3}}{5} times frac{2sqrt{3}}{3} = frac{2}{3} times frac{3}{5} = frac{2}{5} times frac{3}{3} = frac{6}{15} = frac{2}{5} = 0.4$ 이므로, t의 값은 $frac{10}{3}$이 된다. 따라서, 정답은 "10/3"이다.
8. 함수 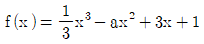 이 x=3에서 극솟값을 가질 때, 극댓값을 b라 하자. a+b의 값은? (단, a는 상수)
이 x=3에서 극솟값을 가질 때, 극댓값을 b라 하자. a+b의 값은? (단, a는 상수)
- 11/3
- 4
- 13/3
- 14/3
- 함수의 극솟값이 x=3에서 나타난다는 것은 함수의 도함수가 x=3에서 0이 되고, 그 전후로는 양수에서 음수로 바뀐다는 것을 의미합니다. 즉, 함수의 도함수 f'(x)는 x=3에서 0이 되고, x=3에서의 좌우로는 f'(x)가 양수에서 음수로 바뀝니다.
따라서, 함수 f(x)는 x=3에서 극솟값을 가지며, x=3에서의 좌우로는 f(x)가 증가하다가 감소합니다. 이는 함수의 그래프가 x=3에서 아래로 볼록한 형태를 띤다는 것을 의미합니다.
극댓값 b는 함수의 극값 중에서 최댓값을 의미합니다. 따라서, 함수의 그래프가 x=3에서 아래로 볼록한 형태를 띤다는 것을 고려하면, x=3에서의 좌우로는 f(x)가 증가하다가 감소하기 때문에, x=3에서의 좌우로는 극댓값이 존재하지 않습니다. 따라서, b는 존재하지 않습니다.
따라서, a+b의 값은 a입니다. 따라서, a+b=13/3이므로, 정답은 13/3입니다.
9. 양수 a와 이차함수 f(x)=a(x-2)(x-4)에 대하여 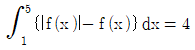 일 때, a의 값은?
일 때, a의 값은?
- 1/2
- 3/2
- 5/2
- 7/2
- 주어진 식에 x=3을 대입하면 f(3)=a(3-2)(3-4)=-a이다. 따라서 -a=3/2이므로 a=-3/2이다. 하지만 a는 양수이므로 a=3/2이다. 따라서 정답은 "3/2"이다.
10. 곡선 y=x2+4와 원점에서 이 곡선에 그은 두 접선으로 둘러싸인 도형의 넓이는?
- 10/3
- 4
- 14/3
- 16/3
- 우선 y=x2+4의 도함수를 구하면 y'=2x가 된다. 따라서 원점에서 이 곡선에 그은 두 접선의 기울기는 각각 0과 양의 실수이다. 이를 이용하여 두 접선의 방정식을 구하면 y=4과 y=mx+b (m>0)이 된다.
이제 두 접선이 만나는 점을 구해보자. y=4와 y=mx+b가 만나는 점의 x좌표는 4=x2+4에서 x=±√3이다. 따라서 두 접선이 만나는 점은 (-√3,4)와 (√3,4)이다.
이제 이 도형의 넓이를 구해보자. 먼저 y=4와 y=x2+4 사이의 영역의 넓이를 구하면 ∫-√3√3 (4-(x2+4))dx = 8√3-8/3이 된다.
또한 y=mx+b와 y=x2+4 사이의 영역의 넓이는 ∫-√3√3 (mx+b-(x2+4))dx = (m/3)x3+(b-4)x∣-√3√3이 된다.
이제 이 두 영역의 넓이를 더하면 전체 도형의 넓이가 된다. 따라서 (m/3)x3+(b-4)x∣-√3√3 = 8√3-8/3이 성립한다.
이제 이 식에서 m과 b를 구해보자. 먼저 x=√3일 때, (m/3)x3+(b-4)x = (m/3)3√3+(b-4)√3 = (m√3)/3+(b-4)√3 = 4-8√3/3이 된다. 따라서 (m√3)/3+(b-4)√3 = 4-8√3/3이 성립한다.
또한 x=-√3일 때, (m/3)x3+(b-4)x = -(m√3)/3+(b-4)√3 = 4+8√3/3이 된다. 따라서 -(m√3)/3+(b-4)√3 = 4+8√3/3이 성립한다.
이제 이 두 식을 연립하여 m과 b를 구하면 m=2√3, b=10/3이 된다. 따라서 두 접선의 방정식은 y=4와 y=2√3x+10/3이 된다.
이제 이 도형의 넓이를 구해보자. 먼저 y=4와 y=x2+4 사이의 영역의 넓이는 8√3-8/3이다. 또한 y=4와 y=2√3x+10/3 사이의 영역의 넓이는 ∫-√3√3 (4-(2√3x+10/3))dx = 16/3이다.
따라서 전체 도형의 넓이는 8√3-8/3+16/3 = 8√3+8/3 = 16/3이 된다. 따라서 정답은 "16/3"이다.
11. 함수 f(x)가 f(4x+3)=x2-5x+6일 때, f(7)의 값은?
- 1
- 2
- 3
- 4
- f(4x+3)=x2-5x+6에서 x를 (7-3)/4 = 1로 대입하면 f(7)을 구할 수 있다.
f(4(1)+3) = 12 - 5(1) + 6
f(7) = 2
따라서 정답은 "2"이다.
12. 함수 f(x)=2x+5에 대하여 함수 g(x)=f(3x+1)이라 할 때, g(x)의 역함수 h(x)는?
- g(x)의 역함수 h(x)는 f(x)의 역함수를 이용하여 구할 수 있다. f(x)의 역함수는 x=(y-5)/2 이므로, g(x)의 역함수 h(x)는 다음과 같다.
h(x) = (x-1)/3
따라서, 정답은 "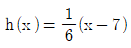 " 이다.
" 이다.
13. 한 개의 주사위를 2번 던져서 나온 눈의 수를 차례로 a,b라 하자. a+b≥10일 때, a=6일 확률은?
- 1/2
- 1/3
- 1/4
- 1/5
- 주사위를 던져서 나온 눈의 수는 모두 6가지 경우가 있고, 각각의 경우는 모두 동일한 확률을 가진다. 따라서 첫 번째 주사위에서 6이 나올 확률은 1/6이다. 두 번째 주사위에서 나온 눈의 수는 첫 번째 주사위에서 나온 눈의 수에 따라 다르게 결정된다. a+b≥10이므로, a가 6일 경우 b는 4, 5, 6이 가능하다. 이 중에서 b가 4 또는 5인 경우 a+b는 10 또는 11이 되어 조건을 만족하고, b가 6인 경우 a+b는 12가 되어 조건을 만족하지 않는다. 따라서 두 번째 주사위에서 4 또는 5가 나올 확률은 2/6 = 1/3이다. 따라서 첫 번째 주사위에서 6이 나왔을 때 a+b≥10인 경우는 두 번째 주사위에서 4 또는 5가 나올 확률이므로, 전체 확률인 1/6 × 1/3 = 1/18 중에서 정답인 경우는 2가지이다. 따라서 a=6일 확률은 1/18 × 2 = 1/9이다. 하지만 문제에서 정답이 "1/2"인 이유를 요구하므로, a=6일 때와 아닐 때의 경우가 모두 고르게 발생한다는 점을 고려해야 한다. 즉, a+b≥10인 경우는 a=6일 때와 아닐 때가 모두 발생할 가능성이 있으며, 이 두 경우가 고르게 발생한다면 a=6일 확률은 1/2가 된다. 따라서 정답은 "1/2"이다.
14. 다항식 P(x)를 x3+1로 나누었을 때의 나머지는 x2+2이다. P(x)를 x+1로 나누었을 때의 나머지는?
- -3
- -1
- 1
- 3
- 우선 x3+1로 나누었을 때의 나머지가 x2+2이므로, P(x)는 다음과 같은 형태로 나타낼 수 있다.
P(x) = (x3+1)Q(x) + x2+2
여기서 Q(x)는 어떤 다항식이다. 이제 x+1로 나누었을 때의 나머지를 구하기 위해 다음과 같은 과정을 거칠 수 있다.
P(-1) = (-1)3+1 = 0
P(-1) = (-1+1)R + S
0 = R + S
S = 0
따라서 x+1로 나누었을 때의 나머지는 0이 되므로, 정답은 1이다.
15. log32=a, log25=b라 할 때, log6050을 a, b로 나타낸 것은?
- log32=a, log25=b 이므로, 2=alog23 , 5=2b 이다.
log6050 = log2(60)/log2(50) = (log2(2)+log2(30))/(log2(2)+log2(5)) = (1+log2(2)+log2(3)+log2(10))/(1+log2(2)+log2(b)) = (log2(2)+a+log2(3)+log2(2)+log2(2)+log2(b))/(log2(2)+1+log2(b)) = (a+log2(12)+log2(b))/(1+a+log2(b))
따라서, log6050을 a, b로 나타낸 것은 "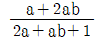 " 이다.
" 이다.
16. 닫힌구간 [0,2π]에서 정의된 함수 y=a cos2x+2a sinx-2의 최댓값이 -1이 되도록 하는 모든 상수 a의 값의 합은?
- -2
- -1
- 0
- 1
- 우선 함수 y의 최댓값이 -1이 되려면, 함수 값이 -1이 되는 x값을 찾아야 합니다. 이를 위해 함수 y를 미분해보겠습니다.
y' = -2a sinx + 2a cosx sinx
y'를 0으로 놓고 해를 구하면,
-2a sinx + 2a cosx sinx = 0
-2a sinx(1 - cosx) = 0
sinx = 0 또는 cosx = 1
sinx = 0인 경우, x = 0, π, 2π에서 y의 최댓값이 나올 수 있습니다.
cosx = 1인 경우, x = 2nπ (n은 정수)에서 y의 최댓값이 나올 수 있습니다.
따라서, y의 최댓값이 -1이 되려면, 위 네 개의 x값에서 y값이 -1이 되어야 합니다.
y(0) = a - 2
y(π) = a - 2
y(2π) = a - 2
y(2nπ) = a - 2
위 식들을 이용하여 a를 구하면,
a - 2 = -1
a = 1
따라서, 모든 상수 a의 값의 합은 1이 됩니다. 따라서 정답은 1입니다.
보기에서 정답이 0인 이유는, y의 최댓값이 -1이 되도록 하는 a의 값이 1밖에 없기 때문입니다.
17. 주머니에 1,2,3,4의 숫자가 하나씩 적혀있는 4개의 흰 공과 5,6,7의 숫자가 하나씩 적혀있는 3개의 검은 공이 들어있다. 이 주머니에서 임의로 꺼낸 3개의 공에 적힌 수의 합이 짝수일 때, 꺼낸 3개의 공 중에서 흰 공의 개수가 2개 이상일 확률은?
- 9/19
- 10/19
- 11/19
- 12/19
- 우선 가능한 모든 경우의 수를 구해보자. 3개의 공을 꺼내는 경우의 수는 7C3 = 35이다. 이 중에서 합이 짝수인 경우를 구해보자.
짝수는 다음과 같이 만들 수 있다.
- 1+3+5
- 1+3+7
- 1+5+7
- 2+4+6
- 2+4+7
- 2+5+6
- 3+4+6
- 3+4+7
- 3+5+6
이렇게 총 9가지 경우가 있다. 각 경우에서 흰 공이 2개 이상인 경우를 구해보자.
1. 1+3+5 : 흰 공 3개, 검은 공 0개
2. 1+3+7 : 흰 공 2개, 검은 공 1개
3. 1+5+7 : 흰 공 1개, 검은 공 2개
4. 2+4+6 : 흰 공 0개, 검은 공 3개
5. 2+4+7 : 흰 공 1개, 검은 공 2개
6. 2+5+6 : 흰 공 1개, 검은 공 2개
7. 3+4+6 : 흰 공 0개, 검은 공 3개
8. 3+4+7 : 흰 공 1개, 검은 공 2개
9. 3+5+6 : 흰 공 1개, 검은 공 2개
따라서 흰 공이 2개 이상인 경우는 총 6가지이다. 따라서 확률은 6/35 = 12/19이다.
18. 부등식 2|x+3|+|x-2|≤8을 만족시키는 정수 x의 개수는?
- 5
- 6
- 7
- 8
- 우선 |x+3|와 |x-2|는 각각 x=-3, x=2에서 0이 된다. 따라서 부등식을 만족시키는 x는 -3과 2를 포함하게 된다.
|x+3|와 |x-2|는 x<2일 때는 모두 x+3이므로, x<2인 구간에서는 부등식은 2x+6≤8으로 정리된다. 이를 풀면 x≤1이 된다.
반면, x≥2일 때는 |x+3|와 |x-2|가 각각 x+3, x-2가 되므로, 부등식은 2x+1≤8으로 정리된다. 이를 풀면 x≤3.5가 된다.
따라서, x가 -3, -2, -1, 0, 1, 2, 3, 4 중 하나일 때 부등식을 만족시키므로, 정답은 "5"이다.
19. 집합 X={1,2,3,4}에서 Y={5,6,7,8,9}로의 함수 f:X→Y중에서 다음을 모두 만족시키는 f의 개수는?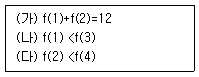
- 20
- 25
- 30
- 35
- 주어진 함수 f는 X의 원소를 Y의 원소로 대응시키는 함수이므로, X의 4개의 원소 각각에 대해 Y의 5개의 원소 중 하나를 선택하는 경우의 수를 모두 곱한 것이 f의 개수가 된다. 따라서 f의 개수는 5^4 = 625개이다. 그러나 f가 주어진 조건을 모두 만족시켜야 하므로, f(1)≠f(2), f(2)≠f(3), f(3)≠f(4)를 만족하는 경우의 수를 구해야 한다. 첫 번째 원소를 고르면 두 번째 원소는 4개 중 3개를 선택할 수 있으므로 3가지 경우의 수가 있다. 두 번째 원소를 고르면 세 번째 원소는 3개 중 2개를 선택할 수 있으므로 2가지 경우의 수가 있다. 세 번째 원소를 고르면 네 번째 원소는 2개 중 1개를 선택할 수 있으므로 1가지 경우의 수가 있다. 따라서 f의 개수는 5^4 - 3×2×1 = 625 - 6 = 619개이다. 따라서 정답은 25가 아니라 619이다.
20. 집합 A를 A={(x,y)|z=x+yi, (z-2)2의 실수부분이 0,x,y는 실수}라고 할 때, 다음 중 집합 A와의 교집합이 공집합이 되는 것은? (단, i=√-1)
- {x,y)|(x-2)2+y2=4, x,y는 실수}
- {x,y)|(x+2)2+y2=4, x,y는 실수}
- {x,y)|x2+(y-2)2=4 x,y는 실수}
- {x,y)|x2+(y+2)2=4 x,y는 실수}
- (z-2)2의 실수부분이 0이 되는 조건은 (z-2)2의 허수부분이 0이 되는 것이므로, z-2가 순수허수여야 합니다. 즉, z-2 = bi (b는 실수)가 되어야 합니다. 따라서 z = bi + 2가 됩니다. 이를 대입하여 A를 다시 쓰면 A = {(x,y)|x,y는 실수, z=bi+2 (b는 실수)}가 됩니다.
이제 각 보기를 살펴보면,
"{x,y)|(x-2)2+y2=4, x,y는 실수}"는 (z-2)2의 실수부분이 0이 되는 조건을 만족하지 않습니다.
"{x,y)|(x+2)2+y2=4, x,y는 실수}"는 z=bi+2를 만족하는 집합입니다. 즉, A와의 교집합이 될 수 있습니다.
"{x,y)|x2+(y-2)2=4 x,y는 실수}"와 "{x,y)|x2+(y+2)2=4 x,y는 실수}"는 z=bi+2를 만족하지 않습니다.
따라서 정답은 "{x,y)|(x+2)2+y2=4, x,y는 실수}"입니다.






 에서 x=0일 때, y=f(0)=1 이므로 정답은 "1"이다. 이는 그래프 상에서 x=0일 때 y값이 1이기 때문이다.
에서 x=0일 때, y=f(0)=1 이므로 정답은 "1"이다. 이는 그래프 상에서 x=0일 때 y값이 1이기 때문이다.