1과목: 과목 구분 없음
1. 그림과 같은 하중이 작용할 때 지점 A에 대한 휨모멘트[kNㆍm]는?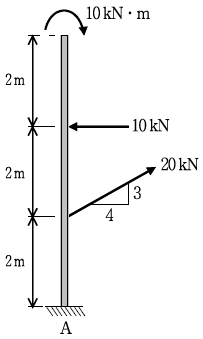
- 2
- 4
- 8
- 10
2. 단면의 성질에 대한 설명으로 옳지 않은 것은?
- x축, y축에 대한 단면 1차 모멘트는 Qx=∑aiyi, Qy=∑aixi 이며, (면적×거리)의 합이므로 단위는 ㎣, m3등으로 표시한다.
- x축, y축에 대한 단면 2차 모멘트는 Ix=∑aiyi2, Iy=∑aixi2 으로 항상 (+)값을 가지며, (면적×거리2)의 합이므로 단위는 mm4, m4등으로 표시한다.
- 단면 1차 모멘트는 좌표축에 따라 (+), (-)의 부호를 가지며 도심을 지나는 축에 대하여 최대이다.
- 단면계수(section modulus)는 단면 2차 모멘트를 도심축으로부터 최상단 또는 최하단까지의 거리로 나눈 값으로 단위는 ㎣, m3등으로 표시한다.
3. 그림과 같이 정삼각형 구조체에 힘이 작용하고 있을 때 평형을 이루기 위해 필요한 모멘트[kNㆍm]는?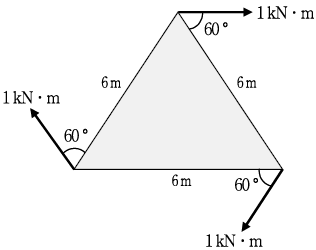
- 3 (시계방향)
- 4√3 (반시계방향)
- 6 (반시계방향)
- 6√3 (반시계방향)
4. 힘의 평형에 대한 설명 중 옳지 않은 것은?
- 2차원 평면상에서 한 점에 작용하는 힘들의 평형조건은 2개이다.
- 3차원 공간상에서 한 물체에 작용하는 힘들의 평형조건은 4개이다.
- 3차원 공간상에서 한 점에 작용하는 힘들의 평형조건은 3개이다.
- 2차원 평면상에서 한 물체에 작용하는 힘들의 평형조건은 3개이다.
5. 그림과 같이 길이가 200 mm이고, 단면이 20 mm × 20 mm인 강봉에 60 kN의 축방향 인장력이 작용하여 강봉이 0.15 mm 늘어났을 때 이 강봉의 탄성계수[MPa]는?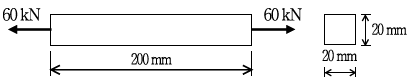
- 2.0 × 105
- 2.0 × 104
- 8.0 × 105
- 8.0 × 104
6. 외적으로 정정인 구조물에 대한 설명으로 옳지 않은 것은?
- 구하고자 하는 반력의 갯수와 평형 방정식의 갯수가 같다.
- 외부 온도의 변화에 의해 추가적인 반력이 발생하지 않는다.
- 동일한 외부하중에서 구조물 부재들의 강성이 달라지면 반력이 달라진다.
- 구조물 제작오차에 의해 추가적인 반력이 발생하지 않는다.
7. 그림과 같이 무응력 상태로 봉 AB부재와 봉 BC부재가 연결되어 있다. 만일, 봉 AB부재의 온도가 T만큼 상승했을 때 봉 BC부재에 응력이 생기지 않기 위해 봉 BC부재에 필요한 온도 변화량은? (단, 봉 AB부재와 봉 BC부재 사이는 길이를 무시할 수 있는 단열재에 의해 열의 이동이 완전히 차단되어 있다고 가정한다)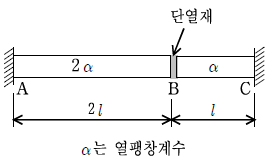
- 2T(하강)
- 2T(상승)
- 4T(하강)
- 4T(상승)
8. 그림과 같이 절점 D는 내부 힌지로 연결되어 있으며, 점 A에 수평하중 P가 작용하고 비신장 케이블 FG부재로 무게 W를 지지하는 게르버보(Gerber Beam)가 있다. 이때 지점 C에서 수직반력이 발생하지 않도록 하기 위한 하중 P에 대한 무게 W의 비는?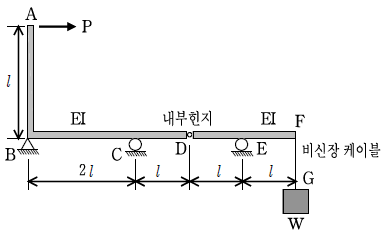
- W/P = 1/2
- W/P = 1/3
- W/P = 3
- W/P = 1
9. 다음 설명 중 옳지 않은 것은?
- 일정한 속력으로 직선 운동하는 물체의 가속도는 영(zero)이다.
- 일정한 속력으로 곡선 운동하는 물체의 가속도는 영(zero)이 아니다.
- 구조물의 단면에 휨모멘트가 작용하면 연직응력이 발생하지만 전단응력은 발생하지 않는다.
- 물 속에 잠긴 물체의 표면에 작용하는 압력은 물체 표면에 항상 수직으로 작용한다.
10. 그림과 같이 트러스의 C점에 하중 P=8 kN이 작용한다면 AB부재가 받는 힘[kN]은?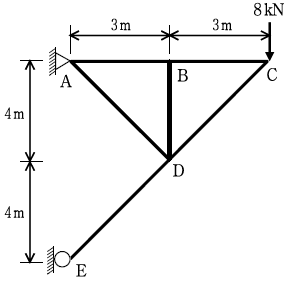
- 4(압축)
- 4(인장)
- 6(압축)
- 6(인장)
11. 그림과 같은 라멘 구조물의 부정정 차수는?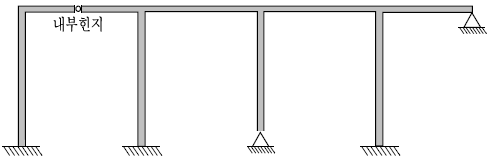
- 7차
- 8차
- 9차
- 10차
12. 그림과 같은 트러스는 불안정 구조물로 판별되었다. 안정 구조물로 변환하기 위한 방법으로 옳지 않은 것은?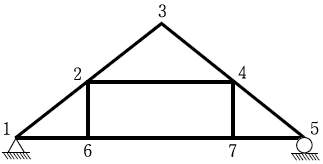
- 2번 절점과 7번 절점을 연결하는 부재 추가
- 5번 지점을 힌지로 교체
- 4번 절점과 6번 절점을 연결하는 부재 추가
- 1번 지점을 이동단으로 교체
13. 그림과 같은 구조물에서 지점 A의 수평반력 HA[kN], 수직반력 RA[kN] 및 휨모멘트 MA[kNㆍm]는?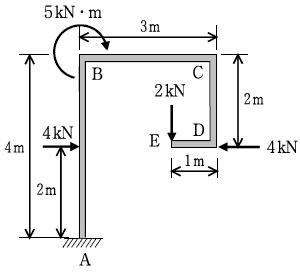
- HA: 2, RA: 2, MA: 5
- HA: 2, RA: 2, MA: 9
- HA: 0, RA: 2, MA: 5
- HA: 0, RA: 2, MA: 9
14. 그림과 같은 단순보에 모멘트 하중이 작용할 때의 설명으로 옳지 않은 것은?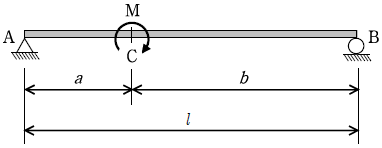
- 전단력의 크기는 AB구간 전체에서 일정하다.
- 휨모멘트는 C단면에서 부호가 바뀌게 된다.
- 축방향력은 모멘트 하중의 작용위치에 상관없이 영(zero)이다.
- 지점 A와 지점 B의 반력의 크기는 모멘트 하중의 작용위치에 따라 달라진다.
15. 그림과 같은 직사각형 단주가 있다. 이 단주의 상단 A점에 압축력 24 kN이 작용할 때, 단주의 하단에 발생하는 최대 압축응력 [MPa]은?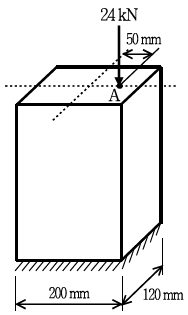
- 1.5
- 1.75
- 2.0
- 2.5
16. 그림과 같이 집중하중과 등분포하중이 동시에 작용하는 단순보에서 구간 AB의 휨모멘트 분포식으로 옳은 것은? (단, 휨모멘트 단위는 kNㆍm로 한다)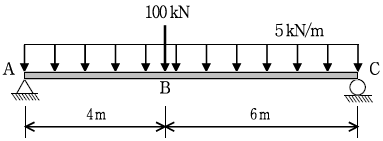
- -2.5x2+85x
- 2.5x2+85x
- -2.5x2+45x
- 2.5x2+45x
17. 그림과 같은 캔틸레버보(Cantilever Beam)에서 B점의 처짐각(θB)은?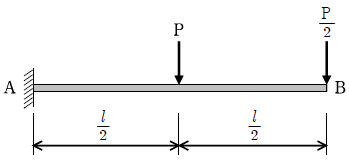
- 3Pl2/8EI
- 3Pl2/16EI
- 5Pl2/24EI
- 5Pl2/27EI
18. 그림과 같은 단순보 구조물에서 전단력이 영(zero)이 되는 구간의 길이와 최대 휨모멘트는?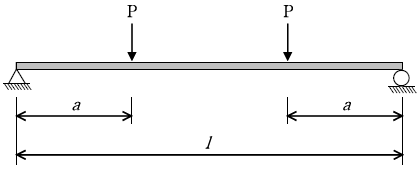
- 2 a , Pa
- 2 a , P (l -2 a)
- l -2 a , Pa
- l -2 a , P (l -2 a)
19. 그림과 같이 집중하중과 등분포하중이 동시에 작용할 때, 단순보 내부에서 발생하는 응력에 대한 설명으로 옳지 않은 것은?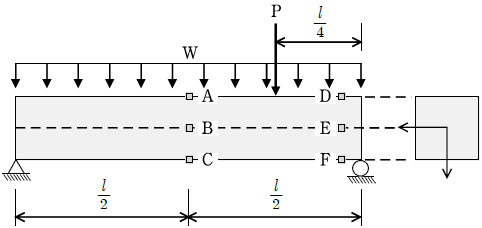
- 단순보 전구간에서 최대 휨인장응력은 C점에서 발생한다.
- E점에서 휨응력은 영(zero)이다.
- B점에서는 전단응력만 발생한다.
- A점에서는 휨압축응력이 발생한다.
20. 그림과 같은 보 구조물에서 지점 B의 수직반력[kN]은?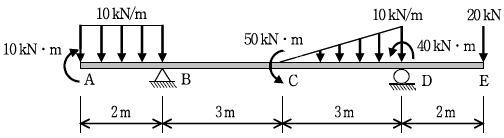
- 30.0
- 32.5
- 35.0
- 37.5






이유는 지점 A에서의 힘의 합력선이 A 지점에서의 지지력과 일치하기 때문입니다. 따라서 A 지점에서의 휨모멘트는 0이 됩니다.
만약 합력선이 A 지점에서 지지력과 일치하지 않는다면, A 지점에서의 힘의 합력선과 지지력의 합력선이 만나는 지점에서의 휨모멘트를 계산해야 합니다.