1과목: 과목 구분 없음
1. 그림과 같이 P1=13kN, P2=7√2kN의 힘이 O점에 작용할 때, A점에 대한 모멘트의 크기[kN⋅m]는?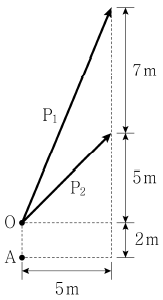
- 24
- 26
- 28
- 30
2. 그림과 같은 게르버보에 대한 설명으로 옳지 않은 것은? (단, 구조물의 자중은 무시한다)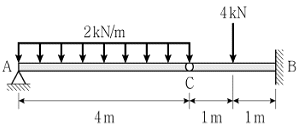
- A점에서 수직반력의 크기는 4 kN이다.
- B점에서 수직반력의 크기는 8 kN이다.
- C점에서 전단력의 크기는 4 kN이다.
- B점에서 휨모멘트반력의 크기는 16 kN⋅m이다.
3. 그림과 같이 내부 힌지를 가지고 있는 게르버보에서 B점의 정성적인 휨모멘트의 영향선은?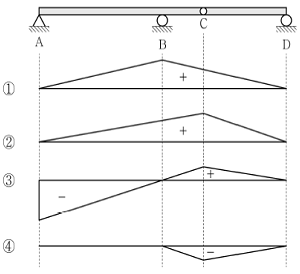
- ①
- ②
- ③
- ④
4. 그림과 같이 도형의 도심 C의 축에 대한 탄성단면계수의 크기가 큰 것부터 바르게 나열한 것은?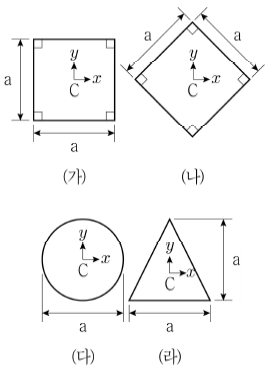
- (가) > (나) > (다) > (라)
- (나) > (가) > (다) > (라)
- (가) > (나) > (라) > (다)
- (나) > (가) > (라) > (다)
5. 그림과 같이 압축력 P를 받는 길이가 L인 강체봉이 A점은 회전스프링(스프링 계수 kθ)으로, B점은 병진스프링(스프링 계수 k)으로 각각 지지되어 있다. 좌굴하중 Pcr의 크기는? (단, 봉의 자중은 무시하고, 미소변형이론을 적용한다)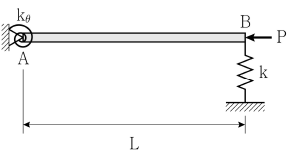
- kL + kθ/2L
- kL + kθ/L
- 2kL + kθ/L
- 2kL + kθ/2L
6. 그림과 같이 길이가 L인 단순보에 삼각형 분포하중이 작용하고 있다. A점과 B점의 수직반력이 같다면, 삼각형 분포하중이 작용하는 거리 x는? (단, 구조물의 자중은 무시한다)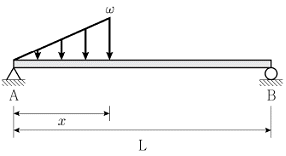
- 0.25L
- 0.5L
- 0.75L
- 1.0L
7. 그림과 같이 집중하중을 받는 케이블로 구성된 구조물에서 힌지 지점 A에서 수평반력의 크기[kN]는? (단, 구조물의 자중은 무시한다)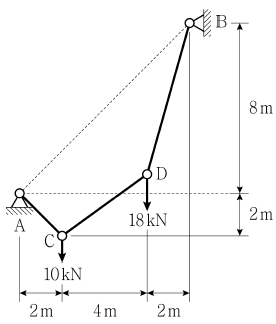
- 6
- 8
- 10
- 12
8. 그림과 같은 구조물에서 스프링을 제외한 봉의 온도가 30°C만큼 전 단면에서 균일하게 상승할 때, 늘어난 봉의 길이[mm]는? (단, 봉의 열팽창계수 α=10-5/°C, 탄성계수 E=200 GPa, 단면적 A=100 mm2이고, 스프링 계수 k=2,000 N/mm이며, 구조물의 좌굴 및 자중은 무시한다)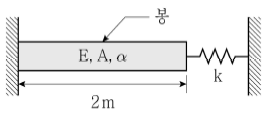
- 0.2
- 0.3
- 0.4
- 0.5
9. 그림과 같이 평면에 변형률 로제트 게이지를 부착하여 3방향의 변형률 εA, εB, εC를 측정하였을 때, 최대전단변형률 γmax의 크기 [10-6]는? (단, εA=250 × 10-6, εB=130 × 10-6, εC=235 × 10-6이다)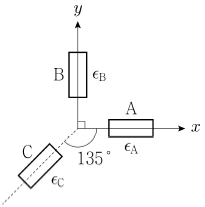
- 100
- 150
- 200
- 250
10. 그림과 같은 부정정 구조물의 A점에 처짐각 θA=0.025 rad이 발생하였다. 이때 A점에 작용하는 휨모멘트 MA의 크기[N⋅mm]는? (단, 휨강성 EI=40,000N⋅mm2이며, 구조물의 자중은 무시한다)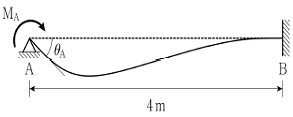
- 0.5
- 1.0
- 5.0
- 10.0
11. 그림과 같이 길이 L인 캔틸레버보의 끝에 집중하중 P가 작용할 때 휨에 의한 변형에너지의 크기는  이다. 상수 C1의 크기는? (단, 전단변형에 의한 에너지는 무시하고, 휨강성 EI는 일정하며, 구조물의 자중은 무시한다)
이다. 상수 C1의 크기는? (단, 전단변형에 의한 에너지는 무시하고, 휨강성 EI는 일정하며, 구조물의 자중은 무시한다)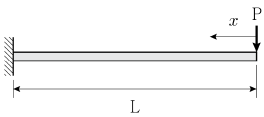
- 1/3
- 1/4
- 1/6
- 1/12
12. 그림과 같이 내부 힌지가 있는 보에서 C점의 수직반력은? (단, 구조물의 자중은 무시한다)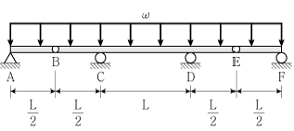
- (6/5)ωL
- (5/4)ωL
- (4/3)ωL
- (3/2)ωL
13. 그림과 같은 단순보에 집중하중 P와 분포하중 ω=P/L 가 작용할 경우, A점의 처짐각은  이다. 상수 C1의 크기는? (단, 보의 휨강성 EI는 일정하고, 구조물의 자중은 무시한다)
이다. 상수 C1의 크기는? (단, 보의 휨강성 EI는 일정하고, 구조물의 자중은 무시한다)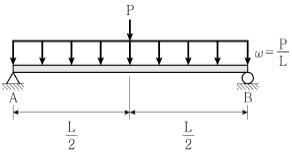
- 5/48
- 7/48
- 7/24
- 11/24
14. 그림과 같은 보 (가), (나), (다)의 부정정 차수를 모두 합한 차수는?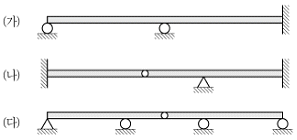
- 5차
- 6차
- 7차
- 8차
15. 그림과 같은 평면응력요소에서 최대전단응력 τmax과 최대주응력 σmax의 크기[MPa]는?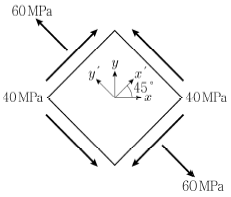
- τmax: 10, σmax: 40
- τmax: 10, σmax: 60
- τmax: 50, σmax: 80
- τmax: 50, σmax: 110
16. 그림과 같은 보에서 A점의 휨모멘트반력 MA의 크기[kN⋅m]는? (단, 휨강성 EI는 일정하고, 구조물의 자중은 무시한다)
- 20
- 44
- 52
- 60
17. 그림과 같이 평면 역계에서 자중 W=550 kN인 물체에 도르래를 이용하여 힘 P=250 kN이 작용한다. 물체가 평형상태를 유지하기 위한 물체와 바닥 사이의 최소정지마찰계수의 크기는? (단, 도르래와 케이블 사이의 마찰력은 무시한다)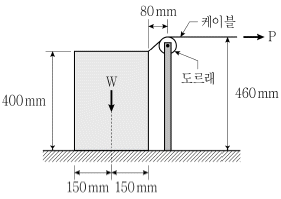
- 3/10
- 4/11
- 1/2
- 7/11
18. 그림과 같은 트러스 구조물에서 부재 AB의 부재력 크기[kN]는? (단, 구조물의 자중은 무시한다)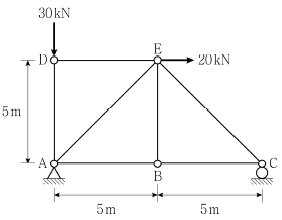
- 10
- 10√2
- 50
- 50√2
19. 그림과 같은 내민보에서 휨모멘트가 0이 되는 위치까지의 수평거리 x로 옳은 것은? (단, 구조물의 자중은 무시한다)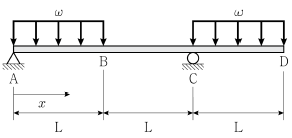
- 0.7 L
- 1.0 L
- 1.2 L
- 1.5 L
20. 그림과 같이 등분포하중이 작용하는 선형탄성재료의 캔틸레버보에서 처짐공식을 사용하여 구한 C점의 처짐은 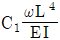 이다. 상수 C1의 크기는? (단, 등분포하중 ω가 캔틸레버보 길이 L의 전 구간에 작용할 때, 자유단에서 처짐각
이다. 상수 C1의 크기는? (단, 등분포하중 ω가 캔틸레버보 길이 L의 전 구간에 작용할 때, 자유단에서 처짐각 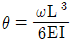 , 처짐
, 처짐 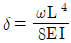 이고, 휨강성 EI는 일정하며, 구조물의 자중은 무시한다)
이고, 휨강성 EI는 일정하며, 구조물의 자중은 무시한다)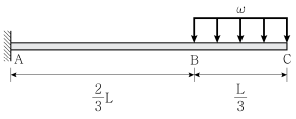
- 4/81
- 41/384
- 49/648
- 163/1944






먼저 P1의 힘 벡터와 A점 사이의 거리를 구해보겠습니다. 삼각형 OAP에서 OA = 3, OP1 = 5, AP1 = 4√2 이므로, AO = √(OA² - OP1²) = √(9 - 25) = √16 = 4입니다.
따라서 P1에 대한 모멘트는 13 × 4 = 52kN⋅m입니다.
다음으로 P2의 힘 벡터와 A점 사이의 거리를 구해보겠습니다. 삼각형 OAB에서 OA = 3, OB = 3, AB = 3√2 이므로, AO = BO = √(OA² - OB²) = √(9 - 9) = 0, AB = 3√2입니다.
따라서 P2에 대한 모멘트는 7√2 × 3√2 = 42kN⋅m입니다.
따라서 A점에 대한 모멘트의 크기는 52 + 42 = 94kN⋅m입니다.
하지만 문제에서는 정답을 2의 배수로 제시하고 있으므로, 가장 가까운 2의 배수인 24가 정답이 됩니다.