1과목: 과목 구분 없음
1. 전단탄성계수 G에 대한 설명으로 옳은 것은? (단, 포아송비 ν는 이다)
- 탄성계수 E보다 크고, 포아송비 ν가 커짐에 따라 증가한다.
- 탄성계수 E보다 작고, 포아송비 ν가 커짐에 따라 증가한다.
- 탄성계수 E보다 크고, 포아송비 ν가 커짐에 따라 감소한다.
- 탄성계수 E보다 작고, 포아송비 ν가 커짐에 따라 감소한다.
2. 그림과 같이 크기가 같고 방향이 반대인 우력이 작용할 때, 옳지 않은 설명은? (단, a, b, c는 0보다 큰 상수이다)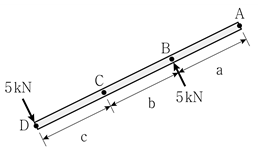
- A점 C점의 모멘트의 크기가 같다.
- B점 D점의 모멘트의 방향이 같다.
- A점 D점의 모멘트의 크기와 방향이 모두 같다.
- B점 C점의 모멘트의 크기는 다르나 방향은 같다.
3. 그림과 같이 음영으로 표시된 도형에서 도심까지의 거리 y0는?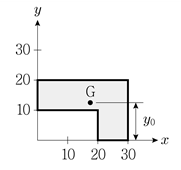
- 11.5
- 12.5
- 13.5
- 14.5
4. 다음은 부정정 라멘 구조물이다. 부정정 차수가 다른 하나는?
5. 그림과 같은 단면적이 동일한 3개의 단면에 대하여 도심축(X축)에 대한 단면2차모멘트의 크기 순서로 옳게 표현된 것은?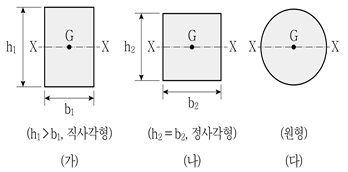
- (가)>(다)>(나)
- (가)>(나)>(다)
- (나)>(다)>(가)
- (나)>(가)>(다)
6. 길이 L인 단순보에 대하여, 부재 중앙에 수직집중하중 P가 작용할 때의 최대휨모멘트(Mmax(p))와 수직등분포하중 w가 전체 보에 작용할 때의 최대휨모멘트(Mmax(w))가 같다면, 등분포하중 w의 크기는?
- P/2L
- P/L
- 2P/L
- 3P/L
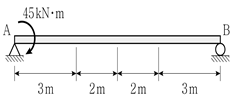
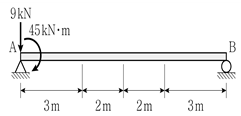
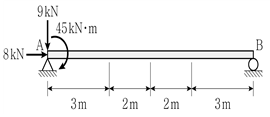
7. 그림과 같이 단순보에 하중이 작용할 때, A점에 작용하는 등가의 힘-우력계로 옳게 나타낸 것은?
8. 그림과 같은 하중을 받는 트러스 구조물에서 부재 AB의 부재력[kN]은? (단, 부재의 축강성 EA는 일정하고, 구조물의 자중은 무시한다)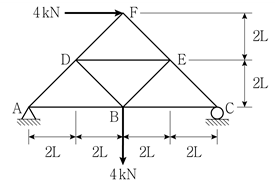
- 0
- 2√2(압축)
- 4(압축)
- 4(인장)
9. 그림은 단순보의 전단력도(S.F.D.)를 나타낸 것이다. 단순보에 발생하는 최대휨모멘트의 크기[kNㆍm]는?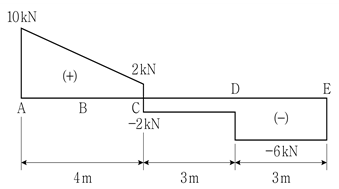
- 18
- 20
- 24
- 30
10. 그림과 같이 단순보에 3각형 분포하중과 집중하중이 작용하고 있다. 두 지지점의 수직반력(RA, RB)이 같다면, 집중하중 P의 크기[kN]는? (단, 보의 자중은 무시한다)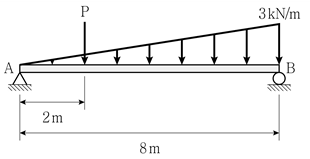
- 4
- 6
- 8
- 9
11. 그림과 같은 평면응력 상태(σx=-60MPa, σy=-20MPa)일 때, 최대전단응력의 크기(τmax)는?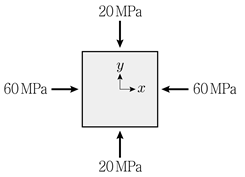
- 10MPa
- 20MPa
- 30MPa
- 40MPa
12. 그림과 같이 단면 폭 100mm, 높이가 200mm의 직사각형 단면을 갖는 단순보가 있다. 허용휨응력(σa)이 60MPa이고, 허용전단응력(τa)이 1MPa이라면, 허용휨응력을 적용시킨 최대집중하중(Pmax(σx))과 허용전단응력을 적용시킨 최대집중하중(Pmax(τx))과의 비(Pmax(σx) : Pmax(τx))는? (단, 선형탄성이론을 적용하고, 휨강성 EI는 일정하며, 구조물의 자중은 무시한다)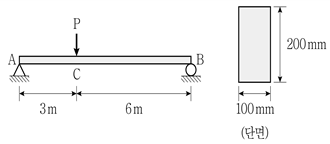
- 1:1
- 2:1
- 3:1
- 4:1
13. 그림과 같은 캔틸레버보에 집중하중 P와 집중모멘트 M이 작용할 때, A점에 발생하는 처짐의 크기는? (단, 보의 휨강성 EI는 일정하고, 보의 자중은 무시한다)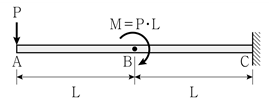
14. 그림과 같이 축강성(EA)이 일정한 트러스 구조물에 수직하중 P가 작용하고 있다. 부재 BD와 부재 CD의 부재력의 비(FBD/FCD)는? (단, 미소변형이론을 적용하고, 구조물의 자중은 무시한다)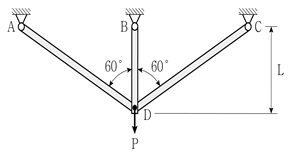
- 4
- 2
- 2√3
- 1/√3
15. 그림 (가)와 같은 양단이 핀 지지된 길이 5m 기둥의 오일러 좌굴하중(Pcr)의 크기가 160kN일 때, 그림 (나)와 같은 양단 고정된 길이 4m 기둥의 오일러 좌굴하중의 크기[kN]는? (단, 두 기둥의 단면은 동일하고, 탄성계수는 같으며, 구조물의 자중은 무시한다)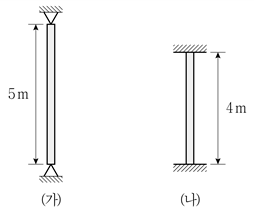
- 200
- 250
- 800
- 1,000
16. 그림과 같이 B점에 내부힌지가 있는 게르버보에서 C점에서의 휨모멘트의 영향선으로 옳은 것은?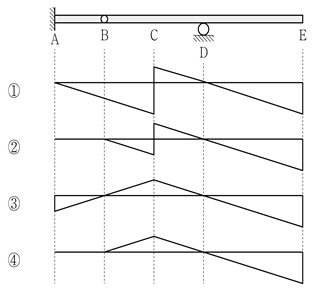
- ①
- ②
- ③
- ④
17. 그림과 같이 집중하중 P가 작용하는 단순보에서, 지지점 B에서 θ=60° 경사면에 반력 RB가 작용한다. 지지점 B에서 반력 RB의 크기[kN]는? (단, 보의 자중은 무시한다)
- 40.0
- 37.5
- 35.0
- 30.0
18. 그림과 같이 단면 폭 300mm, 높이가 400mm의 직사각형 단면을 갖는 단순보가 있다. 이 단순보가 축방향으로 120kN의 인장력을 받고, 수직하중 20kN을 받을 때, 보 중앙(C점)의 단면 최상부에 발생하는 응력의 크기[MPa]는? (단, 보의 자중은 무시한다)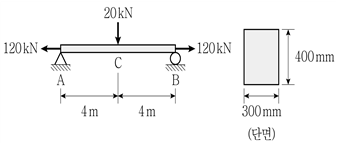
- 4(압축)
- 4(인장)
- 2(압축)
- 2(인장)
19. 그림과 같이 구조물의 C점에 하중 P가 작용하여 지지점 B의 지점침하가 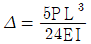 만큼 발생하였다. 이때 B점에서 발생하는 반력 RB와 C점에서 작용하는 하중 P의 비
만큼 발생하였다. 이때 B점에서 발생하는 반력 RB와 C점에서 작용하는 하중 P의 비 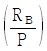 는? (단, 보의 휨강성 EI는 일정하고, 보의 자중은 무시한다)
는? (단, 보의 휨강성 EI는 일정하고, 보의 자중은 무시한다)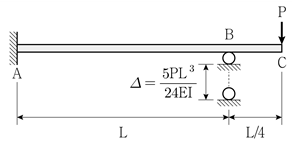
- 1/2
- 2/3
- 3/4
- 5/6
20. 직사각형 단면을 가지는 보에 휨모멘트가 작용하여 그림 (가)와 같이 단면에 응력분포가 발생하였다. 보의 재료는 그림 (나)와 같이 완전탄소성거동을 한다고 가정하였을 때, 보의 단면에 발생하는 최대변형률의 크기는? (단, 그림 (나)는 압축과 인장에서 동일하게 적용되며, 항복응력(σy)은 200MPa, 탄성계수(E)는 200GPa이다)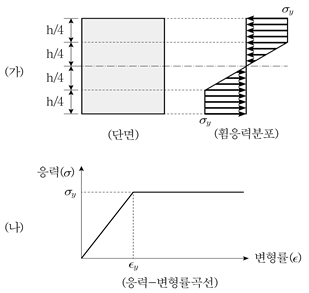
- 0.0025
- 0.0020
- 0.0015
- 0.0010







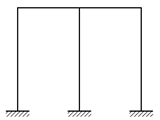
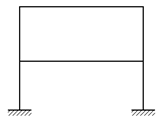
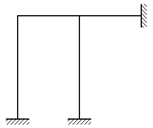
 "이다. 이유는 부정정 라멘 구조물에서 차수란 라멘 구조물 내에서 한 원자가 결합한 다른 원자의 수를 의미한다. "
"이다. 이유는 부정정 라멘 구조물에서 차수란 라멘 구조물 내에서 한 원자가 결합한 다른 원자의 수를 의미한다. "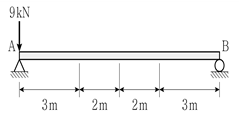
 "이 정답이다. "
"이 정답이다. " "은 하중의 크기와 방향이 반대인 힘이고, "
"은 하중의 크기와 방향이 반대인 힘이고, " "은 보의 수직방향 반작용력이 아니라 수평방향 반작용력이다. "
"은 보의 수직방향 반작용력이 아니라 수평방향 반작용력이다. " "는 A점에 작용하는 힘이 아니다.
"는 A점에 작용하는 힘이 아니다.


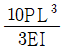
 "이다.
"이다.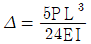 만큼 발생했을 때, C점에서의 지점침하는
만큼 발생했을 때, C점에서의 지점침하는 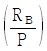 =
=
전단탄성계수 G는 고체가 변형될 때 전단응력과 전단변형률 사이의 비율을 나타내는 지표이다. 탄성계수 E는 고체가 변형될 때 축방향 응력과 축방향 변형률 사이의 비율을 나타내는 지표이다.
포아송비 ν는 고체가 축방향으로 변형될 때, 이에 수반되는 전단변형률과 수평방향으로의 변형률 사이의 비율을 나타내는 지표이다.
전단탄성계수 G는 탄성계수 E보다 작은 값이며, 포아송비 ν가 커짐에 따라 감소한다. 이는 포아송비 ν가 커짐에 따라 축방향 변형률이 증가하면서 전단응력이 감소하기 때문이다.