1과목: 과목 구분 없음
1. 다음 설명은 2015년 도로교설계기준(한계상태설계법)에서 규정하는 어떤 한계상태에 대한 것인가?
- 사용한계상태
- 피로와 파단한계상태
- 극한한계상태
- 극단상황한계상태
2. 사용하중이 작용하여 인장측 콘크리트에 휨인장균열이 발생한 단철근 직사각형 보에서 압축연단의 콘크리트 응력이 10MPa일 때 인장철근의 응력[MPa]은? (단, 재료는 Hooke의 법칙이 성립하고, 단면의 유효깊이 d=450mm, 압축연단에서 중립축까지의 거리 c=150mm, 철근의 탄성계수 Es=210GPa, 콘크리트의 탄성계수 Ec=30,000MPa이다)
- 100
- 120
- 140
- 160
3. 그림과 같은 T형보를 직사각형보로 해석할 수 있는 최대 철근량 As[mm2]는? (단, fck=20MPa, fy=400MPa이며 2012년도 콘크리트구조기준을 적용한다)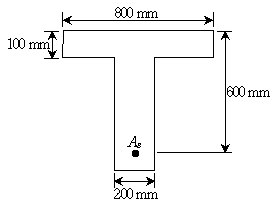
- 3,400
- 1,700
- 340
- 170
4. 그림과 같은 필릿용접부의 전단응력[MPa]은?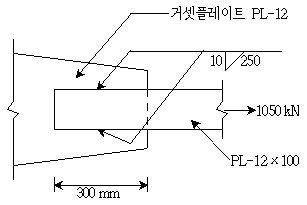
- 250
- 300
- 325
- 350
5. 정모멘트를 받는 보의 최소 인장 철근량에 대한 설명으로 옳지 않은 것은? (단, fck는 콘크리트의 설계기준압축강도, fy는 철근의 설계기준항복강도, bw는 복부의 폭, d는 단면의 유효깊이이며, 2012년도 콘크리트구조기준을 적용한다)
- 부재의 모든 단면에서 해석에 의해 필요한 철근량보다 1/3 이상 인장철근이 더 배치되는 경우는 최소철근량 규정을 적용하지 않을 수 있다.
- 부재의 최소철근량은
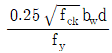 와
와 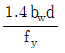 중 큰 값 이상으로 한다.
중 큰 값 이상으로 한다. - 인장측 균열의 발생과 동시에 갑작스럽게 파괴되는 것을 방지하기 위해서 최소철근량을 규정한다.
- 철근의 항복과 콘크리트의 극한변형률 도달이 동시에 발생하도록 하기 위해 최소철근량을 규정한다.
6. 한 변의 길이가 300mm인 정사각형 단면을 가진 철근콘크리트 기둥에 편심이 없는 단기하중이 축방향으로 작용하고 있다. 축방향 철근의 단면적 Ast=2,500mm2, 철근의 탄성계수 Es=200 GPa, 콘크리트의 탄성계수 Ec=25GPa일 때 철근이 받는 응력이 120MPa이라면 콘크리트가 받는 응력[MPa]은? (단, 콘크리트의 설계기준압축강도 fck=40MPa이며, 철근과 콘크리트 모두 탄성범위 이내에서 거동한다)
- 10
- 12
- 15
- 18
7. 단철근 직사각형보에서 콘크리트의 설계기준압축강도 fck=25MPa, 철근의 설계기준항복강도 fy=300MPa, 철근의 탄성계수 Es=200GPa, 단면의 유효깊이 d=450mm일 때 균형단면이 되기 위한 압축연단으로부터 중립축까지의 거리[mm]는? (단, 2012년도 콘크리트구조기준을 적용한다)
- 200
- 250
- 300
- 350
8. 휨 및 압축을 받는 콘크리트 부재의 설계가정에 대한 설명으로 옳지 않은 것은? (단, 2012년도 콘크리트구조기준을 적용한다)
- 휨모멘트 또는 휨모멘트와 축력을 동시에 받는 부재의 콘크리트 압축 연단의 극한변형률은 0.003으로 가정한다.
- 철근의 응력이 설계기준항복강도 fy 이하일 때 철근의 응력은 변형률에 탄성계수를 곱한 값으로 하고, 철근의 변형률이 fy에 대응하는 변형률보다 큰 경우 철근의 응력은 철근의 극한강도까지 증가시킨다.
- 깊은보는 비선형 변형률 분포를 고려하여 설계하여야 한다. 그러나 비선형 분포를 고려하는 대신 스트럿-타이 모델을 적용할 수도 있다.
- 콘크리트 압축응력의 분포와 콘크리트 변형률 사이의 관계는 직사각형, 사다리꼴, 포물선형 또는 실험의 결과와 실질적으로 일치하는 형상으로도 가정할 수 있다.
9. 지름 d=600mm인 철근콘크리트 원형단면 기둥을 단주로 볼 수 있는 최대 높이[m]는? (단, 압축부재의 유효좌굴길이계수 k=1.5, 비횡구속 골조이며, 2012년도 콘크리트구조기준을 적용한다)
- 2.2
- 2.5
- 3.6
- 4.5
10. 그림과 같은 지간 L=10m의 단순보에 자중을 포함한 등분포 계수하중 wu=60kN/m가 작용하는 경우, 전단위험단면에서 전단철근이 부담해야 할 설계전단력 øVs[kN]는? (단, 보통중량콘크리트로서 fck=25MPa이며, 2012년도 콘크리트구조기준을 적용한다)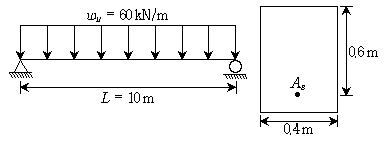
- 114
- 135
- 152
- 186
11. 유효프리스트레스 fpe를 결정하기 위하여 고려해야 하는 프리스트레스손실 원인을 모두 고른 것은?
- ㄱ, ㄴ, ㄹ
- ㄱ, ㄷ, ㄹ, ㅁ
- ㄱ, ㄴ, ㄷ, ㅁ
- ㄴ, ㄷ, ㄹ, ㅁ
12. 그림과 같이 편심이 없는 하중 T를 받는 볼트로 연결된 판이 ABFGHIJ로 파괴되기 위한 p[mm]의 범위는? (단, 연결재 구멍의 직경은 20mm이다)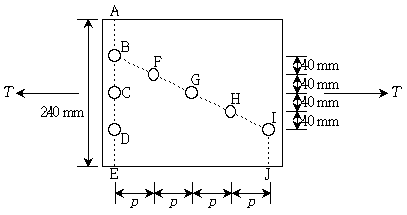
- 30≤p<40
- 40≤p<50
- 70≤p<80
- 80≤p<100
13. 하중저항계수설계법을 적용한 강구조설계기준(2014)에서 기술하고 있는 강도저항계수에 대한 설명으로 옳지 않은 것은?
- 인장재의 총단면의 항복에 대한 강도저항계수 øt=0.90을 적용한다.
- 인장재의 유효순단면의 파괴에 대한 강도저항계수 øt=0.85를 적용한다.
- 중심축 압축력을 받는 압축부재의 강도저항계수 øc=0.90을 적용한다.
- 비틀림이 발생하지 않은 휨부재의 강도저항계수 øb=0.90을 적용한다.
14. 복철근 콘크리트보의 탄성처짐이 10mm일 경우, 5년 이상의 지속하중에 의해 유발되는 추가 장기처짐량[mm]은? (단, 보의 압축철근비는 0.02이며, 2012년도 콘크리트구조기준을 적용한다)
- 2.5
- 5.0
- 7.5
- 10.0
15. 프리스트레스트콘크리트 휨부재는 미리 압축을 가한 인장구역에서 사용하중에 의한 인장연단응력 ft에 따라 균열등급을 구분한다. 비균열등급에 속하는 인장연단응력 ft[MPa]는? (단, fck는 콘크리트 설계기준압축강도이며, 2012년도 콘크리트구조기준을 적용한다)
16. 철근콘크리트 부재의 전단철근에 대한 설명으로 옳지 않은 것은? (단, λ는 경량콘크리트계수, fck는 콘크리트 설계기준압축강도, bw는 복부의 폭, d는 단면의 유효깊이, Vs는 전단철근에 의한 단면의 공칭전단강도이며, 2012년도 콘크리트구조기준을 적용한다)
- 최소 전단철근은 경사균열폭이 확대되는 것을 억제함으로써 덜 취성적인 파괴를 유도한다.
- 부재축에 직각으로 배치된 전단철근의 간격은 Vs가
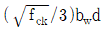 이하인 경우 d/2 이하이어야 하고, 또한 600mm 이하로 하여야 한다.
이하인 경우 d/2 이하이어야 하고, 또한 600mm 이하로 하여야 한다. - Vs가
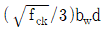 을 초과하는 경우 Vs가
을 초과하는 경우 Vs가 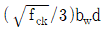 이하일 때 적용된 최대 간격을 절반으로 감소시켜야 한다.
이하일 때 적용된 최대 간격을 절반으로 감소시켜야 한다. - 경사스터럽과 굽힘철근은 부재의 중간 높이인 0.5d에서 보의 지간 중간 방향으로 주인장 철근까지 연장된 45°선과 한 번 이상 수직으로 교차되도록 배치하여야 한다.
17. 그림과 같이 정사각형 확대 기초에 기둥의 자중을 포함한 고정하중 D=3,000kN과 활하중 L=2,700kN이 편심이 없이 기초판에 작용할 때 확대 기초 한 변의 최소 길이 ℓ[m]은? (단, 기초 지반의 허용지지력 qa=240kN/m2, 철근콘크리트 단위중량 γc=24kN/m3, 토사 무게는 무시하며, 2012년도 콘크리트구조기준을 적용한다)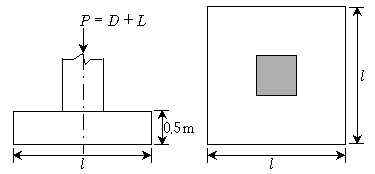
- 4
- 5
- 6
- 7
18. 연속보 또는 1방향 슬래브는 구조해석을 정확하게 하는 대신 콘크리트구조기준(2012)에 따라 근사해법을 적용하여 약산할 수 있다. 근사해법을 적용하기 위한 조건으로 옳지 않은 것은?
- 활하중이 고정하중의 3배를 초과하지 않는 경우
- 부재의 단면이 일정하고, 2경간 이상인 경우
- 인접 2경간의 차이가 짧은 경간의 30% 이하인 경우
- 등분포 하중이 작용하는 경우
19. 그림과 같은 프리스트레스트콘크리트 단순보에 프리스트레스힘 P=4,800kN, 자중을 포함한 등분포하중 w=80kN/m가 작용할 경우 지간 중앙단면의 하연응력[MPa]은? (단, 지간 중앙의 긴장재의 편심 e=0.4m이며 프리스트레스손실은 없다고 가정한다)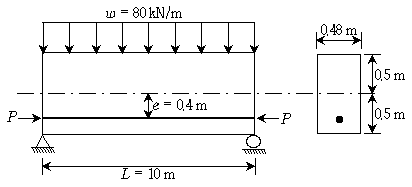
- 20.5(인장응력)
- 21.5(압축응력)
- 22.5(인장응력)
- 23.5(압축응력)
20. 철근의 정착 및 이음에 대한 설명으로 옳은 것은? (단, ldb는 정착길이, db는 철근의 직경, fck는 콘크리트의 설계기준압축강도, fy는 철근의 설계기준항복강도, 2012년도 콘크리트구조기준을 적용한다)
- 갈고리에 의한 정착은 압축철근의 정착에 유효하다.
- 3개의 철근으로 구성된 다발철근의 정착길이는 개개 철근의 정착길이보다 33% 증가시켜야 한다.
- 보통중량콘크리트에서 인장 이형철근의 기본정착길이는
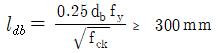 이다.
이다. - D35를 초과하는 철근끼리는 인장부에서 겹침이음을 할 수 없다.






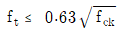

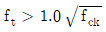
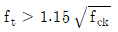
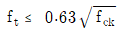 "이다.
"이다.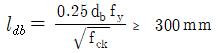 이다."입니다.
이다."입니다.