1과목: 과목 구분 없음
1. 두 개의 물체 A, B가 수평면 에서 줄에 매달려 각각 등속 원운동을 하고 있다. 물체 A에 의한 원 궤적 반지름은 물체 B에 의한 원 궤적 반지름의 절반이고, 물체 A가 원을 한 바퀴 도는 데 걸리는 시간은 물체 B가 원을 한 바퀴 도는 데 걸리는 시간의 2배이다. 물체 A의 속력을 vA, 물체 B의 속력을 vB라 할 때, vB/vA의 값은?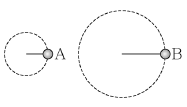
- 1/2
- 2
- 4
- 8
2. 그림처럼 용수철 상수가 k1=1000N/m, k2=500N/m인 두 개의 용수철이 수직으로 연결되어 있다. 여기에 질량 1kg인 물체를 매달았을 때 두 용수철이 늘어난 총 길이는? (단, 중력 가속도 g=10m/s2로 한다.)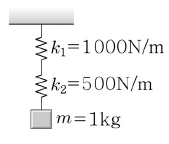
- 1/1.5cm
- 1.5cm
- 1/3cm
- 3cm
3. 지구 주위를 도는 위성의 궤도 운동에 대한 아래 설명 중 가장 옳은 것은? (단, 위성의 궤도 운동은 지구 중심을 중심으로 하는 등속 원운동이라 가정한다.)
- 궤도 운동 주기는 궤도 반지름에 반비례한다.
- 궤도 운동 주기는 위성 질량과 무관하다.
- 같은 주기로 도는 위성의 각운동량은 위성 질량에 무관하다.
- 궤도 운동하는 위성의 총 역학적 에너지 값은 양수이다.
4. 그림은 매질 A에서 같은 경로로 입사하여 매질 B를 지나 거울에서 반사한 빨간색 빛과 파란색 빛의 경로를 나타낸 것이다. B에서 두 빛에 대한 매질의 굴절률은 n으로 같다. A와 B의 경계면은 거울 면과 나란하다. <보기>에서 이에 대한 설명으로 옳은 것을 모두 고른 것은?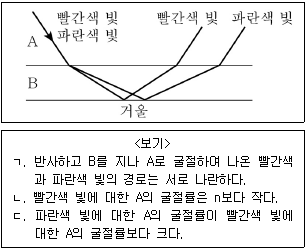
- ㄱ
- ㄴ
- ㄱ, ㄷ
- ㄱ, ㄴ, ㄷ
5. 그림과 같은 U모양의 관에 밀도가 p인 액체 a를 채우고 관의 한 쪽에 액체 b를 높이 10cm만큼 채웠더니 액체 윗면의 높이차가 3cm가 되었다. b의 밀도는?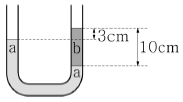
- 3/10p
- 3/7p
- 3/5p
- 7/10p
6. 위치 A에서 초기 속력이 0인 상태의 물체가 움직이기 시작하여 위치 B와 C를 지날 때 물체의 속력이 각각 vB, vC라고 하자. v2B/v2C의 값은? (단, 마찰은 무시한다.)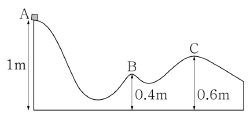
- 3/2
- 9/4
- 2/3
- 4/9
7. 그림과 같이 마찰이 없는 평면상에서 질량이 같은 두 물체가 각각 수평방향으로 2v, 수직방향으로 v의 초기속도로 진행하다 충돌하여 하나로 뭉쳐져 계속 진행한다. 충돌 후 두 물체의 총 역학적 에너지는 충돌 전 총 역학적 에너지의 몇 배인가?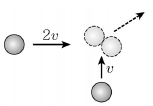
- 0.1배
- 0.5배
- 1배
- 2배
8. 그림처럼 지름이 10cm에서 5cm로 줄어드는 관이 있다. 지름이 큰 부분인 단면적 A에서 유입되는 유체의 속력이 20cm/s였다면, 줄어든 단면적 B에서 유체의 속력은? (단, 유체는 정상흐름을 하고 있다.)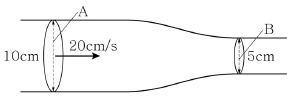
- 80cm/s
- 40cm/s
- 10cm/s
- 5cm/s
9. 두 개의 컵에 서로 다른 유체 A, B가 담겨 있다. 각각의 컵에 동일한 재질로 만든 같은 크기의 균일한 물체를 넣었을 때 유체 A, B에 잠긴 정도가 달랐다. 유체 A에는 물체의 절반이 잠겼고, 유체 B에는 물체의 3/4 이 잠긴 상태에서 평형을 유지하고 있다. 유체 A, B의 밀도를 pA, pB라고 할 때 pA/pB 의 값은?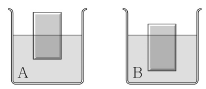
- 3/2
- 4/3
- 5/4
- 6/5
10. 높이 80m 되는 폭포에서 물이 떨어질 때 중력에 의한 위치 에너지의 감소가 모두 물의 내부 에너지로 변화 하였다면 폭포 바닥에 떨어진 물의 온도 변화는? (단, 중력 가속도g=10m/s2=10N/kg, 물의 비열 c=4kJ/kg·K로 한다.)
- 20K
- 5K
- 0.5K
- 0.2K
11. 1몰의 이상기체가 열역학적 평형 상태 A1에서 열역학적 평형 상태 A2로 변하였다. 각 상태 Ai에서의 온도, 압력, 부피는 Ti, Pi, Vi로 표시되며, T1=T2, P1>P2, V1<V2였다. 열역학적 평형 상태 A1에서 A2로의 변화 과정에 대한 설명 중 가장 옳은 것은?
- 기체가 외부로 열을 방출한다.
- 기체가 외부에서 열을 흡수한다.
- 기체의 내부 에너지는 증가한다.
- 기체의 내부 에너지는 감소한다.
12. 그림 (가)와 같이 q, 3q의 전하가 거리 d만큼 떨어져 정지해 있을 때 두 전하 사이의 힘의 크기는 F이다. 그림 (나)와 같이 2q, Q의 전하가 거리 2d만큼 떨어져 있을 때 두 전하 사이의 힘의 크기는 2F이다. Q의 크기는?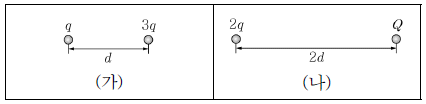
- 4q
- 6q
- 8q
- 12q
13. 극판의 면적이 A이고 간격이 d인 평행판 축전기에 전하 q가 대전되어 있을 때, 축전기에 에너지가 저장되며 단위 부피당 에너지 밀도는 u1이다. 극판의 간격을 2d로 늘리고 대전된 전하를 2q로 만들었을 때의 에너지 밀도를 u2라고 하면, u2/u1의 값은?
- 1
- 2
- 4
- 8
14. 축전기와 유도기가 직렬로 연결된 LC회로가 있다. 이 회로에 동일한 축전기와 유도기를 각각 추가로 직렬 연결하여 얻어지는 LC회로의 각진동수는 원래 LC회로 각진동수의 몇 배가 되는가?
- 1배
- 1/√2배
- 1/2배
- 1/4배
15. 가정용 스피커의 최대 일률은 스피커 1m 앞에서 1kHz의 진동수를 가지는 음파로 측정한다. 어떤 스피커의 최대 일률이 60W였다면 음파의 세기는? (단, 스피커는 점원에서 전면으로만 균일하게 반구 형태로 소리를 방출하며, 편의를 위해 π=3으로 계산한다.)
- 60W/m2
- 30W/m2
- 10W/m2
- 5W/m2
16. 그림과 같이 평평한 바닥에서 초기 속력이 2m/s인 물체가 용수철 판에 부딪친다. 용수철은 10cm만큼 압축되었다가 제자리로 돌아오고 이 순간 물체는 용수철 판에서 튕겨 나온다. 용수철이 압축되는 구간의 바닥면은 운동마찰계수가 μk=0.5이고 다른 바닥면은 마찰이 없다. 물체가 용수철 판에서 튕겨 나오는 순간의 속력은? (단, 중력 가속도 g=10m/s2로 한다.)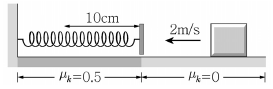
- 4m/s
- 2m/s
- √2m/s
- 1m/s
17. 유도기, 저항, 기전력원, 스위치를 그림과 같이 연결하여 회로를 구성한 후 스위치를 닫아 회로에 전류가 흐르기 시작했다. 스위치를 닫은 후 충분히 오랜 시간이 지나 일정한 크기의 전류가 회로에 흐르게 되었을 때, 유도기에 저장된 에너지는? (단, 인덕턴스(inductance), 저항, 기전력의 크기는 L, R, V0이다.)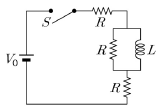
18. 겹실틈[double-slit] 간섭 실험에서 실틈 사이의 거리가 d0, 간섭 실험에 사용된 빛의 파장이 λ0일 때 밝은 간섭 무늬 사이의 거리는 일정하고 그 값은 y0이다. 실틈 사이의 거리를2d0, 빛의 파장을 2λ0로 바꿨을 때 밝은 간섭 무늬 사이의 거리가 일정한 경우 그 거리의 값은?
- y0/2
- y0
- 2y0
- 3y0
19. <표>는 여러 반도체와 절연체의 띠틈을 나타낸 것이다. ⓐ와 ⓑ는 각각 반도체와 절연체 중 하나이고, ⓒ와 ⓓ는 각각 다이아몬드와 실리콘 중 하나이다. <보기> 에서 옳은 설명을 모두 고른 것은?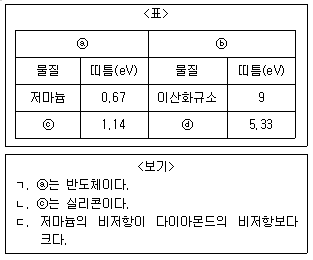
- ㄱ
- ㄱ, ㄴ
- ㄷ
- ㄴ, ㄷ
20. 전자의 운동 에너지가 100eV일 때, 물질파 파장이 λ0이다. 전자의 운동 에너지가 400eV일 때 물질파 파장은?
- λ0/8
- λ0/4
- λ0/2
- λ0






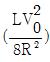
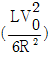
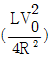
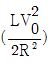
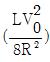 "이다.
"이다.
또한, 물체 A와 B의 반지름의 관계는 rA = 2rB 이다.
속력은 반지름과 주기의 관계로 v = 2πr/T 이므로,
vA = 2πrA/TA = 2π(2rB)/(TB/2) = 4πrB/TB = 4vB
따라서, vB/vA = 1/4 이므로 정답은 "4"이다.