1과목: 과목 구분 없음
1. <보기>는 일직선 상에서, 0초일 때 1m/s의 속력으로 운동하는 물체의 가속도를 시간에 따라 나타낸 것이다. 이 물체의 운동에 대한 설명으로 가장 옳은 것은? (단, 0초일 때 물체의 운동 방향을 (+)로 한다.)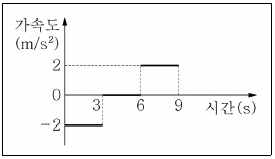
- 0~9초 동안 운동 방향은 바뀌지 않았다.
- 4초일 때의 속력은 5m/s 이다.
- 0~9초 사이에 0초일 때의 위치로부터 변위의 크기는 9초일 때가 가장 크다.
- 0초부터 3초까지 처음과 같은 방향으로 6m 이동한다.
2. 두 위성 A, B가 행성을 중심으로 등속원운동을 하고 있다. 행성 중심으로부터 A, B 중심까지의 거리는 각각 2r, 3r이다. A와 B의 가속도 크기를 각각 aA, aB라 하고, 공전주기를 각각 TA, TB라고 할 때, aA : aB와 TA : TB를 옳게 짝지은 것은? (단, A와 B에는 행성에 의한 만유인력만 작용한다.)
- ①
- ②
- ③
- ④
3. <보기>와 같이 직육면체 금속의 세 변의 길이의 비가 a:b:c=1:2:3 이다. 10V의 전원을 A와 B단자(양옆면)에 걸었을 때, 소비전력을 PAB라 하고, 같은 전원을 C와 D단자(위, 아래면)에 걸었을 때 소비전력을 PCD 라 할 때, PAB:PCD값은? (단, 두 단자는 금속 내에 균일한 전류를 형성하게 한다.)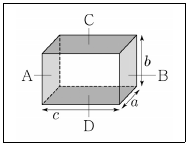
- 2 : 3
- 3 : 2
- 4 : 9
- 9 : 4
4. <보기>는 수은 기둥 기압계와 지점 A, B, C, D를 나타낸 것이다. 이에 대한 설명으로 가장 옳은 것은? (단, B의 높이는 수은면 표면이고, C의 높이는 B의 높이와 같다. 또한 수은 기둥의 위쪽 공간은 진공으로 가정한다.)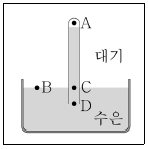
- A의 절대압력은 대기압의 크기에 따라 바뀐다.
- B의 절대압력은 A보다 크고 C보다 작다.
- C의 절대압력은 대기압과 같다.
- D의 절대압력은 C와 같다.
5. 반지름이 R인 내부가 꽉찬 도체 구가 양의 전하량 Q로 대전되어 있다. 이에 대한 설명으로 가장 옳은 것은?
- 도체 구 표면의 전위의 크기는 구의 반지름에 반비례한다.
- 도체 구 중심의 전위는 0 이다.
- 전하는 도체 구 전체에 균일하게 분포한다.
- 도체 구 겉표면의 전기장은 0 이다.
6. 주파수가 5GHz 인 파동이 2μ초 동안 발생하였다. 이 파동의 총 진동 횟수는?
- 10회
- 100회
- 1,000회
- 10,000회
7. <보기>의 빈칸에 들어갈 숫자는?
- 1
- 2
- 5
- 10
8. <보기 1>과 같이 경사각이 θ인 빗면에 수직 방향으로 균일한 자기장이 형성되어 있다. 이 빗면에 저항 R이 연결된 도선을 놓고 그 위에 도체 막대를 가만히 올려 놓아 미끄러져 내려가게 한 후, 시간에 따른 도체 막대의 속력 그래프를 얻었다. 도체 막대의 길이는 ㅣ이고 질량은 m이며, 자기장의 세기는 B 이다. t1초 이후에 도체 막대가 등속운동을 한다고 할 때, <보기 2>에서 옳은 설명을 모두 고른 것은? (단, 모든 마찰은 무시하고, 도선과 도체 막대의 전기 저항도 저항 R에 비해 매우 작다고 가정하여 무시한다. 또한 중력가속도는 g라 한다.)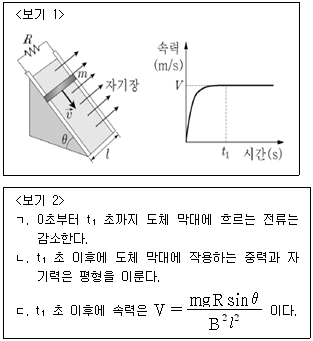
- ㄱ
- ㄴ
- ㄷ
- ㄱ, ㄴ, ㄷ
9. <보기>는 밀도가 균일한 줄에 질량이 4kg인 추를 매달아 벽과 도르래 사이에 걸쳐둔 모습을 나타낸 것이다. 줄의 총 질량은 1kg이고 총 길이는 10m이다. 벽과 도르래를 연결하는 줄에서 파동의 속력[m/s]은? (단, 중력가속도는 10m/s2이며, 도르래의 마찰과 질량은 무시한다.)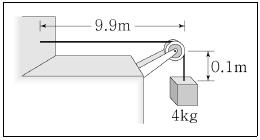
- 5
- 10
- 15
- 20
10. <보기>는 어떤 용수철에 매달린 물체의 단진동운동의 운동에너지 K(t)와 위치에너지U(t)를 시간에 따라 나타낸 것이다. 이에 대한 설명으로 가장 옳지 않은 것은?
- 시간 T/8일 때와 3T/8 일 때 물체의 운동 방향은 반대이다.
- 매시간 운동에너지와 위치에너지의 합은 같다.
- 시간 T/4일 때 물체는 평형 위치에 있다.
- 시간 T동안 물체는 평형 위치를 2번 지난다.
11. 용수철 상수 k=20N/m이고 고유 길이가 1m인 용수철을 질량 2kg인 물체와 연결한 후 마찰이 없는 평면에 놓았다. <보기>와 같이 평면에서 물체가 용수철에 매달려 등속원운동하고 있을 때 용수철의 길이는 1.5m였다. 이때, 용수철에 저장된 탄성에너지와 물체의 운동에너지의 비는? (단, 용수철의 무게는 무시한다.)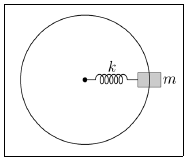
- 1 : 1
- 1 : 1.5
- 1 : 2
- 1 : 3
12. 공기 중에서 운동하는 물체에 작용하는 끌림힘(drag force)은 물체의 운동 방향의 단면적에 비례하고 또한 속력의 제곱에 비례한다. 질량이 M인 물체를 낙하산에 매달아 공중에서 수직으로 떨어뜨렸더니 종단속력 v로 지면에 떨어졌다. 같은 낙하산에 질량이 2M인 물체를 매달아 떨어뜨렸을 때 이 물체의 종단속력은? (단, 두 물체는 충분히 높은 지점에서 떨어졌다고 가정하고 질량을 가진 물체의 크기는 무시한다.)
- 4v
- 2v
- √2v
- v
13. <보기 1>은 어떤 균일한 금속판에 빛을 비추었을 때 측정되는 정지 전압을 빛의 진동수에 따라 나타낸 것이다. <보기 2>에서 옳은 설명을 모두 고른 것은? (단, 전자의 전하량은 -|e| 이고, 플랑크 상수는 h 이다.)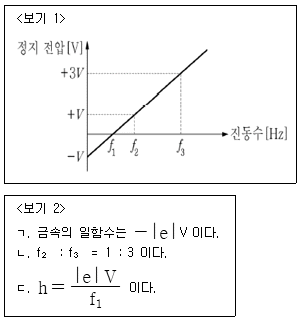
- ㄷ
- ㄱ, ㄴ
- ㄱ, ㄷ
- ㄴ, ㄷ
14. <보기>와 같이 마찰이 없는 수평면 위에 질량이 990g인 물체가 용수철 상수 k=100N/m인 용수철에 연결된 후 정지해 있다. 질량이 10g이고 속력이 5m/s 인 총알이 날아와 정지해있던 물체에 박혀 단조화운동을 한다. 이때 단조화운동의 진폭[mm]은? (단, 총알이 박혔을 때 물체의 모양변화나 기울어짐, 용수철의 무게는 무시한다.)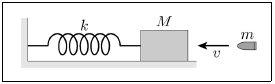
- 1
- 2
- 5
- 10
15. 일치원 무한 퍼텐셜우물에 갇힌 전자의 바닥상태 에너지를 E라 하자. 이 퍼텐셜우물에 갇힌 전자가 방출하는 광자가 가질 수 있는 에너지 값은?
- E
- 2E
- 4E
- 8E
16. <보기>는 마찰이 있는 수평면 위에서 정지한, 질량이 1kg인 물체에 각도 45°로 가해진 힘을 나타낸 것이다. 힘의 크기가 5N일 때 물체는 등가속도 운동을 하였다. 이때 물체의 가속도 크기[m/S2]는? (단, 물체와 수평면 사이의 운동마찰계수는 0.2이고, 중력가속도는 10m/s2 이다. 또한 질량 1kg 물체의 크기는 무시한다.)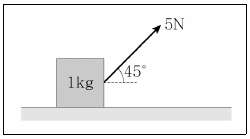
17. <보기>와 같이 반지름이 각각 ra, rb인 원형 도선 a, b에 각각 세기가 일정한 전류가 흐르고 있다. 점 Oa, Ob는 a와 b의 중심이며 a와 b에 흐르는 전류에 의한 자기모멘트의 크기가 같다. Oa, Ob에서 전류에 의한 자기장의 세기를 각각 Ba, Bb라고 할 때, Bb/Ba는?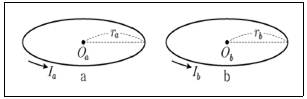
18. <보기>는 굴절률이 4.0 인 기판에 무반사 박막을 코팅한 모습을 나타낸 것이다. 박막의 굴절률이 1.5 일 때, 파장 600nm인 빛의 반사를 최소화하기 위한 박막의 최소두께 [mm]는?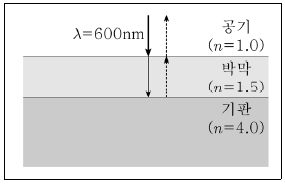
- 100
- 150
- 200
- 250
19. <보기>는 어떤 일정량의 이상기체의 상태변화를 나타낸 것이다. 이에 대한 설명으로 가장 옳은 것은?
- 과정 A → B 동안 기체의 내부에너지는 감소한다.
- 과정 B → C 동안 기체의 엔트로피는 증가한다.
- 과정 C → A 동안 기체의 온도는 증가한다.
- 순환과정 A → B → C → A 에서 기체가 한 일의 합은 10J 이다.
20. 밀도가 ρ=2g/cm3 인 비압축성 유체가 수평관을 통해 정상류를 이루며 흐르고 있다. 이 관에서 높이가 같은 두 지점 A와 B를 생각하자. A 지점에서 유체의 속력은 v = 10cm/s이고 두 지점의 압력 차이는 △p = 150Pa 이다. 이때 두 지점에서 수평관의 지름의 비(dA/dB)는? (단, 수평관의 단면은 원형이고, B 지점의 지름이 더 작다고 가정하며 수평관 내 유체는 베르누이 법칙을 만족한다.)
- 1
- 2
- 4
- 16






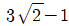
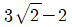
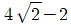
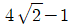
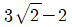 " 이다.
" 이다.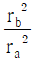
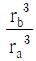
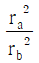
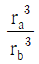
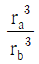 "이다.
"이다.
4초일 때의 속력은 5m/s 이다. 이는 0초에서부터 4초까지의 시간 동안 물체가 이동한 거리를 계산하여 구할 수 있다.
0초에서부터 4초까지의 이동 거리는 다음과 같다.
(0.5) × (4) × (4) = 8m
따라서, 4초일 때의 속력은 8m를 4초로 나눈 값인 2m/s가 아니라, 보기에서 주어진 가속도에 따라 계산한 결과인 5m/s가 된다.
그 외의 보기들은 물체의 운동과는 직접적인 연관성이 없는 내용들이므로, 이 문제와는 무관하다.