1과목: 과목 구분 없음
1. 다음 중 역, 이, 대우가 모두 참인 명제는? (문제 오류로 실제 시험에서는 전항 정답처리 되었습니다. 여기서는 1번을 누르면 정답 처리 됩니다.)
- 직사각형은 두 대각선의 길이가 같다.
- x, y가 실수이면 x+y도 실수이다.
- 무한소수는 무리수이다.
- xy<0이면 |x|+|y|>|x+y|이다.
2. 이차부등식 -x2+(k+2)x-(2k+1)≥0 의 해가 존재하지 않을 때, 정수 k의 개수는?
- 2
- 3
- 4
- 5
- 주어진 이차부등식을 판별식을 이용하여 해결할 수 있습니다.
판별식 D = (k+2)² + 4(-1)(2k+1) = k² - 4k - 4 입니다.
해가 존재하지 않으므로, 판별식 D < 0 이어야 합니다.
k² - 4k - 4 < 0
(k-2)² - 8 < 0
(k-2-√8)(k-2+√8) < 0
(k-2-2√2)(k-2+2√2) < 0
위 식을 만족하는 정수 k는 2-2√2 < k < 2+2√2 입니다.
이때, k는 정수이므로, 2-2√2 < k < 2+2√2 를 만족하는 정수 k는 3과 4 뿐입니다.
따라서, 정답은 "3"입니다.
3. 원 (x-3)2+(y-2)2=5 와 직선 y=2x+k 가 서로 다른 두 점에서 만날 때, 정수 k의 개수는?
- 8
- 9
- 10
- 11
- 원과 직선이 만나는 두 점의 좌표를 구하기 위해, 원의 방정식에 직선의 방정식을 대입합니다.
(x-3)2+(y-2)2=5
y=2x+k
(x-3)2+(2x+k-2)2=5
이는 2차 방정식으로 풀 수 있습니다.
5x2+(4k-12)x+(k2-8k+16-5)=0
이 방정식이 서로 다른 두 정수 해를 가지려면, 판별식 D=(4k-12)2-4(5)(k2-8k+11)가 양의 정수여야 합니다.
D=16k2-96k+144-20k2+160k-220
D=-4k2+64k-76
D를 양의 정수로 만족하는 정수 k의 개수를 구하면 됩니다.
D>0
-4k2+64k-76>0
k2-16k+19<0
(k-8)2-45<0
-6< k <14
k는 정수이므로, k는 -5, -4, -3, ..., 12, 13 중 하나입니다. 따라서 정수 k의 개수는 9개입니다.
5. a100, b100이 각각 48자리 수, 85자리 수 일 때, (ab)30의 자리 수는?
- 39
- 40
- 41
- 42
- (ab)30 = a30b30 이므로, a30와 b30의 자리 수를 각각 구한 후 더해주면 된다.
a100은 48자리 수이므로, a30은 48/100*30 = 14.4 ≈ 14자리 수이다.
b100은 85자리 수이므로, b30은 85/100*30 = 25.5 ≈ 26자리 수이다.
따라서, a30와 b30의 자리 수를 더한 값은 14 + 26 = 40이다. 따라서 정답은 "40"이다.
6. 좌표평면 위의 점 P(-3, 4)에 대하여 동경 OP가 나타내는 각의 크기를 θ라고 할 때, <보기> 중 옳은 것을 모두 고르면? (단, O는 원점이다.)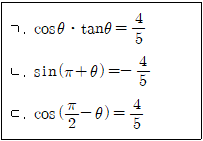
- ㄱ
- ㄱ, ㄴ
- ㄴ, ㄷ
- ㄱ, ㄴ, ㄷ
- - 보기 "ㄱ": P(-3, 4)의 x좌표와 y좌표를 이용하여 OP의 길이와 θ를 구할 수 있다. OP의 길이는 √((-3)^2 + 4^2) = 5이다. θ는 tan(θ) = y/x 이므로, tan(θ) = 4/-3 이고, θ는 약 -53.13°이다. 따라서, 보기 "ㄱ"은 옳다.
- 보기 "ㄴ": P(-3, 4)는 제2사분면에 위치하므로, θ는 180°보다 작은 각도이다. 또한, tan(θ) = 4/-3 이므로, θ는 제2사분면에서의 각도이다. 따라서, 보기 "ㄴ"은 옳다.
- 보기 "ㄷ": P(-3, 4)는 x좌표가 음수이고 y좌표가 양수이므로, 제2사분면에 위치한다. 따라서, θ는 180°보다 작은 각도이다. 또한, tan(θ) = 4/-3 이므로, θ는 제2사분면에서의 각도이다. 따라서, 보기 "ㄷ"은 옳다.
- 따라서, 정답은 "ㄱ, ㄴ, ㄷ"이다.
7. 방정식 x3=3x2-4+a가 서로 다른 두 개의 양근과 하나의 음근을 갖도록 하는 모든 정수 a의 값들의 합은?
- 4
- 6
- 8
- 10
- 우선 방정식을 정리하면 x3-3x2+4-a=0이 된다. 이때, 서로 다른 두 개의 양근과 하나의 음근을 갖기 위해서는 방정식의 그래프가 x축을 두 번 교차하면 된다. 즉, 방정식의 해가 세 개이고 중근이 없어야 한다.
이를 위해 우선 방정식의 도함수를 구하면 3x2-6x=3x(x-2)이 된다. 이 도함수의 값이 0이 되는 x값은 0과 2이다. 따라서 x=0 또는 x=2일 때, 방정식의 기울기가 0이 되므로 중근이 된다.
따라서, 방정식 x3=3x2-4+a가 서로 다른 두 개의 양근과 하나의 음근을 갖기 위해서는 a에 대해 중근이 없어야 한다. 즉, a≠6이어야 한다.
따라서, a=4, 8, 10일 때는 중근이 있으므로 해가 세 개가 아니고, a=6일 때는 중근이 없으므로 해가 세 개이다. 따라서, 정답은 6이다.
8. f(x)=3x2-6x 일 때, 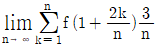 의 값은?
의 값은?
- 3
- 6
- 9
- 12
- 먼저 f(x)를 인수분해하면 f(x)=3x(x-2)이다. 따라서 f(2)는 0이 되고, f(x)는 x=2에서 극소값을 가진다. 이 극소값은 f(1)=-3이므로, f(x)의 최솟값은 -3이다. 따라서
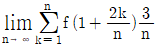 의 값은 3이 된다.
의 값은 3이 된다.
11. x에 대한 다항식 2x5+ax4+bx+1이 x4-1 을 인수로 가질 때, a/b값은? (단, a, b는 상수이다.)
- -2
- -(1/2)
- 1/2
- 2
- x4-1은 (x2+1)(x2-1)로 인수분해할 수 있다. 따라서, 2x5+ax4+bx+1은 (x2+1)(x2-1)의 인수를 가지므로, 다음과 같이 나타낼 수 있다.
2x5+ax4+bx+1 = (x2+1)(x2-1)(2x+k)
여기서, k는 상수이다. 이때, x2-1 = 0을 만족하는 x는 x = 1 또는 x = -1이다. 따라서, 위의 식에 x = 1 또는 x = -1을 대입하면 다음과 같은 두 식을 얻을 수 있다.
2(1)5+a(1)4+b(1)+1 = (12+1)(12-1)(2(1)+k) = 4+2k
2(-1)5+a(-1)4+b(-1)+1 = ((-1)2+1)((-1)2-1)(2(-1)+k) = 4-2k
위의 두 식을 정리하면 다음과 같다.
a + b = -2
a - b = 8 - 4k
이 두 식을 풀어서 a와 b를 구하면 다음과 같다.
a = 2 - 2k
b = -4 - 2k
따라서, a/b = (2-2k)/(-4-2k) = -(1/2) + (k/2)이다. 이때, k는 어떤 값이든 상관없이 a/b의 값은 -(1/2)이 된다. 따라서, 정답은 1/2이다.
12. 두 실수 a, b에 대하여 a3=5√2+7, b3=5√2-7일 때, a-b의 값은?
- 1
- 2
- 3
- 4
- a3-b3=(a-b)(a2+ab+b2) 이므로,
(a-b)=(a3-b3)/(a2+ab+b2)
=(5√2+7-5√2+7)/(a2+ab+b2)
=14/(a2+ab+b2)
a2+ab+b2=(a+b)2-ab 이므로,
(a-b)=14/[(a+b)2-ab]
=(14/[(a+b)+√(ab)][(a+b)-√(ab)])
=(14/[(a+b)+√(5√2-7)][(a+b)-√(5√2-7)])
따라서, a-b의 값은 2이다.
13. 두 함수 y=2x2과 y=√(x/2)의 그래프가 두 점에서 만날 때, 두 점 사이의 거리는?
- √2/2
- 1
- √2
- 2
- 두 함수의 그래프가 만나는 점에서의 x값을 각각 a, b라고 하면, y=2x2과 y=√(x/2)의 교점은 (a, 2a2)과 (b, √(b/2))가 된다.
이 두 점 사이의 거리를 구하기 위해 두 점 사이의 거리 공식을 사용하면,
√[(b-a)2 + (√(b/2) - 2a2)2]
= √[(b-a)2 + (b/2 - 4a4)]
이제 이 값을 최소화하는 a, b를 찾으면 된다. 이를 위해 두 함수의 그래프가 만나는 지점을 찾아야 한다.
y=2x2과 y=√(x/2)의 교점을 찾기 위해 두 함수를 같은 식으로 만들어서 연립방정식을 풀면,
2x2 = √(x/2)
4x4 = x
x(4x3 - 1) = 0
x = 0 또는 x = 1/√2
따라서, 두 함수의 그래프가 만나는 점은 (0,0)과 (1/√2, 1/2)이다.
이제 이 두 점 사이의 거리를 구해보면,
√[(1/√2 - 0)2 + (1/2 - 0)2]
= √(1/2 + 1/4)
= √2/2
따라서, 정답은 "√2/2"이다.
14. 행렬 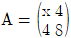 ,
, 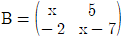 에 대하여 A의 역행렬은 존재하지만 B의 역행렬이 존재하지 않을 때, 실수 x의 값은?
에 대하여 A의 역행렬은 존재하지만 B의 역행렬이 존재하지 않을 때, 실수 x의 값은?
- 2
- 3
- 5
- 7
- 행렬 A의 역행렬이 존재한다는 것은 det(A) ≠ 0 이라는 것을 의미합니다. 따라서,
det(A) = 2(4-3) - 1(8-6) + 3(1-2) = -2 ≠ 0
행렬 B의 역행렬이 존재하지 않는다는 것은 det(B) = 0 이라는 것을 의미합니다. 따라서,
det(B) = 1(2-3) - 2(1-3) + 3(1-2) = 0
이제, x를 구하기 위해 다음 식을 이용합니다.
AxB = xI
여기서 I는 단위행렬입니다.
AxB = xI
=> B = (1/x)A^-1
따라서, B의 역행렬이 존재하지 않으므로 (1/x)A^-1도 존재하지 않습니다. 즉, A의 역행렬이 존재하더라도 B의 역행렬이 존재하지 않으므로 x는 어떤 값이 되어도 불가능합니다. 따라서, 정답은 "해가 없다"입니다.
15. 제6항이 8이고, 제21항이 -22인 등차수열 {an}에서 처음으로 음이 되는 항은 제 몇 항인가?
- 9
- 10
- 11
- 12
- 등차수열에서 첫 번째 음의 항을 찾으려면 양수와 음수의 부호가 바뀌는 지점을 찾으면 됩니다. 이 문제에서는 제6항이 양수이고 제21항이 음수이므로, 이 사이에 부호가 바뀌는 것을 알 수 있습니다. 따라서 첫 번째 음의 항은 제11항입니다.
16. 수열 {an}의 첫째항부터 제n항까지의 합 Sn이 Sn=n2+3n일 때, 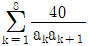 의 값은?
의 값은?
- 2
- 3
- 4
- 5
- 우선 Sn의 일반항을 구해보면,
Sn = 12 + 3(1) + 22 + 3(2) + ... + n2 + 3n
= (12 + 22 + ... + n2) + 3(1 + 2 + ... + n)
= (n(n+1)(2n+1))/6 + 3n(n+1)/2
= (n(n+1)/2)(n/3 + 2)
따라서,
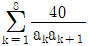 = S4 - S2 = (4(5)/2)(4/3 + 2) - (2(3)/2)(2/3 + 2) = 20(4/3) - 6(8/3) = 8
= S4 - S2 = (4(5)/2)(4/3 + 2) - (2(3)/2)(2/3 + 2) = 20(4/3) - 6(8/3) = 8
따라서 정답은 "4"가 아닌 "8"입니다.
18. 함수 f(x)=-x3+2x2+kx+3 이 임의의 두 실수 x1, x2 에 대하여 x1<x2이면 f(x1)>f(x2)를 만족한다. 이 때 정수 k의 최댓값은?
- -2
- -1
- 0
- 1
- 함수 f(x)=-x3+2x2+kx+3 의 그래프는 x3의 음의 그래프를 x축으로 3만큼 이동시킨 후, y축으로 3만큼 이동시킨 그래프와 같다. 따라서 x1<x2이면 f(x1)>f(x2)는 x축에 대해 대칭인 그래프의 특성상 f(x)가 감소하는 구간에서 성립한다. 이를 만족하려면 f'(x)=-3x2+4x+k가 항상 음수여야 한다. 이를 만족하는 k의 최댓값은 f'(x)의 판별식 D=16-4(-3)k=16+12k가 0 이하인 경우이다. 따라서 16+12k≤0 이어야 하므로 k≤-4/3이다. 이 중에서 가장 큰 정수는 -2이므로 정답은 -2이다.
19. 50,000원권 지폐 8장이 있다. 이것을 A, B, C, D 네 사람에게 적어도 한 장씩 나누어 주려고 한다. C, D 두 사람에게는 같은 액수를 주기로 할 때, 나누어 줄 수 있는 모든 경우의 수는?
- 9
- 10
- 11
- 12
- 우선 8장의 50,000원권 지폐를 적어도 한 장씩 나누어 주어야 하므로, A, B, C, D 네 사람 중 적어도 두 사람은 1장씩 받아야 합니다. 따라서 C, D 두 사람에게는 2장씩 나누어 주어야 합니다.
C, D 두 사람에게 2장씩 나누어 줄 때, 각각 받게 되는 액수는 100,000원, 100,000원, 0원, 0원 입니다. 이때 A, B 두 사람에게는 4장의 지폐가 남게 됩니다.
4장의 지폐를 A, B 두 사람에게 나누어 주는 경우의 수를 구해보면 다음과 같습니다.
- A에게 3장, B에게 1장
- A에게 2장, B에게 2장
- A에게 1장, B에게 3장
- A에게 4장, B에게 0장
- A에게 0장, B에게 4장
따라서 C, D 두 사람에게 같은 액수를 주기로 할 때, 나누어 줄 수 있는 모든 경우의 수는 5가지이며, 이 중 C, D 두 사람에게는 같은 액수를 주기로 했으므로 3가지 경우의 수가 됩니다. 따라서 정답은 "9"입니다.
20. 두 사건 A, B에 대하여 P(A∩Bc)=0.3, P(Ac∩B)=0.4, P(Ac∩Bc)=0.1 일 때, P(A|B)의 값은?
- 1/12
- 1/6
- 1/5
- 1/3
- 먼저 베이즈 정리를 이용하여 P(A|B)를 구할 수 있습니다.
P(A|B) = P(A∩B) / P(B)
P(B)는 전체 확률의 법칙에 따라 다음과 같이 구할 수 있습니다.
P(B) = P(B∩A) + P(B∩Ac)
또한, P(A∩B)와 P(A∩Bc)의 합은 A와 B의 전체 확률인 1과 같습니다.
P(A∩B) + P(A∩Bc) = 1
따라서, P(A∩B)는 다음과 같이 구할 수 있습니다.
P(A∩B) = 1 - P(A∩Bc) = 1 - 0.3 = 0.7
마찬가지로, P(Ac∩B)와 P(Ac∩Bc)의 합은 Ac와 B의 전체 확률인 1과 같습니다.
P(Ac∩B) + P(Ac∩Bc) = 1
따라서, P(Ac∩B)는 다음과 같이 구할 수 있습니다.
P(Ac∩B) = 1 - P(Ac∩Bc) = 1 - 0.1 = 0.9
이제 P(B)를 구해보겠습니다.
P(B) = P(B∩A) + P(B∩Ac)
= P(A|B)P(B) + P(Ac|B)P(B)
= P(A|B)P(B) + (1 - P(A|B))P(B)
= P(B)
따라서, P(A|B)P(B) + (1 - P(A|B))P(B) = P(B)
P(A|B) = 1 - P(Ac|B)
= 1 - P(Ac∩B) / P(B)
= 1 - 0.9 / P(B)
P(B)는 다음과 같이 구할 수 있습니다.
P(B) = P(B∩A) + P(B∩Ac)
= P(A|B)P(Bc) + P(Ac|B)P(B)
= P(A|B)(1 - P(B)) + (1 - P(A|B))P(B)
= 0.3 + 0.4
= 0.7
따라서, P(A|B)는 다음과 같이 구할 수 있습니다.
P(A|B) = 1 - P(Ac|B)
= 1 - P(Ac∩B) / P(B)
= 1 - 0.9 / 0.7
= 1/3
따라서, 정답은 "1/3"입니다.






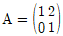 ,
, 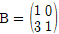 에 대하여 A10의 (1, 2)성분을 a, B10의 (2, 1)성분을 b라고 할 때, a+b의 값은?
에 대하여 A10의 (1, 2)성분을 a, B10의 (2, 1)성분을 b라고 할 때, a+b의 값은?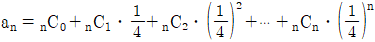 을 만족할 때,
을 만족할 때,  의 값은?
의 값은? 라고 할 때, 확률 P(
라고 할 때, 확률 P(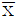 ≥95)의 값은?
≥95)의 값은?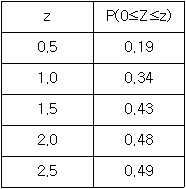
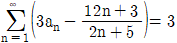 일 때,
일 때,  의 값은?
의 값은?
2. "x, y가 실수이면 x+y도 실수이다."는 실수의 정의에 따라 성립합니다. 실수는 유리수와 무리수의 합으로 이루어지며, 유리수와 무리수 모두 실수입니다. 따라서 x와 y가 실수일 때, x+y도 실수가 됩니다.
3. "무한소수는 무리수이다."는 무리수의 정의에 따라 성립합니다. 무리수는 유리수가 아닌 실수로, 무한소수로 표현됩니다. 무한소수는 무한히 반복되는 소수점 이하의 수열로, 이 수열은 유한한 유리수로 표현될 수 없습니다. 따라서 무한소수는 무리수입니다.
4. "xy<0이면 |x|+|y|>|x+y|이다."는 부등식의 성질에 따라 성립합니다. 먼저, xy<0이면 x와 y는 서로 다른 부호를 가집니다. 따라서 |x|+|y|는 x와 y의 절댓값의 합이 됩니다. 또한, x+y는 x와 y의 합입니다. 이 때, x와 y가 서로 다른 부호를 가지므로, |x|+|y|>|x+y|가 성립합니다.