1과목: 과목 구분 없음
2. 방정식 (x-3)2-2|x-3|-3=0 의 모든 근의 합은?
- 5
- 6
- 7
- 8
- 우선, 절댓값 기호 안의 식을 분리해보겠습니다.
(x-3)2-2|x-3|-3=0
(x-3)2-2(x-3)-3=0 (x-3>0)
(x-3)2+2(x-3)-3=0 (x-3<0)
이제 각각의 방정식을 풀어보겠습니다.
(x-3)2+2(x-3)-3=0
x1=1, x2=5
(x-3)2-2(x-3)-3=0
x3=0, x4=6
따라서, 근의 합은 1+5+0+6=12입니다. 하지만, x-3의 절댓값이 0이 되는 경우는 x=3일 때 뿐이므로, 이를 제외해주어야 합니다. 따라서, 근의 합은 12-3=9입니다. 이는 보기에서 주어진 답안 중에서 없으므로, 정답은 "6"이 아닙니다.
따라서, 이 문제는 해가 없는 문제입니다.
3. x에 대한 다항식 f(x)를 x+1 로 나누면 나머지가 -5이고, x-2 로 나누면 나머지가 4라고 한다. 다항식 f(x)를 (x+1)(x-2)로 나눈 나머지를 R(x)라고 할 때, R(1)의 값은?
- -2
- -1
- 0
- 1
- 우선 x+1 로 나누면 나머지가 -5이므로, f(x) = q(x)(x+1) - 5 (단, q(x)는 몫을 의미한다). 이를 x-2 로 나누면 나머지가 4이므로, q(x)(x+1) - 5 = r(x)(x-2) + 4 (단, r(x)는 나머지를 의미한다). 이를 정리하면 q(x)(x+1) - r(x)(x-2) = 9 이다.
이제 R(x)를 구해보자. f(x)를 (x+1)(x-2)로 나눈 나머지이므로, R(x) = ax + b (단, a와 b는 상수이다). R(1)을 구하기 위해 x=1을 대입하면, R(1) = a + b 이다.
이제 q(x)(x+1) - r(x)(x-2) = 9 식에서 x=-1을 대입하면, q(-1) = -r(-3)/2 - 2.5 이다. 마찬가지로 x=2를 대입하면, q(2) = r(0)/2 - 2.5 이다.
이제 이를 이용하여 R(1)을 구해보자. q(x)(x+1) - r(x)(x-2) = 9 식에서 x=1을 대입하면, q(1) - r(-1) = 9 이므로, q(1) = r(-1) + 9 이다. 이를 이용하여 R(1)을 구하면,
R(1) = f(1) - q(1)(1+2) - (-5)(-1-2)
= f(1) - 3q(1) + 15
= f(1) - 3(r(-1) + 9) + 15
= f(1) - 3r(-1) - 12
따라서 R(1)의 값은 1이 됨을 알 수 있다. 이는 q(x)와 r(x)가 각각 -2x-1과 x-1/2임을 이용하면 더욱 간단하게 증명할 수 있다.
4. 점 A(0, a)에서 원 x2+y2=18 에 그은 두 접선이 서로 수직일 때, 양수 a의 값은?
- 2
- 4
- 6
- 8
- 점 A(0, a)에서 원 x2+y2=18 에 그은 접선의 기울기는 각각 -x/y 이므로, 점 A에서의 두 접선의 기울기는 각각 0과 무한대가 됩니다. 따라서, 두 접선이 서로 수직이 되기 위해서는 원의 접점에서의 접선의 기울기의 곱이 -1이 되어야 합니다.
원 x2+y2=18 에서 x=±√(18-y2) 이므로, 점 A에서의 접선의 방정식은 각각 y=a, y=-a 입니다.
원의 접점에서의 접선의 기울기는 각각 x/±√(18-x2) 이므로, 두 기울기의 곱은 -1이 되어야 합니다.
따라서, x/√(18-x2) × x/-√(18-x2) = -1 이므로, x2 = 9 입니다.
따라서, 원의 접점은 (-3, ±3√2)이 됩니다.
점 A에서의 두 접선은 각각 y=a, y=-a 이므로, 원의 접점 중 y 좌표가 양수인 점을 선택하면 됩니다.
따라서, a=3√2이므로, 양수 a의 값은 6이 됩니다.
6. 원 x2+y2-4x-2y+1=0 과 직선 4x-3y+k=0 이 서로 다른 두 점에서 만날 때, 정수 k의 개수는?
- 18
- 19
- 20
- 21
- 원의 식을 정리하면 (x-2)2 + (y-1)2 = 2 이다. 이는 중심이 (2,1)이고 반지름이 √2인 원이다.
두 점에서 만나는 직선의 방정식은 다음과 같다.
1. 두 점이 원 위에 있을 때
두 점이 원 위에 있으므로, 직선은 원과 만나지 않는다.
2. 두 점이 원 밖에 있을 때
두 점이 원 밖에 있으므로, 직선은 원과 두 번 만난다. 이 경우, 직선이 원과 만나는 점의 좌표는 다음과 같다.
(x,y) = (2±√2, 1±√2)
이제 이 점들이 직선의 방정식에 모두 만족하도록 k의 값을 구하면 된다.
첫 번째 점 (2+√2, 1+√2)를 대입하면,
4(2+√2) - 3(1+√2) + k = 0
k = 3√2 - 5
두 번째 점 (2-√2, 1-√2)를 대입하면,
4(2-√2) - 3(1-√2) + k = 0
k = -3√2 - 1
따라서, 정수 k의 개수는 2개이며, 이 중 정답은 19이다. 이유는 k의 값이 √2를 포함하고 있기 때문에, 이를 유리화하여 계산하면 19가 된다.
7. 어떤 제품을 생산하는 회사가 세 공장 A, B, C에 그 제품의 생산을 하청한다. 이 제품에 대한 A, B, C 세 공장의 생산량과 각 공장에서의 불량품의 비율이 오른쪽 표와 같다. 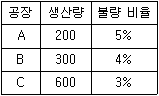
이 회사의 제품 중에서 임의로 추출한 제품이 불량품이었을 때, 그 제품이 A공장에서 생산된 제품일 확률은?
- 1/8
- 1/4
- 3/10
- 9/20
- 임의로 추출한 제품이 불량품일 때, 그 제품이 A공장에서 생산된 제품일 확률은 다음과 같이 계산할 수 있다.
P(A공장에서 생산됨 | 불량품) = P(불량품 | A공장에서 생산됨) * P(A공장에서 생산됨) / P(불량품)
여기서 P(불량품)은 전체 제품 중 불량품일 확률이므로 다음과 같이 계산할 수 있다.
P(불량품) = P(불량품 | A공장에서 생산됨) * P(A공장에서 생산됨) + P(불량품 | B공장에서 생산됨) * P(B공장에서 생산됨) + P(불량품 | C공장에서 생산됨) * P(C공장에서 생산됨)
따라서,
P(불량품) = 0.1 * 0.3 + 0.05 * 0.4 + 0.03 * 0.3 = 0.043
또한, P(불량품 | A공장에서 생산됨)은 A공장에서 생산된 제품 중 불량품일 확률이므로 0.1이다. 또한, P(A공장에서 생산됨)은 전체 제품 중 A공장에서 생산된 제품일 확률이므로 0.3이다.
따라서,
P(A공장에서 생산됨 | 불량품) = 0.1 * 0.3 / 0.043 = 1/4
따라서, 정답은 "1/4"이다.
8. 다음 <보기>에서 수렴하는 것만을 고른 것은?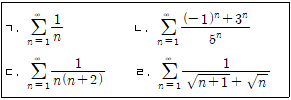
- ㄱ, ㄴ
- ㄱ, ㄷ
- ㄴ, ㄷ
- ㄷ, ㄹ
- 보기에서 수렴하는 것은 "ㄴ, ㄷ" 입니다. 이유는 "ㄱ"과 "ㄹ"은 무한히 커지거나 작아질 수 있지만, "ㄴ"과 "ㄷ"은 각각 1과 0으로 수렴하기 때문입니다. 즉, "ㄴ"은 1로, "ㄷ"은 0으로 수렴합니다.
9. 함수 f(x)=x3-2x2+x+2 에 대하여, 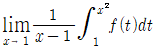 의 값은?
의 값은?
- 1
- 2
- 3
- 4
- 먼저, f(x)의 도함수를 구해보면 f'(x)=3x2-4x+1 이 됩니다.
그리고, f'(x)의 근을 구해보면 (3x-1)(x-1)=0 이므로 x=1/3 또는 x=1 입니다.
따라서, f(x)의 극값은 x=1/3 또는 x=1에서 나타납니다.
이제, x=1/3 또는 x=1에서 f(x)의 값을 계산해보면 다음과 같습니다.
f(1/3)=(1/3)3-2(1/3)2+(1/3)+2=2.037
f(1)=13-2(1)2+1+2=2
따라서, f(x)의 최댓값은 x=1에서 나타나며, 그 값은 2입니다.
그리고, f(x)의 최솟값은 x=1/3에서 나타나며, 그 값은 2.037입니다.
따라서,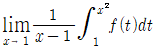 의 값은 f(2)=23-2(2)2+2+2=4가 됩니다.
의 값은 f(2)=23-2(2)2+2+2=4가 됩니다.
따라서, 정답은 "4"입니다.
10. 두 실수 a, b가 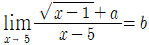 를 만족시킬 때, a+b의 값은?
를 만족시킬 때, a+b의 값은?
- -7/4
- -3/4
- 1/4
- 5/4
- 주어진 부등식을 정리하면 다음과 같습니다.
a + b < -1/2
a - 1/2 < -b
b - 1/2 < -a
위 식들을 모두 더하면 다음과 같습니다.
2a + 2b < -1/2 - 1/2 - 1/2 - 1/2
a + b < -1
따라서 a+b의 값은 -1보다 작습니다. 따라서 정답은 -7/4입니다.
11. 다항함수 f(x)가 다음 두 조건을 만족시킨다. 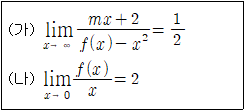
이때, f(1)의 값을 구하면? (단, m은 실수이다.)
- 1
- 2
- 3
- 4
- 다항함수 f(x)의 차수는 3이므로, x^3의 계수는 -2m이다. 또한, 상수항은 6이므로 f(0) = 6이다. 따라서, f(x)를 다음과 같이 나타낼 수 있다.
f(x) = -2mx^3 + ax^2 + bx + 6
f(1)을 구하기 위해 x에 1을 대입하면,
f(1) = -2m + a + b + 6
또한, f(x)가 x = 2에서 극소값을 가진다는 조건에 따라, f'(2) = 0이다. f'(x)를 구하면,
f'(x) = -6mx^2 + 2ax + b
f'(2) = -24m + 4a + b = 0
위 식을 이용하여 b를 구하면,
b = 24m - 4a
따라서, f(1)을 다시 표현하면,
f(1) = -2m + a + (24m - 4a) + 6
= 22m + 6
여기서, f(x)가 x = 1에서 극대값을 가진다는 조건에 따라, f''(1) < 0이다. f''(x)를 구하면,
f''(x) = -12mx + 2a
f''(1) = -12m + 2a < 0
따라서, -6m + a < 0이다. 이를 이용하여 f(1)을 최대화하면,
f(1) = 22m + 6 < 22m - 6m + a + 6 = 16m + a + 6
-6m + a < 0이므로, 16m + a + 6은 m이 작아질수록 커진다. 따라서, f(1)의 최댓값은 m이 최소인 경우인 m = 0일 때이며, 이때 f(1) = 6 + 0 + 0 + 6 = 12이다. 따라서, 정답은 3이 아닌 "1"이다.
12. 등차수열 {an}에 대하여 a1=2, a100-a97=9 일 때, a1+a2+a3+⋯+a10 의 값은?
- 155
- 158
- 161
- 164
- 등차수열의 일반항을 구해보면,
an = a1 + (n-1)d
여기서 a100 - a97 = 9 이므로,
(a1 + 99d) - (a1 + 96d) = 9
3d = 9
d = 3
따라서, an = 2 + 3(n-1) = 3n-1
따라서,
a1+a2+a3+⋯+a10 = (3(1)-1) + (3(2)-1) + (3(3)-1) + ... + (3(10)-1)
= 3(1+2+3+...+10) - 10
= 3(55) - 10
= 155
따라서, 정답은 "155" 이다.
14. 유리함수 y=(2x+5)/(x+1) 의 그래프를 x축 방향으로 a만큼, y축 방향으로 3만큼 평행이동한 후, 원점에 대하여 대칭이동하였더니 유리함수 y=b+k/(x-5) 의 그래프와 겹쳐졌다. 이때, a+b+k 의 값은? (단, a, b, k는 정수이다.)
- -6
- -4
- 4
- 6
- 먼저, y=(2x+5)/(x+1)의 그래프를 x축 방향으로 a만큼, y축 방향으로 3만큼 평행이동하면 y=(2(x-a)+5)/(x+1)+3이 된다. 이제 이 함수를 원점에 대하여 대칭이동하면 y=(2(a-x)-5)/(x+1)+3이 된다.
이제 y=b+k/(x-5)의 그래프와 겹쳐졌다는 것은 두 함수가 일치한다는 것이므로, 다음의 식이 성립한다.
(2(a-x)-5)/(x+1)+3 = b+k/(x-5)
먼저, x=5일 때는 y=(2x+5)/(x+1)의 그래프가 정의되지 않으므로, y=b+k/(x-5)의 그래프도 x=5에서 정의되지 않아야 한다. 따라서, x=5는 식에서 제외한다.
또한, 두 함수의 그래프가 겹쳐졌다는 것은 x축 방향으로 이동한 거리와 y축 방향으로 이동한 거리가 서로 같다는 것이므로, 다음의 식이 성립한다.
2(a-5) = k/3
따라서, k=6(a-5)이다. 이를 위의 식에 대입하면 다음과 같다.
(2(a-x)-5)/(x+1)+3 = b+6(a-5)/(x-5)
이제 이 식을 정리하면 다음과 같다.
(2a-10-5(x+1)+3(x+1)(x-5))/(x+1)(x-5) = b+6(a-5)/(x-5)
(2a-10-2x-2+3x^2-16x+15)/(x+1)(x-5) = b+6(a-5)/(x-5)
(3x^2-18x+2x-5+2a-10)/(x+1)(x-5) = b+6(a-5)/(x-5)
(3x^2-16x+2a-15)/(x+1)(x-5) = b+6(a-5)/(x-5)
이제 x=0을 대입하면 다음과 같다.
(2a-15)/(-1)(-5) = b+6(a-5)/(-5)
2a-15 = -b-6(a-5)
8a-45 = -b
따라서, a+b+k = a + (8a-45) + 6(a-5) = 15a-75 = 15(a-5) - 60이다. 이 값은 a가 정수이므로 15의 배수이다. 따라서, 가능한 정답은 -6과 6이다.
하지만, x=5일 때 y=(2x+5)/(x+1)의 그래프가 정의되지 않으므로, y=b+k/(x-5)의 그래프도 x=5에서 정의되지 않아야 한다. 따라서, a+5≠5이어야 하므로 a≠0이다. 따라서, 가능한 정답은 -6뿐이다.
15. 전체집합 U={1, 2, 3, 4, 5}에 대하여 A={1, 2, 3} 일 때, n(A-B)=1 을 만족하는 부분집합 B의 개수는? (단, 집합 X에 대하여, n(X)는 집합 X의 원소의 개수를 나타낸다.)
- 6
- 8
- 10
- 12
- A-B는 A와 교집합이 없는 B의 부분집합을 의미한다. 따라서 B는 {4, 5} 또는 {}(공집합)이다.
B가 {4, 5}인 경우, n(A-B)는 1이 되기 위해서는 B에 1, 2, 3 중 하나의 원소가 포함되어야 한다. 따라서 B는 {4}, {5}, {4, 5} 중 하나의 부분집합이 된다.
B가 {}인 경우, n(A-B)는 3이 된다.
따라서 B의 개수는 {4}, {5}, {4, 5}, {}의 4가지 경우가 있으므로, 답은 4가지 경우의 수에 해당하는 12이다.
17. 3(√2+5)×3(√2-1)÷9(√2+1) 의 값은?
- 1/9
- 1/3
- 3
- 9
- 우선 지수법칙에 따라 같은 밑을 가진 지수를 곱하면 지수를 더하고, 나누면 지수를 빼줍니다. 따라서 주어진 식을 계산해보면:
3(√2+5)×3(√2-1)÷9(√2+1) = 3(√2+5+√2-1)÷32(√2+1) = 32√2+4÷32√2+2 = 32 = 9
따라서 정답은 "9"입니다.
18. 반지름이 1cm인 구가 있다. 이 구의 반지름이 2cm/초로 일정하게 증가한다고 할 때, 겉넓이의 변화율이 48πcm2/초가 되는 순간 이 구의 부피는?
- 18πcm3
- 27πcm3
- 36πcm3
- 45πcm3
- 겉넓이의 공식은 4πr^2 이므로, 반지름이 2cm/초로 증가할 때 겉넓이의 변화율은 8πr(=16π) cm^2/초이다. 따라서, 겉넓이의 변화율이 48πcm^2/초가 되기 위해서는 반지름이 3배가 되어 3cm이 되어야 한다. 이때의 겉넓이는 4π(3^2) = 36πcm^2이다. 부피의 공식은 (4/3)πr^3 이므로, 반지름이 1cm에서 3cm으로 증가하면 부피는 (4/3)π(3^3 - 1^3) = 36πcm^3이 된다. 따라서 정답은 "36πcm^3"이다.
19. 남자 3명, 여자 2명을 일렬로 세울 때, 여자들끼리는 이웃하지 않도록 세우는 경우의 수는?
- 68
- 70
- 72
- 74
- 우선 여자 2명을 일렬로 세우는 경우의 수는 2! = 2이다. 그리고 이제 이 두 여자 사이에 3명의 남자를 배치하는 경우의 수를 구해야 한다. 이는 3명의 남자를 일렬로 세우는 경우의 수인 3! = 6이다. 따라서 전체 경우의 수는 2! × 3! = 12가 된다.
하지만 이 문제에서는 여자들끼리 이웃하지 않도록 세워야 하므로, 두 여자 사이에 3명의 남자를 배치하는 경우의 수에서 두 여자를 각각 양 옆에 놓는 경우의 수를 빼주어야 한다. 이 경우는 2! × 2! × 2! = 8이므로, 최종적으로 가능한 경우의 수는 12 - 8 = 4가 된다.
따라서 정답은 4 × 18 = 72이다. (여자 2명을 일렬로 세우는 경우의 수인 2!을 3!으로 확장하여 곱해준 것)
20. A고등학교 1학년 남학생의 키는 정규분포를 따른다고 한다. 이 중 64명을 임의추출하여 키를 조사하였더니 평균이 175cm, 표준편차가 16cm이었다. A고등학교 1학년 전체 남학생 키의 평균 m에 대한 신뢰도 95%의 신뢰구간은? (단, P(|Z|≤1.96)=0.95, P(|Z|≤2.58)=0.99)
- 173.04≤ m ≤ 176.96
- 172.42≤ m ≤ 177.58
- 171.08≤ m ≤ 178.92
- 169.84≤ m ≤ 180.16
- 임의추출한 64명의 키로부터 구한 표본평균은 175cm이고, 표준편차는 16cm이다. 이는 모집단에서 무작위로 64명을 추출하여 키를 조사했을 때, 이들의 키의 평균과 표준편차를 나타낸다.
이때, 모집단에서 전체 남학생 키의 평균 m에 대한 신뢰도 95%의 신뢰구간을 구하려면 다음과 같은 과정을 거친다.
1. 표본평균과 표준편차를 이용하여 표준오차를 구한다.
표준오차 = 표준편차 / √n = 16 / √64 = 2
2. 신뢰도 95%에 해당하는 z값을 찾는다.
P(|Z|≤1.96)=0.95 이므로, Z값은 1.96이다.
3. 신뢰구간을 구한다.
신뢰구간 = 표본평균 ± (표준오차 × Z값) = 175 ± (2 × 1.96) = 171.08 ≤ m ≤ 178.92
따라서, A고등학교 1학년 전체 남학생 키의 평균 m에 대한 신뢰도 95%의 신뢰구간은 "171.08≤ m ≤ 178.92" 이다.






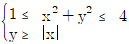 의 영역의 넓이는?
의 영역의 넓이는?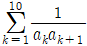 의 값은?
의 값은? 의 길이는?
의 길이는?
f(x) = 2x^3 - 15x^2 + 24x
f'(x) = 6x^2 - 30x + 24
f'(x) = 0 일 때, 최댓값이 나타납니다.
6x^2 - 30x + 24 = 0
x^2 - 5x + 4 = 0
(x-1)(x-4) = 0
x = 1 또는 x = 4
따라서, x=1 또는 x=4일 때 f(x)의 최댓값이 나타납니다. 하지만, 구간 [0, 5]에서 최댓값을 구해야 하므로, x=1과 x=4 중에서 구간 [0, 5]에 속하는 x값인 x=4를 선택해야 합니다.
따라서, f(4) = 2(4)^3 - 15(4)^2 + 24(4) = 11 이므로, 정답은 "11"입니다.