1과목: 과목 구분 없음
1. 부등식 |x|+|x-2|≤5의 해가 a≤x≤b일 때, a+b의 값은?
- -1
- 0
- 1
- 2
2. 방정식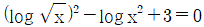 
의 서로 다른 두 근을 α, β라 할 때, αβ의 값은?
- 106
- 107
- 108
- 109
3. 주사위 한 개를 두 번 던져서 처음에 나온 수를 m, 나중에 나온 눈의 수를 n이라고 하자. m+n이 짝수일 때, m이 3의 배수일 확률은?
- 1/4
- 1/3
- 1/2
- 2/3
4. 양의 실수 x에 대하여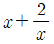 
는 x=a에서 최솟값 b를 가질 때, b/a의 값은? (단, a, b는 상수)
- 2
- 4
- 6
- 8
5. 함수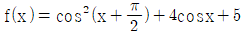 
가 x=a에서 최솟값 b를 가질 때, sin a+b의 값은? (단, 0＜x＜2π)
- -1
- 0
- 1
- 2
6. 수열 {an}의 첫째항부터 제n항까지의 합을 Sn이라 하자. 모든 자연수 n에 대하여 Sn=n2+1을 만족시킬 때,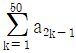 
의 값은?
- 4950
- 4951
- 4952
- 4953
7. 좌표평면 위에서 두 직선 l1 : x+y-2=0, l2 : ax+by-1=0의 교점이 (1, 1)이며, 직선 l1과 l2가 이루는 각을 θ(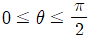 
)라 할 때, 
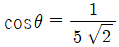이다. |a-b|의 값은?
- 4
- 5
- 6
- 7
8. 
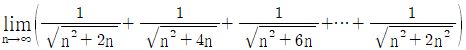의 값은?
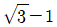
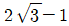
- 2
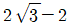
9. 좌표평면 위의 두 점 A(2, 1), B(4, 2)에 대해 선분 AB를 빗변으로 하는 직각 삼각형의 넓이의 최댓값은?
- 1
- 5/4
- 2
- 5/2
10. 집합 X={1, 2, 3, 4, 5}에 대하여 ＜보기＞의 조건을 만족시키는 X에서 X로 가는 함수 f의 개수는?
- 59
- 65
- 78
- 81
11. 직선 y=x+b를 y=x에 대하여 대칭이동하면 원 (x-2)2+y2=1 과 접한다. 이때 b의 값이 될 수 있는 것은?
- 2-√2
- 2
- 4-√2
- 4+√2
12. 다항식 f(x)=x4+ax3+2ax+5를 x+1로 나눈 나머지와 f(x)를 x2+2로 나눈 나머지가 같을 때, 상수 a의 값은?
- -2
- -1
- 1
- 2
13. 함수 f(x)=(a+1)x2+2(1-a)x+a-2의 그래프가 a의 값에 관계없이 항상 지나는 점을 P라 하자. 곡선 y=f(x) 위의 점 P에서의 접선의 y절편은?
- -3
- -2
- 2
- 3
14. 실수 전체의 집합에서 미분가능한 함수 f(x)가 모든 실수 x,y에 대하여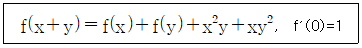 
을 만족할 때, f(1)의 값은?
- 1/2
- 1
- 4/3
- 2
15. 조표공간의 두 점 A(2, 1, 1), B(3, 2, 2)와 xy평면 위를 움직이는 점 P에 대하여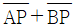 
의 최솟값은?
- 2√3
- √11
- √0
- 3
16. 함수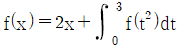 
에 대하여 f(10)의 값은?
- 9
- 10
- 11
- 12
17. 두 곡선 y=-x2+4와 y=x2-2x로 둘러싸인 부분의 넓이는?
- 6
- 7
- 8
- 9
18. 삼차함수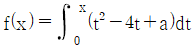 
가 모든 실수 x에 대하여 항상 증가하는 함수가 되도록 하는 실수 a의 최솟값은?
- 1
- 2
- 3
- 4
19. 이차방정식 x2+ax+b=0의 두 실근을 α, β(α＜β)라 할 때, 1/α, α, 1/β이 이순서로 등비수열로 이루고, α, 4b, β가 이 순서로 등차수열을 이룬다. β-α의 값은?
- √3
- 2
- √5
- 2√2
20. 다항함수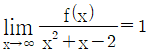 
, 
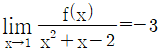을 만족시킬 때, f(0)의 값은?
- 6
- 8
- 10
- 12