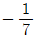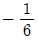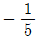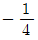1과목: 과목 구분 없음
1. 곡선 y=g(x)의 그래프를 유리함수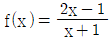 
의 그래프를 x축의 방향으로 a만큼, y축의 방향으로 b만큼 평행이동한 것이다. (g ∘ f)(x)=x 일 때, a+b의 값은?
- -2
- -1
- 0
- 1
2. 실수 x, y에 대하여 18x = 9, 4y = 3일 때,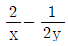 
의 값은?
- 1
- 2
- 3
- 4
3. 이차방정식 x2-px+p=0의 두 근이 sinθ, cosθ 일 때, p2-2p 의 값은?
- 1
- 2
- -1
- -2
4. 방정식 x2+y2+2mx+2(m+1)y+4m2+10m+7=0이 원을 나타내기 위한 실수 m에 대하여 이 원의 반지름의 최댓값은?
- 1
- √2
- 2
- √3
5. 이차방정식 x2+x+1=0의 한 근을 ω라고 할 때,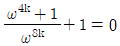 
을 만족하는 100 이하의 자연수 k의 개수는?
- 63
- 65
- 67
- 71
6. 등차수열 {an}에 대하여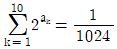 
, 
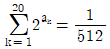일 때, 
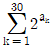의 값은?
- 5/1024
- 3/512
- 7/1024
- 1/128
7. 두 함수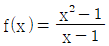 
과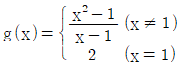 
에 대한 설명으로 가장 옳은 것은?
- 두 함수 모두 x=1에서 연속이다.
- 두 함수 모두 x=1에서 불연속이다.
- x=1에서 f(x)는 연속이고, g(x)는 불연속이다.
- x=1에서 f(x)는 불연속이고, g(x)는 연속이다.
8. 다항식 x22+2x+5를 (x-1)2으로 나누었을 때, 나머지는 ax+b이다. b의 값은?
- -16
- -14
- -12
- -10
9. 점 (0, 2)와 직선 y=-3에서 같은 거리에 있는 점의 자취의 방정식을 f(x)라 하자. 함수 f(x)의 x=5에서 접선의 기울기 값은?
- -2
- 1
- 2
- 3
10. 이차함수 y=ax2-2ax+a+1 (a＞0)의 그래프와 직선 y=k는 서로 다른 두 점에서 만나며 그 두 교점을 각각 A, B라 하고, 주어진 이차함수의 그래프의 꼭짓점을 C라 하자. 세 점 A, B, C를 꼭짓점으로 하는 삼각형이 정삼각형일 때, a(k-1)의 값은?
- 0
- 1
- 2
- 3
11. 다항식 f(x)가 임의의 실수 x에 대하여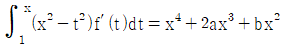 
일 때, 
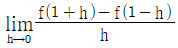의 값은?
- -2
- -1
- 1
- 2
12. 연속확률변수 X는 함숫값을 [0, 12]에서 갖는다. P(a≤X≤b)는 (b-a)에 비례하고, 비례상수를 k라 하자. 이때 옳은 것을 ＜보기＞에서 모두 고른 것은? (단, 0≤a≤b≤12)
- ㄱ
- ㄷ
- ㄱ, ㄴ
- ㄴ, ㄷ
13. 곡선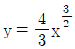 
(0≤x≤2)의 길이는?
- 10/3
- 11/3
- 13/3
- 14/3
14. 확률변수 X가 이항분포 B(n, p)를 따를 때, E(X(X-1))의 값은?
- n2p
- np2
- n2p2
- n(n-1)p2
15. 극한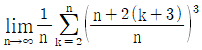 
의 값은?
- 1/4
- 10
- 65/4
- 20
16. 두 수열 {an}, {bn}은 공비가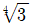 
인 등비수열이고, bn = an + an+1 + 1을 만족한다. 수열 {an}의 첫째항부터 제20항까지의 합이 232일 때, b1의 값은?
17. 실수 t에 대하여 곡선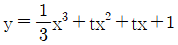 
에 접하는 직선의 기울기가 최소가 될 때, 이 접선의 y절편을 f(t)라고 하자. f′(1)+f(1)의 값은? (단, f′은 f의 도함수이다.)
- 1
- 5/3
- 7/4
- 7/3
18. 이차부등식 x2+2ax+b＜0의 해가 존재하지 않을 때, 실수 a, b에 대하여 a+b의 최솟값은?
19. 두 사건 A, B에 대하여 P(A)=2/5, P(A|B)=1/3, P(Ac∩Bc)=2/5, P(B|A)의 값은? (단, Ac는 A의 여사건이다.)
- 3/20
- 1/5
- 1/4
- 3/10
20. 1부터 3000까지의 자연수 중에서 3000과 서로소인 자연수는 몇 개인가?
- 750
- 800
- 830
- 910