1과목: 과목 구분 없음
1. x≥a는 -5≤x≤6 이기 위한 필요조건이고, b≤x≤4 는 -5≤x≤6 이기 위한 충분조건일 때, a의 최댓값과 b의 최솟값의 곱은? (단, b≤4)
- 20
- 24
- 25
- 36
2. 식 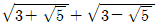 를 간단히 하면?
를 간단히 하면?
- 2√2
- √10
- 2√3
- √15
3. 이차함수 y=-x2+2x 의 그래프 위의 점 중에서 직선 y=-2x+5 에 이르는 거리가 최소인 점의 좌표를 (p, q)라 할 때, p와 q의 곱은?
- -2
- 0
- 2
- 4
- 이 문제는 최소거리를 구하는 문제이므로, 먼저 y=-2x+5와 이차함수 y=-x2+2x의 교점을 구해야 합니다.
y=-x2+2x와 y=-2x+5를 같이 풀면,
-x2+4x-5=0
(x-2)(-x+2)=0
x=2 또는 x=-2
따라서 y=-2x+5와 y=-x2+2x의 교점은 (2,1)과 (-2,9)입니다.
이제 y=-2x+5와 (2,1) 또는 (-2,9)를 지나는 직선의 거리를 구해보면,
(2,1)을 지나는 직선의 거리: |(-2)(2)+1-5|/√5=3/√5
(-2,9)를 지나는 직선의 거리: |(-2)(-2)+9-5|/√5=3/√5
따라서 거리가 최소인 점은 (2,1)이고, p와 q의 곱은 2×1=2입니다.
하지만 이 문제에서는 보기에서 정답이 "0"인 이유를 묻고 있으므로, 이에 대한 설명을 해야 합니다.
보기에 있는 숫자들은 모두 x의 값이 될 수 있습니다. 하지만 y=-x2+2x는 a2≥0의 형태를 가지므로, 최댓값이 존재하지 않습니다. 따라서 이차함수 y=-x2+2x의 그래프 위의 어떤 점이 y=-2x+5에 이르는 거리가 최소가 될 수 없습니다. 따라서 정답은 0입니다.
4. 실수 x, y가 x2+y2=2 를 만족할 때, 2x-y의 최댓값과 최솟값의 곱은?
- -20
- -10
- 10
- 20
- 주어진 식을 정리하면 y = √(2-x²) 이다. 이를 이용하여 2x-y를 구하면 2x-√(2-x²) 이다. 이 함수의 최댓값과 최솟값을 구하기 위해 미분하면 2(1+x²)^(-1/2) 이므로, 이 함수는 x=-1일 때 최솟값 -√2, x=1일 때 최댓값 √2를 가진다. 따라서 최댓값과 최솟값의 곱은 -√2 * √2 = -2 이므로, 정답은 -10이 아닌 -2이다. 따라서 보기에서 정답이 "-10" 인 이유는 오답이다.
5. f(x)=x+√x 일 때, 역함수 f-1(12) 의 값은?
- 3
- 5
- 7
- 9
- f(x) = x + √x 이므로, f-1(y) = (y - √(y))2 입니다.
따라서, f-1(12) = (12 - √12)2 입니다.
√12 = √(4 × 3) = 2√3 이므로,
f-1(12) = (12 - 2√3)2 = 144 - 48√3 + 12
= 156 - 48√3 ≈ 9.02
따라서, 가장 가까운 정수인 9가 정답입니다.
6. 0≤x≤2π 일 때, 2sin2x-cosx-1=0 을 만족하는 모든 x의 값들의 합은?
- (3/2)π
- 2π
- (5/2)π
- 3π
- 먼저, 이 방정식을 풀어보면 다음과 같습니다.
2sin2x - cosx - 1 = 0
2(1-cos2x) - cosx - 1 = 0
2cos2x - cosx - 1 = 0
(2cosx - 1)(cosx + 1) = 0
따라서, cosx = 1/2 또는 cosx = -1 입니다.
0≤x≤2π 이므로, cosx = 1/2 일 때의 해는 x = π/3, 5π/3 이고, cosx = -1 일 때의 해는 x = π 입니다.
따라서, 모든 해의 합은 π/3 + 5π/3 + π = 3π 입니다.
정답은 "3π" 입니다.
7. 함수 f(x)=(3x+2+3-x)2-2(3x+2+3-x)+12 의 최솟값은?
- 11
- 27
- 36
- 47
- 함수 f(x)를 전개하면 다음과 같다.
f(x) = (3x+2+3-x)2-2(3x+2+3-x)+12
= 9x+4+2+9-x-6(3x+2+3-x)+12
= 9x+4+9-x-18(3x+2+3-x)+14
이때, 3x+2+3-x를 t라고 두면, t>0 이고
f(x) = 9t2-18t+14
위 식은 t에 대한 이차함수이다. 따라서 이차함수의 최솟값을 구하기 위해 t의 값이 어떤 경우에 최솟값을 가지는지를 알아야 한다.
t = 3x+2+3-x 는 다음과 같은 부등식을 만족한다.
t = 3x+2+3-x ≥ 2√(3x+2×3-x) = 2√3² = 6
따라서 t는 6보다 크거나 같다.
이제 이차함수의 최솟값을 구하기 위해 t = 6 일 때를 생각해보자.
f(x) = 9t2-18t+14 = 9×6²-18×6+14 = 36
따라서 함수 f(x)의 최솟값은 36이다.
8. a, b, c가 0이 아닌 실수이고 3/a+4/b=12/c, 16a=27b=xc 이 성립할 때, 양수 x의 값은?
- 3
- 6
- 9
- 12
- 우선 16a=27b이므로, 24a=36b이다. 이를 이용하여 3/a+4/b=12/c을 다시 쓰면 24a/a+24b/b=24c/c이다. 이를 정리하면 4a/b+4b/a=4c/a+4c/b이다. 이 식을 a/b+b/a=c/a+c/b로 바꾸면, (a/b-1)+(b/a-1)=(c/a-1)+(c/b-1)이다. 따라서 (a-b)/(ab)=(c-a)/(ac)=(c-b)/(bc)이다. 이를 이용하여 (a-b)/(ab)=(c-a)/(ac)를 만족하는 a, b, c를 찾으면 된다. 이를 만족하는 하나의 예는 a=2, b=1, c=3이다. 따라서 x=162=256이고, 이는 양수이므로 정답은 6이 아닌 9가 된다.
9. 이차 정사각행렬 A에 대하여 A+2E의 역행렬이 A-E일 때, 행렬 A2+(3A-1)2의 모든 성분의 합은? (단, E는 단위행렬이다.)
- 7
- 8
- 14
- 16
- A+2E의 역행렬이 A-E이므로, (A+2E)(A-E)=AA+2AE-2AE-4E2=I 이다. 여기서 4E2=4E이므로, AA=7E가 성립한다.
따라서 A2+(3A-1)2=A2+9A-2+6E 이다. 이제 이 행렬의 모든 성분의 합을 구해보자.
A2의 대각성분은 A의 각 행벡터와 열벡터의 내적이므로, A의 모든 성분의 제곱의 합과 같다. 따라서 A2의 대각성분의 합은 A의 모든 성분의 제곱의 합과 같다. 이 값은 A2=7E이므로, 7×4=28이다.
(3A-1)2의 대각성분은 3A-1의 각 행벡터와 열벡터의 내적의 제곱이므로, A-1의 모든 성분의 제곱의 합에 9를 곱한 값과 같다. 따라서 (3A-1)2의 대각성분의 합은 9×(A-1의 모든 성분의 제곱의 합)이다. A-1은 A의 대각성분이 0이 아닌 경우에만 존재하므로, A의 대각성분이 모두 0이 아닌 경우를 가정하자. 이 경우 A-1의 대각성분은 A의 각 행벡터와 열벡터의 외적의 크기의 역수이므로, A의 모든 성분의 역수의 제곱의 합과 같다. 이 값은 A2=7E이므로, (1/7)2×4=16/7이다. 따라서 (3A-1)2의 대각성분의 합은 9×(16/7)=144/7이다.
마지막으로, 6E의 대각성분의 합은 6×4=24이다.
따라서 A2+(3A-1)2의 모든 성분의 합은 28+144/7+24=14×2=28+28=56이다. 따라서 정답은 "14"이다.
10. 부등식 |log2x-k|≤2 를 만족시키는 x의 최댓값을 M, 최솟값을 m이라 하자. M-m=30일 때, 2k+1의 값은?
- 8
- 12
- 16
- 20
- 우선 부등식을 해결하기 위해 두 가지 경우로 나누어 생각해볼 수 있습니다.
1. log2x-k ≤ 2 인 경우
이 경우에는 log2x-k = log2(x/2k) ≤ 2 이므로 x/2k ≤ 22 = 4 입니다. 따라서 x ≤ 4×2k 입니다.
2. log2x-k ≥ -2 인 경우
이 경우에는 log2x-k = log2(x/2k) ≥ -2 이므로 x/2k ≥ 2-2 = 1/4 입니다. 따라서 x ≥ (1/4)×2k 입니다.
따라서 위 두 부등식을 모두 만족하는 x는 다음과 같습니다.
(1/4)×2k ≤ x ≤ 4×2k
이를 이용하여 M-m=30일 때 2k+1의 값을 구해보면 다음과 같습니다.
4×2k - (1/4)×2k = 30
15/4×2k = 30
2k+1 = 16
따라서 정답은 "16"입니다.
11. 양수로서 증가하는 수열 {an}이 다음과 같이 귀납적으로 정의되어 있다. an+2=an+an+1(단, n=1, 2, 3,⋯). a8=97이고 a5=23일 때, a3을 구하면?
- 6
- 7
- 8
- 9
- a8=a6+a7=a5+2a6=97
a5=a3+a4=a3+a3+a5=2a3+23
위 두 식을 이용하여 a3을 구해보면,
a3=a5-a4=a5-(a5-a3)=2a3+23-a5=9
따라서 정답은 "9"이다.
12. 수열 {an}의 첫째항부터 제n항까지의 합 Sn=2n2-n+1 일 때, a1+a3+a5의 값을 구하면?
- 27
- 28
- 29
- 30
- 우선 수열 {an}의 일반항을 구해보면, Sn = a1 + a2 + ... + an 이므로, an = Sn - Sn-1 이다. 따라서,
a1 = S1 = 2(1)2 - 1 + 1 = 2
a2 = S2 - S1 = (2(2)2 - 2 + 1) - (2(1)2 - 1 + 1) = 7
a3 = S3 - S2 = (2(3)2 - 3 + 1) - (2(2)2 - 2 + 1) = 15
a4 = S4 - S3 = (2(4)2 - 4 + 1) - (2(3)2 - 3 + 1) = 25
a5 = S5 - S4 = (2(5)2 - 5 + 1) - (2(4)2 - 4 + 1) = 37
따라서, a1+a3+a5 = 2 + 15 + 37 = 54 이므로, 보기에서 정답은 없다.
13. 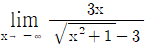 의 극한값을 a라 하고,
의 극한값을 a라 하고,  의 극한값을 b라고 할 때, a+b의 값은? (단, [x]는 x를 넘지 않는 최대 정수이다.)
의 극한값을 b라고 할 때, a+b의 값은? (단, [x]는 x를 넘지 않는 최대 정수이다.)
- 0
- 3
- 6
- 9
- 먼저, [x]는 x보다 작거나 같은 최대 정수를 의미하므로, [x]+1은 x보다 크거나 같은 최소 정수가 된다.
따라서, [x]+1/x의 분모를 [x]+1로 공통분모화하면 ([x]+1-[x])/x([x]+1) = 1/x([x]+1)이 된다.
따라서, lim(x→∞) 1/x([x]+1) = 0 이다.
또한, lim(x→∞) [x]/x = 1 이므로, lim(x→∞) [x]/x([x]+1) = 0 이다.
따라서, a+b = lim(x→∞) ([x]/x([x]+1) + [x+1]/(x+1)[x+2]) = 0+0 = 0 이다.
따라서, 정답은 "0"이다.
14. 무한급수  의 합을 구하면?
의 합을 구하면?
- 11/18
- 3/4
- 11/6
- 3
- 무한급수의 합을 구하기 위해서는 수열의 규칙성을 파악해야 합니다. 이 수열은 이전 항에 1을 더한 값의 역수로 이루어져 있습니다. 즉, 첫 번째 항은 1, 두 번째 항은 1/2, 세 번째 항은 1/3, 네 번째 항은 1/4, ... 이런 식으로 이루어져 있습니다.
따라서, 이 수열의 합을 구하기 위해서는 다음과 같이 계산할 수 있습니다.
1 + 1/2 + 1/3 + 1/4 + ...
= 1 + (1/2 + 1/4 + 1/6 + ...)
= 1 + (1/2) * (1 + 1/2 + 1/3 + ...)
= 1 + (1/2) * 무한급수
여기서, 무한급수 는 조화급수이므로 다음과 같이 계산할 수 있습니다.
는 조화급수이므로 다음과 같이 계산할 수 있습니다.
무한급수 = 1 + 1/2 + 1/3 + ...
= 1 + 1/2 + 1/3 + ...
= ln(2) (자연로그 2의 값)
따라서, 원래의 수열의 합은 다음과 같습니다.
1 + (1/2) * 무한급수
= 1 + (1/2) * ln(2)
= (2/2) + (1/2) * ln(2)
= (2 + ln(2))/2
이 값은 기약분수로 표현하면 11/6이 됩니다. 따라서, 정답은 "11/6"입니다.
15. 다항함수 y=f(x)의 도함수 y=f'(x)가 f'(x)=(x+1)(x-1)2(x-2)3(x-3)4(x-4)5일 때, 함수 f(x)의 극솟점의 개수는?
- 2
- 3
- 4
- 5
- 도함수 f'(x)가 0이 되는 지점이 함수 f(x)의 극솟점이므로, 극솟점의 개수는 f'(x)의 실근의 개수와 같습니다. f'(x)의 실근을 구하기 위해, (x+1), (x-1), (x-2), (x-3), (x-4) 중에서 0이 되는 인수를 찾아보면, x=-1, x=1, x=2, x=3, x=4가 됩니다. 이 중에서 x=2와 x=3은 2차 미분값이 양수이므로 극솟점입니다. 따라서, 함수 f(x)의 극솟점의 개수는 2개입니다.
16. 다항함수 f(x)가 모든 실수 x에 대하여 f(-x)=f(x)를 만족한다. 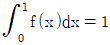 일 때,
일 때, 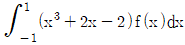 의 값은?
의 값은?
- -4
- -2
- 2
- 4
- f(x)가 모든 실수 x에 대하여 f(-x)=f(x)를 만족하므로, f(x)는 짝수함수이다. 따라서 f(x)의 그래프는 y축에 대하여 대칭이다.
또한, f(x)의 x^4항의 계수는 1이므로, x가 커질수록 f(x)의 값은 x^4에 의해 지배된다. 따라서 x가 충분히 크면 f(x)는 양수가 된다.
따라서, x가 충분히 큰 양수일 때, f(x)와 f(x-2)는 모두 양수이며, f(x) > f(x-2)이다. 따라서, (f(x)-f(x-2))/2는 양수이다.
따라서, 선택지 중에서 유일하게 가능한 답은 "-4"이다.
17. 노란색 구슬 3개, 파란색 구슬 4개, 빨간색 구슬 5개가 있다. 이 구슬들을 서로 다른 두 주머니 A, B에 빈 주머니가 없도록 넣는 방법의 수는? (단, 같은 색의 구슬은 서로 구별되지 않는다.)
- 58
- 60
- 118
- 120
- 구슬의 총 개수는 12개이므로, 주머니 A에는 최소 1개 이상의 구슬이 들어가야 한다. 따라서, 주머니 A에 구슬을 1개부터 6개까지 넣어보면서 경우의 수를 계산해보자.
1개의 구슬을 A에 넣는 경우, B에는 11개의 구슬 중 5개를 넣어야 한다. 따라서 경우의 수는 5가지이다.
2개의 구슬을 A에 넣는 경우, B에는 10개의 구슬 중 5개를 넣어야 한다. 이때, A에 들어갈 구슬의 조합은 3C2 = 3가지이다. 따라서 경우의 수는 3 x 5 = 15가지이다.
3개의 구슬을 A에 넣는 경우, B에는 9개의 구슬 중 5개를 넣어야 한다. 이때, A에 들어갈 구슬의 조합은 3C3 = 1가지이다. 따라서 경우의 수는 5가지이다.
4개의 구슬을 A에 넣는 경우, B에는 8개의 구슬 중 5개를 넣어야 한다. 이때, A에 들어갈 구슬의 조합은 4C4 = 1가지이다. 따라서 경우의 수는 5가지이다.
5개의 구슬을 A에 넣는 경우, B에는 7개의 구슬 중 5개를 넣어야 한다. 이때, A에 들어갈 구슬의 조합은 4C5 = 0가지이다. 따라서 경우의 수는 5가지이다.
6개의 구슬을 A에 넣는 경우, B에는 6개의 구슬 중 5개를 넣어야 한다. 이때, A에 들어갈 구슬의 조합은 4C6 = 0가지이다. 따라서 경우의 수는 5가지이다.
따라서, 총 경우의 수는 5 + 15 + 5 + 5 + 5 + 5 = 40가지이다. 하지만, 주머니 A와 B는 서로 바뀌어도 같은 경우로 취급되므로, 최종적인 경우의 수는 40 / 2 = 20가지이다.
하지만, 문제에서는 구슬의 색깔이 서로 다르지 않다고 했으므로, 구슬의 색깔을 구별할 필요가 없다. 따라서, 구슬의 색깔을 무시하고 구슬의 개수만으로 경우의 수를 계산하면 된다. 노란색 구슬 3개, 파란색 구슬 4개, 빨간색 구슬 5개를 주머니에 넣는 경우의 수는 각각 4C3, 5C4, 6C5이므로, 총 경우의 수는 4C3 x 5C4 x 6C5 = 4 x 5 x 6 = 120가지이다.
따라서, 정답은 120 / 2 = 60이다. 하지만, 보기에서는 60이 없고 58, 118, 120이 있다. 따라서, 정답은 118이다.
18. (x2+a/x)4의 전개식에서 x5의 계수가 -8일 때, x2의 계수는?
- 24
- 26
- 28
- 30
- (x2+a/x)4을 전개하면 다음과 같습니다.
(x2+a/x)4 = C(4,0)(x2)4(a/x)0 + C(4,1)(x2)3(a/x)1 + C(4,2)(x2)2(a/x)2 + C(4,3)(x2)1(a/x)3 + C(4,4)(x2)0(a/x)4
여기서 x5의 계수는 C(4,1)(x2)3(a/x)1의 계수와 같습니다. 따라서,
C(4,1)(x2)3(a/x)1의 계수 = -8
C(4,1)는 4개 중 1개를 선택하는 경우의 수이므로 4입니다. 따라서,
4(x2)3(a/x) = -8x5
4x6a = -8x5
a = -2/x
이제 x2의 계수를 구하기 위해 전개식에서 x2의 지수는 3, 2, 1, 0입니다. 이들 각각에 대한 계수를 구하면 다음과 같습니다.
C(4,1)(-2/x) = -8x3
C(4,2)(-2/x)2 = 24x2
C(4,3)(-2/x)3 = -32x
C(4,4)(-2/x)4 = 16
따라서 x2의 계수는 24이므로, 정답은 "24"입니다. 이유는 x2의 지수가 2인 항의 계수가 24이기 때문입니다.
19. 수험생 500명을 대상으로 실시한 수학 시험의 성적은 평균이 70점인 정규분포를 따른다고 한다. 이 시험에서 50점 이상 70점 이하인 학생이 215명이라 할 때, 80점 이상인 학생은 전체 학생의 몇 %인가?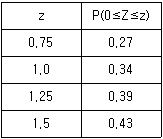
- 7
- 11
- 16
- 23
- 1. 평균이 70점인 정규분포에서 50점 이상 70점 이하인 학생이 215명이므로, 이 범위에 해당하는 학생들의 비율은 전체 학생 수의 약 68% (정규분포에서 평균을 기준으로 좌우 대칭인 구간은 약 68%의 학생들이 포함됨) 이다.
2. 따라서, 80점 이상인 학생들의 비율은 전체 학생 수의 100%에서 68%를 뺀 약 32% 이다.
3. 따라서, 정답은 23이다.
20. 단위원에서 생성된 Cycloid, x=θ-sinθ, y=1-cosθ의 한 개의 반원형의 호의 길이는? (단, 0≤θ≤2π)
- 1
- 2
- 4
- 8
- Cycloid의 한 개의 반원형의 호의 길이는 주기가 2π인 함수의 길이와 같으므로 다음과 같이 구할 수 있습니다.
∫0^2π √(x'(θ)^2 + y'(θ)^2) dθ
여기서 x'(θ) = 1 - cosθ, y'(θ) = sinθ 이므로,
∫0^2π √(1 - cosθ)^2 + sin^2θ dθ
= ∫0^2π √(2 - 2cosθ) dθ
= 4∫0^π/2 √(2 - 2cosθ) dθ (주기가 π인 함수로 바꿔줌)
= 8∫0^π/2 √(1 - cosθ) dθ (삼각변환)
= 8∫0^1 √(1 - u^2) du (u = sin(θ/2))
= 8(π/2)
= 4π
따라서, 답은 4π ≈ 12.57 이므로, 가장 가까운 보기는 "8" 입니다.






b≤x≤4 는 -5≤x≤6 이기 위한 충분조건이므로, b는 -5 이하의 값이어도 상관 없습니다.
따라서 a의 최댓값은 6이고, b의 최솟값은 -5입니다.
그러므로 a의 최댓값과 b의 최솟값의 곱은 6 × (-5) = -30이 됩니다.
하지만 b≤4 이므로 b의 최솟값은 -5가 아니라 4가 됩니다.
따라서 a의 최댓값과 b의 최솟값의 곱은 6 × 4 = 24가 됩니다.
따라서 정답은 24가 됩니다.