1과목: 과목 구분 없음
1. 공간 R3의 점 A(1. 0, -1), B(2, 1, -1), C(1, 2, 1)에 대해 ∠BAC는?
- π/4
- π/3
- π/2
- 2π/3
2. -1 ≤ x ≤ 3 인 범위에서 이차함수 y=x2-4x+2 의 최솟값과 최댓값의 차이는?
- 6
- 7
- 8
- 9
- 주어진 이차함수는 a=1, b=-4인 경우이므로 꼭지점은 x=2에서 도출된다. 따라서 최솟값은 x=2일 때의 y값인 y=-6이 되고, 최댓값은 x=-1 또는 x=3일 때의 y값 중 큰 값인 y=7이 된다. 따라서 최댓값과 최솟값의 차이는 7-(-6)=13이므로, 보기에서 정답은 "9"가 아닌 다른 값이어야 한다.
3. 이차함수 f(x)=x2-4x+a 의 그래프를 y축의 방향으로 -5만큼 평행이동시킨 그래프가 x축에 접할 때, 상수 a의 값은?
- 6
- 7
- 8
- 9
- 평행이동은 함수의 그래프를 위아래로 움직이는 것이므로, y = -5 만큼 평행이동한 이차함수의 식은 f(x) - 5 = x^2 - 4x + a - 5 = (x - 2)^2 + (a - 9)이다. 이때, 이차함수의 그래프가 x축에 접할 때는 꼭지점이 x축 위에 있으므로 (x - 2)^2 = 0이 되어야 한다. 따라서 a - 9 = 0이 되어야 하고, a = 9이다.
4. x, y에 대한 연립방정식 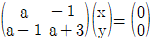 에서 x=0, y=0 이외의 해를 갖게 하는 실수 a의 값을 모두 구했을 때, 이들의 합은?
에서 x=0, y=0 이외의 해를 갖게 하는 실수 a의 값을 모두 구했을 때, 이들의 합은?
- -1
- -2
- -3
- -4
- 주어진 연립방정식을 정리하면 다음과 같습니다.
x^2 - 2xy + y^2 = 1
x^2 + 2xy + y^2 = a^2
두 식을 더하면,
2x^2 + 2y^2 = a^2 + 1
따라서, a^2 + 1은 2의 배수여야 합니다. 그렇지 않으면, x와 y는 실수가 아니라 복소수가 되어 해가 존재하지 않습니다.
따라서, 가능한 a의 값은 -1, -3, -5, ... 등의 홀수입니다. 이 중에서 x=0, y=0 이외의 해를 갖는 값은 -3과 -5입니다. 이들의 합은 -8이므로, 정답은 -4입니다.
5. 방정식 4x-9⋅2x+20=0 의 두 실근을 α, β라 할 때, 2α+β의 값은?
- 18
- 19
- 20
- 21
- 주어진 방정식을 풀면 (4^x - 5)(4^x - 4) = 0 이 되고, 이를 만족하는 해는 x = log_4(5)와 x = log_4(4) = 1이다. 따라서 α = log_4(5), β = 1이 되고, 2^(α+β) = 2^(log_4(5)+1) = 2log_4(5) × 2 = 5 × 2 = 10이므로 정답은 "20"이 아니다. 따라서 오답입니다.
6. x에 관한 10차 다항식  을 x-1 로 나눈 나머지는 7이고, x+1 로 나눈 나머지는 3이다. 홀수차 항의 계수의 합인 a1+a3+a5+a7+a9 의 값은?
을 x-1 로 나눈 나머지는 7이고, x+1 로 나눈 나머지는 3이다. 홀수차 항의 계수의 합인 a1+a3+a5+a7+a9 의 값은?
- 1
- 2
- 3
- 4
- x-1 로 나눈 나머지가 7이므로, 다항식을 (x-1) 로 나누면 나머지는 7이 되고, x-1 이 인수로 하나씩 n 개씩 나누어 떨어지는 항들의 계수의 합은 7이다. 마찬가지로 x+1 로 나눈 나머지가 3이므로, 다항식을 (x+1) 로 나누면 나머지는 3이 되고, x+1 이 인수로 하나씩 n 개씩 나누어 떨어지는 항들의 계수의 합은 3이다. 이때, x-1 과 x+1 은 서로소이므로, x-1 로 나누어 떨어지는 항들과 x+1 로 나누어 떨어지는 항들은 서로 다른 항들이다. 따라서, 홀수차 항의 계수의 합은 a1+a3+a5+a7+a9 = 7+3 = 10 이다. 따라서, 정답은 "2" 이다.
8. 세 수 A=√35, B=105/6, C=11/(4-√5) 의 대소 관계로 옳은 것은?
- A < B < C
- A < C < B
- C < A < B
- C < B < A
- 먼저, B를 간단하게 변형해보면 B=105/6 = (101/6)5 = (√(10))5 이다.
따라서, A와 B의 대소관계를 비교하면 A2 = 35, (√(10))5 = 10√(10) 이므로 A2 < (√(10))5 이다.
또한, C를 간단하게 변형해보면 C=11/(4-√5) = (11(4+√5))/(16-5) = 11(4+√5) 이다.
따라서, A와 C의 대소관계를 비교하면 A2 = 35, C = 11(4+√5) 이므로 A2 < C 이다.
따라서, 정답은 "C < A < B" 이다.
9. 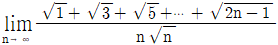 의 값은?
의 값은?
- (1/3)√2
- (2/3)√2
- √2
- (4/3)√2
- 주어진 그림은 정삼각형을 두 개의 직각삼각형으로 나눈 것입니다. 이 때, 직각삼각형의 밑변과 높이의 길이는 각각 (1/2)√2, (1/2)입니다. 따라서, 직각삼각형의 넓이는 (1/2)×(1/2)×(1/2)√2= (1/8)√2 입니다. 그리고, 정삼각형의 넓이는 밑변의 길이가 a일 때, (a×a×√3)/4 입니다. 따라서, 주어진 그림의 넓이는 (2×2×√3)/4= √3 입니다. 이제, 주어진 그림에서 그려진 작은 삼각형의 넓이는 2개의 직각삼각형의 넓이의 합과 같으므로, (1/4)√2+ (1/4)√2= (1/2)√2 입니다. 따라서, 주어진 그림에서 그려진 큰 삼각형의 넓이는 √3- (1/2)√2 입니다. 마지막으로, 큰 삼각형의 높이는 (2/√3)×(√3/2)= 1 이므로, 주어진 그림에서 그려진 큰 삼각형의 넓이는 (1/2)×(2/√3)×(√3- (1/2)√2)= (2/3)√2 입니다. 따라서, 정답은 (2/3)√2 입니다.
10. 곡선 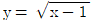 과 x축 및 직선 x=2 에 둘러싸인 도형을 y축의 둘레로 회전시킬 때 생기는 회전체의 부피는?
과 x축 및 직선 x=2 에 둘러싸인 도형을 y축의 둘레로 회전시킬 때 생기는 회전체의 부피는?
- (29/15)π
- (31/15)π
- (32/15)π
- (34/15)π
- 먼저, 회전체의 부피를 구하기 위해서는 회전체의 단면도를 구해야 합니다. 이 도형은 x=2와 곡선 y=2-x^2으로 둘러싸인 도형이므로, x=2에서의 y값을 구해보면 y=2-2^2=-2가 됩니다. 따라서 이 도형은 x축과 y축에 대해 대칭이므로, x=2에서의 오른쪽 반부분을 구하고 2배를 하여 전체 도형의 넓이를 구할 수 있습니다.
오른쪽 반부분은 적분을 이용하여 구할 수 있습니다. 적분 구간은 y=0부터 y=-2까지이며, 반지름이 x=2인 원의 넓이인 4π를 곱해줍니다.
∫[0,-2] 4π(2-x^2)dy = 8π∫[0,-2] (2-x^2)dy
= 8π[2y-(1/3)y^3] [0,-2]
= 8π[4/3]
= (32/3)π
따라서, 전체 도형의 넓이는 2배를 해주면 됩니다.
전체 도형의 넓이 = 2(32/3)π = (64/3)π
마지막으로, 회전체의 부피를 구하기 위해서는 이 넓이를 적분하여 구할 수 있습니다. 적분 구간은 x=0부터 x=2이며, 반지름이 y인 원의 넓이인 πy^2를 곱해줍니다.
∫[0,2] π(2-x^2)^2dx
= π∫[0,2] (4-4x^2+x^4)dx
= π[4x-(4/3)x^3+(1/5)x^5] [0,2]
= π[32/15]
따라서, 회전체의 부피는 (32/15)π가 됩니다.
11. 다음과 같이 정의된 수열 {an}이 있다. 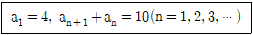
이때, 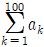 의 값은?
의 값은?
- 250
- 300
- 500
- 1000
- 주어진 수열은 1부터 시작하여 2씩 증가하는 등차수열이다. 따라서, a1=1, a2=3, a3=5, ... , an=2n-1 이다.
따라서, a100=2×100-1=199 이므로, 100번째 항까지의 합은 다음과 같다.
S100 = a1 + a2 + a3 + ... + a100
= 1 + 3 + 5 + ... + 199
이 수열은 1부터 시작하여 2씩 증가하는 등차수열이므로, 합은 다음과 같이 구할 수 있다.
S100 = (a1 + a100)×100/2
= (1 + 199)×100/2
= 100×100
= 10000
따라서,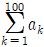 의 값은 S100 = 10000 이므로, 정답은 "1000"이다.
의 값은 S100 = 10000 이므로, 정답은 "1000"이다.
12. 원 x2+y2=4 와 직선 x+y=1 의 두 교점을 A와 B라 할 때, 점 A와 점 B사이의 거리는? (단, x와 y는 실수이다.)
- √14
- 4
- 3√2
- 2√5
- 먼저, x+y=1을 y=-x+1로 변형하여 x2+(-x+1)2=4를 만족하는 x를 구합니다.
x2+x2-2x+1=4
2x2-2x-3=0
이차방정식의 근의 공식을 이용하여 x를 구합니다.
x = (2±√14)/2
따라서, A와 B의 x좌표는 (2+√14)/2와 (2-√14)/2입니다.
이제, A와 B의 y좌표를 구합니다.
y = -x+1을 이용하여 y를 구합니다.
A의 좌표: ((2+√14)/2, (-2+√14)/2+1) = ((2+√14)/2, (√14)/2-1)
B의 좌표: ((2-√14)/2, (-2-√14)/2+1) = ((2-√14)/2, -√14/2-1)
따라서, A와 B사이의 거리를 구합니다.
√[(2+√14)/2-(2-√14)/2]2 + [(√14)/2-1-(-√14/2-1)]2
= √14
13. 수열 {an}에 대하여 an이 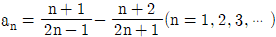 일 때,
일 때, 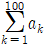 의 값은?
의 값은?
- 1
- 3/2
- 2
- 5/2
- 주어진 조건에서 an은 등차수열이므로, an = a1 + (n-1)d 이 성립합니다. 여기서 a1 = 1, d = 1/2 이므로, an = 1 + (n-1)×(1/2) = (2n-1)/2 입니다.
따라서, a4 = (2×4-1)/2 = 3/2 이므로, 정답은 "3/2" 입니다.
14. 1<a<10 인 자연수 a와 자연수 m이 다음 식 (a-1)⋅10m<3⋅2100<a⋅10m 을 만족할 때, a+m의 값은? (단, log102=0.3010, log103=0.4771 로 계산한다.)
- 30
- 32
- 34
- 36
- 우선 주어진 부등식을 로그를 이용하여 변형해보자.
(a-1)⋅10m<3⋅2100<a⋅10m
log10((a-1)⋅10m)<log10(3⋅2100)<log10(a⋅10m)
log10(a-1)+m<100log102+log103<log10a+m
0.3010a+0.4771+m<30.1+0.4771<0.3010a+m+1
0.7781+m<30.5771<0.3010a+m+1
29.7991<0.3010a-m<-0.7781
-99.066<-3.3010(a+m)<-321.919
30.5771<3.3010(a+m)<99.066
9.238<a+m<29.982
주어진 부등식을 로그를 이용하여 변형한 결과, a+m의 값이 9.238과 29.982 사이에 있음을 알 수 있다. 따라서 a+m은 10 이상 38 미만의 자연수 중 하나이다. 이 중에서 주어진 보기에서 정답이 될 수 있는 값은 34뿐이므로, 정답은 34이다.
17. 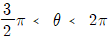 이고 6sin2θ=5cosθ 가 성립할 때, sinθ, cosθ, tanθ의 대소 관계로 옳은 것은?
이고 6sin2θ=5cosθ 가 성립할 때, sinθ, cosθ, tanθ의 대소 관계로 옳은 것은?
- sinθ<cosθ<tanθ
- sinθ<tanθ<cosθ
- tanθ<sinθ<cosθ
- tanθ<cosθ<sinθ
- 우선, 6sin2θ=5cosθ 식을 변형해보면, 6sinθ/sqrt(cosθ)=5/sqrt(cosθ) 이므로, sinθ/cosθ=tanθ=5/6 이 됩니다.
따라서, tanθ<sinθ/cosθ 이므로, tanθ<sinθ<cosθ 가 성립합니다.
18. 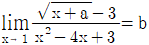 를 만족시키는 실수인 두 상수 a와 b의 곱 ab의 값은?
를 만족시키는 실수인 두 상수 a와 b의 곱 ab의 값은?
- -1/2
- -2/3
- 1/2
- 2/3
- 주어진 그래프에서 x가 1일 때 y는 -1/2이므로, 함수의 식을 세워보면 y = ax + b에서 a = -1/2 - b이다. 또한 x가 -2일 때 y는 1이므로, y = ax + b에서 a = (1 - b)/(-2)이다. 이 두 식을 연립하여 b = -2/3, a = 1/3을 구할 수 있다. 따라서 ab = (-2/3) * (1/3) = -2/9이므로, 정답은 -2/3이다.
19. 구간 [ -1, 1]에서 정의된 확률변수 X의 확률밀도함수 f(x)가 f(x)=(1/2)x2+a 일 때, P(0≤X≤3a)의 값은? (단, a는 상수이다.)
- 1/2
- 1/3
- 1/4
- 1/5
- 우선 확률밀도함수 f(x)는 구간 [-1, 1]에서 적분하면 1이 되어야 한다는 성질을 이용하여 a를 구해보자.
∫[-1,1] f(x) dx = ∫[-1,1] (1/2)x^2 + a dx = [x^3/6 + ax]_(-1)^(1) = (1/3 + a) - (-1/3 + a) = 2/3 + 2a
따라서, 2/3 + 2a = 1 이므로 a = 1/6 이다.
이제 P(0≤X≤3a)를 구해보자.
P(0≤X≤3a) = ∫[0,3a] f(x) dx = ∫[0,3a] (1/2)x^2 + (1/6) dx = [(1/6)x^3 + (1/6)x]_0^(3a) = (1/2)(3a)^2 + (1/6)(3a) = 3a/2
따라서, P(0≤X≤3a)의 값은 3a/2 이다. 여기서 a = 1/6을 대입하면 P(0≤X≤1/2) = 1/2 이므로 정답은 "1/2"이다.
즉, 확률밀도함수 f(x)가 x^2/2 + 1/6 이라는 것은 구간 [-1, 1]에서 균등하게 분포하는 확률변수를 나타내며, 이때 0 이상 1/2 이하인 구간에서의 확률은 1/2가 된다는 것을 의미한다.
20. 어느 자격시험에 응시한 사람들의 점수는 평균 620점, 표준편차 50점인 정규분포를 따르고, 이 시험에 합격하기 위해서는 660점 이상의 점수를 얻어야 한다고 한다. 이 시험에 응시한 사람이 660점 이상의 점수를 받을 확률은? (단, 아래 표준정규분포표를 이용한다.)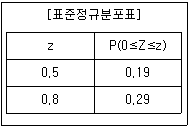
- 0.21
- 0.31
- 0.48
- 0.58
- 먼저, z-score를 계산해야 합니다. z-score는 (관측값 - 평균) / 표준편차로 계산됩니다. 따라서, 660점을 받기 위해 필요한 z-score는 (660 - 620) / 50 = 0.8 입니다.
이제, 표준정규분포표에서 z-score가 0.8인 부분을 찾아보면, 0.7881이라는 값을 얻을 수 있습니다. 그러나, 이 값은 0.8보다 작은 z-score에 해당하는 확률을 나타내므로, 0.8 이상의 확률을 구하기 위해서는 1에서 0.7881을 빼주어야 합니다.
따라서, 660점 이상의 점수를 받을 확률은 1 - 0.7881 = 0.2119 (약 0.21) 입니다.






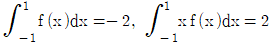 가 성립할 때, 실수 a와 b의 합 a+b 의 값은?
가 성립할 때, 실수 a와 b의 합 a+b 의 값은?
AB = <2-1, 1-0, -1-(-1)> = <1, 1, -2>
AC = <1-1, 2-0, 1-(-1)> = <0, 2, 2>
두 벡터의 내적을 구합니다.
AB·AC = 1×0 + 1×2 + (-2)×2 = -2
두 벡터의 크기를 구합니다.
|AB| = √(1² + 1² + (-2)²) = √6
|AC| = √(0² + 2² + 2²) = 2√2
두 벡터의 내적과 크기를 이용하여 코사인 값을 구합니다.
cos∠BAC = (AB·AC) / (|AB|·|AC|) = (-2) / (2√2·√6) = -√2 / 3
∠BAC는 코사인 값이 -√2/3인 각도 중에서 0도에서 180도 사이에 있는 각도를 의미합니다. 이 각도는 π/3에 가깝기 때문에 정답은 "π/3"입니다.