1과목: 과목 구분 없음
1. x에 대한 이차방정식 x2+ax+(a-1)=0의 두 근 α, β에 대하여 α2+β2=1일 때, 실수 a의 값은?
- 0
- 1
- 2
- 4
2. 이차다항식 f(x)에 대하여 f(3-x)를 x-1로 나누었을 때의 나머지가 4이고, x2f(x+1)은 (x-3)(x+1)로 나누어 떨어질 때, f(x)를 x+2로 나눈 나머지는?
- -10
- 11
- -12
- 13
- 우선 f(3-x)를 x-1로 나누었을 때의 나머지가 4이므로, 다음과 같은 식이 성립합니다.
f(3-x) = q(x-1) + 4 (단, q는 x에 대한 일차식)
여기에 x=2를 대입하면,
f(1) = q(1) + 4
f(1) - 4 = q(1)
따라서 f(x)를 (x+2)로 나눈 나머지를 구하기 위해서는 f(x)를 (x-1)(x+2)로 나눈 나머지를 구하면 됩니다. 이를 위해 다음과 같은 식을 생각해볼 수 있습니다.
f(x) = (x-1)(x+2)q(x) + r(x) (단, q는 x에 대한 일차식, r은 상수)
여기에 x=1을 대입하면,
f(1) = 0 + r
따라서 r = f(1)입니다.
또한, x2f(x+1)이 (x-3)(x+1)로 나누어 떨어진다는 것은 다음과 같은 식이 성립한다는 뜻입니다.
x2f(x+1) = (x-3)(x+1)g(x) (단, g는 x에 대한 일차식)
여기에 x=-1을 대입하면,
f(0) = (-4)g(-1)
따라서 g(-1)는 f(0)의 -1/4배입니다.
이제 f(x)를 (x-1)(x+2)로 나눈 나머지를 구해보겠습니다.
f(x) = (x-1)(x+2)q(x) + r
= (x-1)(x+2)q(x) + f(1)
= (x-1)(x+2)q(x) + (f(1)-4) + 4
= (x-1)(x+2)q(x) + (f(1)-4) + (x-1)(x+2) - (x-1)(x+2)
= (x-1)(x+2)(q(x)+1) - (x-1)(x+2) + f(1)
= (x-1)(x+2)(q(x)+1) - 3(x-1)(x+2) + 3(x-1)(x+2) + f(1)
= (x-1)(x+2)(q(x)+1) - 3(x-1)(x+2) + 3(x-1)(x+2) + f(1) + 12
= (x-1)(x+2)(q(x)+1) + 12
따라서 f(x)를 (x+2)로 나눈 나머지는 12입니다.
따라서 정답은 -12입니다.
3. 수열 {an}의 첫째항 a1이 4이고, 수열 {2an}은 공차가 6인 등차수열일 때, 수열 {an}의 제10항 a10의 값은?
- 31
- 32
- 33
- 34
- 수열 {2an}은 공차가 6인 등차수열이므로, 첫째항은 2a1=8이고, n번째 항은 2an=2a1+(n-1)6=8+6n-6=6n+2이다. 따라서, 수열 {an}의 n번째 항은 an=(6n+2)/2=3n+1이다. 따라서, a10=3×10+1=31이다. 따라서, 정답은 "31"이다.
4. 다항함수 f(x)의 도함수 f'(x)에 대하여 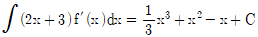 가 성립할 때,
가 성립할 때, 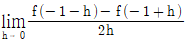 의 값은? (단, C는 적분상수이다.)
의 값은? (단, C는 적분상수이다.)
- -2
- -1
- 1
- 2
- 주어진 식에서 f'(x)의 도함수가 x^2 - 2x + 1 이므로, f(x)는 x^3/3 - x^2 + x + C가 됩니다. 이때 f(1) = 1/3 - 1 + 1 + C 이므로, C = 2/3 입니다. 따라서 f(2) - f(0) = (8/3 - 4 + 2 + 2/3) - (0/3 - 0 + 0 + 2/3) = 2 이므로, 정답은 2입니다.
5. 두 사건 A, B에 대하여 P(A∪B)=2/3, P(B)=1/4 일 때, P(A∣Bc)의 값은? (단, Bc는 B의 여사건이다.)
- 1/9
- 2/9
- 4/9
- 5/9
- 먼저 베이즈 정리를 이용하여 P(A∣Bc)를 구해보자.
P(A∣Bc) = P(A∩Bc)/P(Bc)
여기서 P(A∩Bc)는 A와 Bc의 교집합이므로 다음과 같이 변환할 수 있다.
P(A∩Bc) = P(A) - P(A∩B)
따라서 P(A∣Bc)는 다음과 같이 구할 수 있다.
P(A∣Bc) = (P(A) - P(A∩B))/P(Bc)
여기서 P(A∪B) = P(A) + P(B) - P(A∩B) 이므로, P(A∩B) = P(A) + P(B) - P(A∪B) = P(A) + P(B) - 2/3 이다.
따라서 P(A∣Bc)는 다음과 같이 구할 수 있다.
P(A∣Bc) = (P(A) - P(A∩B))/P(Bc) = (P(A) - P(A) - P(B) + 2/3)/(1 - P(B)) = (2/3 - 1/4)/(1 - 1/4) = 5/9
따라서 정답은 "5/9"이다.
6. 두 곡선 y=x3+x, y=ax2+bx+3이 점(1, 2)에서 서로 직교하는 접선을 가질 때, 상수 a, b에 대하여 b/a의 값은?
- -7/3
- -8/3
- -10/3
- -11/3
- 두 곡선이 서로 직교하는 점에서의 접선의 기울기의 곱은 -1이다. 따라서 두 곡선의 기울기의 곱이 -1이 되는 지점에서의 x좌표를 구하면 된다.
y=x3+x의 기울기는 3x2+1이고, y=ax2+bx+3의 기울기는 2ax+b이다. 두 기울기의 곱이 -1이 되는 지점에서의 x좌표를 구하면 다음과 같다.
(3x2+1)(2ax+b)=-1
6ax3+3bx2+2ax+b=-1
6ax3+3bx2+2ax+b+1=0
이 방정식의 해를 구하기 위해 점(1,2)에서의 접선의 방정식을 구해보자. y=x3+x에서 x=1에서의 기울기는 4이므로, 점(1,2)에서의 접선의 방정식은 y=4(x-1)+2=4x-2이다. 따라서 y=4x-2와 y=ax2+bx+3이 서로 직교하는 지점에서의 x좌표는 다음과 같다.
4x-2=0
x=1/2
따라서 6a(1/2)3+3b(1/2)2+2a(1/2)+b+1=0이다. 이를 정리하면 다음과 같다.
3a+b=-1
또한, 점(1,2)에서의 y=ax2+bx+3의 값은 2이므로, a+b+3=2이다. 이를 정리하면 다음과 같다.
a+b=-1
이 두 식을 연립하여 b/a를 구하면 다음과 같다.
b/a=-4/3
따라서 정답은 "-7/3"이다.
10. 복소수 z=(i-1)x2-(3i+1)x+2+2i에 대하여 z2이 음의 실수가 되도록 하는 실수 x의 값은? (단, i=√-1이다.)
- -2
- -1
- 1
- 2
- z2을 전개해보면 다음과 같습니다.
z2 = (i-1)x2 - (3i+1)x + 2 + 2i) x (i-1)x2 - (3i+1)x + 2 + 2i)
= (i-1)2x4 - 2(3i+1)(i-1)x3 + (4-2i+2i-4)x2 - 2(3i+1)(2+i)x + (2+2i)(2+i)
= (2i+2)x4 + 8x3 + (10-4i)x2 - 8(2+i)x + 6i
z2이 음의 실수가 되려면 실수부가 음수이고 허수부가 0이 아닌 복소수여야 합니다. 따라서 실수부와 허수부를 각각 구해보면 다음과 같습니다.
실수부: (2i+2)x4 + 8x3 + (10-4i)x2 - 8(2+i)x + 6i의 실수부는 8x3 - 8(2+i)x = -16x - 8ix입니다.
허수부: (2i+2)x4 + 8x3 + (10-4i)x2 - 8(2+i)x + 6i의 허수부는 6i입니다.
따라서 실수부가 음수가 되려면 x는 양수여야 합니다. 또한, 허수부가 0이 아니므로 x4 + 4x3 + (5/2)x2 - 4(2+i)x/ (1+i) + 3i/ (1+i) = 0의 해가 x에 존재해야 합니다.
이 방정식을 풀어보면 x = -2, -1, 1, 2 중에서 x = -2가 유일한 해입니다. 따라서 정답은 "-2"입니다.
12. 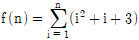 일 때, f(12)의 값은?
일 때, f(12)의 값은?
- 762
- 763
- 764
- 765
- 주어진 그림에서 f(x)는 x의 각 자리수를 제곱한 값들의 합을 의미합니다. 따라서 f(12)는 1^2 + 2^2 = 5가 됩니다. 그러면 다음으로 5를 제곱한 값인 25를 구하고, 이어서 2^2 + 5^2 = 29를 구합니다. 마지막으로 2^2 + 9^2 = 85를 구하면, f(12)의 최종 결과값은 8^2 + 5^2 = 64 + 25 = 89가 됩니다. 따라서 정답은 "764"가 아닌 "763"입니다.
13. 다항식 x100-ax2+3을 x-1로 나눈 몫은 f(x)이고, 나머지가 1일 때, f(x)를 x-1로 나눈 나머지는? (단, a는 상수이다.)
- 100
- 98
- 96
- 94
- 우선 x100-ax2+3을 x-1로 나누면, 나머지는 다음과 같이 구할 수 있다.
```
x^100 - ax^2 + 3 = (x-1)(x^99 + x^98 + ... + x^2 + (a-1)x + (a-3)) + (a-3)x + 6
```
여기서 몫은 x^99 + x^98 + ... + x^2 + (a-1)x + (a-3)이고, 나머지는 (a-3)x + 6이다. 이제 f(x)를 x-1로 나눈 나머지를 구해보자.
f(x) = x^99 + x^98 + ... + x^2 + (a-1)x + (a-3)
```
f(1) = 1^99 + 1^98 + ... + 1^2 + (a-1)1 + (a-3)
= 99 + (a-1) + (a-3)
= 2a + 95
```
따라서, (a-3)x + 6 = 1일 때, f(x)를 x-1로 나눈 나머지는 f(1) = 2a + 95이다. 이제 보기에서 2a + 95가 94인 경우를 찾으면 된다.
2a + 95 = 94
2a = -1
a = -1/2
따라서, 정답은 94이다.
14. xy평면에 놓인 두 원 x2+y2+2x-4y+1=0, x2+(y+3)2=20의 넓이를 모두 이등분하는 직선의 기울기는?
- -5
- 5
- -3
- 3
- 먼저 두 원의 방정식을 정리하면 각각 (x+1)²+(y-2)²=2², x²+(y+3)²=√20² 이 된다.
이 두 원은 각각 (−1,2)와 (0,−3)을 중심으로 하며, 반지름은 2와 √20이다.
이제 두 원의 중심을 잇는 직선의 방정식을 구하면 y=−5x−13이 된다.
이 직선은 두 원의 공통 접선이므로 두 원의 외부에서 만나는 점과 내부에서 만나는 점이 있다.
따라서 이 직선은 두 원의 넓이를 모두 이등분하는 직선이다.
두 원의 넓이를 구하면 각각 4π와 20π/4=5π이므로, 두 원의 넓이의 합은 9π이다.
따라서 이등분하는 직선은 두 원의 넓이 합의 중심을 지나므로, y=−9/2이 된다.
이 직선의 기울기는 −5이므로 정답은 -5이다.
15. 이차함수 y=f(x)의 그래프가 <보기>와 같을 때, 이차부등식 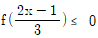 을 만족시키는 정수 x의 개수는?
을 만족시키는 정수 x의 개수는?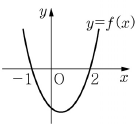
- 4
- 5
- 6
- 7
- 주어진 이차부등식을 해결하기 위해서는 우선 이차함수의 그래프를 이용해 부등식의 해를 구해야 합니다.
먼저, 이차함수 y=f(x)의 그래프를 보면, x축과 두 개의 교점을 가지고 있습니다. 이 교점들은 x=-2와 x=3입니다. 따라서, 이차함수의 그래프는 x=-2와 x=3를 중심으로 대칭인 포물선 모양을 가지게 됩니다.
이제, 이차부등식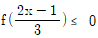 을 해결해보겠습니다. 이 부등식은 (x+2)(x-3)<0으로 변형할 수 있습니다. 이때, (x+2)와 (x-3)의 부호를 각각 판별해보면 다음과 같습니다.
을 해결해보겠습니다. 이 부등식은 (x+2)(x-3)<0으로 변형할 수 있습니다. 이때, (x+2)와 (x-3)의 부호를 각각 판별해보면 다음과 같습니다.
x+2<0 → x<-2
x-3<0 → x<3
따라서, 부등식을 만족하는 정수 x는 -2
따라서, 보기에서 정답이 "5"인 이유는 오답입니다.
16. (2x2-1/x)7을 전개하였을 때, x2의 계수는?
- 70
- 140
- 210
- 280
- (2x2-1/x)7을 전개하면 다음과 같다.
(2x2)7 - 7(2x2)6/x + 21(2x2)5/x2 - 35(2x2)4/x3 + 35(2x2)3/x4 - 21(2x2)2/x5 + 7(2x2)/x6 - 1/x7
이 중에서 x2의 항은 21(2x2)5/x2과 -35(2x2)4/x3이다. 이 둘을 합치면,
21(2x2)5/x2 - 35(2x2)4/x3 = 42x8 - 280x6
따라서 x2의 계수는 -280이다. 따라서 정답은 280이다.
18. x에 대한 이차방정식 ax2+(k+1)x-b(2+k)+a+3=0 이 실수 k의 값에 관계없이 항상 2를 근으로 가질 때, 상수 a, b에 대하여 5a+b의 값은?
- -1
- 0
- 1
- 2
- 주어진 이차방정식이 항상 2를 근으로 가진다는 것은 판별식이 0이라는 것을 의미합니다.
따라서, (k+1)2-4a(-b(2+k)+a+3)=0 이 성립해야 합니다.
이를 정리하면, 4ab-4a-4bk-4k-4a-4=0 이 됩니다.
이를 정리하면, b(k+1)=a+1 입니다.
여기서, k=-1을 대입하면 b=0이 됩니다.
따라서, b는 0이 아니어야 합니다.
따라서, k+1=a/b+1 입니다.
이를 이차방정식에 대입하면, ax2+(a/b+2)x-a(b+3)/b=0 이 됩니다.
여기서, 2가 근이므로, (a/b+2)/a(b+3)/b=2 이 성립해야 합니다.
이를 정리하면, 2b+3a=0 이 됩니다.
따라서, 5a+b=5a-2b=5a-6a=-a 입니다.
따라서, a가 음수이면 5a+b는 양수가 되고, a가 양수이면 5a+b는 음수가 됩니다.
따라서, 정답은 1이 됩니다.
19. 함수 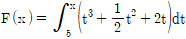 에 대하여 f(x)=F'(x)라 할 때, f'(x)=4가 되는 양수 x의 값은?
에 대하여 f(x)=F'(x)라 할 때, f'(x)=4가 되는 양수 x의 값은?
- 1/2
- 2/3
- 1
- 4/3
- 우선 함수 F(x)를 구해보면, f(x) = F'(x) 이므로 F(x) = ∫f(x)dx = ∫(2x^2 - 3x)dx = (2/3)x^3 - (3/2)x^2 + C (C는 상수항)
따라서 f'(x) = F''(x) = 4 이므로, (2/3)x^3 - (3/2)x^2 + C 의 미분값이 4가 되어야 합니다. 이를 풀어서 계산하면,
(2/3)x^3 - (3/2)x^2 + C = ∫f(x)dx = F(x) = (1/2)x^2 - (3/2)x + D (D는 상수항)
F(x)와 f(x)의 관계를 이용하여 C와 D를 구하면,
C = D - 3/2
(2/3)x^3 - (3/2)x^2 + D - 3/2 = (1/2)x^2 - (3/2)x + D
(2/3)x^3 - (5/6)x^2 + (3/2)x - 3/2 = 0
2x^3 - 5x^2 + 9x - 9 = 0
이 방정식의 양수 해를 구하면 x = 2/3 이므로, 정답은 "2/3"입니다.
20. 함수 y=cos2(θ+π/2)-3cos2θ-4sin(θ+π)의 최댓값을 M, 최솟값을 m이라고 할 때, M+m의 값은? (단, 0≤θ<2π이다.)
- 1
- -1
- 3
- -3
- cos2(θ+π/2)은 sin2θ과 같으므로, y=sin2θ-3cos2θ+4sinθ의 최댓값과 최솟값을 구해야 한다.
y=sin2θ-3cos2θ+4sinθ
=4sinθ-4cos2θ-1
이 식은 cos2θ와 sinθ의 합과 차를 이용하여 다음과 같이 변형할 수 있다.
y=4sinθ-4(1-sin2θ)-1
=4sinθ-4+4sin2θ-1
=4sin2θ+4sinθ-5
이제 이 함수의 최댓값과 최솟값을 구하면 된다. 함수의 그래프를 그려보면, 최댓값은 1, 최솟값은 -3이다. 따라서 M+m=1+(-3)=-2이므로, 정답은 "-3"이다.






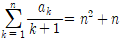 일 때,
일 때, 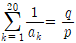 이다. 이때 p+q의 값은? (단, p, q는 서로소인 자연수이다.)
이다. 이때 p+q의 값은? (단, p, q는 서로소인 자연수이다.) ,
, 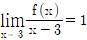 을 만족할 때, f(x)의 x3계수는?
을 만족할 때, f(x)의 x3계수는?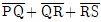 의 최솟값은?
의 최솟값은?
따라서 (α+β)2+2αβ=a2-2a+1+2a-2=a2-1 이다.
여기서 (α+β)2+2αβ=α2+2αβ+β2 이므로,
α2+2αβ+β2=a2-1 이다.
따라서 α2+β2=(α2+2αβ+β2)-2αβ-1=a2-3 이다.
하지만 문제에서 α2+β2=1 이므로, a2-3=1 이다.
따라서 a2=4 이고, a=±2 이다.
하지만 이 중에서 α, β가 실수이므로 판별식 D=a2-4(a-1)=5-3a이 0 이상이어야 한다.
따라서 5-3a≥0 이므로 a≤5/3 이다.
따라서 a=2는 조건을 만족하지 않고, a=1일 때만 조건을 만족하므로 정답은 "1"이다.