1과목: 과목 구분 없음
1.  이고
이고 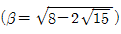 일 때 α3+β3의 값은?
일 때 α3+β3의 값은?
- 14√5
- 14√3
- 28√5
- 28√3
2. 방정식  을 만족하는 모든 실수 x의 합은?
을 만족하는 모든 실수 x의 합은?
- 5
- 6
- 4-√2
- 2-√2
3. 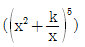 의 전개식에서 1/x2의 계수가 80 일 때, 자연수 k의 값은?
의 전개식에서 1/x2의 계수가 80 일 때, 자연수 k의 값은?
- 1
- 2
- 3
- 4
4. f(x)=3x2+1 일 때 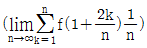 의 값은?
의 값은?
- 14
- 28
- 29
- 58
5. 복소수 z=1+√5i 일 때, z4-2z3+8z2-4z+20 의 값은?
- 2
- 4
- 6
- 8
6. N을 자연수의 집합, A={a∈N l a2-36≤0}, 그리고 B={a∈N l 세 직선 y=x, y=0, x=a 로 둘러싸인 영역의 면적이 10보다 작거나 같다}라고 하자. 집합 A∩Bc의 원소의 개수는?
- 2
- 3
- 4
- 5
7. 이차함수 f(x)=x2-4x+8의 그래프 위의 점(a, f(a))에서 접선의 방정식이 y축과 만나는 점을 P(a) 라 하자. 1≤a≤5일 때, P(a) 의 자취의 길이는?
- 24
- 27
- 30
- 33
8. f(x)=x10+1일 때  의 값은?
의 값은?
- 9/2
- 5
- 11/2
- 6
9. 함수  에 대하여, 함수 f(x)가 x=1에서 극한값을 가지기 위한 실수 a의 값은?
에 대하여, 함수 f(x)가 x=1에서 극한값을 가지기 위한 실수 a의 값은?
- 2
- 4
- 6
- 8
10. <보기>의 조건을 만족시키는 집합 A, B의 순서쌍 (A, B)의 개수는?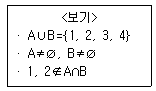
- 32
- 34
- 36
- 38
11. 수열 {an}이 a1=1과 an+1=2an+1, n=1, 2, 3, ⋯을 만족할 때,  의 값은?
의 값은?
- 2100-100
- 2100-101
- 2101-101
- 2101-102
12. 수열 {an}이 a1=2이고, 임의의 자연수 n에 대하여 a1a2···an=2n2을 만족시킨다. 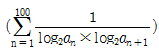 의 값이 q/p 일 때, p+q의 값은? (단, p와 q는 서로소인 자연수이다.)
의 값이 q/p 일 때, p+q의 값은? (단, p와 q는 서로소인 자연수이다.)
- 290
- 301
- 311
- 321
13. 이차방정식 x2-2kx+k+2=0 의 근 중 적어도 하나가 절댓값이 1이하가 되도록 하는 100 이하 자연수 k의 개수는?
- 83
- 88
- 93
- 98
14. 모든 실수에서 미분 가능한 함수 f(x)에 대하여 f'(x)=x+lx-1 를 만족시킨다. f(0)=3 일 때, f(-1)+f(2)의 값은?
- 6
- 8
- 10
- 12
15. 한 점에서 만나는 두 직선 l1 : x=2+t, y=1+t, z=2-t 와 l2 : x=3+t, y=2+2t, z=1+2t 사이의 각을 θ라 할 때 cosθ는? (단, 0°<θ<90°)
- 1/3√3
- 1/√3
- 1/3
- √3
16. 좌표평면 위의 원점을 지나는 직선이 곡선 y=x4+x2+2에 접할 때, 접점의 y좌표는?
- 28/9
- 32/9
- 4
- 40/9
17. 실수 x에 대해 103log(2+sinx)+cos2x의 최댓값은? (단, log는 상용로그이다.)
- 27
- 28
- 29
- 30
18. f(0)=0을 만족시키는 이차함수 f(x)에 대하여 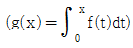 로 정의한다. 함수 g(x)가 x=2에서 최솟값을 가지고 g(6)=108 을 만족시킬 때, f(4)의 값은?
로 정의한다. 함수 g(x)가 x=2에서 최솟값을 가지고 g(6)=108 을 만족시킬 때, f(4)의 값은?
- 12
- 16
- 20
- 24
19. 확률변수 X는 0, 1또는 2의 값을 가진다. 확률변수 2X+3의 평균이 6이고 분산이 2일 때, X=2 일 확률은 q/p 이다. p+q의 값은? (단, p와 q는 서로소인 자연수이다.)
- 11
- 13
- 15
- 17
20. ΔABC에서  이다. ∠A의 이등분선이
이다. ∠A의 이등분선이 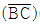 와 만나는 점을 D라 할 때,
와 만나는 점을 D라 할 때, 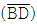 길이의 제곱은?
길이의 제곱은?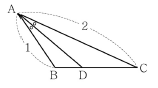






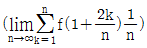 의 값은 f(4)-f(2)=49-13=36 이다. 이 값은 보기에서 유일하게 "14" 가 아닌 값이므로, 정답은 "14" 이다.
의 값은 f(4)-f(2)=49-13=36 이다. 이 값은 보기에서 유일하게 "14" 가 아닌 값이므로, 정답은 "14" 이다.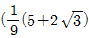
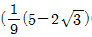
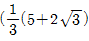
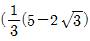
1/x2의 계수 = (a1b2c3 - a1b3c2 - a2b1c3 + a2b3c1 + a3b1c2 - a3b2c1) / (abc)2
여기서 a, b, c는 각각 1, x, x2의 계수이고, a1, a2, a3, b1, b2, b3, c1, c2, c3은 각각 전개식에서 1, x, x2의 지수입니다.
따라서 1/x2의 계수가 80이 되기 위해서는 다음과 같은 식이 성립해야 합니다.
(a1b2c3 - a1b3c2 - a2b1c3 + a2b3c1 + a3b1c2 - a3b2c1) / (abc)2 = 80
이를 간단하게 풀어쓰면 다음과 같습니다.
(a1b2c3 - a1b3c2 - a2b1c3 + a2b3c1 + a3b1c2 - a3b2c1) = 80abc2
이 식을 만족하는 자연수 k의 값은 2입니다. 이는 a1=1, a2=1, a3=1, b1=1, b2=k, b3=k2, c1=1, c2=k2, c3=k로 설정하면 확인할 수 있습니다.