1과목: 과목 구분 없음
1. <보기>와 같은 경간 L인 단순보에 등분포하중(자중 포함) w=P/3L이 작용하며, PS강재는 편심 거리 e로 직선배치 되어 프리스트레스 힘 P가 작용하고 있다. 이 보의 중앙부하단에서 휨에 의한 수직응력이 0(zero)이 되려면 편심거리 e의 크기는? (단, 경간 L은 단면 높이 h의 8배이다.)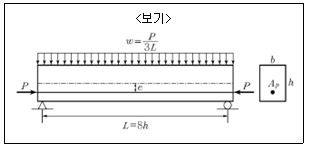
- h/6
- h/4
- h/3
- h/2
2. <보기>와 같은 기둥 단면에서 띠철근의 최대 수직간격은? (단, 정적조건을 기준으로 하며, D13의 공칭직경은 12.7mm, D35의 공칭직경은 34.9mm이다.)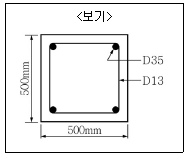
- 500mm
- 555mm
- 609mm
- 750mm
3. 기초설계와 관련한 내용으로 가장 옳은 것은? (단, Ag는 지지되는 부재의 기둥단면의 총 면적, d는 유효깊이이다.)
- 기초판 상단에서부터 철근까지의 깊이를 직접기초는 100mm 이상, 말뚝기초는 200mm 이상으로 한다.
- 다우얼철근(dowel)의 최소 면적은 0.05Ag이고, 2개 이상이어야 한다.
- 2방향 기초에서 전단에 대한 위험단면의 위치는 기둥 전면으로부터 d만큼 떨어진 곳이다.
- 전면기초 저면과 기초지반 사이에는 압축력만 작용하는 것으로 가정한다.
4. <보기>와 같이 H형 단면 압축재의 중간 위치에 약축(y축)에 대한 지지대가 설치되어 있을 때, 압축부재의 설계강도를 계산하기 위해 사용되는 세장비 kl/r은? (단, 부재 내 강축(x축) 방향으로 중간지지(intermediate bracing)는 없고, H형 단면에 대하여 rx=120mm, ry=50mm이다.)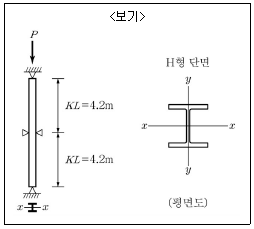
- 140
- 70
- 168
- 84
5. <보기>와 같이 철근콘크리트 기둥(단주)의 중심에 집중하중 P가 작용한다. 하중과 응력의 평형을 고려할 때 탄성과 비탄성영역의 전체 범위에 대해 타당하게 사용할 수 있는 식으로 알맞은 것은? (단, fs′=철근응력, fc=콘크리트 응력, n=Es/Ec, Ac=콘크리트 면적, As′=압축철근 면적, Ag=Ac+Ac'이다.)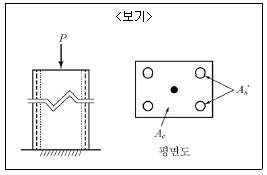
- P=fc(Ac+nAs')
- P=fc{Ag+(n-1)As'}
- P=fcAc+fc'As'
- P=fs'(Ac/n+As')
6. <보기>와 같은 옹벽에 작용하는 주동토압의 크기는? (단, 벽면마찰각과 옹벽 연직변위는 무시한다.)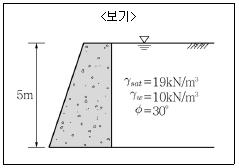
- 32.5kN/m
- 162.5kN/m
- 287.5kN/m
- 325kN/m
7. 옹벽 설계와 관련한 내용 중 가장 옳지 않은 것은?
- 부벽식 옹벽의 뒷부벽은 T형보로 설계한다.
- 캔틸레버식 옹벽의 전면벽은 저판에 지지된 캔틸레버로 설계할 수 있다.
- 활동에 대한 저항력은 옹벽에 작용하는 수평력의 1.5배 이상, 전도에 대한 저항휨모멘트는 횡토압에 의한 전도모멘트의 2.0배 이상이어야 한다.
- 부벽식 옹벽의 전면벽은 2변 지지된 1방향 슬래브로 설계할 수 있다.
8. 슬래브 설계기준에 관한 설명으로 가장 옳지 않은 것은?
- 2방향 슬래브의 위험단면에서 주철근의 간격은 슬래브 두께의 2배 이하이어야 하고, 또한 300mm 이하이어야 한다.
- 슬래브에서 주철근이 1방향으로만 배치되는 경우에는 주철근에 평행하게 건조수축철근과 온도철근을 배치해야 한다.
- 1방향 슬래브는 최대 휨모멘트가 일어나는 단면에서 정철근과 부철근의 중심 간격이 슬래브 두께의 2배 이하이어야 하고, 또한 300mm 이하이어야 한다.
- 슬래브가 네 변에서 지지되고 짧은 변에 대한 긴 변의 비가 2보다 작을 때 2방향 슬래브라고 한다.
9. 이형철근의 정착과 관련한 내용 중 가장 옳지 않은 것은? (단, lab는 기본정착길이, ld는 정착길이, db는 철근지름, fy는 철근의 설계기준항복강도이다.)
- 인장 이형철근의 정착길이는 기본정착길이에 보정계수를 곱하여 구하며, 이때 정착길이는 300mm 이상이어야 한다.
- 압축 이형철근의 기본 정착길이는 0.043dbfy 이상이어야 한다.
- 표준갈고리를 갖는 인장 이형철근의 정착길이는 150mm이상이어야 하며, 갈고리는 압축을 받는 경우 철근정착에 유효한 것으로 보아야 한다.
- 철근의 설계기준항복강도가 400MPa 이하인 경우 확대 머리 이형철근의 정착길이는 150mm 이상이어야 한다.
10. 콘크리트에서 발생하는 크리프(creep)와 관련한 설명으로 가장 옳지 않은 것은?
- 물시멘트비와 시멘트량이 감소할수록 크리프는 감소한다.
- 수화율이 증가할수록 크리프는 감소한다.
- 상대습도가 클수록 크리프는 증가한다.
- 고온 증기양생한 콘크리트는 크리프가 감소한다.
11. 프리스트레스트콘크리트 구조물의 프리스트레스 손실 중 포스트텐션방식에서만 고려하는 것은?
- 콘크리트의 탄성수축에 의한 손실
- 콘크리트의 크리프에 의한 손실
- 긴장재와 덕트 사이의 마찰에 의한 손실
- 긴장재의 릴랙세이션에 의한 손실
12. <보기>와 같은 다음 복철근보가 휨극한 상태에 도달했을 때 인장철근의 변형률이 최소허용변형률이었다면 압축철근에 발생하는 응력은? (단, 콘크리트구조설계기준(2012)을 적용하며, fy=500MPa이다.)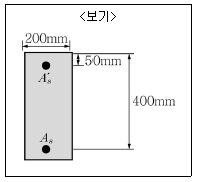
- 300MPa
- 400MPa
- 450MPa
- 500MPa
13. 브래킷, 내민받침 등에 적용하는 전단마찰철근의 설계기준 항복강도의 최댓값은? (단, 콘크리트 조기준(2012)을 적용한다.)
- 400MPa
- 500MPa
- 550MPa
- 600MPa
14. <보기>와 같이 콘크리트 구조기준(2012)에서 규정된 비틀림설계에 대한 설명 중 옳은 내용을 모두 고른 것은?
- ㉠, ㉤
- ㉠, ㉣
- ㉡, ㉢
- ㉣, ㉤
15. 압축이형철근의 겹침이음 길이에 대한 설명으로 가장 옳은 것은?
- 서로 다른 크기의 철근을 압축부에서 겹침이음하는 경우, 이음길이는 크기가 큰 철근의 겹침이음길이와 크기가 작은 철근의 정착길이 중 큰 값 이상이어야 한다.
- fy>400MPa이면 0.072dbfy이하, fy≤400MPa이면 (0.13fy-24)db이하이다.
- fck<24MPa일 때 규정된 겹침이음길이를 1/3만큼 증가시켜야 한다.
- 나선철근 압축부재의 나선철근으로 둘러싸인 축 방향 철근의 겹침이음길이에 계수 0.75를 곱할 수 있으나 겹침 이음길이는 300mm 이상이어야 한다.
16. <보기>와 같은 보의 단면에 10kN의 전단력이 작용하는 경우 단면의 중립축(N · A)에서 10cm 떨어진 A점에서의 전단응력 값은?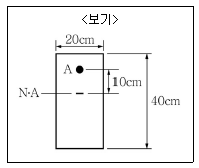
- 9.4N/cm2
- 14N/cm2
- 0.2N/cm2
- 0.02N/cm2
17. <보기>의 그림 (가)와 같이 중앙 지점에 집중하중이 작용하는 단순보가 그림 (나)와 같이 (6×20)cm의 단면으로 이루어진 경우 최대 휨응력은?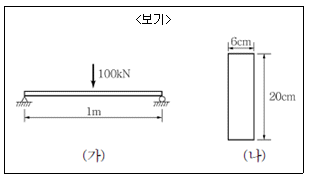
- 6.25kN/cm2
- 12.65kN/cm2
- 166.75kN/cm2
- 833kN/cm2
18. 길이 100m의 양단이 고정된 레일은 단면적 A=50cm2, 열팽창계수 α=1.5×10-6/℃, 탄성계수 E=200GPa이다. 이 경우 온도가 10℃ 상승할 때 레일에 발생되는 열응력의 값은? (단, 마찰은 무시한다.)
- 3,000kN/m2
- 600kN/m2
- 3kN/m2
- 60kN/m2
19. <보기>와 같이 볼트의 직경이 4cm이며 mp의 길이가 5cm이고 인장하중 P=20kN을 받는 볼트의 연결부에서 볼트 mnpq 부분의 지압응력 값은?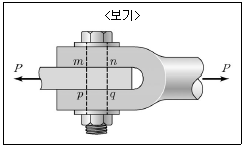
- 1.6kN/cm2
- 2.35kN/cm2
- 1.25kN/cm2
- 1kN/cm2
20. <보기>와 같은 응력도를 갖는 단철근 직사각형보에서 콘크리트 응력도의 응력 최대치는 0.85fck, fck=20MPa, fy= 400MPa일 때 공칭 휨강도는?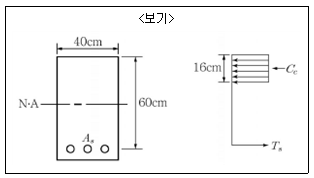
- 665kN · m
- 1.7kN · m
- 565kN · m
- 33kN · m






우선, 보의 단면은 직사각형이므로 단면 2차 모멘트를 구해야 합니다. 단면 2차 모멘트는 다음과 같습니다.
$I = frac{1}{12}bh^3$
여기서, 경간 L은 단면 높이 h의 8배이므로 L = 8h입니다. 따라서, 단면 2차 모멘트는 다음과 같이 나타낼 수 있습니다.
$I = frac{1}{12}(8h)h^3 = frac{4}{3}h^4$
이제, 편심거리 e를 구하기 위해 균형방정식을 세워야 합니다. 균형방정식은 다음과 같습니다.
$P = frac{wL}{2} + Pe$
여기서, $frac{wL}{2}$는 중심하중입니다. 중심하중은 보의 중심에서 작용하는 하중으로, 이 경우에는 보의 중앙부하단에서 작용하는 하중입니다. 따라서, 중심하중은 다음과 같이 나타낼 수 있습니다.
$frac{wL}{2} = frac{P}{3}$
균형방정식을 편심거리 e에 대해 정리하면 다음과 같습니다.
$Pe = frac{2P}{3}$
이제, 휨에 의한 수직응력이 0이 되는 조건을 이용하여 편심거리 e를 구할 수 있습니다. 휨에 의한 수직응력이 0이 되는 조건은 다음과 같습니다.
$frac{M}{I}y = frac{P}{2}$
여기서, M은 휨모멘트, y는 수직응력이 0이 되는 위치입니다. 이 경우에는 보의 중앙부하단에서 수직응력이 0이 되어야 하므로 y는 $frac{h}{2}$입니다. 따라서, 휨모멘트 M은 다음과 같이 나타낼 수 있습니다.
$M = frac{wL^2}{8} - Pe$
이를 균형방정식에 대입하면 다음과 같습니다.
$frac{frac{wL^2}{8} - Pe}{I}frac{h}{2} = frac{P}{2}$
여기서, I는 위에서 구한 단면 2차 모멘트입니다. 이를 정리하면 다음과 같습니다.
$e = frac{h}{6}$
따라서, 정답은 "h/6"입니다.