1과목: 과목 구분 없음
1. 단철근 직사각형 단면의 공칭휨강도(Mn)가 360kN⋅m인 경우 단면의 유효깊이(d)는 약 얼마인가? (단, fck=24MPa, fy=350MPa, bw=280mm, As=2,160mm2)
- 383.4mm
- 436.4mm
- 490.4mm
- 542.4mm
2. 휨설계 일반 원칙에 대한 설명으로 가장 옳지 않은 것은?
- 균형 변형률 상태는 인장 철근이 설계기준 항복 강도 fy에 대응하는 변형률에 도달하고 동시에 압축 콘크리트가 가정된 극한 변형률 0.003에 도달할 때이다.
- 압축 지배 변형률 한계는 균형 변형률 상태에서 인장 철근의 순인장 변형률과 같다.
- 휨부재의 최소 허용 변형률은 fy≤400MPa인 경우에 0.004이고, fy>400MPa인 경우에는 철근 항복 변형률의 2배이다.
- 철근의 항복 강도가 400MPa을 초과하는 경우에는 인장 지배 변형률 한계를 철근 항복 변형률의 2배로 한다.
3. <보기>와 같은 균형 단면의 직사각형보에서 설계기준강도 fck가 33MPa이라면 계수 β1은? (단, c는 압축측 연단에서 중립축까지 거리이다.)(2022년 개정된 규정 적용됨)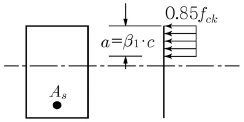
- 0.85
- 0.80
- 0.74
- 0.65
4. <보기>와 같이 단철근 직사각형 철근콘크리트 보의 휨균열을 일으키는 휨모멘트(Mcr)는 약 얼마인가? (단, 콘크리트의 파괴계수(fr)는 3.0MPa이다.)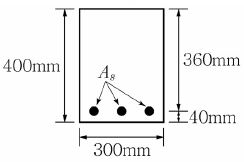
- 20kN⋅m
- 22kN⋅m
- 24kN⋅m
- 26kN⋅m
5. 장변이 6m이고, 단변이 4m인 독립확대기초에서 단변 방향으로 배치할 총 철근량이 3,000mm2이다. 이때 단변 방향으로 단변의 폭만큼 중앙 구간에 등간격으로 배치할 철근량은?
- 2,400mm2
- 3,000mm2
- 1,500mm2
- 1,200mm2
6. PSC 보에서 정착장치에 의한 응력손실과 관련하여 덕트와 PS강재 사이의 부착유무에 따른 설명으로 가장 옳지 않은 것은? (단, lset은 마찰력과 미끌림에 의한 응력손실이 평형을 이루는 길이를 의미한다.)
- 비부착긴장재의 경우 PS강재는 부재 전체 길이에서 일정한 크기로 변형된다.
- 부착긴장재의 경우 응력손실은 부재 단부에서 최대가 되지만, 안쪽으로 들어갈수록 작아진다.
- 부착긴장재의 경우 PS강재의 응력은 부재 단부에서 부재 안쪽으로 들어갈수록 증가한다.
- 부착 및 비부착긴장재에 따른 응력은 부재 단부로부터 거리 lset가 되었을 때 동일하게 된다.
7. <보기>와 같은 리벳이음에서 판이 지압에 의해 파괴되기 위한 판 두께 t는 얼마 이하인가? (단, 직경 ø=20mm, 허용전단응력 va=120MPa, 허용 지압응력 fba=300MPa이다.)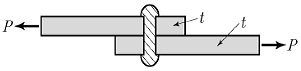
- 6.28mm
- 7.53mm
- 8.36mm
- 9.83mm
8. <보기>와 같이 단순지지된 2방향 슬래브에 등분포하중 w가 작용할 때 긴 변이 부담하는 하중 wL과 짧은 변이 부담하는 하중 ws에 대한 식으로 가장 옳은 것은? (단, L은 2방향 슬래브의 긴 변 길이, S는 2방향 슬래브의 짧은 변 길이를 나타낸다.)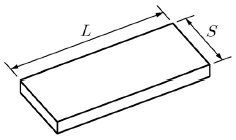
9. <보기>의 단면을 가진 철근콘크리트 보가 정모멘트 작용 시 휨 극한상태에서 순인장변형률 εt=0.006이 발생한다고 할 때 콘크리트 압축력 계산을 위한 등가직사각형 응력 깊이 a는? (단, fck=24MPa이다.)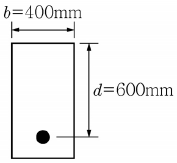
- 150mm
- 170mm
- 200mm
- 235mm
10. 콘크리트의 크리프계수 보정과 직접적으로 관련이 없는 요소로 가장 옳은 것은?
- 양생온도 및 시멘트 종류
- 작용 응력의 크기
- 온도 변화
- 콘크리트 휨강도
11. 철근 배치 원칙으로 가장 옳지 않은 것은?
- 철근은 콘크리트를 치기 전에 정확하게 배치되고 움직이지 않도록 적절하게 지지되어야 하며, 시공이 편리하도록 배치되어야 한다.
- 철근은 「콘크리트 구조기준(2012)」에 명시된 허용오차 이내에서 규정된 위치에 배치되어야 한다. 다만, 책임구조기술자가 승인한 경우에는 허용오차를 벗어날 수 있다.
- 경간이 5.0m 이하인 슬래브에 사용되는 지름이 6.4mm 이하인 용접철망이 받침부를 지나 연속되어 있거나 받침부에 확실하게 정착되어 있는 경우, 이 용접철망은 받침부 위의 슬래브 상단부근의 한 점부터 경간 중앙의 슬래브 바닥 부분의 한 점까지 구부릴 수 있다.
- 철근 조립을 위해 교차되는 철근은 용접할 수 없다. 다만, 책임구조기술자가 승인한 경우에는 용접할 수 있다.
12. <보기>와 같이 T형 단면보에서 전단철근이 부담하는 공칭전단력(Vs)는 약 얼마인가? (단, 보통중량 콘크리트를 사용하며 콘크리트의 설계기준압축강도(fck)는 25MPa, 전단철근의 설계기준항복강도(fyt)는 400MPa이고, 철근 D10을 수직 스터럽(stirrup)으로 사용하며, 스터럽의 간격은 180mm, D10 철근 1본의 단면적은 71mm2이다.)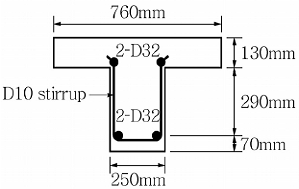
- 132.5kN
- 137.5kN
- 142.5kN
- 147.5kN
13. <보기>와 같이 길이 20m인 보에 PS 긴장재를 포물선 배치하여 P=4,000kN으로 긴장할 때 등분포 상향력 u는 얼마인가? (단, 폭 b=400mm, 새그 s=250mm이다.)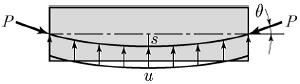
- 20kN/m
- 25kN/m
- 30kN/m
- 40kN/m
14. 철근콘크리트 슬래브에 대한 설명으로 가장 옳지 않은 것은?
- 4변에 의해 지지되는 2방향 슬래브 중에서 단변에 대한 장변의 비가 2배를 넘으면 1방향 슬래브로 해석한다.
- 슬래브 끝의 단순받침부에서도 내민슬래브에 의하여 부모멘트가 일어나는 경우에는 이에 상응하는 철근을 배치하여야 한다.
- 슬래브의 단변방향 보의 상부에 부모멘트로 인해 발생하는 균열을 방지하기 위하여 슬래브의 단변방향으로 슬래브 상부에 철근을 배치하여야 한다.
- 1방향 슬래브에서는 정모멘트 철근 및 부모멘트 철근에 직각방향으로 수축⋅온도철근을 배치하여야 한다.
15. <보기>와 같은 중력식 옹벽의 무게 W=90kN이고 옹벽에 작용하는 수평력 H=20kN일 때 전도에 대한 안전율과 활동에 대한 안전율은? (단, 옹벽의 무게 및 수평력은 단위폭 당 값이며 옹벽의 저판 콘크리트와 흙 사이의 마찰계수는 0.4이다.)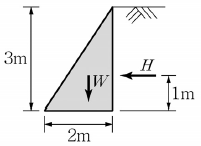
- 전도에 대한 안전율: 3.0, 활동에 대한 안전율: 1.5
- 전도에 대한 안전율: 3.0, 활동에 대한 안전율: 1.8
- 전도에 대한 안전율: 6.0, 활동에 대한 안전율: 1.5
- 전도에 대한 안전율: 6.0, 활동에 대한 안전율: 1.8
16. <보기>와 같이 직사각형 단면보가 3개의 D29 인장철근으로 보강되어 있을 때 단면 중립축의 깊이는 압축연단으로부터 약 얼마인가? (단, 콘크리트의 설계기준압축강도(fck)는 28MPa이며 철근의 설계기준항복강도(fy)는 400MPa이다.)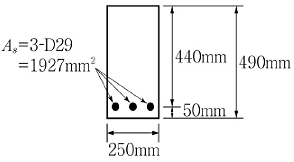
- 152.4mm
- 157.4mm
- 162.4mm
- 167.4mm
17. 「콘크리트구조기준(2012)」에서 아치의 좌굴에 대한 검토 시, 아치 리브를 설계할 때는 응력 검토뿐만 아니라 면내 및 면외방향의 좌굴에 대한 안정성을 규정에 따라 확인하도록 제시한 것과 관련한 설명으로 가장 옳지 않은 것은? (단, λ=세장비이다.)
- λ≤ 10인 경우 좌굴 검토는 필요하지 않다.
- 20<λ≤60인 경우 유한변형에 의한 영향을 편심하중에 의한 휨모멘트로 치환하여 발생하는 휨모멘트에 더하여 단면의 계수휨모멘트에 대한 안정성을 검토하여야 한다.
- 60<λ≤100의 경우 부재 재료의 비선형성을 고려하여 좌굴에 대한 안정성을 검토하여야 한다.
- λ>200의 경우 아치구조물로서 적합하지 않다.
18. PS 강재의 정착 방법 중에서 쐐기식 공법에 해당하지 않는 것은?
- VSL 공법
- CCL 공법
- Magnel 공법
- Leoba 공법
19. <보기>는 콘크리트 속에 매설된 철근이 한쪽 끝에서 인장력(T)을 받고 있음을 나타낸다. 철근의 정착길이(Id)에 대한 식으로 가장 옳은 것은? (단, As는 인장철근의 단면적, fy는 철근의 설계기준항복강도, uu는 철근과 콘크리트의 극한공칭부착강도, db는 철근의 공칭지름을 나타낸다.)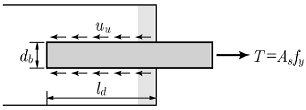
20. <보기>와 같이 지간 10m의 프리스트레스트 콘크리트 단순보에 자중을 포함한 하중이 24kN/m의 등분포하중으로 작용하고 있다. 부재 단면은 폭 500mm, 높이 800mm이고 PS강선이 편심 e=0.2m로 직선배치되어 있을 때 이 보의 중앙부 하단 응력이 0이 되도록 하는 프리스트레스트 힘 P의 크기는?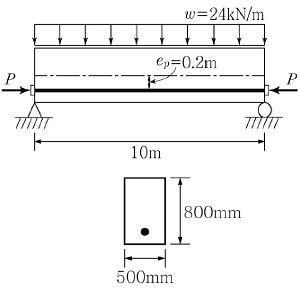
- 900kN
- 1,100kN
- 1,300kN
- 1,500kN






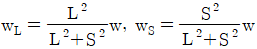
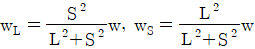
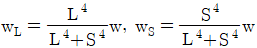
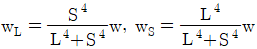
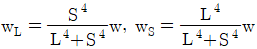 "이다.
"이다.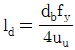
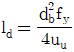
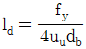
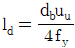
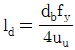 "이다.
"이다.
Mn = 0.9 × fy × As × (d - a/2)
여기서, fy는 철근의 항복강도, As는 철근 단면적, d는 단면의 유효깊이, a는 단면의 전체높이, 즉 a = bw + 2hfy입니다.
주어진 문제에서는 Mn = 360kN⋅m, fy = 350MPa, As = 2,160mm2, bw = 280mm, fck = 24MPa입니다.
먼저, a를 구해보겠습니다.
a = bw + 2hfy = 280 + 2 × 25 × 350 = 2,030mm
다음으로, Mn의 식에 주어진 값을 대입하여 d를 구합니다.
360 × 106 = 0.9 × 350 × 2,160 × (d - 2,030/2)
d - 1,015 = 1,028.57
d = 2,043.57mm
하지만, 이 값은 전체높이 a보다 크므로, 실제 유효깊이는 a보다 작아야 합니다. 따라서, d = a - x로 높이를 조정해야 합니다.
여기서 x는 단면의 상부 덮개 높이입니다. 일반적으로 x는 0.5hfy 이하로 설정합니다.
주어진 보기 중에서 x = 0.5hfy = 25 × 0.5 = 12.5mm일 때, d = a - x를 계산하면,
d = 2,030 - 12.5 = 2,017.5mm
따라서, 답은 "490.4mm"이 됩니다.
참고로, x를 다른 값으로 설정하면 다른 답이 나올 수 있습니다. 예를 들어, x = 0.3hfy = 25 × 0.3 = 7.5mm일 때, d = a - x를 계산하면,
d = 2,030 - 7.5 = 2,022.5mm
이므로, 답은 "542.4mm"이 됩니다.