1. 단면이 300×500mm의 직사각형인 철근콘크리트 부재가 있다. 철근은 단면 도심에 대칭으로 배치되었으며, 철근 단면적 As=5,000mm2이다. 콘크리트의 건조수축으로 인해 철근에 발생하는 압축응력이 60MPa일 때, 건조수축에 의해 콘크리트에 발생하는 응력은? (단, 이 부재의 지점 변형은 구속되어 있지 않다.)
- 1MPa
- 2MPa
- 3MPa
- 4MPa
2. 휨을 받는 띠철근으로 보강된 직사각형 단면에서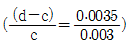 
일 때, 강도감소계수의 값은? (단, 인장 철근은 1열로 배치되어 있으며, d는 유효깊이, c는 중립축깊이, 철근 항복강도 fy=400MPa이고, 「콘크리트구조 기준(2012)」을 적용한다.)
- 0.65
- 0.70
- 0.75
- 0.85
3. 그림과 같은 정(+)의 휨모멘트가 작용하는 T형보를 설계할 때, 유효폭 be를 폭으로 하는 직사각형보로 해석 할 수 있는 유효폭 be의 최솟값은? (단, fck=20MPa, fy=400MPa이고, 「콘크리트구조기준(2012)」을 적용한다.)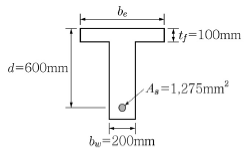
- 250mm
- 300mm
- 350mm
- 400mm
4. 철근콘크리트 압축부재의 장주설계에 대한 설명으로 가장 옳지 않은 것은? (단, 「콘크리트구조기준(2012)」을 적용한다.)
- 비횡구속 골조의 압축부재의 경우, klu/r≤22이면 장주효과를 무시할 수 있다.
- 횡구속 골조의 압축부재의 경우, klu/r≤34-12(M1/M2)이면 장주효과를 무시할 수 있다.
- 압축부재의 비지지길이 lu는 바닥슬래브, 보, 기타 고려하는 방향으로 횡지지할 수 있는 부재들 사이의 순길이로 한다.
- 기둥머리나 헌치가 있는 경우의 비지지길이는 검토 하고자 하는 면이 있는 기둥머리나 헌치의 최상단 까지 측정된 거리로 한다.
5. 큰 처짐에 의해 손상되기 쉬운 칸막이벽이나 기타 구조물을 지지하지 않는 지간 5m의 1방향 슬래브가 단순 지지되어 있다. 처짐을 계산하지 않는 경우, 슬래브의 최소 두께는? (단, 부재는 보통중량 콘크리트와 설계기준항복강도 300MPa 철근을 사용한 리브가 없는 1방향 슬래브이고, 「콘크리트구조기준(2012)」을 적용한다.)
- 200mm
- 215mm
- 250mm
- 300mm
6. RC복철근 직사각형 단면의 보에서 인장철근의 단면적은 그대로인 상태로 압축철근의 단면적만 2배로 증가시켰을 때, 단면의 응력 및 변형률 분포에 대한 설명으로 옳지 않은 것은? (단, 두 경우 모두 인장 및 압축철근은 항복한 것으로 가정한다.)
- 콘크리트의 등가 압축응력 블록 깊이가 감소한다.
- 콘크리트와 압축철근에 의한 압축 내력의 합이 증가한다.
- 휨모멘트의 팔길이가 증가한다.
- 압축철근의 변형률이 감소한다.
7. 프리텐션 부재에 프리스트레스를 도입하였을 때, 도입직후 긴장재 도심 위치에서의 콘크리트 응력(fcs)이 7MPa로 산정되었다. 크리프 계수 Cu=2.0, 탄성계수 비 n=Ep/Ec=6, 콘크리트 건조수축변형률 εsh=20×10-5, 긴장재의 탄성계수 Ep=2.0×105MPa일 때, 콘크리트의 크리프와 건조수축으로 인한 프리스트레스 손실량의 합은?
- 96MPa
- 112MPa
- 124MPa
- 138MPa
8. 2방향 슬래브 구조를 해석하기 위한 근사적 방법인 직접설계법을 적용하기 위한 제한사항으로 옳지 않은 것은? (단, 「콘크리트구조기준(2012)」을 적용한다.)
- 연속한 기둥 중심선을 기준으로 기둥의 어긋남은 그 방향 경간의 10% 이하이어야 한다.
- 모든 하중은 슬래브 판 전체에 걸쳐 등분포된 연직하중이어야 하며, 활하중은 고정하중의 2배 이하이어야 한다.
- 각 방향으로 연속한 받침부 중심간 경간 길이의 차이는 긴 경간의 1/3 이하이어야 한다.
- 슬래브 판들은 단변 경간에 대한 장변 경간의 비가 2 이상인 직사각형이어야 한다.
9. 그림과 같은 철근콘크리트 내민보에 자중을 포함한 계수등분포하중(wu)이 100kN/m로 작용할 때, 위험단면에서 전단보강철근이 부담해야 할 최소의 전단력(Vs)을 부담한다면 전단보강철근의 최대간격은 얼마 이하여야 하는가? (단, 보통중량 콘트리트를 사용하였으며, fck=36MPa, 전단철근의 단면적 Av=400mm2, fyt=300MPa이며, 「콘크리트구조기준(2012)」을 적용한다.)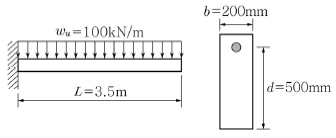
- 125mm
- 200mm
- 250mm
- 300mm
10. 그림과 같이 하중을 받은 무근콘크리트 내민보의 단면에서 휨균열이 발생하는 보의 최대 높이 h는? (단, 콘크리트는 보통중량 콘크리트, 설계기준강도 fck=36MPa, 「콘크리트구조기준(2012)」을 적용한다.)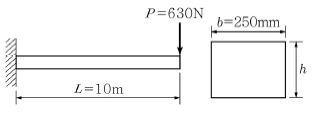
- 100mm
- 200mm
- 300mm
- 400mm
11. 인장 이형철근 및 이형철선의 정착길이 ld는 기본정착 길이 ldb에 보정계수를 고려하는 방법이 적용될 수 있다. ＜보기＞는 기본정착길이 ldb를 구하기 위한 식이다. 이 식에 적용되는 보정계수 α, β, λ에 대한 설명 중 옳지 않은 것은?
- 철근배치 위치계수인 α는 정착길이 또는 겹침이음부 아래 300mm를 초과되게 굳지 않은 콘크리트를 친 수평철근일 경우 1.3이다.
- 철근 도막계수인 β는 피복두께가 3db 미만 또는 순간격이 6db 미만인 에폭시 도막철근 또는 철선일 경우 1.5이다.
- 에폭시 도막철근이 상부철근인 경우에 상부철근의 위치계수 α와 철근 도막계수 β의 곱, αβ가 1.8보다 클 필요는 없다.
- 경량콘크리트계수인 λ는 경량콘크리트 사용에 따른 영향을 반영하기 위하여 사용하는 보정계수이며 전경량 콘크리트의 경량콘크리트계수는 0.75이다.
12. 그림과 같은 정사각형 띠철근 기둥(단주)에 편심을 갖는 공칭 축하중 Pn 이 작용하여 압축응력블록의 깊이 a가 255mm이라면 인장철근력 T의 크기는? (단, fck=20/0.85MPa, a=0.85×300mm, AsA's=1,000mm2, fy=400MPa, Es=2×105MPa이다.)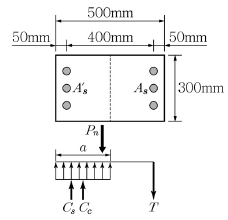
- 200kN
- 250kN
- 300kN
- 400kN
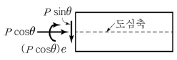
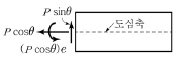
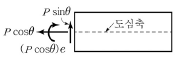
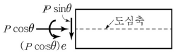
13. 그림과 같은 긴장재를 절곡 배치한 프리스트레스트 콘크리트 부재의 A-A 단면에서 프리스트레스 힘에 의해 작용하는 단면력이 옳은 것은?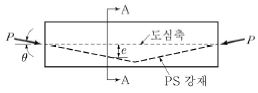
-
CBT문제은행AI2023-04-12 08:26
A-A 단면에서는 긴장재의 힘이 수직방향으로 작용하므로, 긴장재의 힘은 단면력으로 변환됩니다. 이 때, 긴장재의 힘은 상부와 하부에서 서로 상쇄되므로, 단면력은 중립면에서 가장 큽니다. 따라서, 옳은 답은 "
" 입니다.
14. 옹벽 설계에 대한 설명으로 옳지 않은 것은? (단, 「콘크리트구조기준(2012)」을 적용한다.)
- 옹벽은 외력에 대하여 활동, 전도 및 지반침하에 대한 안정성을 가져야 하며, 이들 안정은 계수하중에 의하여 검토한다.
- 활동에 대한 저항력은 옹벽에 작용하는 수평력의 1.5배 이상이어야 한다.
- 전도에 대한 저항 휨모멘트는 횡토압에 의한 전도 모멘트의 2.0배 이상이어야 한다.
- 지반 침하에 대한 안정성 검토 시에 최대지반반력은 지반의 허용지지력 이하가 되도록 한다. 지반의 내부 마찰각, 점착력 등과 같은 특성으로부터 지반의 극한 지지력을 구할 수 있다. 다만, 이 경우에 허용지지력 qa는 qu/3이어야 한다.
15. 그림과 같은 철근콘크리트 확대기초에서 긴변 방향의 위험단면에서 휨모멘트는? (단, 하중은 계수하중이다.)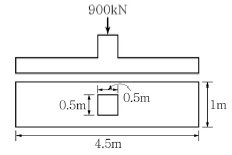
- 28kN· m
- 100kN· m
- 400kN· m
- 800kN· m
16. 철근콘크리트 부재나 프리스트레스트 부재의 경우 ＜보기＞의 식에 따라 최소 전단철근량을 산정하여야 한다. 최소 전단철근에 관한 설명 중 옳지 않은 것은?
- 계수전단력 Vu가 콘크리트에 의한 공칭전단강도 Vc의 1/2을 초과하는 모든 철근콘크리트 및 프리스트레스트콘크리트 휨부재에 최소 전단철근을 배치하여야 한다.
- 전체 깊이가 250mm 이하이거나 I형보, T형보에서 그 깊이가 플랜지 두께의 2.5배 또는 복부폭의 1/2 중 큰 값 이하인 보는 최소 전단철근을 배치하지 않아도 된다.
- 교대 벽체 및 날개벽, 옹벽의 벽체, 암거 등과 같이 휨이 주거동인 판부재는 최소 전단철근을 배치하지 않아도 된다.
- 최소 전단철근량은 0.35bws/fyt보다 작지 않아야 한다. 여기서, bw와 s의 단위는 mm이다.
17. 프리스트레스트콘크리트 설계에 관한 설명으로 옳지 않은 것은? (단, 「콘크리트구조기준(2012)」을 적용한다.)
- 프리스트레스를 도입할 때, 사용하중이 작용할 때, 그리고 균열하중이 작용할 때의 응력계산은 선형탄성 이론을 따른다.
- 프리스트레스트콘크리트 휨부재는 미리 압축을 가한 인장구역에서 사용하중에 의한 인장연단응력 ft에 따라 비균열등급, 부분균열등급, 완전균열등급으로 구분된다.
- 2방향 프리스트레스트콘크리트 슬래브는 ft≤0.63√fck를 만족하는 비균열등급 부재로 설계되어야 한다. (단, fck=콘크리트의 설계기준압축강도)
- 휨부재의 설계휨강도 계산은 강도설계법에 따라야 하며, 이때 긴장재의 응력은 fy 대신 fps를 사용한다. (단, fy=철근의 설계기준항복강도, fps=긴장재의 인장응력)
18. 단철근 직사각형보의 압축연단 콘크리트가 가정된 극한변형률인 0.003에 도달할 때 최외단 인장철근의 순인장변형률 εt가 인장지배한계변형률 한계 이상인 단면을 유지할 수 있는 최대철근비 pt는 균형철근비 pb의 몇 배인가? (단, fy=600MPa, fck=25MPa, 「콘크리트구조기준(2012)」을 적용한다.)
- 3/4
- 4/7
- 5/9
- 5/7
19. 그림과 같은 보에서 4개의 종방향 인장철근 중 2개를 절단할 수 있는 이론적인 절단점의 길이 x는? (단, 인장 철근이 2개인 단면의 설계휨모멘트 øMn=100kN· m)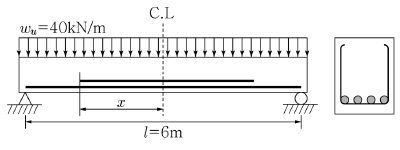
- 1,000mm
- 1,200mm
- 1,600mm
- 2,000mm
20. 「도로교 설계기준(2015)」에 제시된 콘크리트 교량구조의 한계상태에 대한 설명으로 가장 옳지 않은 것은?
- 사용한계상태는 사용자의 안전을 위험하게 하는 구조적 손상 또는 파괴에 관련된 것이다.
- 극한한계상태를 부재의 정역학적 평형 손실 한계상태 등에 대하여 검토한다.
- 한계상태는 설계에서 요구하는 성능을 더 이상 발휘할 수 없는 한계이다.
- 피로한계상태는 교량의 사용 수명 동안 작용하는 활하중에 의한 교번응력에 대하여 검토한다.