1과목: 과목 구분 없음
1. 0[dBm]의 전력을 갖는 신호가 손실이 30[dB]인 시스템을 통과하는 경우, 출력신호의 크기는?
- 0[mW]
- 0.1[mW]
- 0.01[mW]
- 0.001[mW]
2. 신호 x(t)=cosw0t+sin22w0t의 복소 지수 푸리에 급수(Fourier series)로 가장 옳지 않은 것은? (단, 여기서 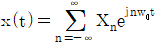 이다.)
이다.)
- X1=1/2
- X2=0
- X3=0
- X4=1/4
3. s1=(101011)과 s2=(001101) 간의 해밍 거리는?
- 2
- 3
- 4
- 5
4. 어느 해 서울특별시 9급 통신이론 시험의 점수를 평균 ax=80점과 표준편차 σx=10점을 가진 Gauss 랜덤변수 X라 가정할 때, 시험 점수가 90점보다 더 높을 확률로 가장 옳은 것은? (다음 표는 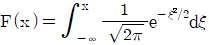 에서 x의 변화에 대한 F(x) 값이다.)
에서 x의 변화에 대한 F(x) 값이다.)
- 약 30.8%
- 약 15.9%
- 약 6.7%
- 약 2.3%
5. <보기>와 같이 폭이 τ이고 높이가 A인 구형함수로 이루어진 파형의 푸리에 변환(Fourier Transform)으로 가장 옳은 것은? (단, 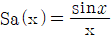 이고
이고 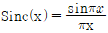 이다.)
이다.)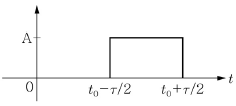
6. 순회 잔여 검사 부호(Cyclic Redundancy Check(CRC) Code)에서 메시지 D=1010001101이고 나눗수 P=110101 일 때 전송되는 부호 T로 가장 옳은 것은?
- 101000110101110
- 101000110111001
- 101000110101101
- 101000110110110
7. 메시지 신호 m(t)=Acosωmt를 주파수 변조하였을 때 변조된 반송파의 위상 편이로 가장 옳은 것은? (단, kf는 주파수-편이 상수이다.)
- Akfcosωmt
- Akfsinωmt
- (Akf/ωm)cosωmt
- (Akf/ωm)sinωmt
8. 변조신호 x(t)=10cos200πt를 임펄스 열 p(t)= 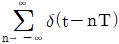 를 이용하여 DSB-SC 변조하려고 한다. 이때 x(t)p(t)에 나타나는 주파수 성분으로 가장 옳은 것은? (단, T=1/1,000[s]이다.)
를 이용하여 DSB-SC 변조하려고 한다. 이때 x(t)p(t)에 나타나는 주파수 성분으로 가장 옳은 것은? (단, T=1/1,000[s]이다.)
- 1000n±100[Hz]
- 1000n±200[Hz]
- 2000n±100[Hz]
- 2000n±200[Hz]
9. 1Mbits/s의 비트율을 갖는 BPSK 시스템에 대한 비트 오류 확률 PB로 가장 옳은 것은? (단, 수신된 파형들인 s1=Acosω0t와 s2=-Acosω0t는 정합 필터로 동기적으로 검출된다. 진폭 A=10mV이고 단측 잡음 전력 스펙트럼 밀도 N0=10-11W/Hz이다. 신호 전력과 비트당 에너지는 1Ω부하에 대해 정규화되었다. 그리고 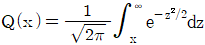 이다.)
이다.)
- PB=Q(√2)
- PB=Q(√5)
- PB=Q(√10)
- PB=Q(√20)
10. 수신기 전치증폭기의 잡음지수가 F1, 이득이 G1이고, 주증폭기의 잡음지수가 F2, 이득이 G2일 때, 이 수신기의 잡음지수는?
- F=F1+(F2-1)/G1
- F=F1+F2/G2
- F=F1+F2/G1
- F=F1+(F2-1)/G2
11. 통계적으로 서로 독립인 랜덤변수 X와 Y가 있다. X의 분산은 4, Y의 분산은 3이다. Z=2X+Y이면, Z의 분산은?
- 7
- 11
- 17
- 19
12. 통과대역이 2.1[GHz]~2.5[GHz]인 이상적인 대역통과 여파기의 위상이 θ(f)=-2×10-11πf이다. 2.3[GHz] 신호가 이 여파기를 통과할 때 시간지연은?
- 2.3[ps]
- 4.6[ps]
- 10[ps]
- 20[ps]
13. 스펙트럼 확산 통신방식의 장점으로 가장 옳지 않은 것은?
- 통신 내용의 보안 유지 가능
- 전송 중 발생하는 간섭에 강함
- 통신 자원인 주파수의 공동 이용 가능
- 전송 대역폭이 좁음
14. A, B, C, D 4개의 소스 알파벳에 대하여 각각 발생 확률이 0.1, 0.3, 0.2, 0.4일 때 최소 분산 허프만(Huffman) 코드를 작성한 결과 D의 코드가 1로 되었다면 A의 코드는?
- 001
- 000
- 01
- 10
15. 신호 x(t)에 대한 설명으로 가장 옳은 것은?
- x(t+t0)는 신호 x(t)를 오른쪽으로 t0만큼 이동시킨 신호이다.
- x(at)는 상수
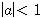 이면 시간축 상에서 확장된 신호이다.
이면 시간축 상에서 확장된 신호이다. - x(t)=x(-t)이면 기함수이다.
- x(t)≠x(t+T)이면 주기 T인 주기함수이다.
16. 무선랜(wireless LAN)에 대한 설명으로 가장 옳지 않은 것은?
- IEEE 802.11a/b/g/n 표준규격을 따르는 기술을 의미하며, Wi-Fi 용어로 사용되고 있다.
- 전송방식으로 초기에는 대역확산방식인 FH(Frequency Hopping) 방식이 이용되었다가 802.11a/g/n에서는 고속의 DS(Direct Sequence) 방식이 이용되고 있다.
- 분산제어방식으로 다른 노드가 전파를 전송하고 있는지를 확인한 후 전송하는 노드가 없는 경우 데이터를 송출하는 방식인 CSMA/CA(Carrier Sense Multiple Access / Collision Avoidance)를 사용한다.
- 무선랜 기기는 소출력으로 별도의 무선국허가 등의 관리절차가 필요 없다.
17. 슈퍼헤테로다인(superheterodyne) AM(Amplitude Modulation) 수신기에서 믹서(mixer)의 기능으로 가장 옳은 것은?
- 안테나로부터 수신한 신호를 반송파 주파수로 동조시켜 증폭한다.
- RF(Radio Frequency)단 출력과 중간주파수 차의 주파수를 발생시킨다.
- RF단의 주파수를 중간주파수 대역으로 이동시킨다.
- 중간주파수 대역의 신호만 통과시켜 증폭한다.
18. 랜덤변수 θ가 <보기>와 같은 pdf(probability density function)를 가질 때 2차모멘트(moment)는?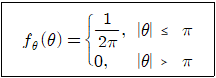
- 0
- π/2
- π2/3
- π3/4
19. 16QAM(Quadrature Amplitude Modulation)에서 심벌(symbol)들이 실수축과 허수축에 각각 -3A, -A, +A, +3A 점에 배치된다고 할 때, 두 심벌 간의 거리로 가장 옳지 않은 것은?
- 2A
- 5A
- 2√2A
- 6√2A
20. OFDM(Orthogonal Frequency Division Multiplexing)에 대한 설명으로 가장 옳은 것은?
- 데이터를 직렬로 처리하기 때문에 고속 데이터 전송이 가능하다.
- 신호를 처리하는 주기는 각 데이터 심벌 간격 T와 부반송파(sub-carrier) 수 N의 곱인 NT이다.
- 수신기에서는 IFFT(Inverse Fast Fourier Transform) 연산 후에 채널 등화기(channel equalizer)를 사용하여 심벌을 재생한다.
- 4세대 LTE(Long Term Evolution) 이동통신에서만 사용되고 있다.






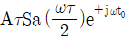
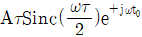
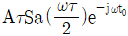
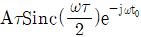
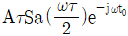 "이 옳은 답입니다.
"이 옳은 답입니다.