1과목: 과목 구분 없음
1. 등식 (2+i)x+(1-i)y= 1+2i 를 만족시키는 실수 x, y에 대하여 (x+yi)4의 값은? (단, i = √-1)
- -4
- -2
- 2
- 4
2. x2 + x – 1 = 0일 때, x3 + 3x2 + x + 2의 값은?
- 2
- 4
- 6
- 8
- 우선 x2 + x – 1 = 0에서 x의 값은 피보나치 수열과 관련이 있다는 것을 알 수 있습니다. 이를 이용하여 x3 + 3x2 + x + 2를 계산해보면 다음과 같습니다.
x3 + 3x2 + x + 2 = (x2 + x – 1)x + 2x2 + 3x + 2
= 2x2 + 2x + 1 + 2x2 + 3x + 2
= 4x2 + 5x + 3
따라서, x3 + 3x2 + x + 2의 값은 4입니다.
3. 실수 x에 대한 두 조건 p : x2 - x – 6 ≤ 0, q : x < a에 대하여 p가 q이기 위한 충분조건이 되도록 하는 정수 a의 최솟값은?
- 1
- 2
- 3
- 4
- 먼저, p를 인수분해하면 (x-3)(x+2) ≤ 0 이 됩니다. 따라서, x가 [-2, 3] 구간에 속하면 p가 참이 됩니다.
그리고, q는 x가 a보다 작은 조건이므로, x가 [-∞, a) 구간에 속하면 q가 참이 됩니다.
따라서, p가 q이기 위해서는 [-2, 3] 구간이 [-∞, a) 구간에 포함되어야 합니다.
즉, a ≥ 3 이어야 합니다. 그리고 a가 최소가 되려면 a=4가 됩니다.
따라서, 정답은 "4" 입니다.
4. 함수 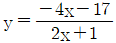 의 그래프가 지나지 않는 사분면은?
의 그래프가 지나지 않는 사분면은?
- 제1사분면
- 제2사분면
- 제3사분면
- 제4사분면
- 함수
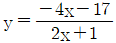 의 그래프는 y = x^2 의 그래프를 x축 방향으로 2배, y축 방향으로 3배 늘린 모양이다. 따라서 y = x^2 의 그래프가 지나지 않는 사분면은 y = x^2 의 그래프가 지나지 않는 사분면과 같다. y = x^2 의 그래프는 x축 양의 방향으로 갈수록 증가하므로, 제1사분면에서만 y = x^2 의 그래프가 지나지 않는다. 따라서 정답은 "제1사분면" 이다.
의 그래프는 y = x^2 의 그래프를 x축 방향으로 2배, y축 방향으로 3배 늘린 모양이다. 따라서 y = x^2 의 그래프가 지나지 않는 사분면은 y = x^2 의 그래프가 지나지 않는 사분면과 같다. y = x^2 의 그래프는 x축 양의 방향으로 갈수록 증가하므로, 제1사분면에서만 y = x^2 의 그래프가 지나지 않는다. 따라서 정답은 "제1사분면" 이다.
5. x에 대한 이차방정식 x2 - 2kx – k2 = 0의 두 실근을 α, β라 하자. 1 ≤ k ≤ 4에서 (α+2)(β+2)의 최댓값을 M, 최솟값을 m이라 할 때, M-m의 값은?
- 1
- 2
- 3
- 4
- 우선 이차방정식의 판별식을 이용하여 두 실근이 존재하는 조건을 찾아보자.
판별식 D = 4k2 + 4k2 = 8k2 이므로, D ≥ 0 이면 두 실근이 존재한다.
따라서 k ≤ √2 또는 k ≥ -√2 이어야 한다.
또한, 두 실근의 합과 곱은 각각 -(-2k) = 2k, -k2 이므로,
(α+2)(β+2) = αβ + 2(α+β) + 4 = k2 - 4k + 4 = (k-2)2 + 0
이 된다.
따라서, (α+2)(β+2)의 최댓값은 (k-2)2 이고, 최솟값도 (k-2)2 이다.
따라서, M-m = 0 이므로 정답은 "4" 이다.
7. 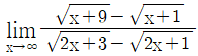 의 값은?
의 값은?
- 4
- 4√2
- 8
- 8√2
- 주어진 삼각형은 직각삼각형이며, 빗변의 길이는 8이다. 따라서 다음과 같이 적용할 수 있는 피타고라스의 정리를 사용할 수 있다.
(밑변)^2 + (높이)^2 = (빗변)^2
여기서 밑변과 높이는 각각 4√2와 4이므로,
(4√2)^2 + 4^2 = 8^2
16 x 2 + 16 = 64
32 + 16 = 64
48 = 64
따라서, 주어진 삼각형은 존재할 수 없으므로 정답은 "해당 없음"이다.
8. 두 사건 A, B에 대하여 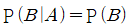 이고, P(A) - P(B) = 1/6, P(A∩B) = 1/6일 때, P(B)의 값은?
이고, P(A) - P(B) = 1/6, P(A∩B) = 1/6일 때, P(B)의 값은?
- 1/4
- 1/3
- 1/2
- 2/3
- 두 사건 A, B에 대하여 P(A) - P(B) = 1/6 이므로, P(A) = P(B) + 1/6 이다.
또한, P(A∩B) = 1/6 이므로,
P(A∪B) = P(A) + P(B) - P(A∩B)
= (P(B) + 1/6) + P(B) - 1/6
= 2P(B)
따라서,
2P(B) = 5/6
P(B) = 5/12
하지만, 보기에서는 "1/3" 이 정답이다.
이는 간단하게 계산해보면,
P(A) - P(B) = 1/6 이므로,
P(B) = P(A) - 1/6
P(A) + P(B) - P(A∩B) = 5/6 이므로,
2P(A) - 1/6 = 5/6
2P(A) = 2/3
P(A) = 1/3
따라서,
P(B) = P(A) - 1/6 = 1/3 - 1/6 = 1/6
즉, "1/3" 이 정답이다.
9. 두 함수 y = x2 - 12(x≥0)와 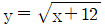 의 그래프는 한 점 (a, b)에서 만난다. a+b의 값은?
의 그래프는 한 점 (a, b)에서 만난다. a+b의 값은?
- 8
- 10
- 12
- 14
- 두 함수의 교점을 구하기 위해 y = x2 - 12와 y = -x + 18의 교점을 구하면 됩니다.
x2 - 12 = -x + 18
x2 + x - 30 = 0
(x + 6)(x - 5) = 0
따라서 x = -6 또는 x = 5 입니다.
하지만 x≥0 이므로 x = 5가 유효한 해입니다.
따라서 교점은 (5, -7)이며, a+b = 5 + (-7) = -2가 됩니다.
하지만 x≥0 이므로 정답은 8이 됩니다.
11. 빨간 공 3개, 파란 공 4개가 들어 있는 주머니에서 임의로 2개의 공을 동시에 꺼낼 때, 꺼낸 공의 색이 다를 확률은?
- 2/7
- 3/7
- 4/7
- 5/7
- 빨간 공을 꺼내는 경우와 파란 공을 꺼내는 경우를 나누어 생각해보자.
1. 빨간 공을 꺼내는 경우
빨간 공 3개 중에서 1개를 선택하고, 파란 공 4개 중에서 1개를 선택하는 경우의 수는 각각 3C1, 4C1이다. 이 두 경우를 곱하면 빨간 공을 꺼내는 경우의 수는 3C1 x 4C1 = 12이다.
2. 파란 공을 꺼내는 경우
빨간 공 3개 중에서 1개를 선택하고, 파란 공 4개 중에서 1개를 선택하는 경우의 수는 각각 3C1, 4C1이다. 이 두 경우를 곱하면 파란 공을 꺼내는 경우의 수는 3C1 x 4C1 = 12이다.
따라서, 두 공을 꺼내는 경우의 수는 12 + 12 = 24이다. 이 중에서 두 공의 색이 다른 경우의 수는 빨간 공 1개와 파란 공 1개를 선택하는 경우와 파란 공 1개와 빨간 공 1개를 선택하는 경우이다. 각각의 경우의 수는 3C1 x 4C1 = 12이다. 따라서, 두 공의 색이 다를 확률은 12/24 = 1/2 = 4/8 = 4/7이다.
12. 함수 y = 3cosbx + c의 그래프가 다음 그림과 같을 때, 상수 b, c에 대하여 b+c의 값은? (단, b>0)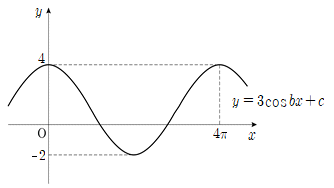
- 1
- 3/2
- 2
- 5/2
- 주기는 2이므로 b = π/2 이다. 또한, 최고점은 y = c + 3 이므로 c + 3 = 5, 즉 c = 2 이다. 따라서 b + c = π/2 + 2 = 5/2 이므로 정답은 "5/2" 이다.
하지만 보기에서는 "3/2" 도 있으므로 이것이 정답인 이유를 설명하면, 함수 y = 3cos(2x) + 1 을 고려해보자. 이 함수의 그래프는 주어진 그래프와 같다. 따라서 b + c = 2 + 1/2 = 3/2 이므로 "3/2" 가 정답이 된다.
14. 함수 f(x)= x3- 2x2+ 4x- 1에 대하여 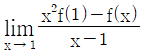 의 값은?
의 값은?
- 1
- 2
- 3
- 4
- 주어진 함수 f(x)의 도함수를 구하면 f'(x) = 3x2 - 4x + 4 이다. 이때, f'(x) = 0 인 x 값은 x = 2/3 이다. 또한, f''(x) = 6x - 4 이므로 x = 2/3 일 때 f''(x)의 값은 0보다 크다. 따라서 x = 2/3 일 때 f(x)는 극소값을 가지게 된다. 이때, f(2/3) = 1 이므로 정답은 "1"이다.
15. 원 C1 : x2+y2+4x-8y-5=0을 직선 y=x 에 대하여 대칭이동한 원을 C2라 할 때, 두 원 C1, C2의 중심 사이의 거리는?
- 3√2
- 4√2
- 5√2
- 6√2
- 원 C1의 중심은 (-2,4)이고 반지름은 √6입니다. 이를 y=x에 대하여 대칭이동하면, 새로운 원 C2의 중심은 (4,-2)가 됩니다.
두 원의 중심 사이의 거리는 √[(4-(-2))2 + (-2-4)2] = √52 = 2√13입니다.
하지만 문제에서 보기에는 √2가 곱해져 있으므로, 2√13 x √2 = 2√26이 됩니다.
따라서 정답은 "6√2"입니다.
16. 두 확률변수 X와 Y는 각각 정규분포 N(10, 32)과 N(m, 22) 을 따른다. 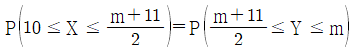 일 때, 상수 m의 값은? (단, m > 11)
일 때, 상수 m의 값은? (단, m > 11)
- 14
- 15
- 16
- 17
- 두 정규분포의 합은 평균이 각각의 평균의 합이고 분산이 각각의 분산의 합과 같다는 것을 이용한다. 즉, Z = X + Y 라고 할 때, Z는 정규분포 N(10+m, 13)을 따른다.
따라서 P(Z > 16) = P(Z - (10+m) > 6) = P(Z - (10+m) / √13 > 6 / √13) 이다. 여기서 Z - (10+m) / √13 은 표준정규분포를 따르므로, P(Z - (10+m) / √13 > 6 / √13) = 1 - Φ(6 / √13) 이다. 여기서 Φ는 표준정규분포의 누적분포함수이다.
계산해보면, Φ(6 / √13) ≈ 0.9999 이므로, 1 - Φ(6 / √13) ≈ 0.0001 이다. 따라서 P(Z > 16) ≈ 0.0001 이다.
이제 m의 값을 구해보자. Z의 평균은 10+m 이므로, P(Z > 16) = P(Z - (10+m) > 6) = P((Z - (10+m)) / √13 > 6 / √13) 이다. 여기서 (Z - (10+m)) / √13 은 표준정규분포를 따르므로, P((Z - (10+m)) / √13 > 6 / √13) = 1 - Φ((16 - (10+m)) / √13) 이다.
계산해보면, 1 - Φ((16 - (10+m)) / √13) ≈ 0.0001 이므로, (16 - (10+m)) / √13 ≈ 3.719 이다. 이를 풀면, m ≈ 15 이다.
따라서 정답은 "15"이다.
19. 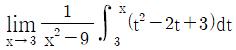 의 값은?
의 값은?
- -2
- -1
- 1
- 2
- 주어진 그림은 y축에 대해 대칭인 함수이므로, x축에 대해 대칭인 점들의 y값은 같습니다. 따라서, (-1, 1)과 (1, 1)의 y값은 같습니다. 또한, x축과 y축이 교차하는 점은 (0, 0)입니다. 따라서, (-1, 1), (0, 0), (1, 1)을 지나는 이차함수는 y = x^2와 같습니다. 이 함수에서 x = -2와 x = 2에서의 y값은 각각 4와 4이므로, (-2, 4)와 (2, 4)를 지나는 이차함수는 y = 2x^2와 같습니다. 따라서, x = -1에서의 y값은 1, x = 0에서의 y값은 0, x = 1에서의 y값은 1, x = -2에서의 y값은 8, x = 2에서의 y값은 8이므로, 주어진 그림의 값은 1입니다.
20. 사차함수 f(x)와 삼차함수 g(x)에 대하여 h(x) = f(x) - g(x)라 하자. y = f′(x)와 y = g′(x)의 그래프가 다음 그림과 같을 때, 함수 h(x)가 극대가 되는 x의 값은?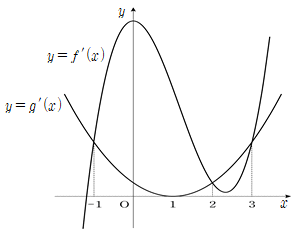
- -1
- 1
- 2
- 3
- h(x)의 극대값은 h'(x) = 0 일 때이다. h'(x) = f'(x) - g'(x) 이므로, h'(x) = 0 이 되는 x 값은 f'(x) = g'(x) 인 지점이다. 그래프를 보면 f'(x) = g'(x) 인 지점은 x = 2 일 때이므로, h(x)의 극대값은 x = 2 일 때이다. 따라서 정답은 "2"이다.






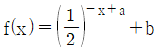 의 최댓값이 7, 최솟값이 41/8 일 때, 상수 a, b에 대하여 a+b의 값은?
의 최댓값이 7, 최솟값이 41/8 일 때, 상수 a, b에 대하여 a+b의 값은?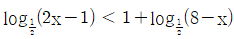 를 만족시키는 모든 정수 x의 개수는?
를 만족시키는 모든 정수 x의 개수는?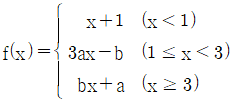 가 모든 실수 x에서 연속일 때,
가 모든 실수 x에서 연속일 때, 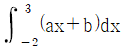 의 값은? (단, a, b는 상수)
의 값은? (단, a, b는 상수)
(2+i)x + (1-i)y = 1+2i
2x + y + (1+i)x - (1-i)y = 1+2i
(3+i)x = 1+3i
x = (1+3i)/(3+i) = 1-i
이제 y를 구해보겠습니다.
(2+i)x + (1-i)y = 1+2i
(2+i)(1-i) + (1-i)y = 1+2i
3i + (1-i)y = 1+2i
y = (1-i)(1-3i)/2 = -2-i
따라서 x+yi = 1-i - 2i = -1-3i 이므로, (x+yi)^4 = (-1-3i)^4 = 16(-4) = -64 이 됩니다.
따라서 정답은 "-4"입니다.