1과목: 과목 구분 없음
1. 금속재료는 반복하중을 받으면 정적하중을 받는 경우보다 낮은 하중으로 파괴된다. 하지만 반복하중에 의해 발생되는 반복응력이 어느 한도 이하일 경우에는 피로에 의한 파괴는 일어나지 않는다. 이 경우 측정된 편진응력의 최대값이 의미하는 것은?
- 극한강도
- 피로한도
- 탄성한도
- 크리이프한도
2. 다음 그림 (가)는 직교좌표에서 어떤 구멍의 중심위치를 치수공차로 규제한 것이고 그림 (나)는 같은 내용을 기하공차 방식으로 위치도 공차를 사용하여 규제한 것이다. 그림 (나)에서 ‘X’표시한 부분에 기재해야 하는 내용은?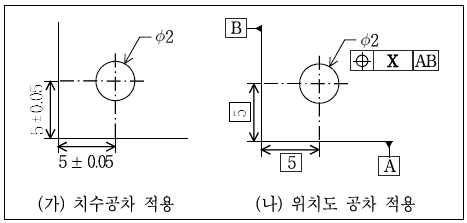
- ø0.05
- ø0.07
- ø0.10
- ø0.14
3. 다음 그림과 같이 편심하중을 받는 겹치기 리벳이음에서 가장 큰 힘이 걸리는 리벳은? (단, 도면에 기입된 치수의 단위는 mm)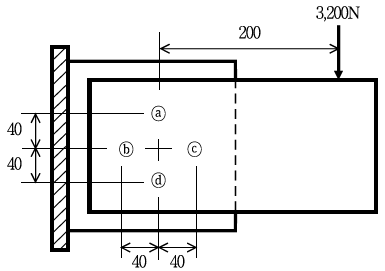
- 리벳 ⓐ
- 리벳 ⓑ
- 리벳 ⓒ
- 리벳 ⓓ
4. 회전수 600 rpm으로 20 kW의 동력을 전달하는 지름 50 mm의 회전축에 묻힘키(폭과 높이가 각각 8 mm)가 설치되어 있다. 키 재료의 허용압축응력이 25MPa일 때, 키의 길이[mm]는? (단, 키의 묻힘 깊이는 키높이의 1/2로 하고 안전율은 1로 한다)
- 32
- 48
- 64
- 128
5. 리벳이음 시공을 하지 않은 강판을 무지강판이라 한다. 단위 피치폭 무지강판의 인장강도를 A라 하고 리벳이음 시공을 한 강판에서 단위 피치폭 강판의 인장강도를 B라 할 때 B/A × 100 (%)를 강판의 효율로 정의한다. 2줄 맞대기 리벳이음에서 리벳의 피치가 100mm, 리벳지름이 20 mm, 판두께가 10 mm 일 때 강판의 효율[%]은?
- 60
- 70
- 80
- 90
6. 다음 그림은 두 축 사이에 동력을 전달하기 위한 플랜지(flange) 커플링의 개략도이다. 전달 토크가 T, 볼트의 개수가 N, 볼트의 중심 간 거리(볼트 중심을 지나는 원의 지름)가 D, 허용전단 응력이 Ta일 때 볼트의 지름 δ는? (단, 플랜지 면(面)의 마찰은 무시한다)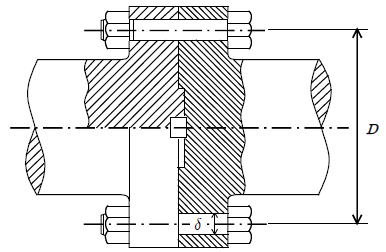
7. 기어의 ㉠모듈과 ㉡지름피치에 대한 설명 중 옳은 것은?
- ㉠: 피치원의 지름(mm)을 잇수로 나눈 값
㉡: 잇수를 피치원의 지름(inch)으로 나눈 값 - ㉠: 피치원의 지름(inch)을 잇수로 나눈 값
㉡: 잇수를 피치원의 지름(mm)으로 나눈 값 - ㉠: 잇수를 피치원의 지름(mm)으로 나눈 값
㉡: 피치원의 지름(inch)을 잇수로 나눈 값 - ㉠: 잇수를 피치원의 지름(inch)으로 나눈 값
㉡: 피치원의 지름(mm)을 잇수로 나눈 값
8. 어떤 축이 40N·mm의 비틀림 모멘트와 30N·mm의 굽힘 모멘트를 동시에 받고 있을 때, 최대주응력설에 의한 상당굽힘모멘트 [N·mm]는?
- 30
- 40
- 50
- 60
9. 마찰면의 바깥지름과 안지름이 각각 500 mm, 250 mm인 단판 원판클러치에서 축방향으로 밀어 붙이는 힘이 가해져 마찰면에 1MPa의 압력이 작용할 때 전달 가능한 최대 회전력[kN]은? (단, π=3.14, 마찰면의 마찰계수는 0.3, 마찰면의 반경방향에 대한 압력분포는 일정하다고 가정한다)
- 23.9
- 36.8
- 44.2
- 51.3
10. 압력각이 20 °인 표준 스퍼기어에서 랙(rack)과 맞물리는 피니언 (pinion)의 잇수를 설계할 때 언더컷을 방지하기 위한 이론적인 최소 잇수는? (단, sin20 °= 0.34, cos20 °=0.94, tan20 °=0.36로 한다)
- 18
- 24
- 32
- 48
11. 유니버설조인트에서 두 축간 속도비 ωB/ωA는 축이 90 °회전 할 때마다 어떻게 변화하는가? (단, 두 축의 교차각을 α라 한다)
- sinα에서 tanα 사이를 변화한다.
- cosα에서 sinα 사이를 변화한다.
- cosα에서 1/cosα 사이를 변화한다.
- sinα에서 ?/sinα 사이를 변화한다.
12. 지름이 d인 중실축(solid shaft)과 바깥지름이 d0, 안지름이 d1인 중공축(hollow shaft)이 같은 마력을 전달할 수 있다고 가정할 때 d, d0, d1에 관한 관계식 중 옳은 것은?
13. 등방성(isotropic) 재료에서 횡(세로)탄성계수(Young's modulus)를 바르게 표현한 식은? (단, G는 전단탄성계수, v는 포아송의 비)
- 2G(1-v)
- 2G(1+v)
- G(1+v)
- G(1-v)
14. 두 축이 서로 평행하고 중심선의 위치가 서로 약간 어긋났을 경우, 각속도의 변화 없이 회전동력을 전달시키려고 할 때 사용되는 커플링(coupling)은?
- 머프(muff) 커플링
- 오울드 햄(old ham) 커플링
- 유니버설(universal) 커플링
- 셀러(Seller) 커플링
15. 그림과 같이 길이 100 mm인 단순지지보의 중앙에 100 N의 집중하중이 작용할 때 보에 발생하는 최대 굽힘응력[N/mm2]은? (단, 보의 단면은 가로(밑변) 6 mm, 세로(높이) 10 mm인 사각단면이다)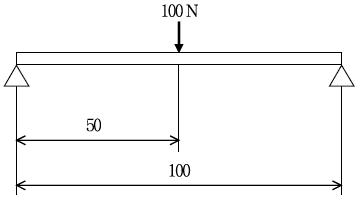
- 6
- 10
- 25
- 100
16. 용접 길이(L)가 200 mm, 판 두께(t)가 5 mm인 판을 맞대기 용접하여 그림과 같이 비이드(bead)가 형성되었다. 이 맞대기 용접부에 가할 수 있는 최대 인장하중(W) [N]은? (단, 용접부의 허용인장응력은 20 N/mm2이며 안전율은 1로 한다)
- 5000
- 10000
- 15000
- 20000
17. 벨트의 선속도가 10m/s인 상태로 10마력을 전달하는 벨트 전동 장치에서 이완측의 장력(Ts)[N]은? (단, 벨트의 회전으로 인한 원심력 효과는 무시하며 긴장측의 장력(Tt)은 이완측 장력(Ts의 두 배이다. 즉 (Tt=2Ts)
- 735
- 980
- 1470
- 1715
18. 지름이 d인 소선(황동선)을 감아 제작한 평균지름이 D인 코일 스프링이 있다. 이 코일스프링의 유효권수(소선이 감긴 수)를 동일하게 하여 지름이 d인 소선(황동선)으로 스프링의 평균지름이 2D가 되도록 제작한 것을 ‘코일스프링 갑’이라 한다. 마찬가지로 유효권수를 변경시키지 않고 지름이 2d인 소선(황동선)으로 평균지름이 D가 되도록 제작한 것을 ‘코일스프링 을’이라 한다. 여기서 ‘갑’과 ‘을’의 스프링 상수(k)에 대한 설명 중 옳은 것은?
- ‘을’과 ‘갑’이 동일하다.
- ‘을’이 ‘갑’의 8배
- ‘을’이 ‘갑’의 64배
- ‘을’이 ‘갑’의 128배
19. 내경 2000mm의 원통형 용기에 최고 압력이 1.47MPa인 가스를 저장하고자 한다. 이 압력용기 제작에 사용될 강판의 두께[mm]로 가장 적합한 것은? (단, 강판의 인장강도는 490N/mm2, 안전율은 5, 리벳이음의 효율은 70%, 부식에 대한 여유량은 1mm로 한다)
- 10
- 15
- 20
- 25
20. 초기응력이 없고, 길이방향으로 늘어나지 않도록 구속된 중실축 (solid shaft) 형상의 금속제 실린더가 있다. 이 실린더의 온도가 균일하게 상승하였을 때 발생하는 응력에 대한 설명 중 옳지 않은 것은?
- 응력의 크기는 재료의 열팽창계수에 비례한다.
- 응력의 크기는 온도 변화량에 비례한다.
- 응력의 크기는 재료의 세로탄성계수에 비례한다.
- 응력의 크기는 실린더 축방향 길이에 비례한다.






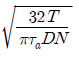
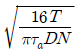
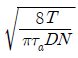
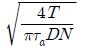
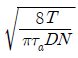 " 가 정답이 된다.
" 가 정답이 된다.
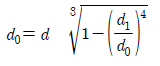
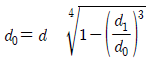

 "입니다.
"입니다.